VLW爆轰产物状态方程的发展及应用

吴 雄

(西安近代化学研究所， 陕西 西安 710065)

引 言

未来火炸药能否取得重大突破，取决于高能化合物在合成上能否取得重大进展，而高能目标化合物的正确选择有赖于爆轰参数的正确计算预报。炸药爆轰产物状态方程架起了目标化合物的微观结构与宏观性能间的桥梁，在爆轰性能参数的理论计算上尤其重要。

凝聚炸药爆轰时，在10-7秒级时间内，化学反应就达到C-J 状态，压强达数十吉帕(GPa),温度达数千度。爆轰气体产物的密度比固体炸药本身的密度还高。这种极端条件下，理想气体状态方程与范德华方程均已失去实际意义。如何建立正确描述炸药爆轰产物热力学行为的状态方程，一直是本领域科研人员的攻关目标。第一次世界大战后，人们认识到炸药爆轰产物状态方程的重要价值，多种爆轰产物状态方程应运而生，大致有以下3种模型：(1)稠密气体模型；(2)液体模型；(3)固体模型。Beckker-Kistiakowsk-Wilson方程(BKW方程)被认为是取自第三阶维里系数的稠密气体物态方程；Jacobs-Cowperthwaite-Zwisler方程(JCZ方程)是基于自由体积理论的液体模型；Jones-Wilkins-Lee方程(JWL方程)同时兼顾了固体模型和液体模型中冷能冷压贡献和分子热运动贡献。但这些经验模型都含有多个可调参数，在应用上局限性大。经验参数，尽管反复调整，但与实际应用环境也会有较大误差。为此，本研究独立自主提出VLW爆轰产物状态方程，以此抛砖引玉。该方程采用了更高阶维里方程形式，且所有系数都能从分子相互作用势参数导出，因而具有更强的理论基础和更广的适用范围。

1 维里理论方程

众所周知，由统计力学理论推导出来的维里(VIRIAL)方程，完美地解决了爆轰产物状态方程问题：

(1)

式中:B、C、D为第二、第三、第四维里系数。

(2)

(3)

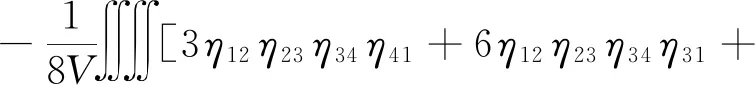
η12η23η34η13η24]dω1dω2dω3dω4

(4)

其中η12与dω1等符号的定义见文献[1]。该文献指出：“计算这些高级维里系数是很困难的， 除了用最简单的刚球模型外，计算非常麻烦。第四维里系数尚未计算出来”。文献[1]只给出了其大致猜想曲线。

这就是为什么理论完美无缺的维里方程，自1940年Mayer用统计力学理论推导出以来，至今一直没有得到实际应用的原因所在。

本研究引用维里理论，探索解决含能材料的爆轰性能参数与燃烧性能参数的计算问题。

2 背景：BKW 炸药爆轰产物状态方程

当今世界上应用最广、知名度最高的BKW炸药爆轰产物状态方程，就是从维里方程起步的[4]。

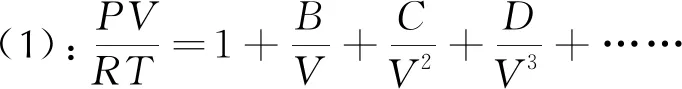
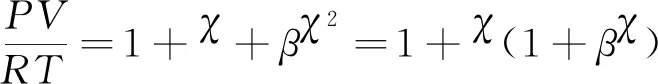
取一级近似 则有:

(5)

式(5)就是著名的 BKW 爆轰产物状态方程。

后来发现，用BKW计算的爆轰温度太低(见表1)，因此在温度T的后面增加一个经验系数θ加以调整，得到：

(6)

表1 经验系数θ与爆轰温度BKW计算值的关系(以RDX为例)

BKW 始建于20世纪20年代,经历了几代人的改进,直到20世纪50年代该方程式才确定下来。20世纪60 年代，随着计算机技术的飞速发展，通过大量炸药爆速实验数据对上述系数α、β、χ、θ拟合得到的BKW参数，对大部分炸药爆轰性能参数计算都能得到满意的计算结果，从此，世界各国纷纷引用。

20世纪70年代，我们首次将BKW状态方程及其FORTRAN BKW 程序引入国内。

众所周知，式(5)成立的必要条件为：βχ≪1，20世纪90年代笔者发现，对于某些炸药没有满足这个条件，见表2。

表2 炸药爆轰产物密度与βχ的关系

另外，将第三维里系数与第二维里系数的关系简化为：C=βB2，也缺乏坚实的理论依据。

由于BKW方程有先天缺陷，因此，它无法对各类新型炸药的爆轰性能参数都能给出合理的计算数据，20世纪70年代，经重新拟合后称为BKWR 参数；20世纪80年代，再经拟合标定后称为 BKWRR 参数。仍然无法得到满意的计算结果。

BKW状态方程建立过程中的各种标定和拟合，例如：计算温度太低，就在温度T的后面加400 还低，加1850…，均难以得到令人满意的结论。

3 VLW 炸药爆轰产物状态方程问世

统计物理指出：高温下，高级维里系数与第二维里系数之间存在某种幂函数关系。

我们试图寻找这个关系，将计算难度很大的高级维里系数均通过第二维里系数来计算解决。

文献[2] 已给出了第二、第三维里系数如下理论关系式：

B=b0B*(T*)

(7)

(8)

(9)

(10)

(11)

式中：B*(T*)、C*(T*)分别为无量纲第二、第三维里系数；N为亚佛加德罗常数；k为玻耳兹曼常数；T*为无量纲温度；σ、ε为 Lennard-Jones势参数。文献[2]只是将C(j)以表格形式给出来。

由式(8)和式(11)可知：当T*>1时，这两个级数收敛很快，当T*很大时( 爆轰条件下，T*>20)，可以只取第一项而忽略后面各项[12]，此时：

于是

(12)

式(1)可以写成：

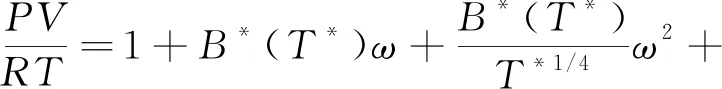
其中：

上式收敛很快，前三项在方程中起主要作用，后面诸项都是小项，对计算结果影响甚小，取前五项已足够精确。因此得到：

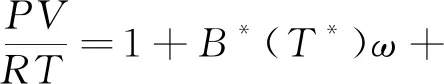
(13)

式(13)称为 VLW爆轰产物状态方程，VL代表VIRIAL理论，W代表作者吴雄(Wu)[14]。

4 应用 VLW 爆轰产物状态方程计算爆轰产物热力学函数

根据热力学理论，当选取温度T，体积V,组成Xi为独立变量，则一切热力学函数均可从自由能F推导出来。

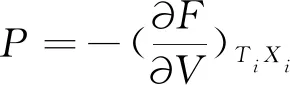
(14)

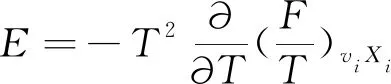
(15)

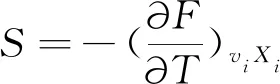
(16)

(17)

上述热力学函数未加任何限制，对任何热力学系统都是适用的，但必须有具体的状态方程表达式才能将自由能函数F确定。对于高温高压炸药爆轰产物系统，理想气体状态方程，范德华方程均已失去意义。这里采用 VLW炸药爆轰产物状态方程来确定自由能函数F。

将式(13)VLW爆轰产物状态方程写成：

(18)

(19)

则：

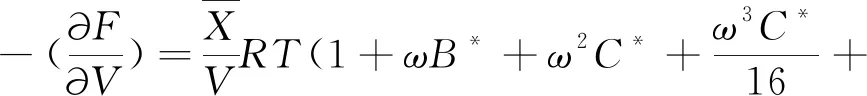
(20)

解此微分方程：

(21)

其中，

(22)

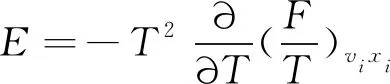
(23)

其中，

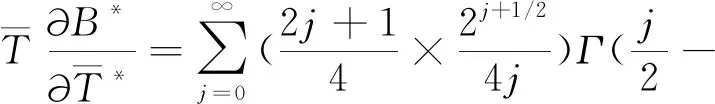
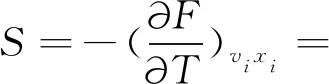
(24)

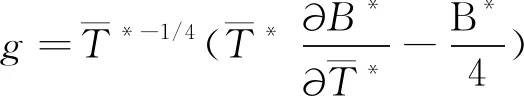
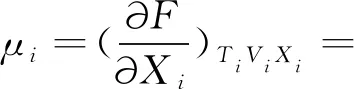
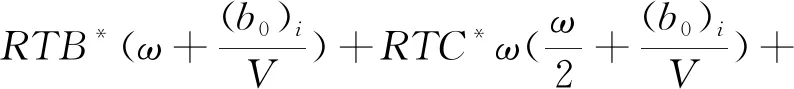
(25)

(26)

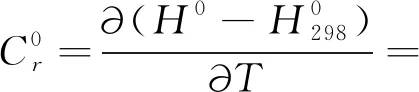
C2+2C3T+3C4T2+4C5T3

(27)

(28)

=-C1+C6T+C2T(lnT-1)+

(29)

式中：C1、C2,……C6为常数。

5 爆轰和燃烧性能参数的计算

基于VLW炸药爆轰产物状态方程、固体产物方程、爆轰理论方程组、燃烧理论方程组以及上面推导的各热力学方程，编写成为功能完善的VLW 计算机程序。本程序跨越了凝聚相爆轰与气相爆轰的传统计算鸿沟。对于初始密度，从10-3g/cm3数量级到2.0g/cm3以上都是适用的。可以计算凝聚炸药的爆轰性能参数,也可以计算燃料空气等气相炸药的爆轰性能参数，还可以计算火箭推进剂燃烧性能参数。表3～表7列出了 VLW有关计算结果，并与实验值以及 BKW计算值作了比较，表6还增加了文献[5]统计力学计算值的比较。

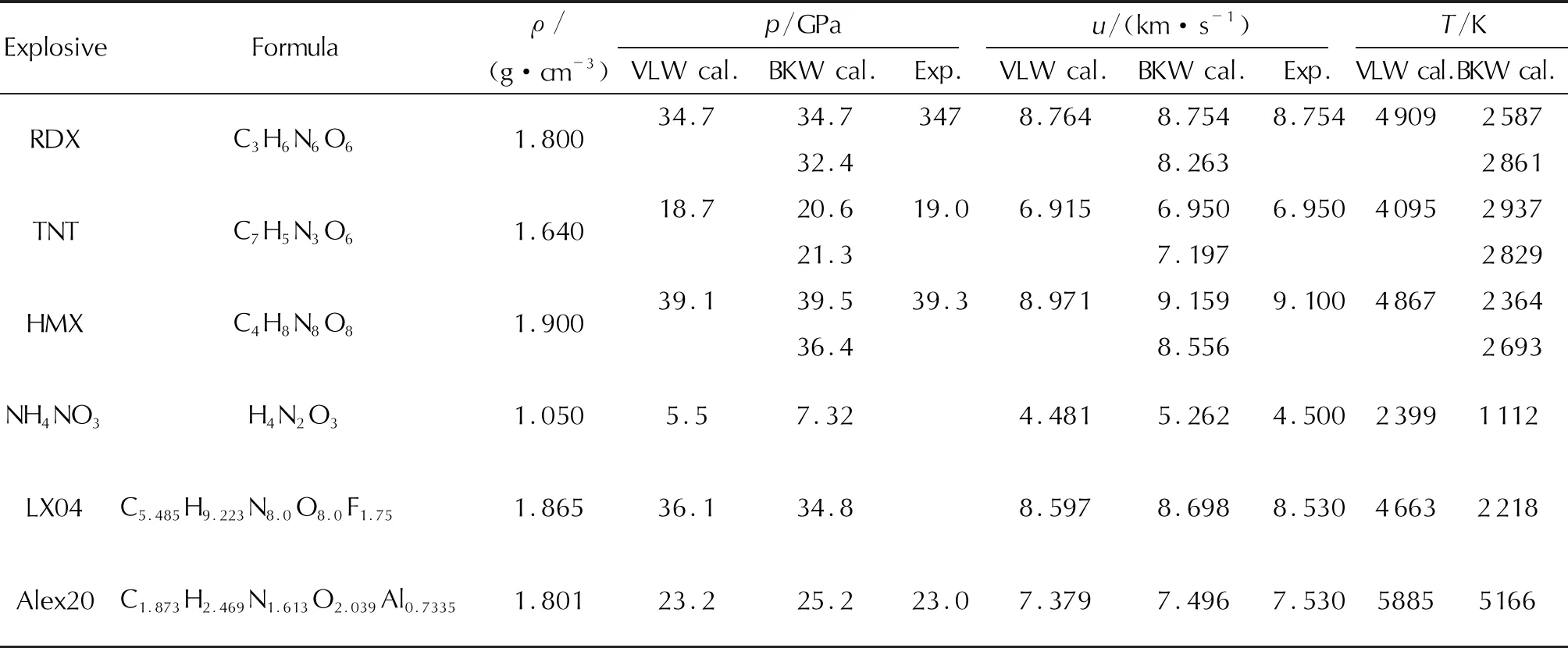
表3 凝聚炸药爆轰参数计算结果

表4 新型高能密度材料爆轰性能参数计算结果

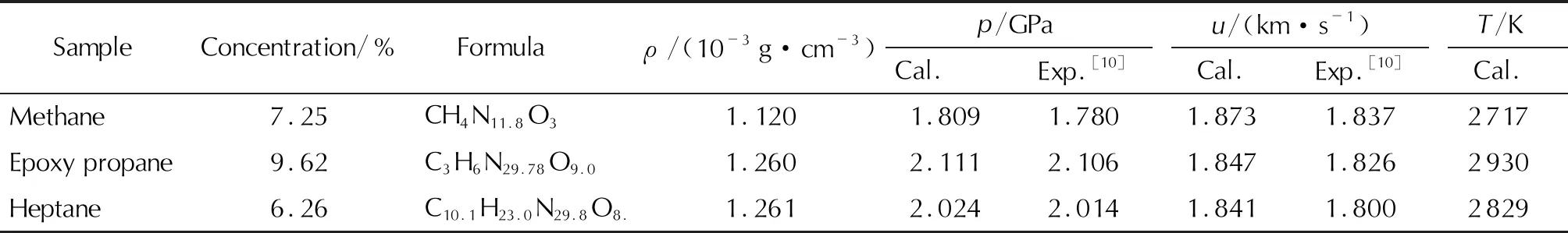
表5 燃料空气炸药爆轰性能参数计算结果

表6 凝聚炸药 RDX 各种密度下爆轰参数的VLW计算值与BKW计算值、统计力学计算值、实验值之比较

Continued

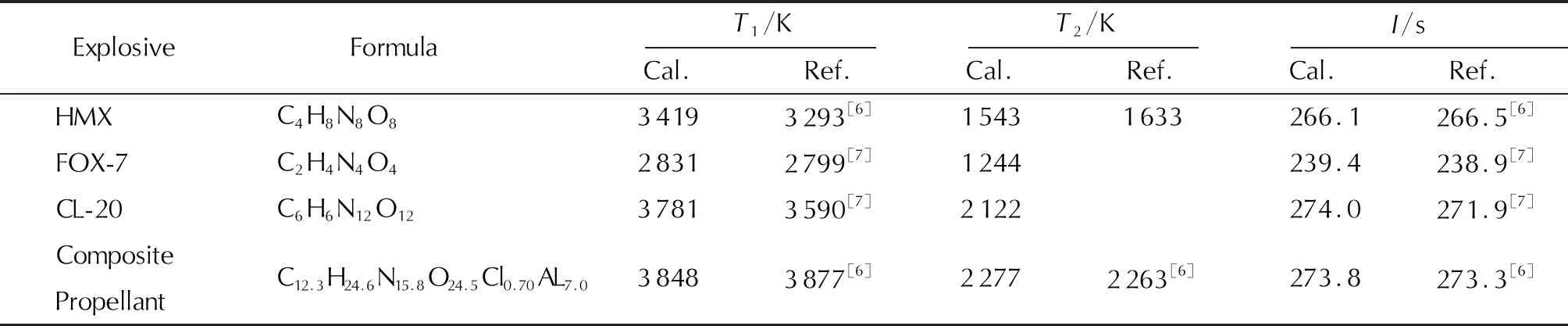
表7 火箭推进剂燃烧性能参数VLW计算值

6 结 论

解决了高温下(T*>20)高级维里系数的计算难题，以此为基础建立的VLW炸药爆轰产物状态方程,表达了高温下的维里方程属性。理论可靠，应用广泛。事实上，本方程取第一项就是理想气体方程，取前二项就是范德华方程。它跨越了传统计算鸿沟。从军用高能炸药到民用工业炸药，从凝聚相炸药到气相燃料空气炸药,从火箭推进燃烧性能参数到炸药爆轰性能参数计算都能给出合理的计算结果。自VLW药爆轰产物状态方程问世以来,得到了广泛应用， 为新型含能材料的开发提供可靠理论依据。

致谢：感谢中国工程物理研究院龙新平、何碧、蒋小华、 祝水明等老师在VLW状态方程的发展上做出了重要贡献。感谢美国Dr. Charles L. Mader 提供了BKW 资料及FORTRAN BKW计算程序。怀念已故中国工程物理研究院董海山院士生前对本工作的支持，永记铭心！