稳健回归分析在GPS高程拟合中的应用
刘 振,吴长悦
(华北理工大学 矿业工程学院,河北 唐山 063210)
GPS是随着现代卫星技术在测绘领域的普及而产生的一种空间定位技术,具有很高的测量精度,不受时间、空间地域的限制,成本较低等优点,被广泛地应用在地质工程、交通运输、测量等领域[1]。通常情况下,利用全球定位系统(GPS)得到的海拔是WGS-84下的大地高,在实际项目施工时,GPS测得的大地高是不能直接利用的,需要通过高程异常值求得海拔[2],高程的异常值是大地高与正高之间作差而得到的,对于大部分工程项目,由于施工区域面积较小,高程异常的变化比较缓慢,利用普通的多项式拟合就能够满足施工精度的需求[3]。高程拟合的实际机理就是把高程的异常值与地面坐标近似地看作一个多项式内部的关系,运用已知公共点的大地高和正常高构成误差方程,根据最小二乘法的原理(LS)求解多项式的系数。最小二乘法规定所求残差的平方和最小,它重点是针对观测过程中偶然产生的误差起作用[4]。在实际施工测量中不可避免地存在较大误差,由于传统的最小二乘法不具备抵抗较大误差的能力,所以当样本存在较大误差时,一定会对整个回归方程的系数估计构成严重影响,因抗差估计具有抵抗较大误差的特性,故本文把抗差估计引入GPS高程拟合,以达到提高精度的目的。
1 高程拟合的原理
我国在施工测量中,通常是利用正高作为高程值,地球表面上的点沿铅垂方向到与地球近似的椭球表面的长度叫作正常高Hr,在本实验中,正常高是利用二等水准得到的[5];地表上的点沿法线的方向延伸到参考椭球面的长度称为大地高H84,是利用GPS点连结成网,经过平差处理得到的以WGS-84为椭球基准面的高,这就有必要找出GPS 点的大地高H84与正常高Hr之间的关系,并将H84转换为Hr。大地高与正常高的关系如图1所示,其中,高程异常值用似大地水准面到椭球面之间的高差ξ来表示[6]。由图1可知,要求得某点的GPS正常高Hr,只需该点的高程异常值ξ和它的大地高H84。

图1 大地高与正常高的关系
Hr=H84-ξ
(1)
把水准测量和GPS测量相结合,是当前GPS施工测量中频繁使用的手段之一,当前世界上用GPS和水准相结合求得高程的主流方法为曲面拟合法[7]。
2 曲面拟合法原理
曲面拟合法作为一种多项式拟合的方法,把高程的异常值ξ近似看作因变量y,测区内的各个坐标看作自变量x,然后依据测量范围内已知的平面坐标(x,y)和ξ值组成方程组,通过解方程就可以求得函数的拟合系数,从而拟合出所测区域内的似大地水准面,再内插未知点平面坐标解得未知点的ξ,求出未知点的正常高Hr[8]。
设测站点的高程异常值ξi与坐标(xi,yi)之间存在以下函数关系:
ξi=f(xi,yi)+εi
(2)
式中,(xi,yi)为ξi的近似值;εi为拟合残差。
经过研究大量有关GPS高程拟合的相关资料,最终得到一致的结论:在所有的拟合方法中二次曲面拟合的结果精度要高于其余的拟合方法,所以本文直接利用二次曲面拟合。
二次曲面拟合方程可表述为:
ξ=a0a1x+a2y+a3x2+a4xy+a5y2
(3)
相应的误差方程为:
(4)
如果有n个水准测量点,用矩阵可表示为:
b=Aβ
(5)
式中,
b=[ξ1,ξ2,...,ξn]T
β=[a0,a1,a2,a3,a4,a5]T
由上式可知,系数矩阵A除第一列是常数项之外,其它项都是由观测值构成,所以,误差一定会存在于观测向量b和系数矩阵A之中,使用传统的最小二乘法已经不能满足需求,引入稳健回归分析[9]:
b-ε=(A-σ)β
(6)
式中,b为含随机误差ε的观测向量;A为含随机误差δ的n×m维系数矩阵;β为m维待估参数向量。
3 实验分析
3.1 数据介绍
实验数据选取华北理工大学18级研究生空间大地测量学第四和第二测量小组的静态GPS数据和二等水准数据。将11个已知点分为两组,其中8个点作为拟合点,如表1所示,进行二次曲面的多项式拟合,剩下3个作为检核点,如表2所示,用来对拟合结果精度的检核,从而判断所建立回归方程的准确性和有效性。

表1 拟合点数据/m

表2 检核点数据/m
3.2 算法流程
高程拟合的具体流程如图2所示。

图2 高程拟合流程图
3.3 在MATLAB中进行验证
3.3.1 高斯-牛顿迭代法在MATLAB中的实现
在MATLAB中,提供了nlinfit函数用于求解高斯-牛顿法的非线性最小二乘数据拟合[7]。函数的调用格式如下:

[beta,r,J,COVB,mse]=nlinfit(X,y,fun,beta0):同时返回的beta为拟合系数,r为残差,J为jacobi矩阵,COVB为评估的协方差矩阵,mse为误差的方差。输入参数beta0为初始预测值[11]。
[...]=(X,y,fun,beta0,options):指定控制参数后返回值。参数options包括MaxIter、TolFun、TolX、Display、DerivStep等。
当X为矩阵时,则X的每一列为自变量的取值,y是一个相应的列向量。如果fun中使用了@,则表示函数的句柄。
核心代码如下所示:
function F=myfunn1(beta,x)
z1=p2-q2
x=x1-mean(x1);y=y1-mean(y1);
xi=x2-mean(x2);yi=y2-mean(y2);
myfunn1=inline('beta(1)+beta(2)*x(:,1)+beta(3)*x(:,2)+beta(4)*x(:,1).*x(:,1)+beta(5)*x(:,1).*x(:,2)+beta(6)*x(:,2).*x(:,2)','beta','x');
z=p1-q1;
X=[x y];
[beta,r,J,COVB,mse]=nlinfit(X,z,myfunn1,[1 1 1 1 1 1])
zi=beta(1)+beta(2)*xi+beta(3)*yi+beta(4)*xi.*xi+beta(5)*xi.*yi+beta(6)*yi.*yi
zj=beta(1)+beta(2)*x+beta(3)*y+beta(4)*x.*x+beta(5)*x.*y+beta(6)*y.*y
z2=[z1-zi]
z3=z-zj
K=z3'*z3
V=z2'*z2
N=sqrt(K/7)
M=sqrt(V/2)
3.3.2 抗差估计在MATLAB中的实现
可以利用MATLAB中已有的robustfit函数来做抗差估计[12],一般使用方式为:
B=robustfit(X,y),输入参数X是已知点坐标所组成的设定好的矩阵,它是一个n*p的矩阵,输入参数y为已知点的高程异常值所组成的矩阵,是一个n*1的列向量[13],通常采用如下调用格式:
[b,statas]=robustfit(X,y,wfun,tune):用参数wfun指定加权函数,用参数tune指定调节常数[14]。
核心代码如下:
x=x1-mean(x1);y=y1-mean(y1);% 数据中心化
xi=x2-mean(x2);yi=y2-mean(y2);% 数据中心化
z=p1-q1; % 已知点高程异常矩阵
X=[x y x.*x x.*y y.*y];
[b stats]=robustfit(X,z)
B=[1 1 1 1 1 1 1 1]'
C=horzcat(B,X)
z2=C*b
z3=z-z2%拟合残差
D=[1 1 1]'
E=[xi yi xi.*xi xi.*yi yi.*yi]
X1=horzcat(D,E)
z4=X1*b
z5=z1-z4%检核残差
subplot(2,1,2);plot(z5,'g')
ylabel('残差(m)')
title('图(b)检核点残差图')
grid on;
subplot(2,1,1);plot(z3,'g')
xlabel('点')
ylabel('残差(m)')
title('图(a)拟合点残差图')
grid on;
N=sqrt((z3'*z3)/7)
M=sqrt((z5'*z5)/2)
3.4 实验结果及精度评定
通过MATLAB程序的运行可以得到残差图,如图3、图4所示。
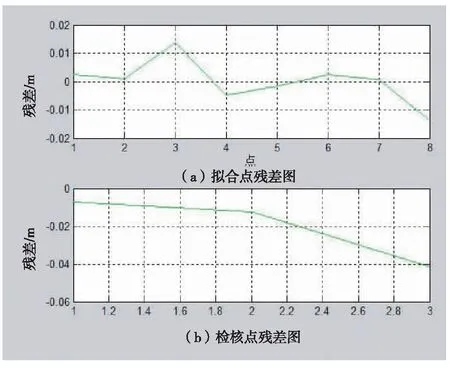
图3 高斯-牛顿迭代法得到的残差图

图4 稳健回归分析得到的残差图
实验结果如表3所示。A0~A5是拟合得到的二次曲面的系数。为了更好的进行精度评定,表中列出两种方法的拟合点和检核点的最大最小残差来进行对比,并引入内外符合精度作为评价拟合效果的指标。

表3 实验结果
3.5 实验结果分析
从残差图来看,高斯-牛顿迭代法与稳健回归分析法的拟合点残差都有波动,但波动范围较小,最大残差均不超过1.5 cm,检核点残差均不超过5 cm,但稳健回归分析的最大残差相对较小,不超过3 cm,高斯-牛顿迭代法的最大残差已经超过4 cm。由表3可知,用高斯-牛顿迭代法进行二次曲面拟合与用稳健回归分析拟合法对比如下:拟合系数差异较大,前者A0是-354.220 465,后者A0是0;拟合点的残差总体相差不大;检核点的残差,用稳健回归分析的最大残差和最小残差都相对较小;内符合精度相差不大;外符合精度稳健回归数值是0.021 1,相对较小,说明精度较高。稳健回归相比高斯-牛顿迭代法在高程拟合方面误差相对较小,具有一定的优势,也在一定程度上说明稳健回归分析用于高程拟合的现实可行性。
4 结论与不足
本文采用高斯-牛顿迭代最小二乘法与稳健回归分析法进行高程拟合,通过精度检验和对比分析,不仅说明在地势比较平坦的地区用GPS水准进行高程拟合基本可以满足精度要求,还证明了在观测数据存在粗差的情况下,用稳健回归能够在一定程度上提高拟合精度,具有现实可行性。但是由于条件的限制,实验数据量较少,高程拟合的测区范围也不大,实验结果存在一定的局限性,可以通过大区域和更多的数据来进行更深入的研究。

