基于距离较差法控制点稳定性分析

李秉乾，邸国辉，褚成凤，郭际明，万年锋

（1.湖北省水利水电规划勘测设计院，湖北 武汉 430064；2.武汉大学测绘学院，湖北 武汉 430079）

鄂北地区水资源配置工程是为解决鄂北地区干旱缺水问题的一项大型水资源配置工程，由于工程建设周期较长，施工区域条件复杂，GNSS 控制网容易发生点位移动，需要定期复测控制点，以判断其是否稳定。

常用的控制点单点稳定性分析方法有坐标较差法、距离较差法、统计检验法、变形误差椭圆法[1]。在已有的方法中，没有考虑同一个控制点坐标分量的协方差以及不同控制点之间的协方差[2-7]。本文在三维无约束平差的基础上，顾及控制点坐标分量间方差和协方差进行分析计算，进而对控制点进行稳定性分析。

1 固定一点一方向平差

GNSS 网的约束平差中所采用的观测量为GNSS基线向量，同时引入了会使GNSS 网的尺度和方位发生变化的外部起算数据。引入边长、方向或两个及两个以上的起算点坐标，可能会使GNSS 控制网的尺度或方位发生变化。GNSS 网的约束平差常被用于实现GNSS 控制网由基线解算时所用的特定参考系的转换。

固定一点一方向平差，即在二维投影面上，引入一个起算点的坐标和一条基线的方位角，进行约束平差。采用两期观测的同名基线求差，根据相对中误差最小准则，确定平差基准。GNSS 三维基线向量在WGS-84 坐标系下经三维无约束平差后，将GNSS 点的三维坐标投影到工程椭球所对应高斯平面上。设地面固定点在独立坐标系下的平面坐标为(x0′ ,y0′)，此点对应高斯投影后的平面坐标为(x0,y0)，特定方向方位角为α0′1，其对应由高斯投影后平面坐标反算的方位角为α01，那么各GNSS 点在独立坐标系下的平面坐标为：

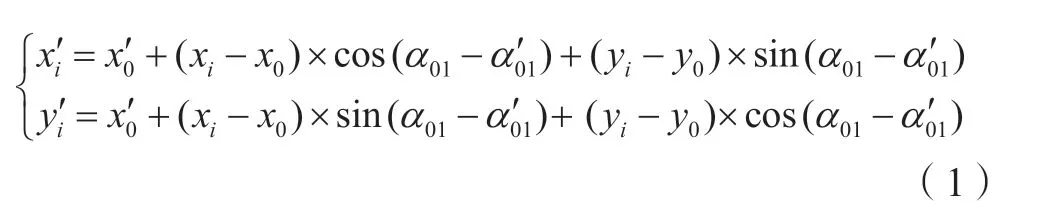
式中，xi′、yi′为GNSS 点在独立坐标系中的平面坐标；xi、yi为三维无约束平差后转换得到的工程椭球所对应高斯平面直角坐标。上式即为工程GNSS 网固定一点一方向平差的函数模型。

由协方差传播定律可知，将WGS84 空间直角坐标系下的GNSS 三维基线向量协方差阵的随机信息传递到工程独立平面坐标系的过程如下：

1）经三维无约束平差后，将GNSS 三维基线向量的协方差矩阵DΔXΔYΔZ转化为大地坐标的协方差矩阵DBLH；

2）经高斯正算得到各GNSS 点在工程椭球所对应的高斯平面坐标，大地坐标的协方差矩阵DBLH也转化为高斯平面坐标的协方差矩阵Dxy；

3）高斯平面坐标向工程独立坐标转换，得到工程独立坐标系下坐标的协方差矩阵Dxy′ ；

4）工程独立坐标系下，坐标的协方差矩阵Dxy′ 转换为独立坐标系下二维基线向量的协方差矩阵DΔ′xΔy。

综上，独立平面坐标系下二维基线向量的协方差的获得过程即为：DΔXΔYΔZ→ DBLH→ Dxy→ Dx′y→ DΔ′xΔy，则有：

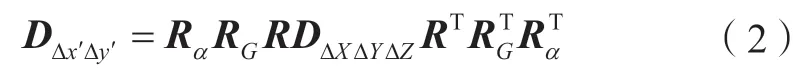
式中，Ra、RG、R 分别为大地坐标转换、高斯投影、平面坐标转换对应的参数矩阵。在独立坐标系下，GNSS 二维基线向量参与最小二乘平差，其随机模型DΔxΔ′y′也同时按照协方差传播定律来进行变换，并由此可对GNSS网一点一方向平差结果的精度进行评定。

2 距离较差法

2.1 经典的距离较差法

对于某一平差网中的2 个控制点A、B，假设A点是稳定点，B 点为待定点，两期边长观测值之差：，ΔSAB的中误差为：实际测量中常以仪器标称精度mD为中误差，即：mD=a+b×S，其中a 为固定误差，b 为比例误差，S为基线长度。

该方法适用于控制点单点稳定性分析。

2.2 平面方向稳定性分析新方法

对于某一平差网中的2 个控制点A、B，其坐标分别为（XA,YA）和（XB,YB），这2 个控制点之间的方差协方差矩阵为：

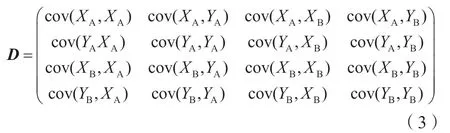
此处控制点的协方差矩阵由COSAGPS 定制版软件输出，具体实现如下：

用户自定义输入点对信息文件：

文件名称：项目名.GNSS2dPointPairInFile1

文件结构：每行输入一对点，以空格分隔。

进行固定一点一方向平差，得到输入点对应的两个点的坐标的方差-协方差输出结果文件：

文件名称：项目名.GNSS2dPointPairCovOutFile1

文件结构：一对点的名称占一行，后续4 行是这2 点对应的4×4 的方差协方差矩阵（单位：mm）。

控制点A、B 之间的距离如下：

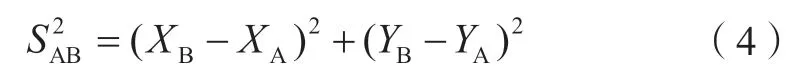
对函数式求全微分得：

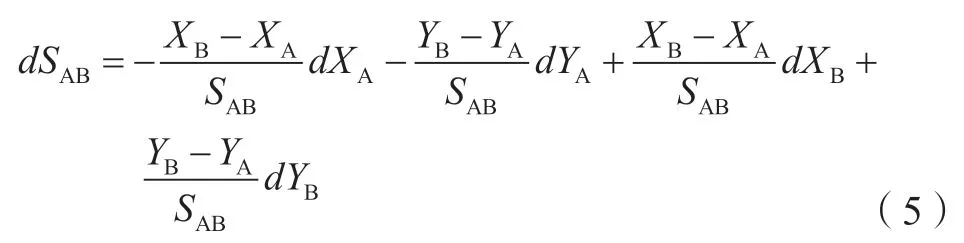
将微分关系式写成矩阵形式：dSAB=KdL

其中，

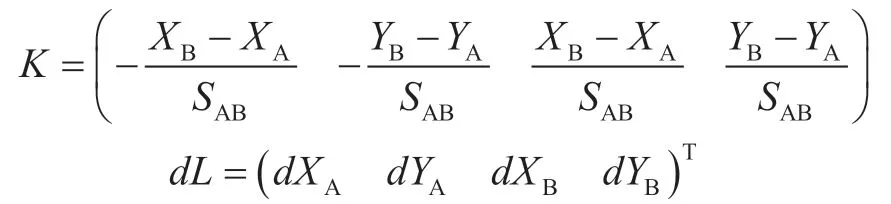
应用协方差传播律，即可求得：

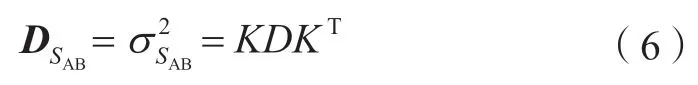
当A 为固定一点一方向平差中的固定点时，与A 相关的方差协方差均为零，此时上式可化简为：

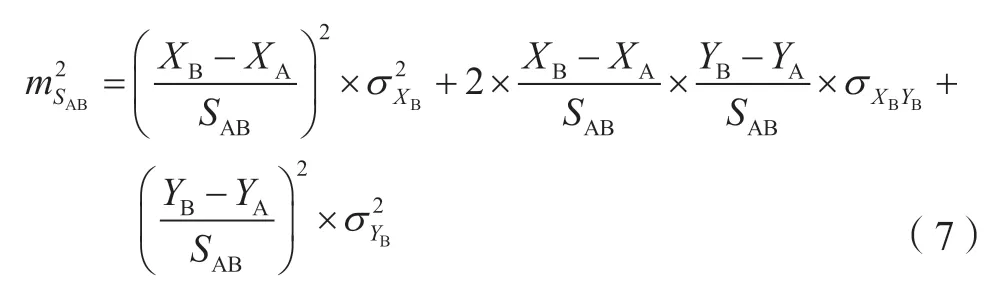
式中，σXYBB为控制点B 的X、Y 坐标分量之间的协方差。

对于GNSS 控制网中的两个同名控制点A、B，其第一期观测平差后坐标为和，这2 个控制点之间的方差协方差矩阵为：

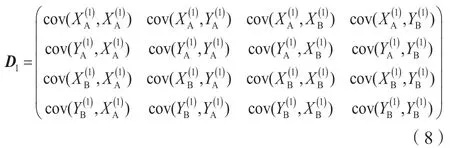
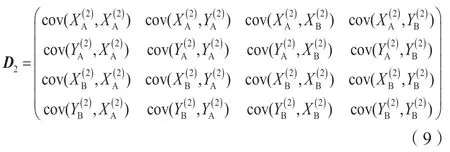
因此有第一期观测得到的AB 边的方差：

式中，

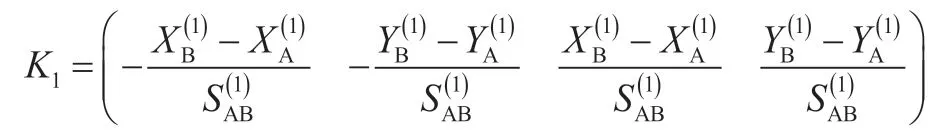
第二期观测得到AB 边的方差：

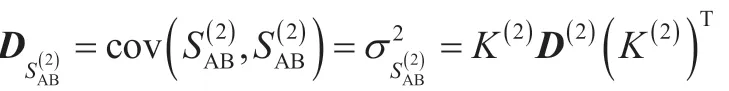
式中，

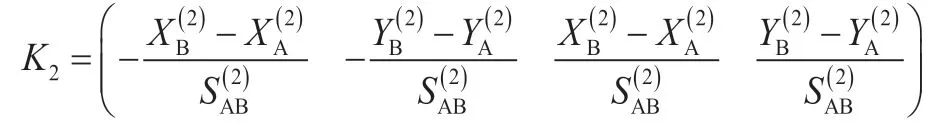
两期观测的边长观测值之差：

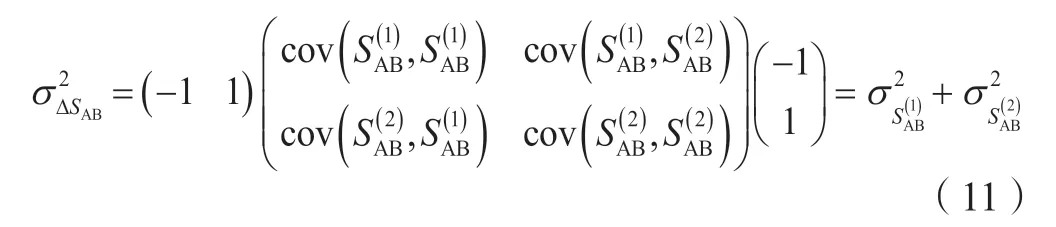
3 具体算例

鄂北地区水资源配置工程的某段带状控制网，长度约16 km，建网于2015 年12 月间观测了67 个控制点；2016 年复测了65 个控制点，其中58 个控制点是建网时观测的控制点，7 个控制点为新增观测点。

对于控制点在平面方向上的稳定性，此处利用整个广水段的58 个同名控制点进行研究。采用两期观测的同名基线求差，根据相对中误差最小准则，以3 550 点作为固定点，基线3 550-129 的方向作为固定方向，对GNSS 卫星观测的基线数据进行固定一点一方向平差，得到2016 年观测控制点的坐标和2015 年建网观测坐标。

计算两期基线之差，分别采用同时顾及方差和协方差的全协方差阵法、只考虑方差的距离较差法和经典的距离较差法对控制点的点位位移作稳定性分析，经典的距离较差法的基线中误差为5 mm+1 ppm，不同距离较差法的△S 中误差见图1，距离较差法的稳定性分析结果见表1。

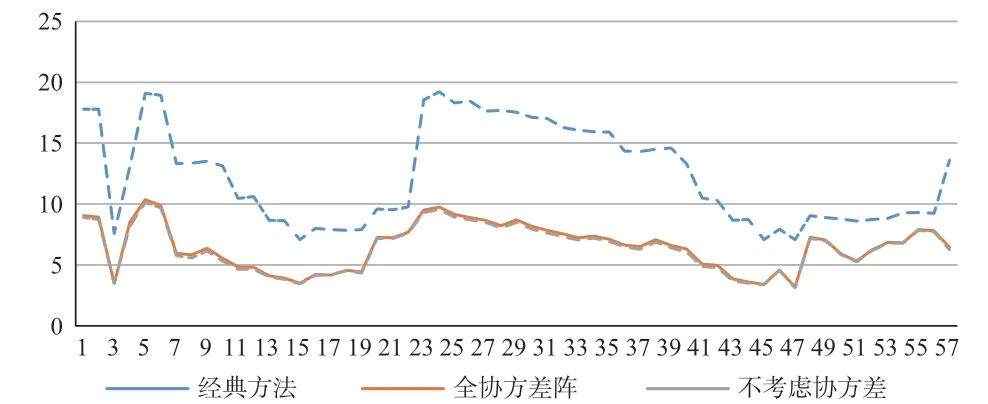
图1 不同距离较差法的△S 中误差分布图

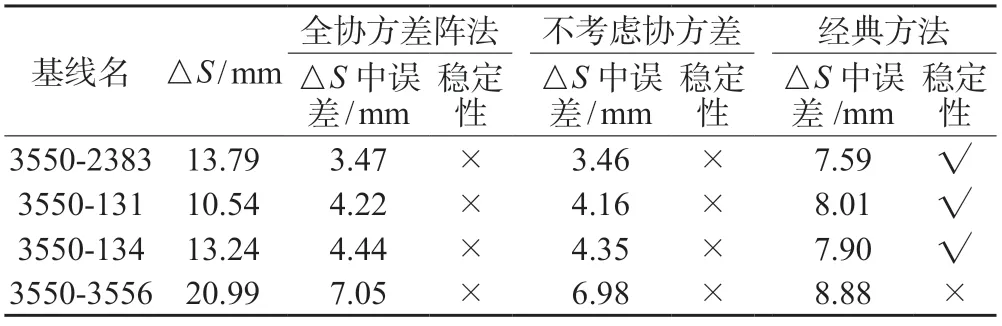
表1 距离较差法的稳定性分析结果

基于全协方差新方法和不考虑协方差的方法计算得到的△S 中误差相差不多，不稳定点均为2 383、131、134 和3 556。用经典的距离较差法与基于全协方差新方法得到的△S 中误差相差90%，不稳定点仅有3 556。

4 结 语

本文对鄂北地区水资源配置工程的某段带状控制网两期观测的GNSS 数据进行解算，并利用COSAGPS软件进行固定一点一方向平差，根据两期平差结果对同名控制点的稳定性进行分析，结果表明控制网中控制点2383、131、134 和3556 不稳定，其他点稳定。

针对基于协方差阵、不考虑协方差的距离较差法与经典方法对比，发现前2 种方法得到的中误差、限差相差不大，但均明显小于经典方法，基于全协方差阵的距离较差法可以减小将不稳定点误判为稳定点的可能性。