真三轴应力下混凝土的动态力学性能及破坏准则

徐媛媛 ，彭 刚 ，王乾峰 ，肖姝娈 ，李 威 ，彭竹君

(1. 防灾减灾湖北省重点实验室（三峡大学），湖北 宜昌 443002；2. 三峡大学 土木与建筑学院，湖北 宜昌 443002)

混凝土结构在实际工程应用中除了承受静态荷载作用外，还要遭受地震、冲击和爆破等动态荷载的作用，且在动态荷载作用下表现出区别于静态荷载作用下的力学性能。因此，研究混凝土的动力特性对评价混凝土结构的安全性和稳定性十分重要。目前，国内外学者关于混凝土材料的动态力学特性研究主要集中于单轴和双轴应力状态[1-7]。混凝土在多轴应力状态下的动态特性研究也取得一些进展，如尚世明等[8-9]进行了恒定围压下的混凝土动态三轴压缩试验，试验结果表明混凝土的三轴抗压强度随围压和应变速率的增大而增大，峰值应变随应变速率的变化规律有所不同。田为和彭刚等[10-12]开展了水环境下的混凝土动态常三轴试验，发现围压的存在会提高混凝土的强度及其对应变速率的敏感性。施林林等[13]研究了大骨料混凝土经历动态三轴压荷载历史后的单轴抗压强度和损伤特性。宋玉普等[14-16]研究了应力比对三轴压和三轴拉压压应力状态下混凝土动态强度的影响，试验表明应力比在1.0∶0.5∶0.1附近时三轴抗压强度最大，并建立了动态破坏准则。

综上可知，有关混凝土在多轴应力状态下的动态试验研究中，由于试验设备和技术操作的复杂性，开展的常规三轴试验较多、真三轴试验甚少，针对混凝土强度特性的研究较多、变形特性的研究甚少，并且试验结果受到试验操作和环境等因素的影响，导致所得出的结论也有所差别。因此，有必要进一步开展混凝土在动态荷载下的三轴试验研究，深入探讨复杂应力状态下混凝土的动态力学性能，丰富此方面研究成果，为构建混凝土的动态本构模型以及结构设计提供理论依据。本文拟开展不同应力比和不同加载速率下的混凝土真三轴静、动态试验，获得较为完整的应力-应变关系曲线，分析混凝土的强度和变形特性，并基于八面体应力空间准则，建立考虑应变速率效应影响的动态破坏准则。

1 试验设计

混凝土设计强度为C30，根据《普通混凝土配合比设计规程》（JGJ 55—2011）[17]进行质量配合比设计，即m(水)∶m(水泥)∶m(砂)∶m(石子)=0.50∶1.00∶2.04∶3.96。水泥采用P·O 32.5普通硅酸盐水泥；拌合水为饮用自来水；粗骨料粒径为5～40 mm的连续级配碎石；细骨料为连续级配天然河沙，经筛分后实测细度模数为2.3，属于中砂。每立方米混凝土各组成材料用量分别为水81.0 kg/m3，水泥162.0 kg/m3，砂330.5 kg/m3，石子640.9 kg/m3。

本试验所用的混凝土试件尺寸为150 mm×150 mm×150 mm的立方体，混凝土试件在塑料模具中浇筑成型，在振动台上振捣密实，室内放置24 h后拆模，然后放入标准养护室（相对湿度为95%以上，温度为(20±2)℃）中养护28 d。试验时，混凝土试件的龄期已达到90 d，其单轴抗压强度为36.65 MPa。

本次试验采用10 MN微机控制电液压伺服大型多功能动静力三轴仪，该设备可进行常三轴和真三轴混凝土动静力加载试验。试验过程如下：

（1）装样：在试件表面粘贴减摩垫片进行减摩处理，减摩垫片为涂抹了少量均匀黄油的两片铝片叠成。将试件安装在三轴试验机的加载板中心，使之保持在三轴仪3个方向的荷载传感器的中心。

（2）预加载：为保证试件与荷载传感器能够充分接触，先进行竖向（对应的应力方向为 σ3向）预加载，再施加两个水平方向（对应的应力方向为σ1和 σ2向）预荷载，3个方向设定的预加荷载都为15 kN。

（3）正式加载：用荷载控制方式（1 000 N/s）对试件的两个水平方向同时施加压应力至设计的应力比（σ2∶σ1=1∶1、2∶1、3∶1、4∶1）并保持恒定，然后在 σ3向利用变形控制方式分别进行不同应变速率（10−5/s、10−4/s、10−3/s、10−2/s）的竖向加载，加载至试件完全被破坏。

（4）卸载及后续处理：当得到完整的荷载-位移曲线后，停止加载，开始卸荷，卸荷完成后，保存试验数据。

2 强度特性分析

试验测得混凝土在不同应力比和不同加载速率下真三轴受压混凝土的极限抗压强度（见表1），极限抗压强度为加载方向（ σ3）作用在混凝土试件面上的最大应力值。由表1可知，与单轴受压相比，处于真三轴受压下混凝土的极限抗压强度显著提高，且随应变速率和应力比的增大总体上呈增大趋势。

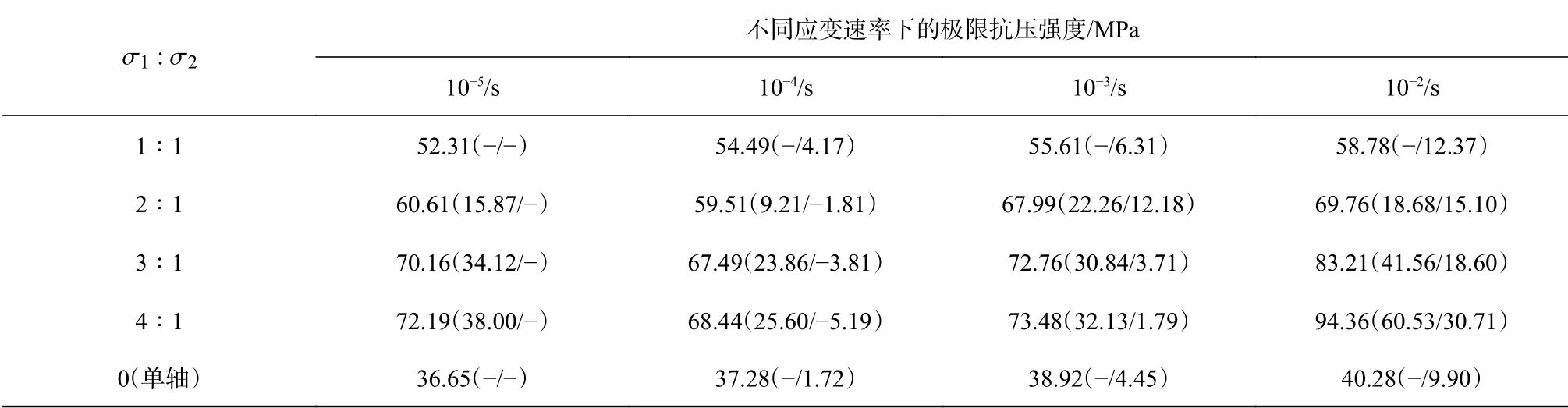
表 1 不同应变速率下混凝土的动态抗压强度Tab. 1 Dynamic compressive strengths of concrete at different strain rates

2.1 应变速率对极限抗压强度的影响

由表1可知，当应力比较低（σ2/σ1=0、1∶1）时，极限抗压强度随着应变速率的增大逐渐增大；当应力比较高（2∶1～4∶1）时，极限抗压强度随应变速率的增大先减小再增加。分析认为，从施加侧应力至达到预定应力比的过程中，侧应力会对混凝土内部造成一定程度的损伤，表现为对强度的劣化作用；当应力比达到预定设计值后再进行正式的竖向加载过程，侧应力的存在表现为对强度的增益作用。譬如，当应力比大于2∶1时，混凝土在较低应变速率（10−4/s）下，应变速率对混凝土强度的增益作用小于其侧压力的存在对混凝土强度的劣化效应，故导致混凝土强度的降低；在较高应变速率（10−3/s、10−2/s）下，应变速率对混凝土强度的增益作用大大加强，表现出混凝土强度的提高。

2.2 应力比对极限抗压强度的影响

由表1可知，在相同应变速率加载条件下，混凝土的极限抗压强度随应力比的增大而增大，并且其增加的幅度不同。当应力比小于3∶1时，极限抗压强度随应力比增大的增幅明显；应力比大于3∶1后，极限抗压强度增幅不大。如应变速率为10−4/s时，与应力比为1∶1条件下的极限抗压强度相比，应力比为2∶1、3∶1和4∶1时的极限抗压强度分别增加了9.21%、23.86%和25.60%。分析其原因是侧应力限制了混凝土的横向变形，随着应力比的增大，混凝土材料内部更加密实，使混凝土的极限抗压强度大幅提高。而当侧应力增大到一定程度时，混凝土的密实度逐渐接近其临界值，此时侧应力的增加对极限抗压强度提高的幅度影响较小，故当应力比超过3∶1时，极限抗压强度随应力比的增加，其增幅不大。

3 变形特性分析

3.1 轴向应力-应变关系曲线特征

由于试验设备的限制，早期开展的混凝土真三轴动态压缩试验大多只能得到曲线的上升段[14-16]，下降段难以被采集，本文获得了较为完整的轴向应力-应变曲线。试验实测动态荷载作用下部分典型的轴向应力-应变关系曲线见图1。由图1可知，随着应变速率的增加，曲线的峰值部位变得平缓，不同于单轴压缩下有明显的峰值点。当应力比较大（σ2∶σ1=4∶1）时，曲线的下降段在高应变速率下（10−2/s）表现出明显的平台流塑现象；在低应变速率（10−5/s）下表现出脆性，见图1（d），表明混凝土随应变速率增加而逐渐从脆性状态过渡为塑性状态。

由图1还可得，随着应力比的增大，混凝土在极限抗压强度处对应的轴向峰值应变总体上呈增大趋势。随着应变速率的增大，轴向峰值应变的变化规律在各应力比下有所不同：如图1（a）所示，当混凝土侧向所受的应力相等（σ2∶σ1=1∶1）时，其轴向峰值应变随着应变速率的增大而整体呈减小趋势，该结论与文献[9]中混凝土在动态常三轴试验所取得的结论相一致。在较高的应力比（σ2∶σ1=4∶1）下，混凝土的轴向峰值应变随应变速率的增大呈先减小后增加的变化规律。

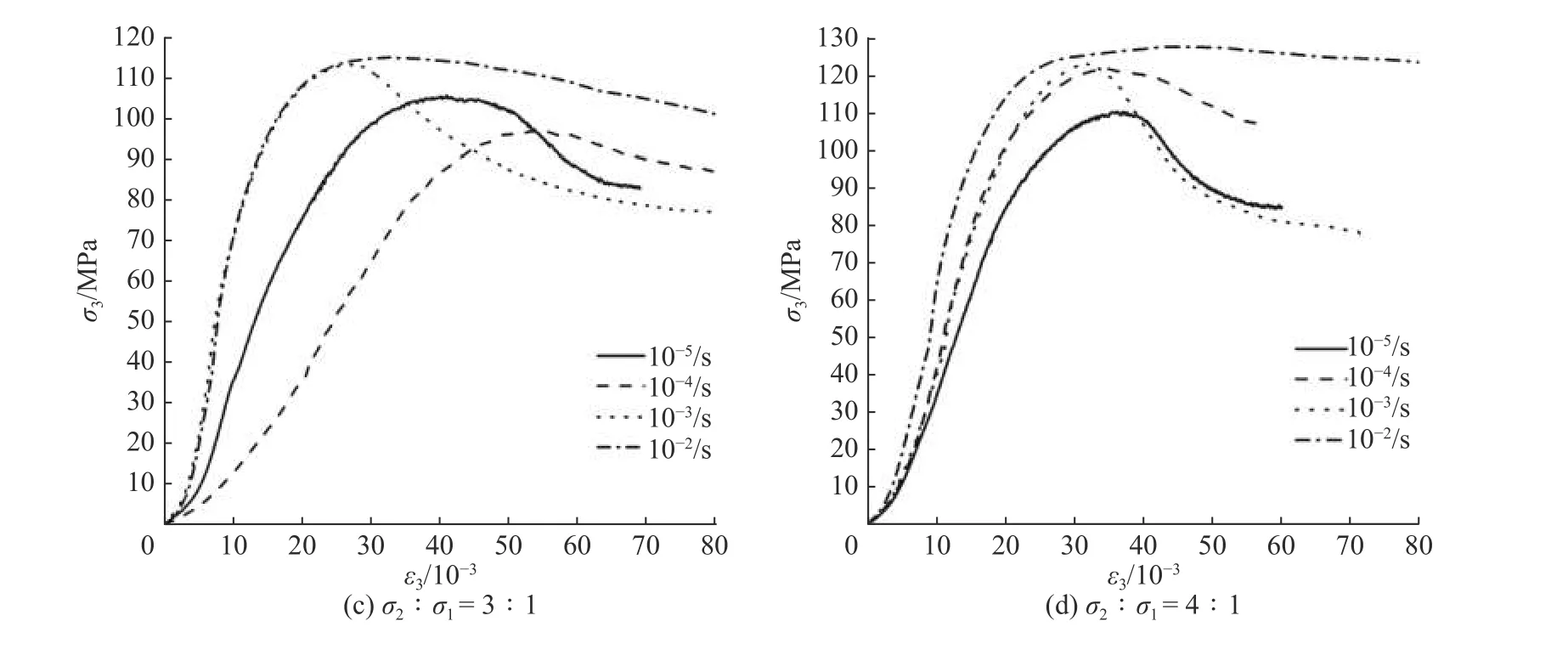
图 1 不同应变速率下混凝土的轴向应力-应变曲线Fig. 1 Axial stress-strain curves of concrete at different strain rates

3.2 侧向受压面变形特征

3.2.1 不同应变速率影响下的侧向变形 由于混凝土在不同应力比下的侧向变形随着应变速率变化的变化规律大致相同，故本文选取应力比σ2∶σ1为1∶1时的工况研究应变速率对混凝土侧向变形的影响。图2为不同应变速率加载时，混凝土在变形破坏过程中的侧向变形与轴向极限抗压强度σ3之间的变化规律。图2中，应变正值表示为压应变，应变负值表示为拉应变。

图 2 相同应力比下受应变速率影响的侧向应变（应力比σ2∶σ1=1∶1）Fig. 2 Effect of strain rate on lateral strain （σ2∶σ1=1∶1）

由图2可见，混凝土在达到其轴向极限抗压强度之前，不同应变速率下的侧向变形曲线整体呈陡直上升的变化趋势，并且侧向的变形量较小，轴向极限抗压强度处对应的应变值随应变速率的增大其规律变化不明显。另外，观察图2可以发现，与准静态加载速率（10−5/s）相比，动态荷载作用下混凝土的侧向变形曲线的破坏峰值点更加突出，随着应变速率的提高，曲线在轴向抗压强度峰值后下降趋势也更加明显，这表明混凝土随应变速率的增加表现出更明显的脆性特征。

3.2.2 不同应力比影响下的侧向变形 混凝土侧向受压面的变形与轴向极限抗压强度σ3之间的变化规律见图3。当应力比σ2∶σ1为1∶1时，侧向的变形情况大致相同。随着应力比的增大，第二主应力方向上的变形越来越小，且应力比σ2∶σ1达到4∶1时，第二主应力方向上的变形在主应力σ2达到一定值时不再变化。主要原因是，混凝土两个侧面的应力相等时，对于各向异性材料，其变形应相同，观察图3（a）表明本研究试验的变形量具有较好的精度和可靠性；当应力比增加时，侧向应力较大的面将更强地约束混凝土的横向变形，使第二主应力方向的应变较小。

图 3 应力比对侧向应变的影响Fig. 3 Effect of stress ratio on lateral strain

4 真三轴应力条件下动静态破坏准则

4.1 基于八面体应力空间的真三轴静态破坏准则

根据Bresler-Pister在八面体应力空间提出的三参数破坏准则[18]，对本文试验数据进行验证，该破坏准则的破坏包络面趋于一个二次曲面，曲面光滑且形状外凸，其模型表达式如下：

式中：fc为 单轴静态抗压强度值，本试验测得为36.65 MPa；α、β、γ为参数，共同决定破坏子午面的形状和大小； σoct为 八面体上的正应力；τoct为 八面体上的剪应力。其中，八面体上的正应力σoct和 剪应力 τoct与主应力（σ1、σ2、σ3）的变换关系按下式计算：

式中：σ1为 最大主应力；σ2为 中间主应力；σ3为最小主应力。

根据式（2）～（3）对本文试验数据进行相关计算，得到真三轴静态（10−5/s）荷载作用下的普通混凝土在八面体应力空间上的剪应力、正应力。利用式（1）对计算出的数据进行最小二乘法回归分析，得到回归系数α=−0.308， β=−1.154，γ =0.084，其对应的相关系数R2为0.96。则真三轴静态压缩状态下普通混凝土的八面体应力空间破坏准则表达式为：

八面体应力空间下的普通混凝土在不同应力比下的真三轴静态破坏准则模型与试验数据的对比见图4。图4所示的压子午面表达了八面体应力空间的普通混凝土在不同应力比条件下的破坏包络面，可以得出，强度准则曲线光滑外凸且连续，压子午线上八面体剪应力值随八面体正应力值的减小而增大，且斜率逐渐减小，有极限值点。由图4可见，建立的真三轴静态破坏准则模型与试验数据吻合较好。

图 4 八面体应力空间的真三轴静态破坏准则模型与试验数据的对比Fig. 4 Comparison of true triaxial static failure criterion model test data based on octahedral stress space and experimental data

4.2 考虑应变速率效应的真三轴动态破坏准则

根据式（2）～（3）计算得到真三轴动态荷载作用下的普通混凝土在八面体应力空间上的剪应力、正应力。为了考虑应变速率对真三轴动态荷载用作下普通混凝土破坏准则的影响，将式（1）改写成：

式中： αε˙、 βε˙、 γε˙为率效应参数；fcd为相应应变速率下的单轴抗压强度。

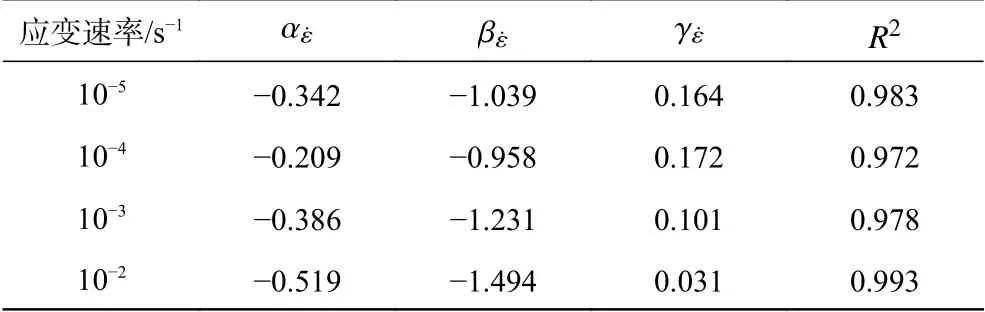
表 2 不同应变速率下破坏准则拟合参数值与相关系数Tab. 2 Fitting parameters and correlation coefficients of failure criterion at different strain rates

利用式（5）对试验数据进行回归分析，得到式（5）中与应变速率相关的参数值见表2。

从表2可以看出，为确定式（5）中率效应参数αε˙、 βε˙、 γε˙与应变速率之间的关系，通过表2中的数据 拟 合 发 现，率 效 应 参 数 αε˙、 βε˙、 γε˙与 应 变 速 率 比ε˙d/ε˙s的对数大致呈二次曲线关系，经过回归分析其

关系式见式（6）～（8），对应的相关系数R2分别为0.80、0.88、0.92。

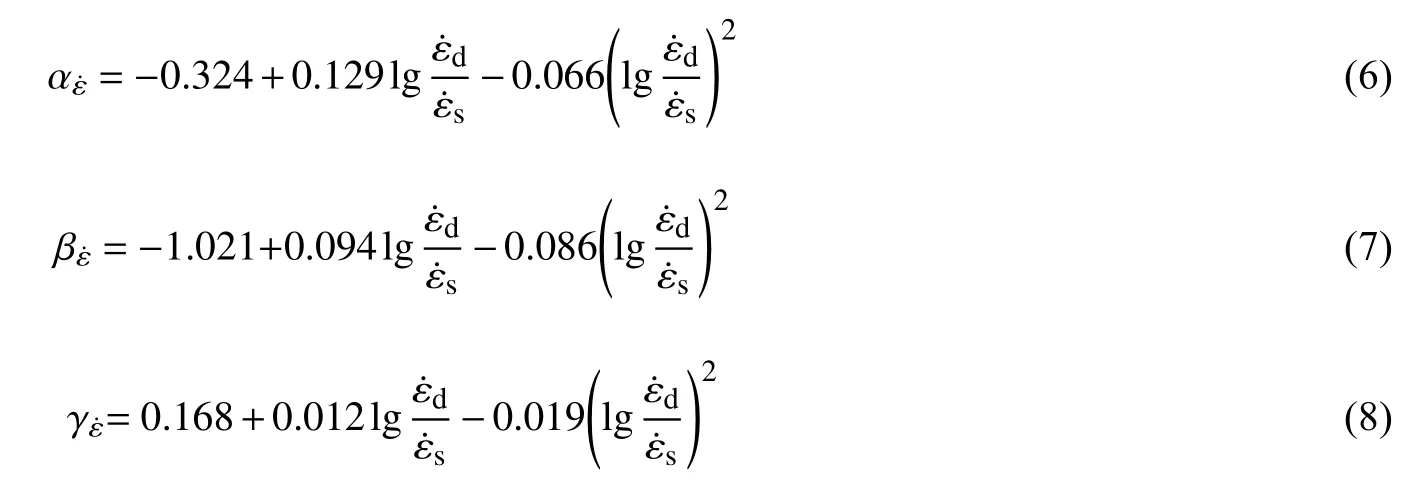
将式（6）～（8）代入式（5）中，得到八面体应力空间下考虑应变速率的普通混凝土真三轴动态破坏准则表达式，见式（9）。

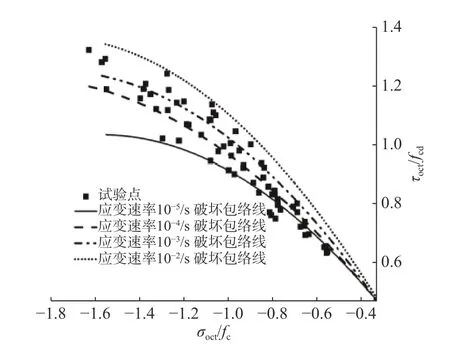
图 5 不同应变速率下混凝土动态破坏准则破坏包络面与试验点Fig. 5 Destruction envelope surface and test points of concrete dynamic failure criterion at different strain rates

5 结 语

本文进行了普通混凝土在不同应力比和不同应变速率下的真三轴静、动态压缩试验，主要结论如下：

（1）与单轴受压相比，处于真三轴受压下混凝土极限抗压强度显著提高。在相同应变速率下，混凝土的极限抗压强度随应力比的增大而增大。当应力比较低时，极限抗压强度随应变速率的增大逐渐增大；当应力比较高时，极限抗压强度随应变速率的增大先减小再增加。

（2）极限抗压强度处对应的轴向峰值应变在侧向所受的应力相等时，随应变速率的增大而整体上呈减小趋势。本文从开展的真三轴动态压缩试验中获得了较为完整的应力-应变曲线，弥补了之前开展的类似试验只有上升段的不足。

（3）随着应变速率的增加，侧向变形曲线的破坏峰值点更突出，轴向抗压强度峰值后曲线下降趋势也更明显。当应力比相同时，侧向的变形情况大致相同；随着应力比的增大，第二主应力方向上的变形越来越小。

（4）建立了受应变速率效应影响的混凝土真三轴动态破坏准则表达式，强度准则曲线光滑外凸且连续，压子午线上八面体剪应力值随八面体正应力值的减小而增大。经验证，所建立的不同应变速率下的破坏包络面表达式与本文试验结果吻合较好。