考虑爆破累积损伤效应的含泥化夹层边坡滑移分析

闫长斌，张彦昌，陈艳国，徐 晓

(1. 郑州大学 土木工程学院，河南 郑州 450001；2. 黄河勘测规划设计研究院有限公司，河南 郑州 450003；3. 中南大学 资源与安全工程学院，湖南 长沙 410083)

泥化夹层是软弱岩石受到构造挤压作用，发生层间剪切错动而使原岩结构遭到破坏形成的一种岩石破碎、结构疏松、黏粒含量高、性状差、强度低、分布广、危害大的软弱结构面，有时也称剪切带[1]。作为一种特殊的软弱结构面，泥化夹层是构成控制边坡岩体稳定性的关键因素[2-3]。许旭堂等[4]研究发现泥化夹层在循环动荷载下疲劳损伤会使其承载力加速降低，进而影响含泥化夹层工程岩体稳定性。孙金山等[5]研究认为，由于受爆破开挖长期影响且受泥化夹层等流变性软弱结构面的控制，含泥化夹层岩质边坡应考虑瞬时损伤累积的影响。泥化夹层诱发边坡失稳机理复杂，在反复爆破等长期动力扰动下，含泥化夹层复杂岩质边坡稳定性评价，更需深入研究。

王思敬[6]率先在国内将滑块分析法应用于边坡动力稳定性分析。此后，该方法在边坡动力稳定性分析中得到广泛应用。唐红梅等[7]根据Newmark滑块位移分析法，对爆破过程中的能量转换过程进行分析，计算了多次爆破振动作用下边坡累积滑移量，并在此基础上根据容许滑移量预测了临界爆破振动次数。然而，需要注意的是，反复爆破振动产生的累积损伤效应会引起边坡岩体，特别是泥化夹层强度参数不断劣化，从而导致边坡整体稳定性降低[8-9]。因此，利用Newmark滑块位移分析法计算边坡累积滑移量时应充分考虑爆破累积损伤效应，引入强度折减系数能使计算结果更加符合实际情况[10]。此外，泥化夹层自身发育特征，如泥化夹层的强度、倾角以及连续率等参数，直接影响边坡的动力稳定性[11-12]。有关泥化夹层自身发育参数对反复爆破振动作用下边坡累积滑移量的影响分析，尚未见诸报道，有待进一步研究。

鉴于此，针对反复爆破振动下含泥化夹层边坡动力稳定分析问题，根据能量守恒定律，基于Newmark滑块位移法，考虑爆破累积损伤效应，引入泥化夹层强度折减系数，建立多次爆破振动下含泥化夹层复杂边坡累积滑移量计算方法和临界爆破失稳作用次数预测方法。结合黄河中游某大型水利枢纽坝址区泥化夹层发育特征和有关室内外试验成果，探讨泥化夹层的剪切模量、倾角及连续率等发育特征参数对多次爆破振动下边坡累积滑移量的影响，对泥化夹层参数敏感性进行分析，为反复爆破振动下含泥化夹层复杂岩质边坡动力稳定性分析与失稳防治提供参考依据。

1 多次爆破振动下含泥化夹层边坡简化模型及其滑移分析

1.1 含泥化夹层边坡爆破振动滑移简化模型

图1为爆破振动作用下含泥化夹层复杂边坡物理模型。假定上覆岩土体为均质刚体，在滑动过程中不考虑体积变化及相应的物理参数变化。

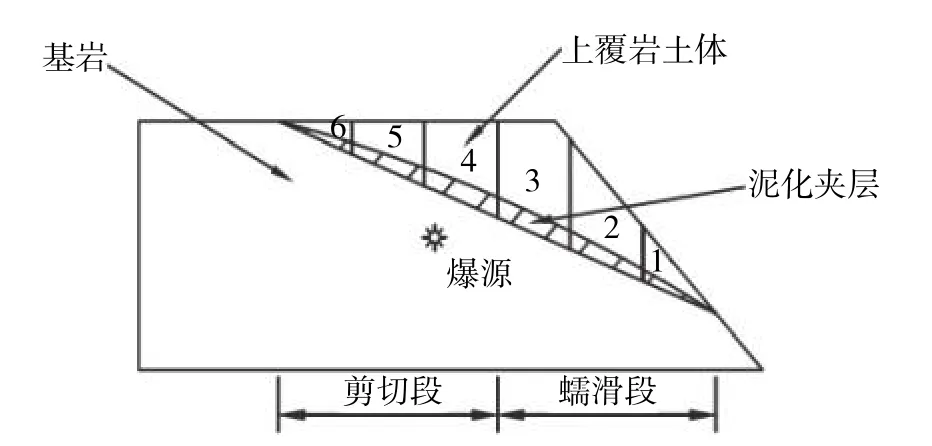
图 1 爆破振动作用下含泥化夹层边坡物理模型Fig. 1 Physical model of complex slope with muddy intercalation under blasting vibration

在振动与降雨等因素作用下，滑体前缘向临空面方向蠕滑变形，同时水的作用使泥化夹层的中部强度降低，形成“牵引式”滑坡失稳模式[13-14]。因此，将泥化夹层及上覆岩土体从右至左划分为6个条块，其中前3个条块为蠕滑段，后3个条块为剪切段。剪切段是泥化夹层中强度和稳定性较高的部分，具有相对较好的抵抗变形的能力；蠕滑段分布在滑体的前缘，由于长期受后缘岩土体的挤压以及水流的侵蚀，其抵抗变形的能力相对较低[7]。爆源处炸药爆炸后，产生的爆破地震波在岩体中传播至泥化夹层处被吸收，转化为泥化夹层的应变能，从而使边坡产生滑移变形。假定泥化夹层为直线型，不考虑泥化夹层的切层转换与起伏差等情况。爆破振动诱发的边坡滑动，实际上是上覆岩土体和泥化夹层一起发生顺层滑动。

1.2 多次爆破振动下含泥化夹层边坡滑移量计算

根据萨道夫斯基公式[15]，爆破振动峰值速度的衰减规律为：

式中：Vm为介质质点振动峰值速度（cm/s）；Q为最大段药量（kg）；R为爆心距（m）；K、α为与爆源至介质质点的地形地质条件有关的系数，一般通过现场试验测定，无试验数据条件时可根据规范[15]选取。

一般而言，爆破振动总能量的衰减系数是爆破振动峰值速度衰减系数的2倍[16]，此时爆破振动衰减至泥化夹层的总能量为：

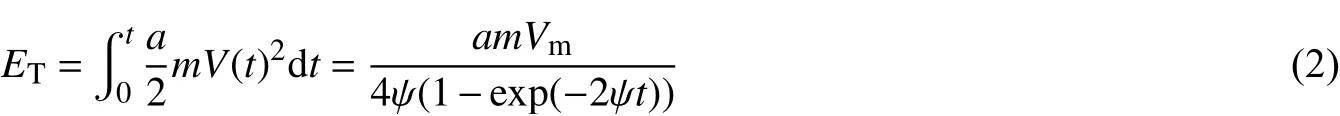
式中：t为爆破地震波作用于边坡的时间（s）；ψ为与爆源至介质质点的地形地质条件有关的衰减系数；m为岩土体质量（kg）；a为初始能量系数，可通过现场测得。

爆破地震波在边坡传播过程中不断衰减，而能量衰减主要集中在泥化夹层处，60 cm厚的泥化夹层就能吸收80%的爆破地震波能量[17]，然后透射到上覆岩土体中。由于上覆岩土体视为刚性体，传播至此处的爆破地震波无法使其发生破坏，在临空面处产生完全反射再次作用于泥化夹层。此时，可假定爆破地震波能量全部在泥化夹层处被吸收，导致泥化夹层产生剪切和蠕变变形[7]。

当爆破振动致使边坡滑动时，泥化夹层中剪切段的应变能[18]可表示为：

式中：u为滑动滑移量（mm）；Ge为泥化夹层的剪切模量（GPa）；l为滑块底面长度（m）。

泥化夹层中蠕滑段的应变能[18]可表示为：

式中：Gs为蠕滑段初始剪切模量（GPa）；u0为蠕滑段剪切模量最大时对应的临界滑移量（mm）。

当边坡发生滑动时，滑块在竖直方向上也会发生相应的位移，这一部分的重力势能将转化为泥化夹层的剪切应变能，作用于泥化夹层的重力势能可表示为：

式中：G为滑块重量（kN）；β为泥化夹层的倾角（°）。

爆破地震波透过泥化夹层后，继续作用于上覆岩土体，而上覆岩土体会阻碍地震波的传播，将一部分爆破地震波吸收，即阻尼效应。阻尼效应的计算式可表示为：

式中：c为上覆岩土体的黏滞阻尼系数；t为爆破地震波的作用时间(s)；V(t)为爆破地震波衰减至上覆岩土体时的速度(m/s)。

为准确表示爆破地震波在任意时刻的速度，可将爆破地震波简化为简谐波，则泥化夹层上覆岩土体的阻尼耗能可表示为[16]：

爆破地震波作用于泥化夹层的过程中，其能量转化为泥化夹层的剪切应变能和上覆岩土体的阻尼耗能。此外，边坡滑动过程中，在竖直方向产生位移导致上覆岩土体重力势能的释放，转化为泥化夹层的剪切应变能。

对于泥化夹层的剪切段，根据能量守恒可得：

联立以上方程式，则剪切段位移计算公式可表示为：

同样，对于泥化夹层的蠕滑段，根据能量守恒可得：

则蠕滑段位移计算公式可表示为：b=Gsinβd=ET−ECh=Gsu20/(2l)

将1次爆破震动作用下各条块的滑移量相累加，即可求出多次爆破震动作用下个条块的总滑移量。

在岩土体滑块阻尼耗能计算过程中，假定爆破地震波能量在泥化夹层及上覆岩土体中被全部吸收。其中，黏滞阻尼系数可根据试验测得，衰减系数及爆破地震波的频率、作用时间均可根据工程现场地质条件进行设定。由于泥化夹层的存在，绝大部分爆破振动能量均被泥化夹层吸收并转化为其应变能，导致上覆岩土体阻尼耗能与爆破地震波产生的能量作用相比数量级相差较大，传播到上覆岩土体的能量总量极少，相对于传播到边坡的总爆破能量几乎可以忽略。基于此，在边坡滑动计算过程中，泥化夹层的存在对边坡滑动起到控制作用，而泥化夹层的发育特征参数，例如剪切模量、倾角和连续率等，直接影响多次爆破振动下边坡累积滑移量。因此，有必要深入研究泥化夹层发育特征参数的影响。

随着爆破振动次数的不断增加，岩体内爆生裂隙不断增加和扩展[19-20]。在此过程中，泥化夹层的强度参数不断劣化，含泥化夹层边坡稳定性不断降低。因此，计算多次爆破振动下边坡的总滑移量时应考虑泥化夹层的强度折减，这样才能反映真实情况，也更为科学合理。影响边坡滑动失稳的泥化夹层强度参数主要是抗剪强度参数，考虑其劣化效应的表达式[10]为：

式中：c和c′分别为考虑折减前、后泥化夹层的黏聚力（kPa）；φ和 φ′分别为考虑折减前、后泥化夹层的内摩擦角（°）；ω为强度折减系数。

为进一步说明在计算多次爆破振动下边坡的总滑移量时考虑爆破累积损伤劣化效应引起的泥化夹层强度参数劣化的合理性，以某隧道工程洞口边坡为例进行分析[18]。该边坡位于陕西省渭河西岸，倾向北东南，稳定性较差，基岩的岩性为弱风化片岩，泥化夹层为角砾土，计算过程中将上覆岩土体视为刚性体，隧道开挖位置位于边坡中部，频繁开挖施工爆破振动严重影响坡体稳定性。

若隧道中心距离滑坡坡脚110 m，距离坡顶70 m[7,21]。据此可建立含泥化夹层边坡模型，确定爆源位置进而确定爆心距，将边坡从左至右划分为6个条块，各条块的爆心距依次为：20.51、19.68、11.36、23.56、35.25和40.41 m。计算建立的边坡模型中各个条块的面积，并向内取为单位长度，求出各个滑块的体积，然后再根据岩土体的重度求出各条块的质量分别为35.525、56.632、77.868、86.525、55.356和30.225 t。

假定岩质边坡的总临界滑移量为670 mm[7]，多次爆破振动下产生的累积滑移量达到总临界滑移量时就会发生滑动失稳。根据文献[16]中的有关研究成果和结论，取泥化夹层的强度折减系数ω为2.8，此时边坡处于极限平衡状态，泥化夹层的有关物理力学参数如表1所示。

表 1 滑体与泥化夹层的有关物理力学参数Tab. 1 Physical and mechanical parameters of sliding mass and muddy intercalation

计算过程中，泥化夹层强度参数按式（12）进行折减后取值。相关的爆破参数如下：装药量Q为44.4 kg，强度折减系数ω为1.8，主频f为20 Hz，时间t为0.5 s，K值为350，衰减系数ψ为10，初始相位θ为0。假定初始能量系数a=10 000，黏滞系数c=0.03。将上述数据代入式（1）～（12），可得到1次爆破振动作用下各条块滑移量（表2）。

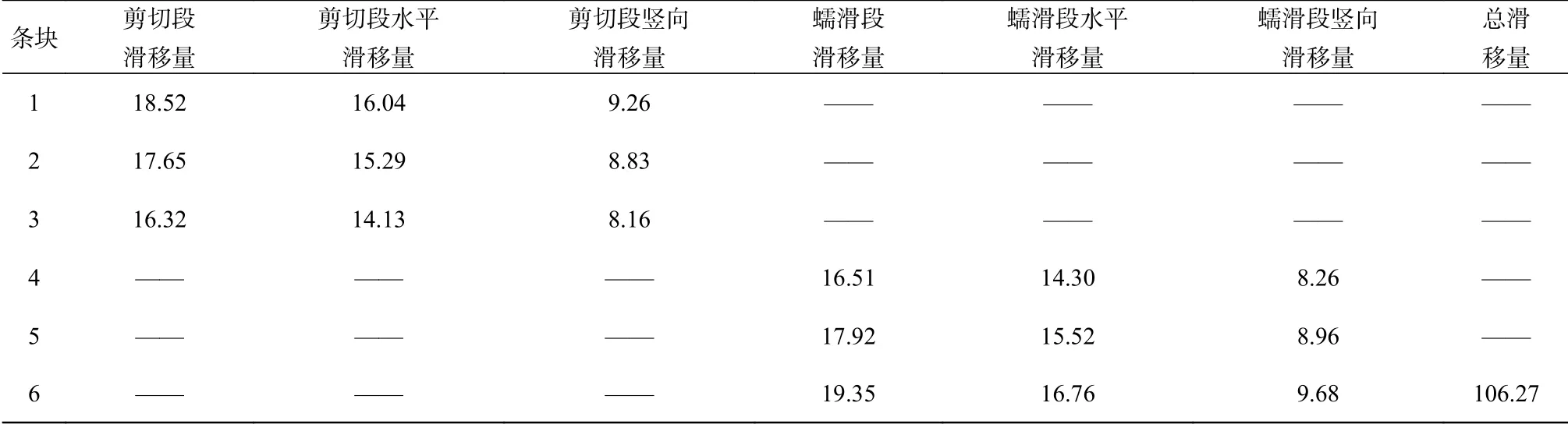
表 2 1次爆破振动下各条块滑移量Tab. 2 Sliding displacement of each block under one blasting 单位：mm

由表2可见，1次爆破振动下边坡的最大滑动滑移量为106.27 mm。假定临界滑移量为670 mm，则经过6.31次爆破振动作用，边坡便会发生失稳破坏。如果不考虑泥化夹层随爆破次数增加产生的强度折减，则需要经过7.98次爆破振动才会发生失稳破坏，而实际工程中经过6次爆破边坡即发生破坏[7]。可见，在计算多次爆破振动下边坡累积滑动滑移量时，考虑爆破累积损伤效应引起的泥化夹层强度参数劣化，更符合工程实际情况。以此为基础，估算临界爆破振动作用次数，相对更安全。

3 泥化夹层参数对多次爆破振动下边坡累积滑移量的影响

3.1 泥化夹层发育特征与参数取值

黄河中游某大型水利枢纽工程坝址区为近水平状单斜地层，总体上走向10°～30°，倾向NW，倾角0°～3°。地质构造简单，未发现断层、褶皱等构造，发育有陡倾角节理裂隙和泥化夹层等[4,22]，主要岩性有长石砂岩、泥质粉砂岩、钙质粉砂岩、细砂岩以及泥岩等。泥化夹层一般为顺层发育，母岩多为紫红色泥岩或泥质粉砂岩，发育厚度不等，多为3～15 mm。大多数泥化夹层延伸和连续性均较好，且厚度越大越连续；发育类型主要有岩块岩屑型、岩屑夹泥型、泥夹岩屑型和泥型等4种，其中泥夹碎屑型和泥型的黏粒含量较高，强度较低。钻孔揭露的泥化夹层发育情况如图2所示，图中泥化夹层的厚度约15 mm。

图 2 钻孔揭露的泥化夹层发育情况Fig. 2 Muddy intercalations investigated by drillings

为确定泥化夹层的发育特征和相关参数，在现场勘察平硐中选取代表性泥化夹层进行取样，并开展了相应的室内土工试验和动三轴试验，得到了泥化夹层的发育类型、倾角大小、连续性以及动静条件下的物理力学参数（包括含水率、密度、弹性模量、泊松比、内摩擦角、黏聚力等）。选取的泥化夹层平硐发育情况及泥化夹层样品现场采取，见图3所示。

其中，平硐PD207揭露的泥化夹层，发育于青灰色长石砂岩与紫红色钙质粉砂岩层间，泥化发育程度较高，连续性好，厚度约5～30 mm。平硐PD215揭露的泥化夹层上下岩体均为砂岩，类型较复杂，以岩屑夹泥型为主，连续性较差，厚度相对较薄，约为3～20 mm。平硐PD302揭露的泥化夹层发育于粉砂岩与砂岩之间，泥化程度高，连续性好，厚度约为3～80 mm。

泥化夹层发育特征对多次爆破振动下含泥化夹层边坡累积滑移量的影响十分复杂，既包括泥化夹层的物质成分组成、几何形态特征，也包括含水状态、厚度特征等。根据工程实践，这里主要考虑3个方面，即强度参数（考虑了含水状态和物质组成的影响）、几何状态和连续性，并确定剪切模量、倾角和连续率等3个主要参数。由于坝址区泥化夹层厚度变化不大，这里暂不考虑厚度影响。根据现场勘察和室内外试验成果，对选取的泥化夹层剪切模量、倾角和连续率，分别取3个不同数值，按三因素三水平进行正交试验设计，得到分析计算工况，见表3。根据表3中列出的计算工况，可分别分析泥化夹层的剪切模量、倾角和连续率等参数变化对多次爆破振动下含泥化夹层边坡累积滑移量的影响。

图 3 平硐揭露的泥化夹层及现场取样Fig. 3 Muddy intercalations investigated by adits and their in-situ sampling

表 3 泥化夹层参数分析计算工况Tab. 3 Parameter analysis and calculation of muddy intercalations

3.2 泥化夹层参数对边坡爆破累积滑移量的影响

坝址区边坡为缓倾角顺层状含泥化夹层复杂岩质边坡，泥化夹层发育在边坡的中上部，泥化夹层的下部基岩为砂岩，上覆岩土体为粉砂岩，泥化夹层构成影响边坡整体稳定的控制性软弱结构面。参考图1中给出的边坡物理模型，可将泥化夹层及其上覆岩土体划分为6个条块。假定爆源距离坡顶和坡脚分别为50和60 m，相关爆破参数取值同前。根据现场勘察和室内外试验成果，边坡岩土体和泥化夹层的有关参数取值见表4。考虑爆破累积损伤效应引起的泥化夹层强度参数折减，折减系数根据前述分析，取2.80[10]。若临界滑移量为670 mm[7]，考虑最不利情况，即泥化夹层剪切模量为43 MPa，倾角为20°，连续率为100%，经计算可知，经过9.52次爆破振动，边坡即发生滑动失稳。因此，以9次爆破振动下边坡累积滑移量为例，分别分析泥化夹层参数对边坡累积滑移量的影响。

表 4 坝址区滑体与泥化夹层的有关物理力学参数Tab. 4 Physical and mechanical parameters of sliding mass and muddy intercalation at the dam site

3.2.1 泥化夹层的剪切模量 假定泥化夹层倾角为20°，连续率100%，可分析泥化夹层剪切模量对边坡累积滑移量的影响。根据表3列出的计算工况，考虑爆破累积损伤效应引起的泥化夹层强度参数折减，可分别计算剪切模量为43、51和56 MPa时，经过9次爆破振动后，含泥化夹层边坡的总累积滑移量分别为633.07、564.85和516.25 mm。可见，当其他条件不变时，随泥化夹层剪切模量的增大，边坡累积滑移量逐渐减小。

3.2.2 泥化夹层的倾角 假定泥化夹层剪切模量为43 MPa、连续率为100%，可分析泥化夹层倾角对边坡累积滑移量的影响。根据表3列出的计算工况，考虑爆破累积损伤效应引起的泥化夹层强度参数折减，可分别计算泥化夹层倾角为10°、15°、20°时，经过9次爆破振动后，含泥化夹层边坡的总累积滑移量分别为557.83、586.45和633.07 mm。可见，当其他条件不变时，随着泥化夹层倾角的增大，边坡累积滑移量逐渐增大。在计算过程中还发现，剪切段累积滑移量变化不大，但蠕滑段累积滑移量显著增加，总体上边坡累积滑移量表现为逐渐增大。

3.2.3 泥化夹层的连续率 假定泥化夹层剪切模量为43 MPa，倾角为20°，可分析泥化夹层连续率对边坡累积滑移量的影响。根据表3列出的计算工况，考虑爆破累积损伤效应引起的泥化夹层强度折减，可分别计算泥化夹层连续率为33%、67%、100%时，经过9次爆破振动后含泥化夹层边坡的总累积滑移量分别为559.72、588.88和633.07 mm。可见，随泥化夹层连续率的增大，边坡累积滑移量逐渐增大，泥化夹层连续性直接影响边坡稳定性。

4 泥化夹层参数敏感性分析

为进一步探究泥化夹层参数对多次爆破振动下边坡累积滑移量的影响程度，可进行参数敏感性分析。泥化夹层参数与边坡累积滑移量之间的相互关系，可通过边坡累积滑移量的相对变化率与各个泥化夹层参数的相对变化率之间的比值来体现，第i个参数的敏感度Si表达式如下：

式中：Fi为边坡累积滑移量的初始值；ΔFi为边坡累积滑移量的变化量；Xi为指定分析参数的初始量；ΔXi为指定分析参数的变化量。

由式（13）可知，敏感度Si是参数变化量ΔXi的函数，通过计算不同泥化夹层参数条件下边坡累积滑移量的变化，即可得到各参数的敏感度Si，最终确定各参数对边坡累积滑移量的影响程度。据前所述，按照最不利条件考虑，在对各参数进行敏感性分析过程中，计算多次爆破振动下边坡累积滑移量时，仍考虑9次爆破振动作用。

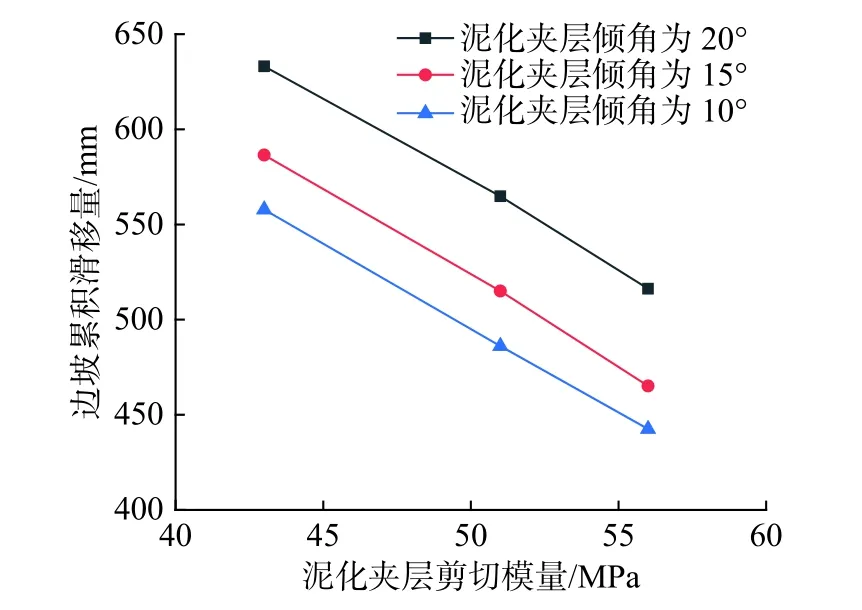
图 4 边坡累积滑移量随泥化夹层剪切模量的变化Fig. 4 Variation of slope cumulative sliding displacement with shear modulus of muddy intercalation

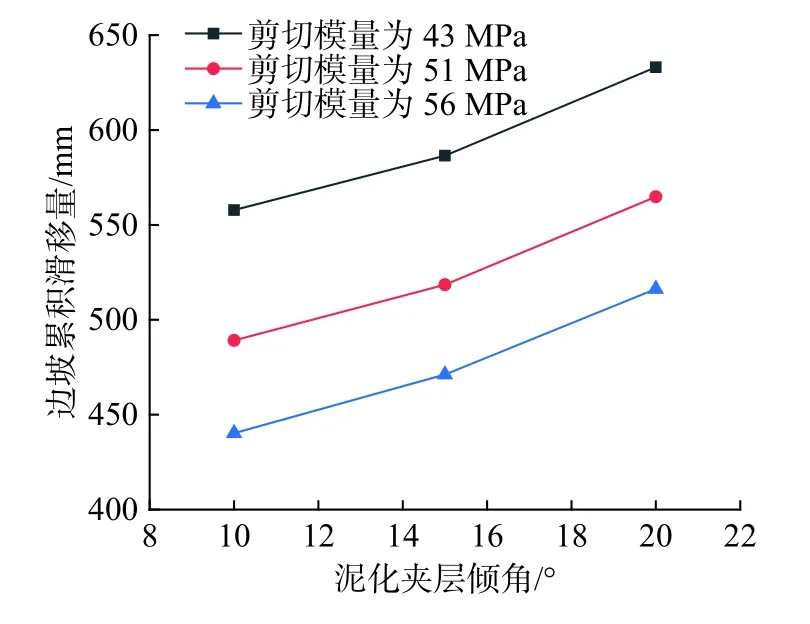
图 5 边坡累积滑移量随泥化夹层倾角的变化Fig. 5 Variation of slope cumulative sliding displacement with dip angles of muddy intercalation

4.1 剪切模量

假定泥化夹层的连续率为100%，分别计算不同的泥化夹层倾角下，边坡累积滑移量随着剪切模量的变化情况，计算结果如图4所示。由图4可见，在不同的泥化夹层倾角下，边坡累积滑移量与剪切模量之间均呈较明显的线性递减关系，即边坡累积滑移量随泥化夹层剪切模量增大逐渐减小。根据相对变化率大小，可计算得到泥化夹层剪切模量的敏感度S1=0.610。

4.2 倾 角

假定泥化夹层的连续率为100%，可分别计算在不同的剪切模量下，边坡累积滑移量随泥化夹层倾角的变化情况，计算结果如图5所示。由图5可见，在不同的泥化夹层剪切模量下，边坡累积滑移量与泥化夹层倾角之间呈较明显的近似线性递增关系，边坡累积滑移量随泥化夹层倾角的增大而增大。根据相对变化率，可计算得到泥化夹层倾角的敏感度S2=0.135。

4.3 连 续 率

假定泥化夹层的倾角为20°，分别计算在不同的剪切模量下，边坡累积滑移量随泥化夹层连续率的变化情况，计算结果如图6所示。由图6可以得出，在不同的泥化夹层剪切模量下，边坡累积滑移量与泥化夹层连续率之间均呈较明显的近似线性递增关系，随泥化夹层连续率的增大而增大。根据相对变化率，可计算得到泥化夹层连续率的敏感度S3=0.065。

根据参数敏感性分析，可得S1> S2> S3，即选取的3个泥化夹层参数中，对边坡爆破累积滑移量的影响程度依次为剪切模量、倾角和连续率。由此可见，泥化夹层的强度指标（剪切模量）对含泥化夹层边坡爆破累积滑移量起控制作用。

图 6 边坡累积滑移量随泥化夹层连续率的变化Fig. 6 Variation of slope cumulative sliding displacement with continuities of muddy intercalation

5 结 语

（1）可利用Newmark滑块位移法计算多次爆破振动下含泥化夹层复杂岩质边坡累积滑移量，以此作为评价边坡动力稳定性的依据，并预测边坡临界失稳爆破作用次数。

（2）多次爆破振动下考虑累积损伤效应引起的泥化夹层强度参数劣化，引入强度折减系数，边坡累积滑移量计算结果和临界失稳爆破作用次数预测结果更接近实际情况。

（3）泥化夹层发育特征及其参数对多次爆破振动下边坡累积滑移量具有显著影响。随泥化夹层剪切模量增大，边坡累积滑移量减小；随泥化夹层倾角增大，边坡剪切段滑移量无明显变化，但蠕滑段滑移量明显增大，总的累积滑移量随之增大；泥化夹层连续率越高，边坡累积滑移量越大。

（4）参数敏感性分析结果揭示，泥化夹层的剪切模量对多次爆破振动下边坡累积滑移量影响最为显著，其次是泥化夹层的倾角，再次是泥化夹层的连续率。