BDS-2/3与GPS 短基线相对定位精度评定与分析
付 贵,杨 萍,高 翔
(1.贵州建设职业技术学院,贵州 贵阳 551400;2.贵州省测绘产品质量监督检验站,贵州 贵阳 550004;3.安徽理工大学测绘学院,安徽 合肥 232001)
2020 年 7 月 29 日,北斗卫星导航系统(BeiDou satellite navigation System,BDS)的最后一颗卫星顺利完成入网工作,标志着 “三步走”发展战略圆满完成,BDS 迈进全球服务新时代。随着BDS 最终组网完成,BDS 应用将迅速发展。定位、导航与授时 (Position,Navigation,and Timing,PNT)[1]作为全球卫星导航系统 (Global Navigation Satellite System,GNSS)的基本功能,BDS 星座异构[2]、精密单点定位 (Precise Point Positioning,PPP)载荷和星间链路[3]等特色,让BDS 在PNT 应用端具备更大的潜力。其中,短基线相对定位方式的高精度优势,使其在区域连续运行 (卫星定位服务)参考 站 (Continuously Operating Reference Stations,CORS)服务[4]和变形监测[5]等方面表现突出。目前,短基线相对定位能够提供毫米级甚至亚毫米级的定位服务[6]。
动态定位方式和静态定位方式为不同应用提供高精度服务。动态定位即单历元解算,在变形监测等方面起到重要作用[7-8]。陈永奇等[7]讨论了单历元解算在变形监测中的应用,并分析了该方法的数据处理精度;余学祥等[8]提出基于监测网和卫星的空间关系,利用载波相位观测值直接建立单历元解算变形的数学模型,获得了毫米级的定位精度;刘炎炎等[9]基于BDS 三频的短基线单历元解算,模糊度固定成功率达到100%。静态定位通常为获取测站精确的点位信息,在没有高等级控制点的情况下,替代高等级控制点。姚连壁等[10]分析了全球定位系统 (Global Positioning System,GPS)短基线静态相对定位在道路和交通工程等领域应用的可行性;赵庆志等[11]基于GPS 静态相对定位技术,在剔除粗差的前提下,满足了城市建设和城市规划的要求。
鉴于BDS 的星座异构特点和对BDS 相对定位精度的探究较为贫乏,本文基于动态短基线相对定位方式,分析BDS-2/3 定位较GPS 定位的优缺点。
1 BDS 卫星轨迹分析
本文数据采集于某高校 (纬度约为32°N)的两台CORS,两台CORS 之间的距离约为13 m,采样频率为1 Hz,卫星截止高度角为15°。这两台CORS 于 2019 年 10 月 12 日接收 BDS 和 GPS 的卫星观测数据。
BDS共接收到25 颗卫星的观测数据,其中,C01/C02/C03/C04 这 4 颗卫星为地球同步轨道(Geosynchronous Earth Orbit,GEO) 卫星,C06/C07/C08/C09/C10/C13/C16 这7 颗卫星为倾斜同步轨 道 (Inclined Geosynchronous Satellite Orbit,IGSO) 卫星,其余 14 颗卫星为中地球轨道(Medium Earth Orbit,MEO)卫星。GEO 相对于地球处于静止状态,天空图中为点状;IGSO 的卫星轨迹为 “8”,轨道运行周期约为23 h 55 min 30 s;BDS 的MEO 的轨道高度低于前两者,这使得MEO在定位时起到主导作用,其轨道运行周期约为7 d。值得一提的是,其中有13 颗卫星为BDS-2 卫星,12 颗为 BDS-3 卫星。
GPS 共接收到30 颗卫星 (G04/G14 处于异常状态)的观测数据,其卫星均为MEO,具有3 种卫星类型,分别为Block IIR,Block IIR-M 和Block IIF。
2 BDS 与GPS 的定位精度分析
本文基于RTKLIB 标准与精密定位开源程序包进行双频 (B1/B3)单历元解算,其中模糊度固定模式采用固定并保持 (fix-and-hold)模式。由于两台CORS 之间的距离较近,高程上无明显差异,且接收机类型一致,因此可认为该基线仅受到多路径误差和噪声影响。
根据BDS 和GPS 的E,N,U 方向三维坐标序列可知,针对E 方向和N 方向,BDS 坐标序列的幅值波动较小,GPS 波动较大,该现象表明BDS 抗多路径误差能力优于GPS,而U 方向无明显区别,说明U 方向定位精度在较大程度上受限于定位的数学模型。
虽然在幅值波动上GPS 大于BDS,但明显可观测到二者的噪声水平并不相同。本文基于经验模态分解 (Empirical Mode Decomposition,EMD)方法提取噪声,计算其信噪比(Signal-to-Noise Ratio,SNR)RSN,计算公式为
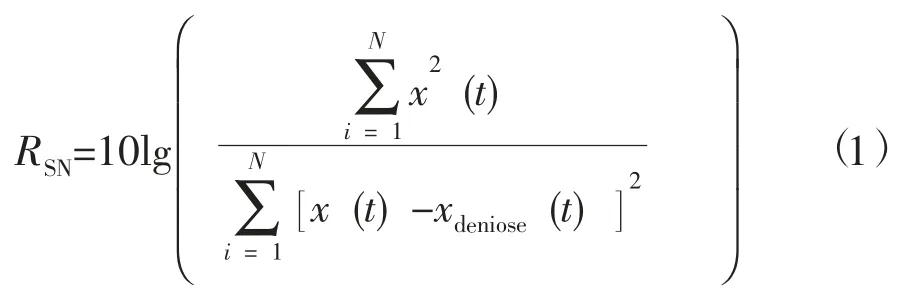
式中:N 为历元数;x (t) 为原始序列;xdenoise(t) 为降噪后序列。
此外,为评价BDS 和GPS 的定位精度,使用BDS/GPS 组合定位下的静态解算数据 (11.405 4,6.007 9,0.019 9)作为真值,评价均方根误差(Root Mean Square Error,RMSE) εrms和偏差指标Ibias,计算公式分别为
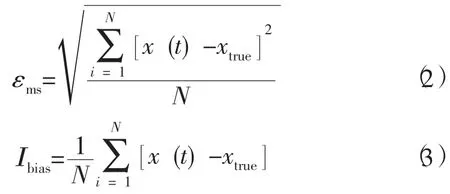
式中:xtrue为真值。
表1 给出了BDS 和GPS 的各评价指标。由表1可知,BDS 的E 方向和N 方向的 εrms均明显优于GPS的定位精度,充分说明星座异构的BDS 在平面方向上的定位精度优于GPS 的定位精度,此外,U方向BDS 与GPS 的定位精度相当,甚至优于GPS。从Ibias可以看出,E 方向和U 方向BDS 和GPS 基本保持一致,N 方向较GPS 相差较大,说明在N 方向的BDS 内符合定位精度略差于GPS。RSN是评价观测数据的噪声功率占比,RSN越大,表明噪声越少。由表1 可知,BDS 在3 个方向的RSN对应均差于GPS,这主要是由于BDS 存在较多的浮点解,模糊度固定成功率较低。

表1 BDS 和GPS 的各评价指标
3 可视卫星数和模糊度固定率分析
两台CORS 之间的距离较近,共视卫星数相等。其可视卫星数在一定程度上决定了定位精度,以下研究BDS 和GPS 的可视卫星数。
BDS 的可视卫星数平均为12.3 颗,平均每个历元能观测到12 颗卫星;GPS 的可视卫星数平均为7.6 颗。由于BDS 有4 颗卫星为GEO 卫星,因此保证了每个历元均能够观测到卫星;并且由于BDS 有7颗卫星为IGSO 卫星,因此增强了亚太地区的观测质量,这是保证BDS 的可视卫星数的重要因素。BDS 可视卫星数经常性出现波动,主要因为其中的C02 号卫星会出现卫星信号失锁现象。卫星的出现或消失均会使双差观测方程数和卫星组合方式改变,使得其需要重新计算模糊度。一般以比率(ratio)值Iratio为评价模糊度固定成功与否的指标[12],当Iratio<3 时,认为是浮点解;Iratio≥3 时,认为是固定解。为方便观测指标,本文以1/Iratio来评价,即1/3 为分界。
根据实测数据可知,GPS 的模糊度固定成功率要显著优于BDS,其主要原因在于GPS 卫星均为MEO 卫星,卫星信号强度足够;而BDS 的GEO 卫星处于36 000 km 高空,电磁波信号衰减问题严重。并且,BDS 卫星消失或出现,会经常引起模糊度的重新搜索。其中,GPS 的模糊度固定成功率为99.85%,而BDS 的模糊度固定成功率为96.72%。
4 结论
本文对比分析了BDS 和GPS 的短基线相对定位,获得以下结论。
1)在BDS 的短基线相对定位中,抗多路径误差能力强,坐标序列幅值波动小于GPS 坐标序列。其中,BDS 双频定位的E,N,U 方向精度分别为1.791 mm,2.354 mm 和7.491 mm,与此同时GPS双频定位的E,N,U 方向精度分别为2.477 mm,2.918 mm 和7.686 mm。在平面方向上BDS 的定位精度要明显优于GPS,在垂直方向上二者的定位精度相当。
2)BDS 的可视卫星数量平均每历元可观测到12 颗卫星以上,GPS 为7 颗卫星以上。其中,GPS的模糊度固定成功率要显著优于BDS,其主要原因在于卫星出现或消失导致模糊度重新搜索。未来的主要工作需围绕随机模型策略和选星等方面展开,以提高BDS 相对定位的模糊度固定率等性能。

