基于等效介质理论的孔隙纵横比分布反演

欧阳芳， 赵建国， 李智， 肖增佳， 贺艳晓， 赵皓， 任静

中国石油大学(北京)油气资源与探测国家重点实验室， 北京 102249

0 引言

岩石的弹性性质受孔隙度、孔隙结构、矿物成分、及流体性质等多种因素的综合影响，其中孔隙结构是影响岩石特性的重要因素.由于岩石孔隙空间分布十分复杂，孔隙结构难以定量表征，因此需要借助理想的几何形状对复杂的孔隙结构进行近似处理.目前，最常用的孔隙结构表征方法是将岩石中的孔隙包含物近似为椭球体，并采用椭球体的短长轴之比(即孔隙纵横比)作为描述孔隙结构特征的主要参数.为了研究椭球状孔隙包含物的弹性性质，Eshelby(1957)基于弹性理论和假想实验建立了椭球包含物弹性质及其几何形状与岩石基质弹性模量之间的内在联系，并给出了椭球包含物的弹性场表达式.在Eshelby理论的基础上，Wu(1966)与Dunn和Ledbetter(1995)进一步推导了椭球孔隙压缩系数P和剪切柔度Q的解析表达式，其中P和Q又称为孔隙几何因数(Mavko et al., 2009)，它们均为孔隙包含物弹性模量、孔隙纵横比、以及其所在背景基质弹性模量的函数，是描述椭球孔隙结构特征的重要参数.这一系列工作为基于椭球孔隙包含物假设的各种岩石物理模型的建立和发展奠定了重要理论基础.

等效介质理论是联系岩石微观孔隙结构与岩石等效弹性性质的重要桥梁.目前，运用较为广泛的等效介质理论包括：Kuster-Toksöz(KT)模型(Kuster and Toksöz，1974)、Mori-Tanaka(MT)模型(Mori and Tanaka，1973；Benveniste，1987； Ferrari，1994)、自相容近似(Self-Consistent Approximation, SCA)模型(Budiansky，1965；Berryman，1980;Berryman and Wang, 1995；Wu，1966)和微分等效介质(Differential effective medium, DEM)模型(Zimmerman，1984；Norris，1985；Berryman et al.，2002；李宏兵和张佳佳，2014).KT模型由Kuster和Toksöz(1974)在长波长假设条件下基于散射理论推导得到，具有计算岩石等效弹性性质的显式表达式.与KT模型类似，MT模型也具有显式的解析理论公式，因此KT模型和MT模型的数值实现十分简单，且更便于实际应用.但已有研究表明，KT模型和MT模型仅适用于包含物稀疏分布的情形(Kuster and Toksöz，1974；Berryman and Bergr，1996；Mavko et al., 2009)，并且在某些条件下，KT模型和MT模型的等效弹性模量可能会超出Hashin-Shtrikman界限(Berryman，1980；Norris，1989；Ferrari，1991).Berryman和Bergr(1996)指出，只有当岩石基质占岩石总体积的比例高于70～80%时，KT模型和MT模型才能得到比较合理的结果.因此，在运用KT和MT模型时需十分谨慎.与显式的KT 模型和MT模型不同，SCA模型和DEM模型属于隐式耦合模型，这些模型均涉及一系列迭代或微分运算.尽管SCA模型和DEM模型的计算相对复杂，但它们考虑了包含物之间的弹性相互作用，从而可以将孔隙包含物推广到含量稍高的情况(Mavko et al., 2009).在上述等效介质模型中，岩石等效弹性模量均为孔隙纵横比和孔隙度的非线性复杂函数.由此可见，孔隙结构参数的获取对等效介质理论的有效运用十分重要.

一直以来，许多学者尝试采用各种方式从实际数据中提取孔隙纵横比，根据这些方法的反演结果，大致可以分为两类：等效纵横比反演法和纵横比分布反演法.等效纵横比反演法通常假设岩石仅含一组或两组孔隙，并利用实际数据(如岩芯数据、测井数据等)反演计算各组孔隙的等效纵横比，比如：Kumar和Han (2005) 假设岩石孔隙空间仅由两种孔隙构成，即背景孔和球形孔或背景孔和微裂隙，利用Wyllie时间平均方程和DEM模型，由含水饱和碳酸盐岩的实测速度反演计算两种孔隙的等效孔隙纵横比及体积含量；之后， Xu和Payne(2009)在此基础上提出了适用于碳酸盐岩的Xu-Payne模型；Zhao等(2013)进一步将该建模思路应用于测井和地震数据的孔隙纵横比反演；Fortin等(2007)与Adelinet等(2011)假设岩石由球形硬孔和单一纵横比的微裂隙构成，在各个压力下分别对砂岩和玄武岩进行了孔隙纵横比反演；De Paula等(2012)提出了一种由干燥岩石纵横波速度-压力数据获取中孔(即纵横比介于0.01和0.2之间的孔隙)和软孔(即纵横比小于0.01的孔隙)等效孔隙纵横比的反演方法；郭继亮等(2017)采用单重孔隙岩石物理模型对碳酸盐岩孔隙形态参数(或孔隙纵横比)和孔隙度进行了反演；李宏兵等(2019)基于单一孔隙纵横比的DEM模型建立了复杂孔隙储层的三维岩石物理量版.

尽管等效纵横比法实现简单且容易应用，但球状硬孔隙的假设通常难以满足实际情形；此外，微裂隙对压力的变化十分敏感，假设所有微裂隙仅具有一个“等效纵横比”而不考虑压力对孔隙形态的影响往往是不够的.与等效纵横比反演不同，纵横比分布反演法认为岩石的孔隙空间是由一系列纵横比不同的孔隙构成的，因而更符合实际条件.早在20世纪60年代，Walsh(1965)便指出，岩石纵横波速度的压力依赖性是由岩石中孔隙的闭合引起的；不久，Morlier(1971)和Toksöz等(1976)根据速度与压力之间的变化关系，提出了孔隙纵横比分布的反演思路；之后，Cheng和Toksöz(1979)、Zimmerman(1991)与David和Zimmerman(2012)进一步将孔隙纵横比分布反演法与等效介质理论结合起来.在这些孔隙纵横比反演方法中，David和Zimmerman(2012)的孔隙结构模型(简称D-Z模型)最为经典，该模型假设岩石由固体矿物基质、一组纵横比相等的硬孔隙以及多组纵横比不等的微裂隙构成，并认为固体矿物基质和硬孔隙均不受压力影响，然后以累积裂隙密度为桥梁，借助等效介质理论将岩石弹性模量和孔隙纵横比联系起来；并在此基础上，利用超声纵横波速度的压力依赖性反演岩石硬孔隙和各组微裂隙的孔隙纵横比及孔隙度.尽管D-Z模型能够获得岩石的完整孔隙纵横比分布，但在该模型中，多重孔隙岩石的累积裂隙密度是由单重孔隙条件下的裂隙密度公式近似计算得到的，而这种近似处理导致D-Z模型在许多情况下无法获得良好的反演精度.此外，D-Z模型仅考虑了DEM和MT理论，而在许多情况下，KT和SCA等其他等效介质理论的应用也十分广泛.

为此，本文提出一种基于虚拟降压的孔隙纵横比分布反演方法，将基于DEM和MT的经典D-Z模型推广到KT和SCA中，结合四种等效介质理论建立了一套完整的反演流程，该流程通过模拟假想降压过程实现累积裂隙密度的准确反演，从而有效克服经典D-Z模型的精度不足.本文首先简要回顾了四种等效介质模型的基本理论；然后，根据压力对孔隙形态的影响规律，推导了微裂隙孔隙纵横比和裂隙密度的计算公式；在此基础上，给出了基于虚拟降压的孔隙纵横比分布反演流程；最后，应用实际岩芯数据对该反演方法进行了测试和分析.

1 等效介质理论的基本公式

等效介质理论是联系微观孔隙结构与岩石弹性性质的重要工具.本文假设岩石孔隙形状均为扁圆椭球体状(见图1，图中α表示孔隙纵横比，a和c分别为椭球孔的长轴和短轴)，并利用KT模型、MT模型、DEM模型和SCA模型四种不同的等效介质理论实现硬孔隙和微裂隙孔隙纵横比的反演计算.这里我们首先回顾四种等效介质理论的基本公式.

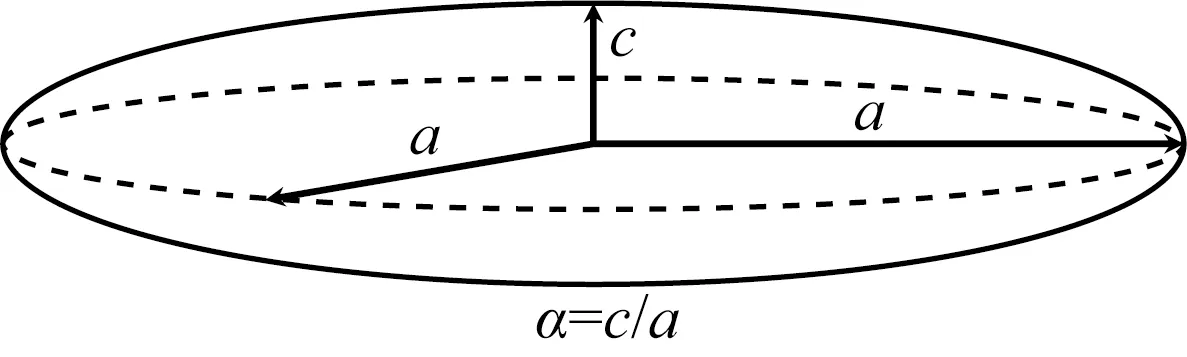
图1 扁圆椭球状孔隙Fig.1 The oblate-ellipsoid pore

1.1 KT模型

基于散射理论，Kuster和Toksöz(1974)推导了多重孔隙岩石的Kuster-Toksoz表达式，其一种推广形式可以表示为

(1)

以及

(2)

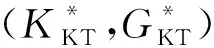
对于单重孔隙的干燥岩石，即N=1且Ki=Gi=0，式(1)可以简化为

(3)

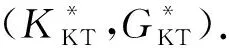
1.2 MT模型

根据Mori-Tanaka理论(Mori and Tanaka, 1973)，多重孔隙岩石的等效弹性模量满足如下方程(Berryman and Berge, 1996)：

(4)

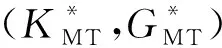
如果岩石仅由体积百分比分别为1-φ和φ的矿物基质和单重孔隙构成，则式(4)可以退化为

(5)

式中，(Km,Gm)为岩石矿物基质的体积模量和剪切模量；(Ki,Gi)为孔隙包含物的体积模量和剪切模量.上述过程运用了关系Pmm=Qmm=1，此式表明当孔隙包含物材料与主相材料相同时，几何因数为1.在干燥条件下，式(5)还可以进一步简化为

(6)

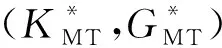
1.3 DEM模型

在多重孔隙情形下，Norris形式的DEM公式可以写成(Norris, 1985; 李宏兵和张佳佳, 2014)

(7)

上述微分方程满足初始条件：

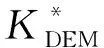
(8)

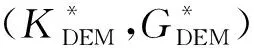
在干燥条件下，上述耦合微分方程具有解析近似式，即(李宏兵和张佳佳, 2014)

(9)

式中，a,b,S0i,S1i,S2i和S3i的具体表达式详见附录B.

1.4 SCA模型

Berryman(1980; Berryman and Wang,1995)给出了N相混合物的自相容近似(SCA或CPA)的一般形式：

(10)

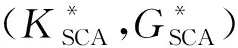
对于由矿物基质和单重孔隙构成的两相混合物，Wu(1966)给出了如下自相容模量的计算公式：

(11)

在干燥条件下，上式变为

(12)

这里需要注意的是，尽管式(10)和式(11)均为SCA模型公式，但两者来源却完全不同.通常，如果一个模型既能由准静态分析得到，也能通过散射近似获得，则称该模型为“物理可实现”，否则称“物理不可实现”.在上述公式中，Berryman提出的SCA模型为“物理可实现”模型，而Wu提出的SCA模型为“物理不可实现”模型.事实上，KT模型和MT模型均为“物理不可实现”模型，而DEM模型为“物理可实现”模型(Berryman and Bergr, 1996).虽然“物理不可实现”模型无法适用于所有类型的孔隙形状，但对于许多形状(如球形)，它们仍能给出十分准确的估计结果.

2 微裂隙孔隙纵横比及裂隙密度

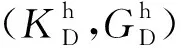
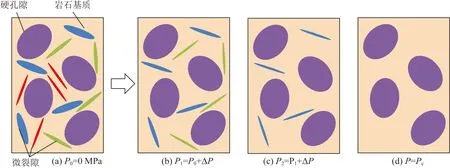
图2 受压后岩石内部硬孔隙和微裂隙的形态变化示意图Fig.2 Schematic diagram of stiff pores and micro-cracks in rock at different hydrostatic pressures

(13)

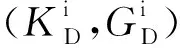
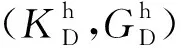
2.1 孔隙纵横比的理论公式

下面我们从微裂隙随有效压力的变化规律出发，推导微裂隙孔隙纵横比的计算公式.考虑压力P下某一个纵横比为α的干燥硬币形微裂隙(即近似于孔隙纵横比很小的扁椭球孔隙)，由压缩定律可知，其相对体积变化为

dVc(P)/Vc(P)=-Cc(P,α)dP,

(14)

式中，Cc(P,α)表示压力P下纵横比为α的微裂隙的压缩系数；Vc(P)表示压力P下微裂隙的体积，dVc(P)为相应的体积变化量.在微裂隙的闭合过程中，通常假设其长轴a保持不变，即dVc/Vc=dα/α.因此，式(14)变为

dα=-[αCc(P,α)]dP,

(15)

当α很小(即α→0)时，有(Zimmerman, 1991)

(16)

即αCc(P,α)与α无关.式中，K和ν分别为体积模量和泊松比.

将式(15)从0到P进行积分，得到

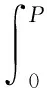
(17)

式中，α0表示零压力下的微裂隙初始纵横比；第二项表示压力由0变化至P的过程中微裂隙纵横比的变化量.此外，硬币形微裂隙的纵横比通常较小(<0.01)，因此第二项几乎是与α无关的(参见式(16))，这便意味着，在相同的压力变化区间内，所有微裂隙的纵横比变化量是相同的.

假设该微裂隙的闭合压力p等于P，即α(P)=0，则式(17)变为

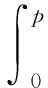
(18)

式中，α0(p)表示闭合压力为p的微裂隙的初始孔隙纵横比，在后文中，闭合压力均用p表示，以与P相区分.上式表明，当压力由0增至该微裂隙的闭合压力p时，其纵横比变化量刚好等于其初始纵横比大小，即当施加的有效压力P等于微裂隙的闭合压力p时，微裂隙刚好完全闭合.注意，利用式(18)为计算单一微裂隙的孔隙纵横比公式，需要已知该微裂隙的压缩系数Cc，而此参数通常难以测量，因此，我们还需要进一步将式(18)与实验可测量的物理量(如岩石压缩系数)联系起来.

设岩石的总孔隙空间Ωp由N组纵横比为αi的微裂隙组成，其中i=1,2,…,N，取Cp(P)为压力P下总孔隙空间的压缩系数，于是有

dΩp(P)/Ωp(P)=-Cp(P)dP,

Ωp(P)=∑idVc(P,αi).

(19)

联立式(14)和式(19)，得到

φc(P)Cp(P)=∑iφi(P)Cc(P,αi),

(20)

式中，φc=Ωp/Ω为微裂隙的总孔隙度，φi=Vc(αi)/Ω为第i组微裂隙的孔隙度，其中Ω表示岩石体积.由于岩石中充满了各种各样孔隙纵横比的微裂隙，因此，式(20)中的求和符号可以转换为积分符号，且积分区间应包含压力P下保持开孔的所有微裂隙的孔隙纵横比.为此，不妨令

φi=c(α)dα,

(21)

则式(20)变为

(22)

式中，α表示保持张开状态微裂隙的最小纵横比；c(α)称为孔隙度分布函数，根据孔隙度与裂隙密度Γ之间的关系，即φ=4παΓ/3，c(α)可以类似地表示为

(23)

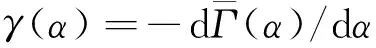
(24)

当微裂隙纵横比较小时，αCc(P,α)与α几乎无关，可以提到积分符号之外.于是，有

(25)

利用式(24)，式(18)可以重新写成

(26)

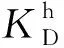
(27)

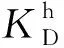
2.2 裂隙密度的理论公式

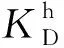
假设岩石仅包含一组纵横比为α=c/a的硬币形微裂隙，其中a和c分别为微裂隙的长轴和短轴，则该组微裂隙的裂隙密度Γ可以表示为

(28)

式中，Ω为岩石体积；L为岩石中微裂隙的数量.于是，微裂隙的总孔隙度φc可以写成

(29)

对于纵横比较小的硬币形微裂隙，其几何因数P和Q具有显式解析表达式(David and Zimmerman, 2011)：

(30)

(31)

式中，ν为岩石基质的泊松比，而岩石基质的选取与等效介质理论有关，比如，对于KT模型和MT模型，ν表示背景基质的泊松比，而对于DEM模型和SCA模型，ν则表示DEM或SCA等效介质的泊松比.另外，由式(29)—(31)可以发现，φP和φQ与α无关，且均为裂隙密度Γ的函数.由此可见，将φP和φQ引入等效介质模型中便可以将岩石弹性模量与裂隙密度Γ联系起来.

对于KT模型，我们可以将φP和φQ代入式(3)中得到裂隙密度的计算公式：

(32)

式中，Kb，Gb和νb分别表示背景基质的体积模量、剪切模量和泊松比.注意，这里的背景基质可以是等效矿物基质m，也可以是其它等效介质，其选择视具体问题而定.

对于MT模型，将φP和φQ代入式(6)中得到

(33)

考虑到微裂隙孔隙度φc≪1，我们在上述公式中运用了近似关系1-φc≈1.

对于DEM模型，David和Zimmerman(2011)推导了如下裂隙密度的解析近似式：

(34)

此近似式的精度略依赖于泊松比vb，但在裂缝密度很高的情况下，其计算误差仍小于2%(David and Zimmerman, 2011).

对于SCA模型，将φP和φQ代入式(12)中有

(35)

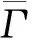
3 基于虚拟降压的反演策略

3.1 微裂隙的压力响应描述

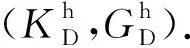
设岩石中所有的微裂隙在压力Pc下刚好全部闭合，且压力区间[0,Pc]由相等的N个子区间和N+1个压力点构成，其中压力点包括0,ΔP,2ΔP,…,NΔP，此处ΔP=Pc/N表示压力增量.假设岩石中N组微裂隙的闭合压力刚好为p1=ΔP,p2=2ΔP,…,pN=NΔP，且ΔP足够小时，各压力子区间内的孔隙纵横比可以认为是恒定的.当有效压力Pe∈[pi,pi+1)时，岩石中初始孔隙纵横比小于α0(pi+1)的所有微裂隙全部闭合，而α0>α0(pi)的微裂隙仍处于张开状态.由式(16)—(17)可知，当压力增加ΔP时，所有微裂隙的纵横比变化量是相同的，这意味着，在压力Pe下岩石中仍处于开孔状态的各组微裂隙的孔隙纵横比均应相对于其初始值减小α0(pi).此时，各组开孔微裂隙的孔隙纵横比应为

α0(pi+1)-α0(pi),α0(pi+2)-α0(pi),…,α0(pN)-α0(pi),

(36)

图3展示了不同压力下岩石中各组微裂隙的开孔情况：当实验压力为0时，所有微裂隙均处于初始状态；当实验压力增至p1，初始纵横比小于或等于α0(p1)的微裂隙闭合，而其它微裂隙的纵横比均减小α0(p1)；当实验压力继续增至p2，满足α0≤α0(p2)的微裂隙全部闭合，而仍处于开孔状态微裂隙的纵横比相对于其初始值减小α0(p2)；以此类推下去，当实验压力增至压力Pc=NΔP时，岩石中的所有微裂隙全部闭合.由此可见，一旦获得各组微裂隙的初始纵横比(即微裂隙的初始纵横比分布)，利用上述过程便能求出不同压力下岩石的微裂隙纵横比分布.

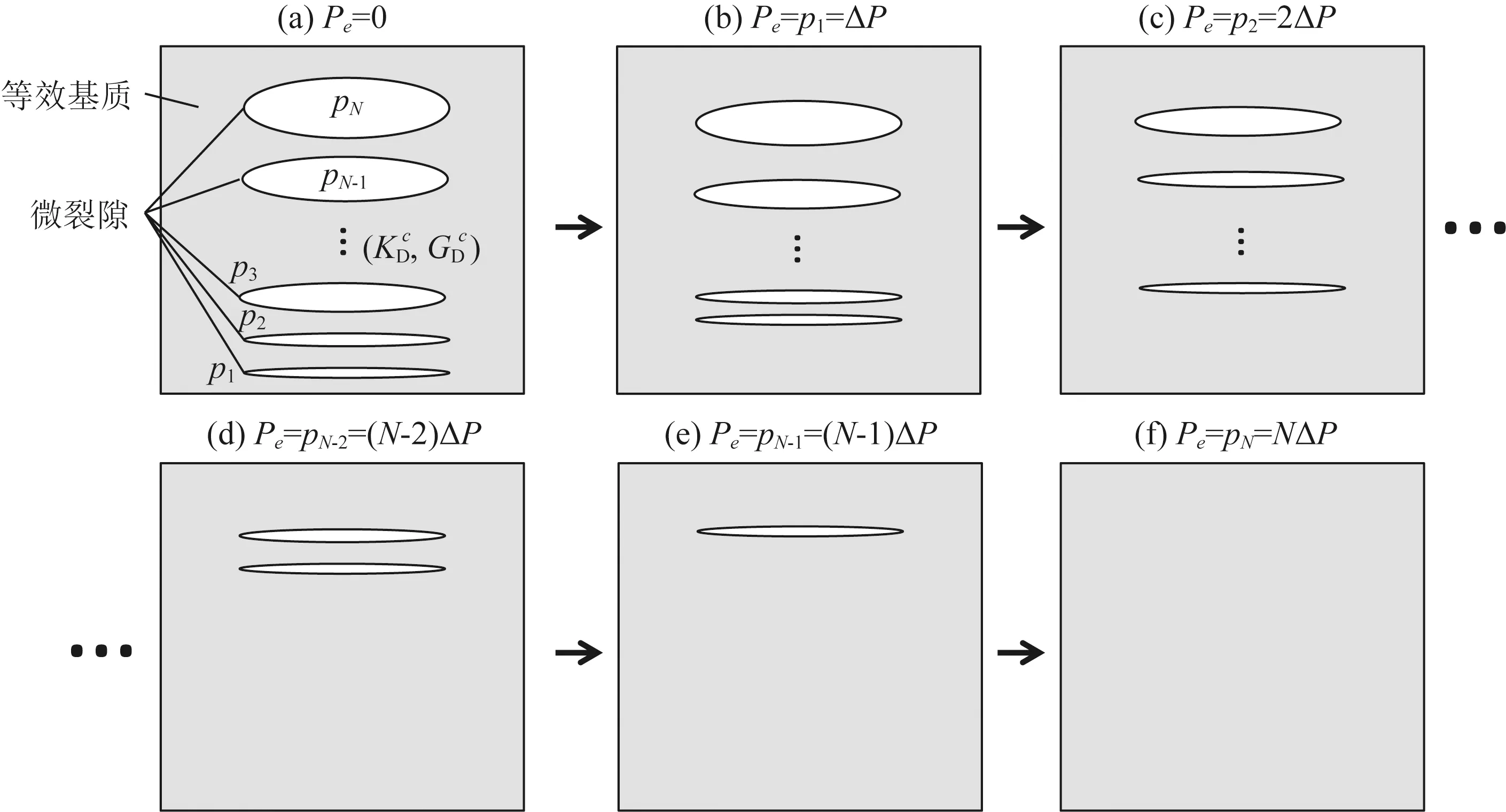
图3 增压过程中岩石内各组微裂隙的形态变化示意图Fig.3 The change of each group of micro-cracks in rock during pressure increasing

3.2 孔隙纵横比反演流程

为了获得微裂隙的初始纵横比，首先需要求解微裂隙的累积裂隙密度(见式(27))，这里我们借助假想降压过程进行计算.注意，这里的假想降压过程是指增压逆过程，即对应于图3中由右往左、由下至上的过程，而并不等同于实际降压过程.事实上，吴春燕等(2016)的实验研究表明，在实际降压过程中岩石孔隙空间通常难以恢复到原始状态.

基于虚拟降压的反演流程主要包括三部分，即微裂隙的累积裂隙密度反演、微裂隙孔隙纵横比分布计算以及硬孔纵横比反演，工作流程见图4.

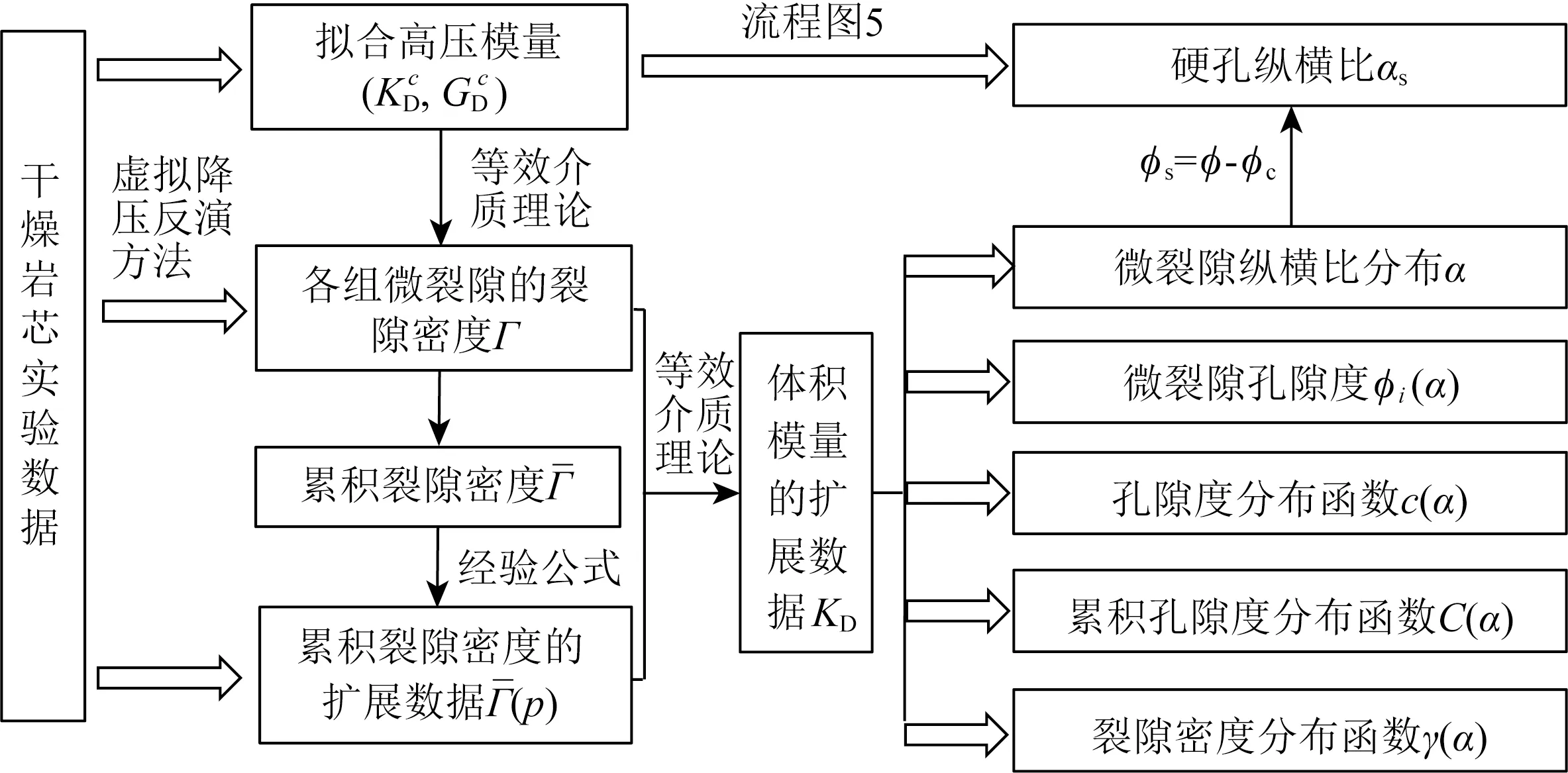
图4 基于虚拟降压的孔隙纵横比反演流程图Fig.4 Inversion workflow of aspect ratio distribution based on a thought unloading method

(1)累积裂隙密度反演

根据假想降压思路，我们将降压过程分为N个变化状态，即pN→pN-1,…,p2→p1,p1→0，其中pN等于最高实验压力Pc.在每个变化状态，干燥岩石均可以视为单重孔隙结构.这意味着，我们可以直接运用第2.2节推导的单重孔隙岩石的等效介质理论公式(32)—(35)计算微裂隙的裂隙密度，具体过程如下：

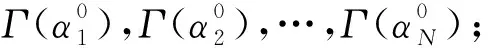
④ 利用各组微裂隙的裂隙密度计算累积裂隙密度：

(37)

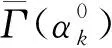
在上述过程中，我们自然而然地认为实验压力点是等间隔分布的.然而，在很多情况下，实际数据并不满足这些要求，此时我们可以利用关系式(13)对实验数据点进行拟合，然后利用扩展后的数据完成上述过程.

(38)

(2)孔隙纵横比分布函数计算

(39)

(40)

(41)

φi(α0)=c(α0)dα0.

(42)

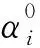
(43)

由此可见，对于α0>α0(pi)的微裂隙，其压力Pe下的裂隙密度分布函数与初始分布函数γ(α0)相同，其原因在于：裂隙密度只与长轴a有关(见式(28))，而a不随压力变化，这意味着在微裂隙没有完全闭合的情况下，其裂隙密度不随外部压力而改变，而只有当微裂隙完全闭合后，该微裂隙对岩石裂隙密度的贡献方降为零.

一般而言，压力对岩石体积Ω的影响可以忽略不计，因此由微裂隙孔隙度的定义φi=4πa3α/(3Ω)可知，孔隙度φi与纵横比α的比值等于常量.于是，在有效压力Pe下，φi(α)可由初始孔隙纵横比α0和初始孔隙度分布函数φi(α0)表示为

φi(α)=φi(α0)α/α0,

(44)

此外，联立式(41)、式(42)和式(44)还可以求出有效压力Pe下的孔隙度分布函数c(α)以及累积孔隙度分布函数C(α).

(3)硬孔纵横比反演

硬孔纵横比反演是基于高压状态下的实验数据实现的.在高压条件下，干燥岩石可以视为由等效矿物基质和单重硬孔构成的两相混合物(见图2d)，此时利用等效介质理论便可以从高压数据中提取出硬孔纵横比.图5给出了硬孔纵横比的反演流程，具体步骤如下：

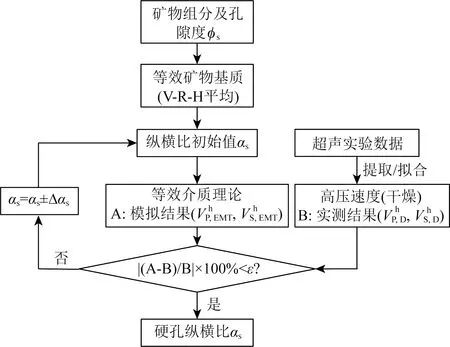
图5 硬孔纵横比反演流程图Fig.5 Inversion workflow for aspect ratio of the stiff pores

① 获取岩芯样品的基本信息，包括样品的总孔隙度φ、矿物组分及其含量、干燥岩石的密度ρD以及各有效压力下的超声纵横波速度VP,D(P)和VS,D(P)，并根据反演得到的微裂隙的总孔隙度φc，计算硬孔的孔隙度φs=φ-φc.对于φc≪φs的情况，也可以由φs≈φ来估算硬孔的孔隙度；

② 利用Voigt-Reuss-Hill平均公式(简称V-R-H平均)计算等效矿物基质模量(Km,Gm)，即(Mavko et al., 2009)

(45)

式中，fi为各矿物组分的体积含量；Mi表示各矿物组分的体积模量或剪切模量.

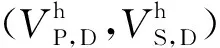
(46)

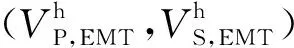
4 实际应用分析

为了分析上述反演流程的可靠性和适用性，我们分别选取了具有代表性的2块砂岩样品S1和S2与2块致密碳酸盐岩样品C1和C2，并采用基于虚拟降压的反演方法对其孔隙结构参数进行了提取.表1列出了这些岩芯样品的基本参数和数据来源，其中样品S1为纯石英砂岩，孔隙度为4%，岩芯数据来自于文献David (2012)；样品S2为泥质砂岩，孔隙度为23.9%，主要矿物成分为石英(66%)、长石(17%)、粘土(15%)以及极少量的黄铁矿和菱铁矿，其孔隙结构特征见图6(a—b)；样品C1和C2为纯净的致密碳酸盐岩，孔隙度分别为3%和0.6%，其矿物基质均由100%的方解石构成，两块碳酸盐岩样品均为致密灰岩，其中样品C1主要发育晶间孔和粒内孔，而样品C2具有较强的非均质特征，孔隙以局部发育的平直微裂缝为主，孔隙结构特征见图6(c—f).

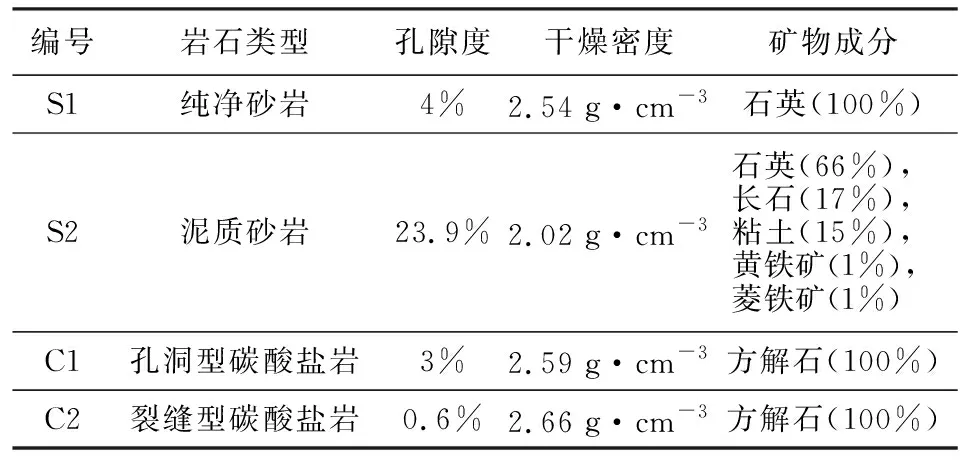
表1 砂岩和碳酸盐岩样品的基本参数Table 1 Physical properties of the sandstone and carbonate samples

图7 干燥岩芯样品的纵横波速度-压力曲线(a) 纯净砂岩样品S1; (b) 泥质砂岩样品S2； (c) 孔洞型致密碳酸盐岩样品C1； (d) 裂缝型致密碳酸盐岩样品C2.Fig.7 Velocity versus confining pressure for dry rock samples(a) Pure sandstone sample S1； (b) Shaley sandstone sample S2; (c) Tight carbonate sample C1 with inter-granular pores； (d) Tight carbonate sample C2 with cracks.

图7给出了不同实验压力下干燥砂岩样品S1，S2与碳酸盐岩样品C1，C2的纵横波速度超声实验测量结果.由图7可见，砂岩样品和碳酸盐岩样品对压力的弹性响应存在显著差异.当有效压力由0 MPa增至20 MPa时，砂岩样品的纵横波速度迅速增大；但随着有效压力的继续增大，其纵横波速度的增长趋势逐渐减缓，达到最大值后趋于平稳.这表明砂岩样品中存在大量小纵横比的微裂隙(如粒间孔)以及少量纵横比较大的微裂隙，由于小纵横比微裂隙的闭合压力较小且数量极多，所以当压力略微增加时大量的微裂隙闭合，从而使岩石的纵横波速度迅速增加.从图7a—b可以推测出，砂岩样品中的大部分微裂隙在有效压力到达20 MPa时便已全部闭合，而仅剩余少数纵横比较大的微孔处于开孔状态；当压力继续增大并超过剩余微孔的闭合压力后，这些纵横比较大的孔隙才相继闭合，但由于其数量较少，岩石速度随压力的增加趋势也逐渐减缓.对于致密碳酸盐岩样品而言，纵横波速度随压力的变化则相对平缓(见图7c—d).这意味着，与小纵横比微裂隙占主导的砂岩样品相比，碳酸盐岩样品中各种微裂隙的数量差异相对较小.因此，在有效压力较低的范围内，其纵横波速度随压力的增加趋势也相对平缓.

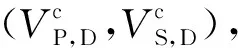
(47)

由表2可见，对于纯净砂岩样品S1和非均质程度较低的孔洞型碳酸盐岩样品C1，KT、MT、DEM和SCA模型均能取得很好的反演效果，其反演误差均小于0.5%，且这些模型估计的硬孔隙纵横比十分接近(样品S1：～0.4，样品C1：～0.18).对于泥质砂岩样品S2，四种模型的反演精度略低，其中DEM模型的效果最佳，其反演误差为2.05%，KT模型的效果最差，其反演误差为4.31%.由此可见，泥质及其他掺杂矿物对砂岩硬孔纵横比的反演精度影响较大，其原因在于：岩石弹性模量的主要贡献来源于矿物成分，而对于包含有多种矿物组分的非纯净砂岩，V-R-H平均仅能提供一个粗略的等效矿物基质模量估计值，因此存在一定的误差.另外，对于裂缝型碳酸盐岩样品C2，四种等效介质理论的反演结果均不理想，最大反演误差接近5%.由于C2为纯净碳酸盐岩样品，矿物组分的影响几乎可以忽略，因此，该误差主要来源于碳酸盐岩的复杂孔隙结构分布.由图6f可见，样品C2存在局部发育的裂缝，具有较强的非均质性，而本文采用的反演算法理论上更适合非均质性较弱的岩石.

表2 基于不同等效介质理论反演的硬孔隙纵横比Table 2 Inversion results of the characteristic aspect ratio for the stiff pore obtained from different effective medium theories

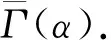
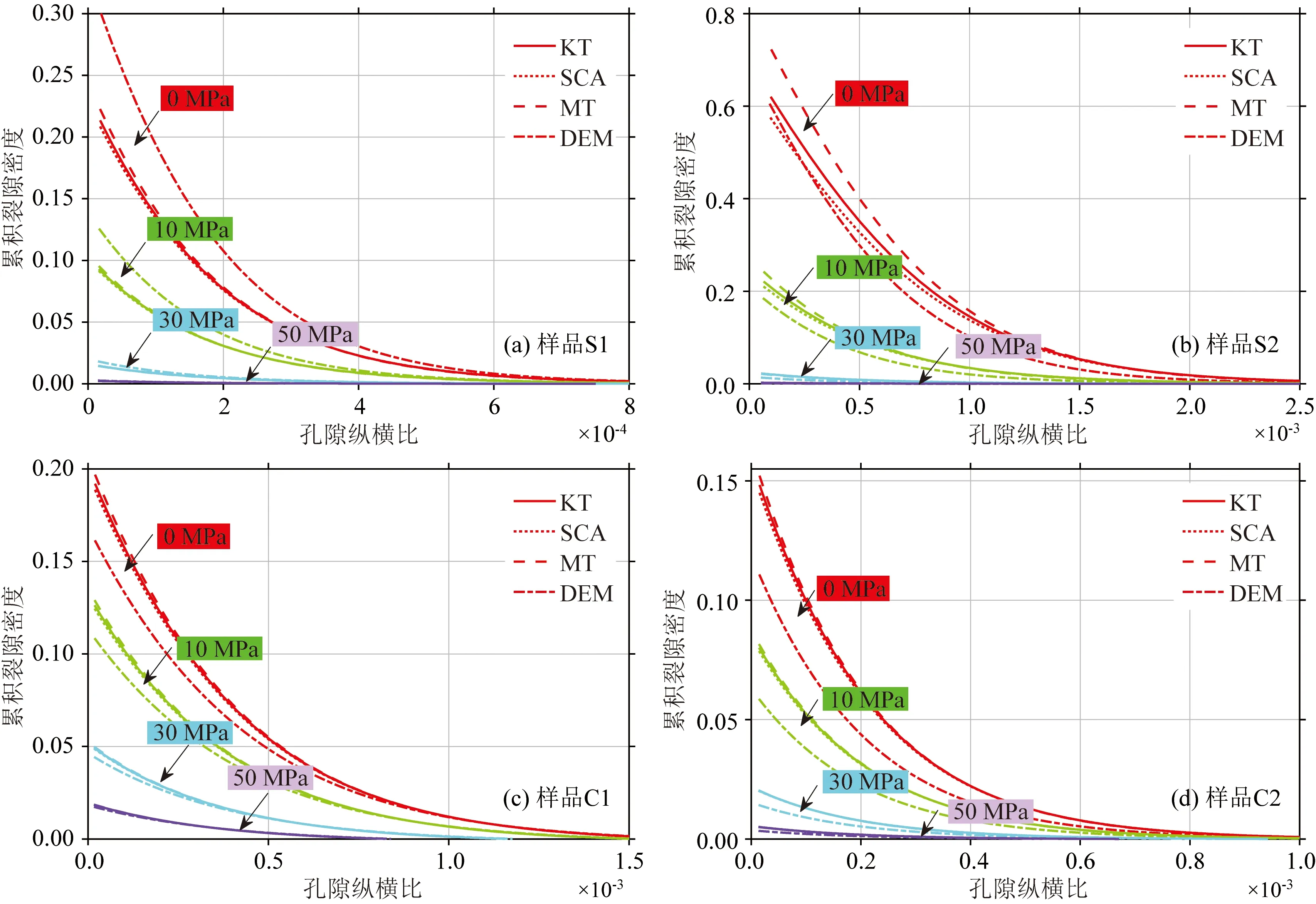
图8 基于4种等效介质理论反演的不同有效压力下砂岩(a—b)和碳酸盐岩(c—d)样品的累积裂隙密度分布Fig.8 Cumulative crack density distribution as a function of the aspect ratio calculated by different effective medium theories at different pressures for sandstone (a—b) and carbonate samples (c—d)

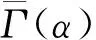
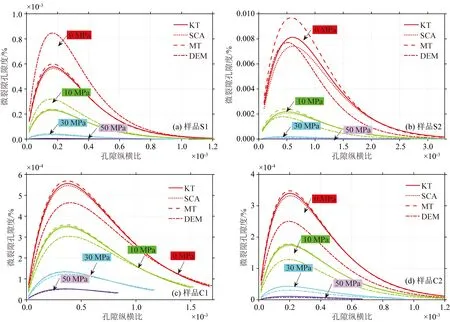
图9 基于4种等效介质理论反演的不同有效压力下砂岩(a—b)和碳酸盐岩(c—d)样品的微裂隙孔隙度Fig.9 Crack porosity as a function of the aspect ratio calculated by different effective medium theories at different pressures for sandstone (a—b) and carbonate samples (c—d)

下面我们从数据统计的角度分析四种等效介质理论的反演效果.我们以31块干燥泥质砂岩和40块干燥碳酸盐岩的超声纵横波速度作为输入数据，其中砂岩样品的主要矿物成分为石英、长石、方解石、白云石和粘土，孔隙度分布范围为3.5%～30%；碳酸盐岩样品主要由方解石构成，其孔隙度分布范围为0.3%～3% .图10给出了四种理论的模拟结果及超声实验数据.从图中可以看出，无论是泥质砂岩还是碳酸盐岩，四种等效介质理论的模拟速度与实测速度均具有很好的一致性.结合图8和图9可见，这些理论的反演精度和反演结果均十分接近.由此可见，本文提出的孔隙结构反演方法并不十分依赖于等效介质理论的选择，四种等效介质理论均能作为反演孔隙结构参数的有效工具.但是，在计算效率方面，由于KT和MT模型具有显式的理论表达式，其计算速度比隐式的DEM和SCA模型更快.

为了对比本文方法与现有方法，我们采用基于虚拟降压的反演方法(见第4.2节)和D-Z方法(Zimmerman, 1999; David and Zimmerman, 2012;邓继新等, 2015)计算了不同有效压力下干燥岩石的弹性模量，以此评估两种方法的反演精度.本文方法与D-Z方法的主要区别在于，D-Z方法直接采用单重孔隙岩石的裂隙密度公式(式(33)和式(34))近似反演多重孔隙岩石的累积裂隙密度；而本文方法则借助假想降压过程实现多重孔隙岩石的累积裂隙密度计算.以DEM模型为例，图11和图12分别从单块岩芯与统计分析的角度对比了两种方法的反演结果.由图11可见，对于纯净砂岩样品S1，本文方法和D-Z方法均能取得很好的反演效果；但对于泥质砂岩和碳酸盐岩，由D-Z方法计算的体积模量与实测数据存在较大误差，且计算误差随着有效压力的减小而增大，这表明D-Z模型所采用的近似做法(即直接利用单重孔隙公式(33)—(34)近似计算多重孔隙岩石的累积裂隙密度)存在一定局限性.另一方面，从图11—12中可以看出，本文方法相较于D-Z方法具有更高的精度，无论是砂岩还是碳酸盐岩，由本文方法计算得到的体积模量和剪切模量与实际数据吻合更好.由此可见，本文方法比D-Z方法更具优势，能够有效克服经典D-Z反演方法的精度不足.

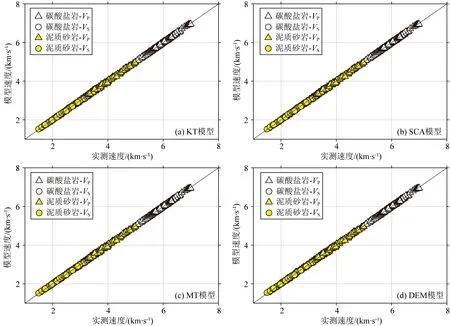
图10 基于不同等效介质理论的模型反演结果与实际测量结果对比Fig.10 Comparison of the measured velocities and the results inverted using different effective medium theories

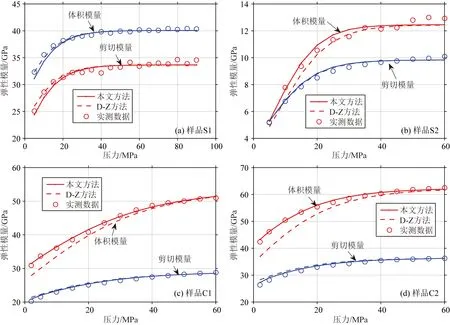
图11 本文方法和D-Z方法基于DEM理论反演的干燥岩石弹性模量对比(a) 纯净砂岩样品S1; (b) 泥质砂岩样品S2； (c) 孔洞型致密碳酸盐岩样品C1； (d) 裂缝型致密碳酸盐岩样品C2.Fig.11 Elastic Moduli of dry rock calculated with DEM by using our method and D-Z method(a) Pure sandstone sample S1； (b) Shaley sandstone sample S2; (c) Tight carbonate sample C1 with inter-granular pores； (d) Tight carbonate sample C2 with cracks.

图12 本文方法和D-Z模型反演结果对比Fig.12 Comparison of our method and D-Z method

5 结论

本文对经典D-Z方法进行了改进和完善，并将其推广至KT、MT、DEM和SCA四种等效介质模型的情形，建立了一套完整的孔隙纵横比反演流程.以一系列砂岩样品和碳酸盐岩样品为例，分析了本文方法在实际岩芯孔隙纵横比提取中的应用效果，数值分析结果表明：基于本文方法从干燥岩芯速度-压力数据中提取的孔隙纵横比分布、累积裂隙密度分布和微裂隙孔隙度分布可以很好地解释实际岩芯中微裂隙的压力响应规律；此外，本文方法并不十分依赖于等效介质理论的选择，即四种理论均能取得十分好的反演精度，且反演的孔隙结构参数差异很小；与经典D-Z方法相比，本文方法有效改善了D-Z方法中利用单重孔隙公式近似计算多重孔隙岩石累积裂隙密度所引起的精度不足.在实际应用方面，本文所建立的反演流程可以为岩石物理实验和理论研究提供重要的孔隙结构参数提取工具；另外，结合深度和压力的对应关系，此方法也有望应用于测井数据的岩石孔隙结构参数反演中.

附录A 椭球状孔隙的几何因数

对于纵横比小于1的椭球状孔隙，其几何因数P和Q可以表示为(Mavko et al.，2009)

×(F2F4)-1],

式中，

F1=1+A[1.5(fi+θi)-R(1.5fi+2.5θi-4/3)],

F2=1+A[1+1.5(fi+θi)-0.5R(3fi+5θi)]

+B(3-4R)+0.5A(A+3B)(3-4R)[fi+

F3=1+A[1-(fi+1.5θi)+R(fi+θi)],

F4=1+0.25A[fi+3θi-R(fi-θi)],

F5=A[-fi+R(fi+θi-4/3)]+Bθi(3-4R),

F6=1+A[1+fi-R(fi+θi)]

+B(1-θi)(3-4R),

F7=2+0.25A[3fi+9θi-R(3fi+5θi)]

+Bθi(3-4R),

F8=A[1-2R+0.5fi(R-1)+0.5θi(5R-3)]

+B(1-θi)(3-4R),

F9=A[(R-1)fi-Rθi]+Bθi(3-4R),

其中：

A=Gi/Gm-1,

R=(Km/Gm+4/3)-1

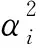
附录B DEM解析近似式的系数

在DEM的解析近似式中，a,b,S0i,S1i,S2i和S3i的具体表达式分别为

S1i=(θi-fi)/(2-3fi-3θi),

S2i=4/3,

式中，

-0.2F2F4(F′4F5+F4F′5+F′6F7+F6F′7

F′1=-A(1.5fi+2.5θi-4/3)R′,

F′2={-0.5A(3fi+5θi)-4B-0.5A(A+3B)

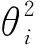
F′3=A(fi+θi)R′,

F′4=-0.25A(fi-θi)R′,

F′5=[A(fi+θi-4/3)-4Bθi]R′,

F′6=[-A(fi+θi)-4B(1-θi)]R′,

F′7=[-0.25A(3fi+5θi)-4Bθi]R′,

F′8=[A(-2+0.5fi+2.5θi)-4B(1-θi)]R′,

F′9=[A(fi-θi)-4Bθi]R′,

R′=-R2.