极地海洋工程装备平板构件的对流换热影响分析

操太春 吴刚 孔祥逸 于东玮 吴琳 张大勇

研究论文

极地海洋工程装备平板构件的对流换热影响分析

操太春1,3吴刚2孔祥逸1于东玮1,3吴琳1张大勇1

(1大连理工大学海洋科学与技术学院, 辽宁 盘锦 124221;2中国船舶工业集团公司第七○八研究所, 上海 200021;3大连理工大学运载工程与力学学部, 辽宁 大连 116023)

电伴热是极地海洋工程装备防寒主要措施, 热平衡是对流换热的关键问题。本文以平板构件为研究对象, 采用数值模拟和模型试验相结合的方法, 开展极地复杂环境因素对海洋工程装备电加热平板构件热平衡影响分析。首先选取风速、温度为主要环境参数, 风速为0～40m·s–1、温度为–40～0℃, 基于Fluent仿真和试验测试获得电加热平板构件在不同风速、温度下的对流换热系数。结果表明: 增大风速和降低温度都会使平板的对流换热系数增大, 在风速一定的情况下, 温度对平板的换热影响较小; 在温度一定的情况下, 平板的对流换热系数随着风速的增加而显著增大。最后, 基于试验数据建立了电加热平板构件的对流换热系数数学预测模型, 并采用数值模拟验证了该模型的正确性。

极地 平板构件 对流换热 实验测试 数值模拟

0 引言

极地海洋工程装备是极地资源探测开发的主要载体, 然而受极端低温、潮湿环境影响, 装备极易发生结冰现象。结冰增加的重量不仅会降低结构稳定性、改变结构应力, 还可能影响工程设备的正常运行[1]。平板构件作为极地海洋工程装备中的典型构件, 例如甲板、舱壁等, 其防寒措施一般采用伴热方式。

伴热有两类加热方式, 分别为恒壁温加热和恒热流加热。恒壁温加热的壁面温度保持恒定; 恒热流加热以恒定的热流量输入, 当没有热量损失时, 壁面温度将持续升高。因此这两种加热方式存在较大差别, 而极地工程装备的电伴热属于恒热流加热。目前, 极区海洋工程装备的防寒设计普遍参考船级社的相关规范[2], 由于对工程环境条件考虑较少[3], 实际运行过程中存在电伴热的给热量不合理问题[4-6], 在保证防寒效果的同时极易造成加热能量的浪费, 给极地工程装备的电力系统造成额外负担。

目前, 平板的热平衡研究主要集中在恒壁温加热, Churchill[7]基于理论和实验分析, 提出了恒壁温加热条件下平板的平均努塞尔数()、局部关于普朗特数()与雷诺数()的表达式, 并明确各参数的取值。Junkhan等[8]研究了不同压力梯度下湍流度对平板换热的影响, 在层流换热范围内主流中湍流的作用不大, 但在湍流换热范围内, 传热系数随湍流度的增大而增大。Whitaker[9]对层流边界层及湍流边界层的局部表达式进行了修正, 确定了平均; 研究发现采用简单的函数关系来描述平板的对流换热过程会存在一定误差。Luikov等[10]研究了平板在恒壁温条件下的边界层及热量交换机制, 给出了低普朗特数、速度分布和温度分布的解析解。

然而, 极地装备保温系统采用的电加热属于恒热流加热方式, 现阶段, 平板构件在电加热条件下的对流换热研究相对缺乏。Treviño等[11]研究了平板在对流条件下的稳态和瞬态加热过程, 得到了平板在恒热流加热条件下纵向位置的温度变化规律。Brazil等[5]研究了平板在不同温度、不同风速下的热量损失, 发现较大的表面积导致的热损失超过船级社规范近50%。因此, 对于极地海洋工程装备的防寒系统的设计不能完全参照船级社的规范, 同时应该考虑外部环境变化所带来的影响。张雷等[12]对船舶在极区的运行工况进行研究, 分析了甲板除冰系统设计要点、计算方法以及相关的规范, 提出了极地船甲板除冰系统的设计方法。

可见, 加热方式对平板构件的对流换热影响显著, 目前电加热方式下的换热规律还不是很明确, 理论计算还存在较大误差。因此, 亟需建立平板构件的对流换热系数预测模型, 为极地海洋工程装备防寒设计提供参考。本文采用实验结合Fluent仿真的方法, 对电加热平板构件的对流换热进行了研究分析。实验研究了温度范围–40～0℃、风速范围0～13.7 m·s–1的对流换热系数随温度以及风速的变化规律, 并提出了对流换热系数的拟合计算公式。通过数值仿真验证了拟合公式在温度范围–40～0℃、风速范围0～40m·s–1内的适用性。

1 平板的对流换热要素分析

由牛顿冷却公式可知, 平板的局部对流换热系数可以表示为:

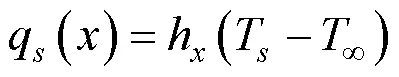
电加热条件下, 平板的热流通量是给定的额定量, 此时壁面温度分布为[13]:

对于层流段

对于湍流段

层流段局部表面传热系数

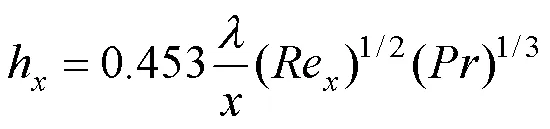
湍流段局部表面传热系数

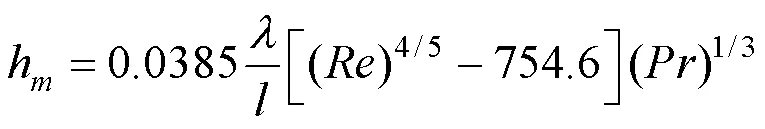
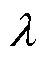
2 电加热平板的对流换热实验

在低温实验室, 搭建了面向极地环境条件下的海洋工程装备平板构件对流换热实验平台, 实现了平板构件在不同风速、温度条件下对流换热系数的准确测定。低温实验室可控调节最低温度为–50℃, 最大风速为15 m·s–1, 基本可以模拟极地的低温环境。平板的对流换热涉及层流段、过渡段和湍流段, 为充分考虑对流换热不同阶段产生的影响, 实验选取的平板构件长2.4 m、宽0.7 m。

2.1 实验系统

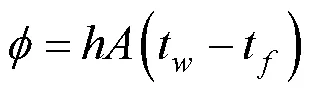
由此可得,

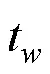
2.2 实验结果分析

在低温实验室进行了24组平板对流换热实验, 实验工况设置及实验结果如表2所示。

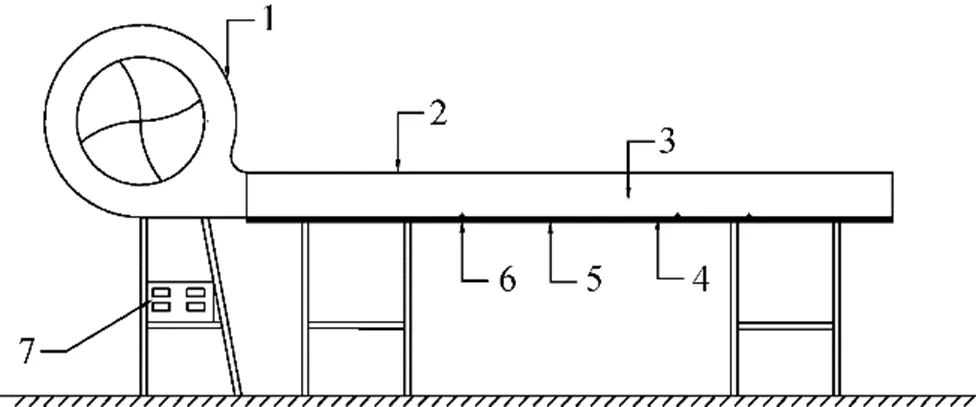
图1 实验装置.1: 变频风机, 2: 风罩, 3: 风道, 4: 实验平板, 5: 加热丝及保温层, 6: 实验平板上的测点, 7: 控制箱

Fig.1.Experimental apparatus.1: converter fan, 2: air hood, 3: air flow tunnel, 4: experimental plate, 5: heating wire and insulation layer, 6: measuring points on experimental plate, 7: control box

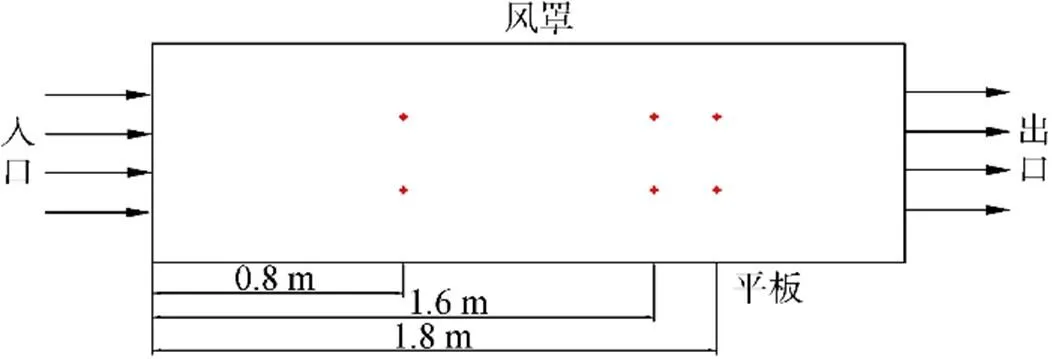
图2 测点位置布置图

Fig.2.Arrangement of measurement location

表1 实验测量装置

对流换热系数的实测值误差主要包含两方面。(1)实验测量的平板温度和风温在±0.1℃范围内波动, 测量温度的PT100传感器的精度为±0.1℃。(2)实验数据的处理方法：为减小实验测量误差, 每组实验工况进行3次，考虑过渡段的影响, 数据处理时取整个平板的平均温度计算对流换热系数。

选取风速相近的实验测量数据进行温度对换热系数的影响分析, 其结果如图3所示。由图可知, 平板对流换热系数实测结果大于理论计算值, 在温度为–20℃左右时, 实测值比其他温度下的实测值偏小, 主要原因为该温度下的实验风速相对较小, 对流换热系数随温度变化影响很小。可以认为, 在风速一定的情况下, 温度对平板的换热基本没有影响。

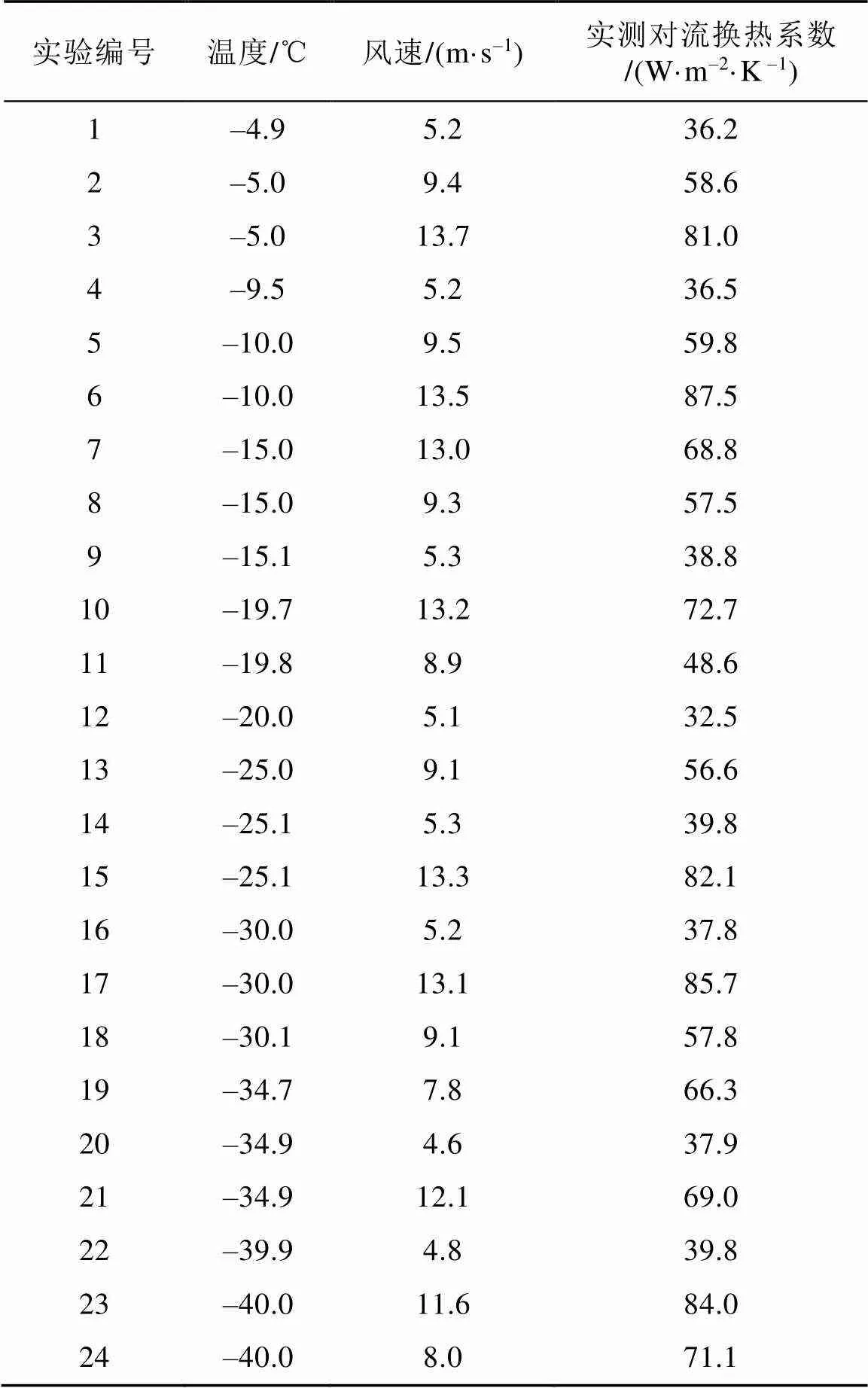
表2 实验工况及结果

为了明确风速对平板对流换热的影响, 本文将温度较为接近的实验工况下实测数据对比分析, 平板对流换热系数随着温度变化情况如图4所示。由图可知, 平板对流换热系数实测结果大于理论值, 在温度一定的情况下, 平板的对流换热系数随着风速的增加而显著增大, 可以认为在特定温度下, 风速是影响平板换热的主要因素。

2.3 基于实验的平板对流换热系数预测模型

从以上分析发现, 加热平板对流换热系数的实验结果要大于理论值, 在一定程度上说明理论推导过程中只考虑层流段和湍流段的换热是不合理的, 过渡段的影响不可忽视[14]。温度一定时, 平板的对流换热系数在风速范围4.6～9.5 m·s–1内平均增大60.3%, 在风速范围9.5～13.7m·s–1内平均增大45.4%; 风速一定时, 在温度范围–30～0℃内平均增大4.4%, 在温度范围–40～30℃内平均增大5.0%。因此, 风速是影响平板换热的主要因素, 温度对其影响很小, 受温度影响的相关参数的变化范围如表3所示。

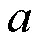
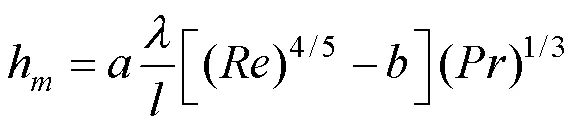
Fig.3.Variation of convective heat transfer coefficient with temperature.a) wind speed at 5.1–5.3 m·s–1; b) wind speed at 8.9– 9.5 m·s–1

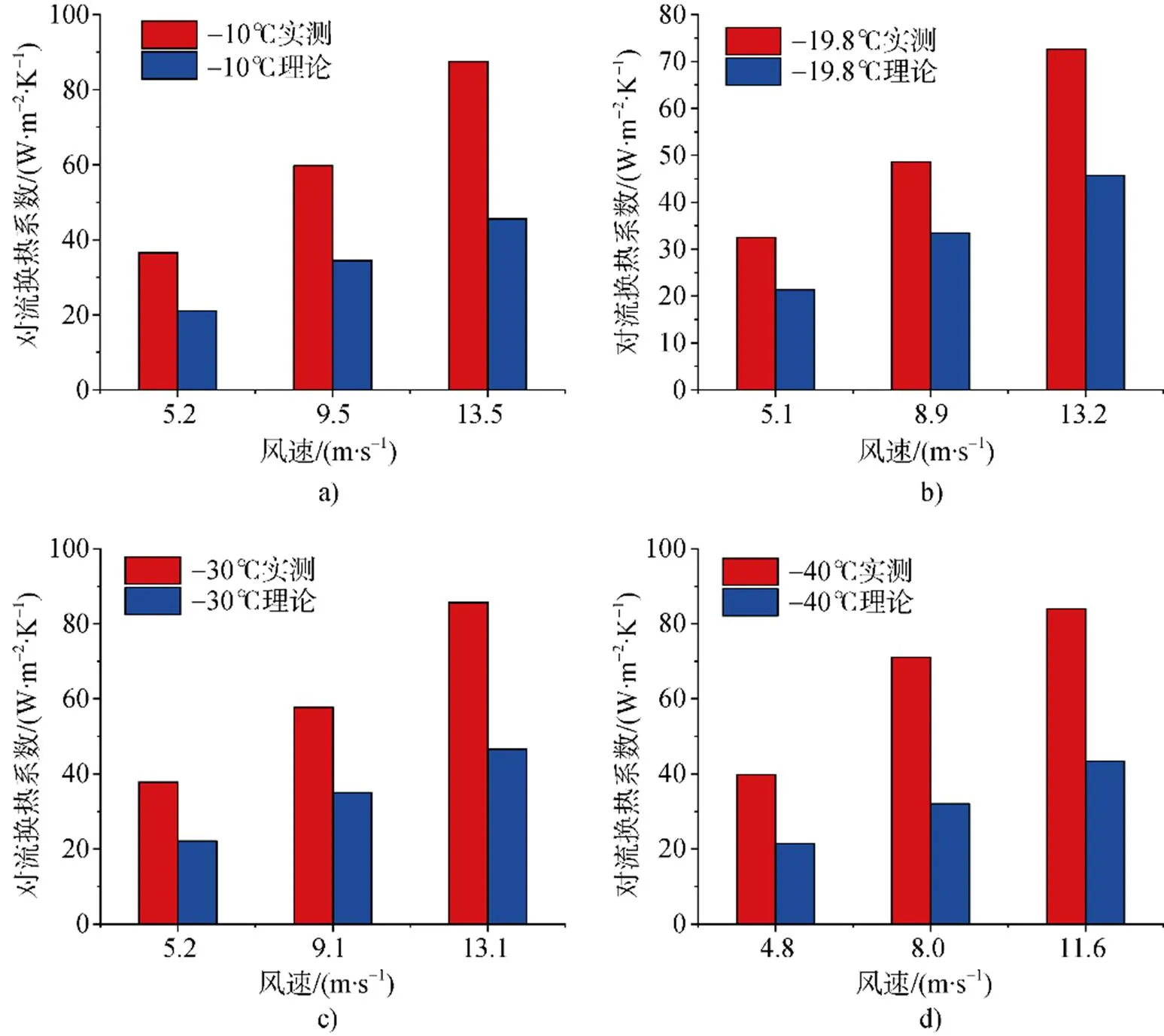
图4 对流换热系数随着风速变化情况。a) 温度为–10℃; b) 温度为–19.8℃; c) 温度为–30℃; d) 温度为–40℃

Fig.4.Variation of convective heat transfer coefficient with wind speed.a) temperature at –10℃; b) temperature at –19.8℃; c) temperature at –30℃; d) temperature at –40℃

表3 普朗特数(Pr)与导热系数(λ)的范围

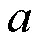
图6比较了拟合公式与实测值的结果: 风速在5 m·s–1以及9 m·s–1左右时, 拟合公式和实测结果能够非常好地接近, 其平均误差为4.7%; 风速在13 m·s–1左右时, 误差为6.0%, 验证了拟合结果的正确性。

3 对流换热系数的数值分析

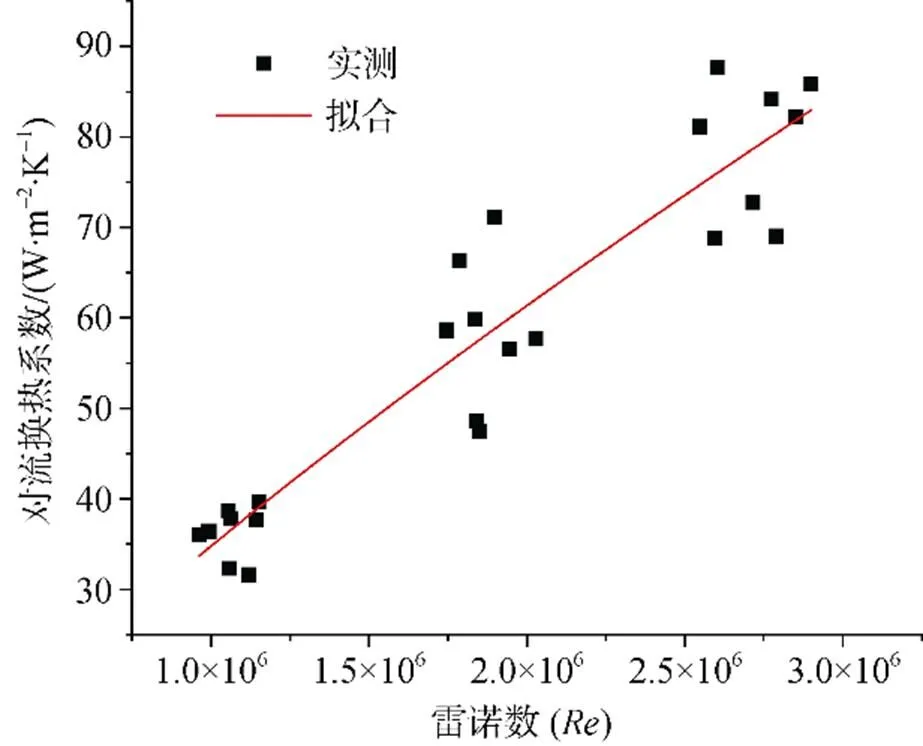
图5 对流换热系数实测数据拟合

Fig.5.Fitting of the measured data of convective heat transfer coefficients

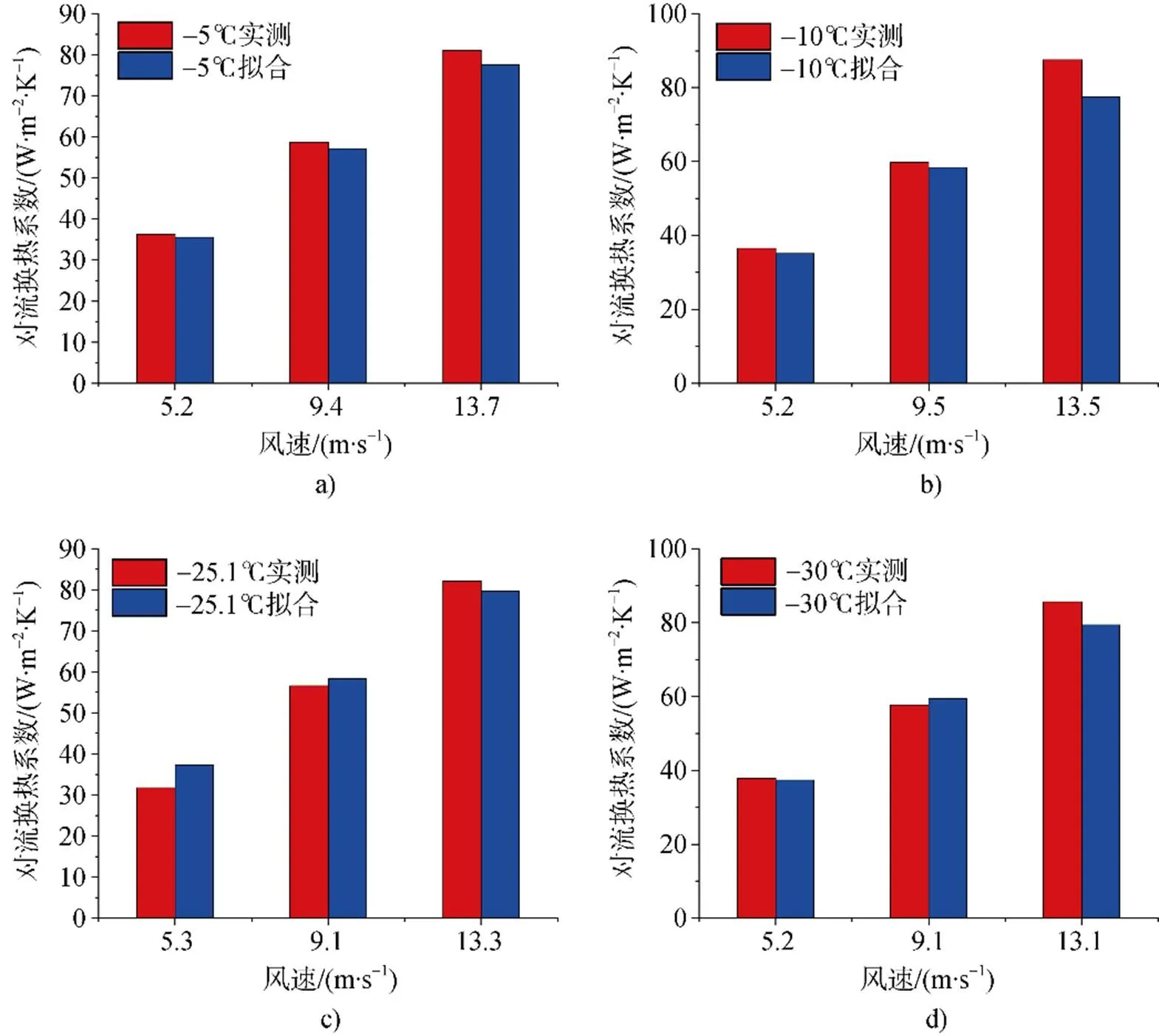
图6 拟合与实测结果对比.a) 温度为–5℃; b) 温度为–10℃; c) 温度为–25.1℃; d) 温度为–30℃

Fig.6.Comparison between fitting and measured results.a) temperature at –5℃; b) temperature at –10℃; c) temperature at –25.1℃; d) temperature at –30℃

3.1 风速和温度的影响分析

加热平板对流换热系数随风速和温度的变化如图7和图8所示。由图7可知, 增大风速和降低温度都会使平板的对流换热系数增大, 并且风速比温度对平板的对流换热影响更加显著。在风速小于25 m·s–1时, 温度对平板的对流换热系数影响很小; 当风速大于25 m·s–1时, 温度对平板的对流换热系数影响增大。由图8可知, 温差一定时, 不同风速下对流换热系数增幅不同。风速大于25 m·s–1时, 对流换热系数随温度变化的曲线斜率变大, 说明温度对平板的对流换热系数影响加大。

3.2 数值仿真与预测模型的对比分析

预测模型与数值仿真结果的对比如图9所示。当风速小于20 m·s–1时, 预测模型与仿真结果吻合度较好, 其平均误差为5.0%, 验证了数值仿真模型的准确性。当风速大于20 m·s–1时, 模型预测值相较数值仿真结果偏大, 平均误差为7.2%,满足工程要求。由温度影响分析可知, 在高风速时温度的影响逐渐变大, 这也在一定程度上解释了拟合结果在高风速时预测模型结果与仿真结果偏差增大。但是误差分析表明在风速范围0～40 m·s–1内, 所得平板对流换热系数预测模型可为海洋工程装备的平板热平衡计算提供参考。

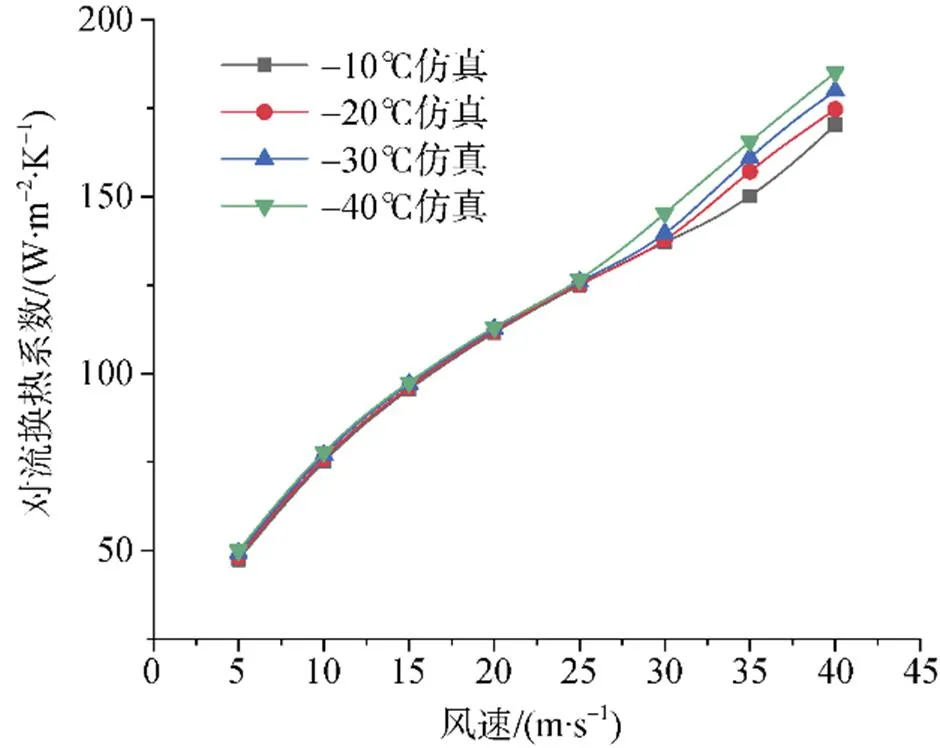
图7 温度–40～0℃下对流换热系数随风速变化

Fig.7.Variation of convective heat transfer coefficient at temperature (–40～0℃) with wind speed

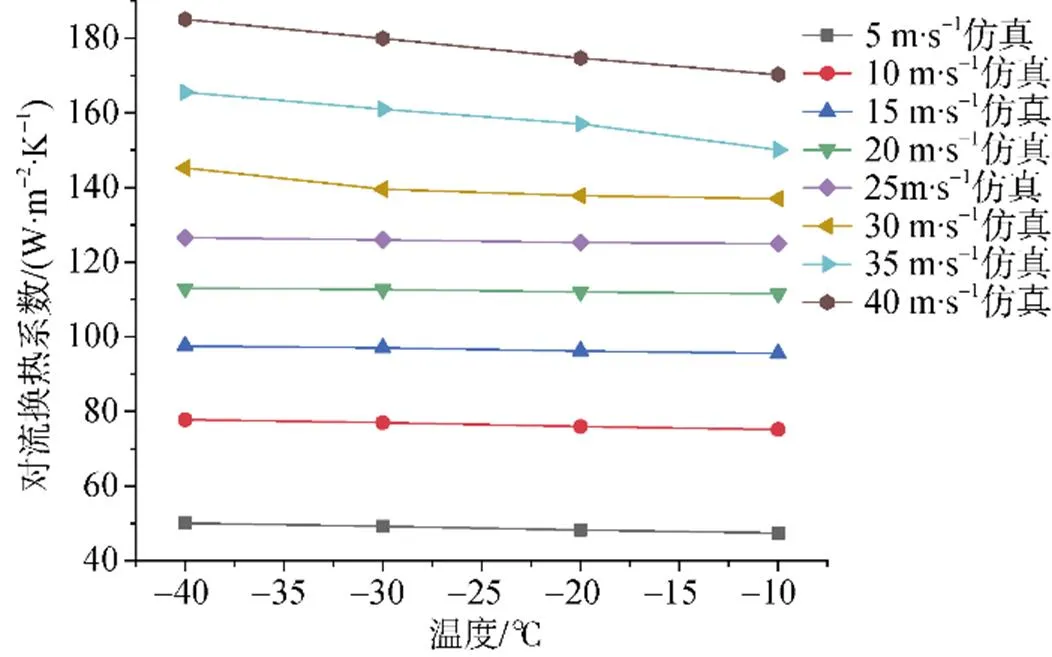
8 风速0～40 m·s–1下对流换热系数随温度变化

Fig.8.Variation of convective heat transfer coefficient at wind speed (0～40 m·s–1) with temperature

4 结论

本文采用实验测试和数值模拟相结合的方法, 对海洋工程装备电加热平板构件热平衡影响分析开展研究。模型实验中, 温度范围为–40～0℃、风速范围为0～13.7 m·s–1, 结果表明: (1)平板对流换热系数的实验结果要大于理论值, 理论推导应该合理地考虑过渡段的影响; (2)增大风速和降低温度都会使电加热平板的对流换热系数增大, 风速的影响更加显著; (3)基于实验获得了平板对流换热系数预测模型。

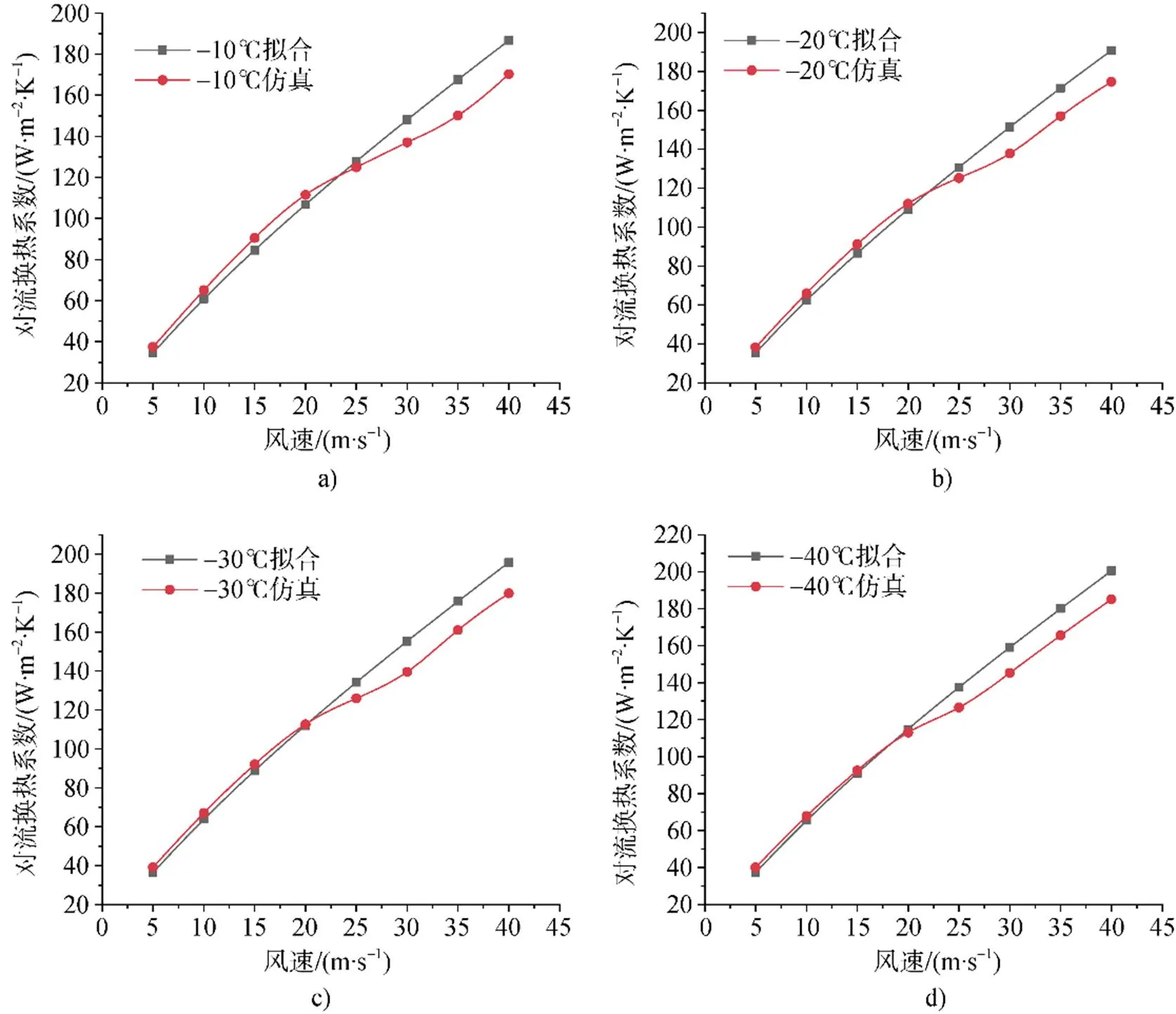
图9 数值仿真与拟合结果对比.a) 温度为–10℃; b) 温度为–20℃; c) 温度为–30℃; d) 温度为–40℃

Fig.9.Comparison of numerical simulation and fitting results.a) temperature at –10℃; b) temperature at –20℃; c) temperature at–30℃; d) temperature –10℃

数值模拟对实验条件不能达到的高风速工况进行了补充, 计算分析了风速在0～40 m·s–1范围内电加热平板的对流换热系数, 结果表明: (1)增大风速和降低温度都会增加平板的对流换热系数, 风速影响显著; (2)在风速小于25 m·s–1时, 温度对平板的对流换热系数影响很小; 当风速大于25 m·s–1时, 温度对平板的对流换热系数影响加大; (3)验证了基于实验获得的对流换热预测模型的适用性。

极地海洋工程装备的构件类型众多, 本文仅以平板构件为例开展电伴热条件下对流换热影响分析, 对于其他构件(例如扶手、踏步等)还需进一步开展研究。

1 沈杰, 白旭.基于Fluent和FENSAP-ICE的极区海洋平台甲板结构结冰数值模拟[J].极地研究, 2020, 32(2): 177-183.

2 陈宪, 汪建华.极地船电加热系统设计[J].广船科技, 2015, 35(5): 5-9.

3 BAEN P, OLDFORD D.Surface heating for Arctic vessels and structures to prevent snow and ice accumulation[C]//2014 Petroleum and Chemical Industry Conference Europe.2014: 1-10.

4 ROEDER W, BAEN P, SEITZ R.Electric trace heat design methods for de-icing and anti-icing of vessels, support equipment and infrastructure in the Arctic[C]//Oceans.IEEE, 2017.

5 BRAZIL H, CONACHEY R, SAVAGE G, et al.Electrical heat tracing for surface heating on arctic vessels and structures to prevent snow and ice accumulation[J].IEEE Transactions on Industry Applications, 2013, 49(6): 2466-2470.

6 RYERSON C C.Ice protection of offshore platforms[J].Cold Regions Science and Technology, 2011, 65(1): 97-110.

7 CHURCHILL S W.A comprehensive correlating equation for forced convection from flat plates[J].AIChE Journal, 1976, 22(2): 264-268.

8 JUNKHAN G H, SEROVY G K.Effects of free-stream turbulence and pressure gradient on flat-plate boundary-layer velocity profiles and on heat transfer[J].Journal of Heat Transfer, 1967, 89(2): 169-175.

9 WHITAKER S.Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles[J].AIChE Journal, 1972, 18(2): 361-371.

10 LUIKOV A V, ALEKSASHENKO V A, ALEKSASHENKO A A.Analytical methods of solution of conjugated problems in convective heat transfer[J].International Journal of Heat and Mass Transfer, 1971, 14(8): 1047-1056.

11 TREVIÑO C, LIÑÁN A.External heating of a flat plate in a convective flow[J].International Journal of Heat and Mass Transfer, 1984, 27(7): 1067-1073.

12 张雷, 伍蓉晖, 陈方红, 等.极地船甲板除冰系统设计[J].广东造船, 2019, 38(1): 58-60.

13 INCROPERA F P, DEWITT D P.Fundamentals of heat and mass transfer[M].5th ed.New York: John Wiley & Sons, 2001: 389-395.

14 LIENHARD J H.Heat transfer in flat-plate boundary layers: A correlation for laminar, transitional, and turbulent flow[J].Journal of Heat Transfer, 2020,142(6):061805.

Analysis on the influence of convective heat transfer of polar ocean engineering equipment plate components

Cao Taichun1,3, Wu Gang2, Kong Xiangyi1, Yu Dongwei1,3, Wu Lin1, Zhang Dayong1

(1College of Marine Science and Technology, Dalian University of Technology, Panjin 124221, China;2Marine Design and Research Institute of China, Shanghai 200021, China;3Department of Carrier Engineering and Mechanics, Dalian University of Technology, Dalian 116023, China)

The electric-heat method is the main cold-proof measure for polar ocean engineering equipment, with thermal balance being key to convective heat transfer.Taking an electric heading plate component as a research object, numerical simulations and model tests were carried out to analyze the influence of complex polar environmental factors on the thermal balance of electric heating of marine engineering equipment.Wind speed and temperature were considered as the main environmental parameters in this analysis; wind speed was varied over the range 0–40 m·s–1and temperature over the range −40–0 °C.Based on FLUENT software simulations and model tests, the convective heat transfer coefficients of the electrical heating plate component under different wind speeds and temperatures were obtained.The results showed that increasing wind speed and decreasing temperature could increase the convective heat transfer coefficient of the plate component.Temperature had little effect on the heat transfer of the plate when the wind speed was stable.In contrast, the convective heat transfer coefficient of the plate increased significantly with increasing wind speed at a given temperature.A mathematical prediction model for the convective heat transfer coefficient of the electrical heating plate component was established based on these experimental data, and the validity of the model was verified by numerical simulation.

polar region, flat plate member, convective heat transfer, experimental testing, numerical simulation

2020年12月收到来稿, 2021年3月收到修改稿

国家自然科学基金(52071055)、辽宁省高等学校创新团队(LT2019004)资助

操太春, 男, 1995年生。硕士研究生, 主要从事海洋工程装备防寒研究。E-mail: caotaichun@foxmail.com

张大勇, E-mail: zhangdy@dlut.edu.cn

10.13679/j.jdyj.20200080