锚杆拉拔过程中径向力学响应特征研究

邓 亮，张 传 庆，汤 艳 春，谭 欢，崔 国 建，周 辉

(1.三峡大学 土木与建筑学院，湖北 宜昌 443002； 2.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071； 3.中国科学院大学，北京 100049； 4.安徽理工大学 土木建筑学院，安徽 淮南 232000)

全长粘结砂浆锚杆支护作为一种有效的支护手段被广泛应用于地下厂房、引水隧洞、基坑及边坡支护等工程，能有效改善被锚固岩体的力学性质及应力分布状态、增强被锚固岩体的整体性，提升岩体强度和变形能力[1]。

大量室内试验和现场锚杆破坏现象表明，全长粘结锚杆的破坏主要发生在杆体-注浆体或注浆体-围岩界面[2]，锚杆拉拔过程中这些界面的力学特性与力学行为对整个锚杆系统的承载力和破坏过程起控制作用，而这些界面的径向力学响应过程又是研究其剪胀位移模式和剪切强度的关键，对揭示锚固系统破坏机制有十分重要的意义。

为研究锚固系统界面力学特性，国内外学者开展了大量室内拉拔试验。Blumel[3]采用中心拉拔试验开展了锚杆拉拔特性研究，得到了不同锚杆表面形态、灌浆材料、加载速率条件下的界面拉拔承载力及其随拉拔位移的变化规律。Kilic[4]通过监测拉拔试验过程中的拉拔力-拉拔位移曲线研究了不同锚杆肋部形态之间锚杆锚固性能。刘波等[5]开展了室内和现场拉拔试验，分析拉拔试验过程中的拉拔力-拉拔位移曲线，并在此基础上提出了杆体-砂浆界面的粘结滑移关系表达式。Aziz等[6]开展了钢套筒拉拔试验，研究了树脂锚杆的拉拔力-拉拔位移曲线与肋间距之间的关系，根据试验结果提出了最优肋间距的概念。吴涛等[7]开展了右旋无纵筋锚杆的钢套筒拉拔试验，研究了不同套筒壁厚和不同肋间距条件下树脂锚杆的拉拔力-拉拔位移曲线，同时通过应变片采集了试验过程中套筒的周向应变，对比分析了两种刚度条件下周向应变之间的差异。赵象卓等[8]开展了4.5 mm和6 mm壁厚钢套筒拉拔试验，研究了左旋无纵筋树脂锚杆在这两种不同刚度条件下的拉拔力-拉拔位移曲线、周向应变变化曲线变化规律。康红普等[9-12]、林健等[13-14]开展了大量套筒拉拔试验，较为系统地研究了影响锚杆锚固性能的因素，得到了不同因素影响下树脂锚杆的拉拔力-拉拔位移曲线变化规律，完善了当前锚杆支护设计理论并提出了成套支护技术。

综上可见，现有研究多侧重于不同杆体参数(锚杆表面粗糙度)下锚杆拉拔力-拉拔位移曲线特性，而在锚杆拉拔过程中，锚固界面径向应力是影响界面抗剪强度的关键因素，对杆体-注浆体和注浆体-围岩界面的剪切破坏起控制作用，对揭示拉拔破坏机制有十分重要的意义。目前，鲜有学者关注拉拔过程中锚固界面的径向力学响应特征，为此，笔者基于厚壁圆筒原理，采用不同泊松比和弹性模量的套筒来模拟工程中常见的围岩边界条件，通过应变片测量套筒的周向应变，然后根据套筒的周向应变计算得到锚固界面的径向应力，进而揭示不同围岩条件下锚固界面的径向应力的演化规律，以期为锚杆破坏机理及工作机制的揭示提供更加深入的认识。

1 等效岩体弹性模量的计算

锚杆在实际工作状态时的边界条件可近似简化为轴对称模型，如图1所示。在此基础上，Hyett等[15]将厚壁圆筒模型引入到锚索的研究中，本文基于厚壁原理推导得到了围岩等效岩体弹性模量的计算公式，其推导过程如下：

图1 等效厚壁圆筒模型Fig.1 Equivalent thick-walled cylinder model

首先，由弹性力学厚壁圆筒问题平面应变的Lame解[16]可知：

(1)

(2)

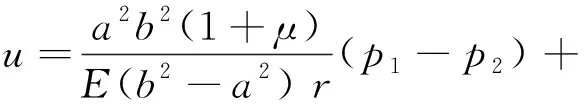
(3)

式中：r为极坐标系下某点的径向位置坐标；p1、p2分别为厚壁内外边界的均布压力；a，b分别为锚杆钻孔和围岩体半径值；E，μ分别为围岩体的弹性模量及泊松比；σr，σθ，u分别为径向应力、周向应力和径向位移。

由于岩体的尺寸远远大于钻孔直径，因此等效厚壁圆筒模型外边界的应力和位移边界条件可认为是p2=0，b→∞。将边界条件代入式(3)可得砂浆基体外壁的径向位移：

(4)

由于刚性套筒的外壁没有约束，即p2=0，将边界条件代入式(1)～(3)，可以得到套筒与砂浆基体界面的应力和位移为

(5)

(6)

(7)

式中：σrm，σθm，um分别为套筒与砂浆界面的径向应力、周向应力和径向位移；Em，μm分别为套筒材料的弹性模量及泊松比；a0，b0分别为刚性套筒的内、外半径。

假设锚杆分别锚固在套筒与岩体中，套筒锚固时砂浆外壁与无限岩体内砂浆外壁的径向位移相等，则可认为锚杆在刚性套筒的锚固效果与围岩的锚固效果近似等效，即存在um=u|r=a，通过联立式(4)、(7)即可得围岩等效岩体弹性模量的计算公式[15]：

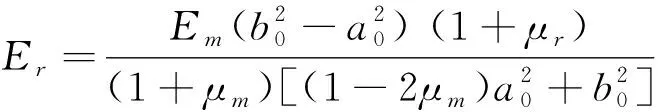
(8)

式中：Er为围岩体弹性模量；μr为围岩体的泊松比，本文统一取为0.3。

2 试验方案及参数

2.1 套筒参数

依据锚杆支护规范[17]，本次试验选取的刚性套筒的内、外径分别为21 mm和27 mm。由公式(8) 可知，在已知刚性套筒的内外径的情况下，可以通过选择不同弹性模量和泊松比材料的套筒来模拟不同刚度的围岩条件，本次试验选取钢、铜、铝、镁合金、PVC等材料来分别模拟硬岩、中硬岩、软岩围岩刚度条件，具体参数如表1所示。

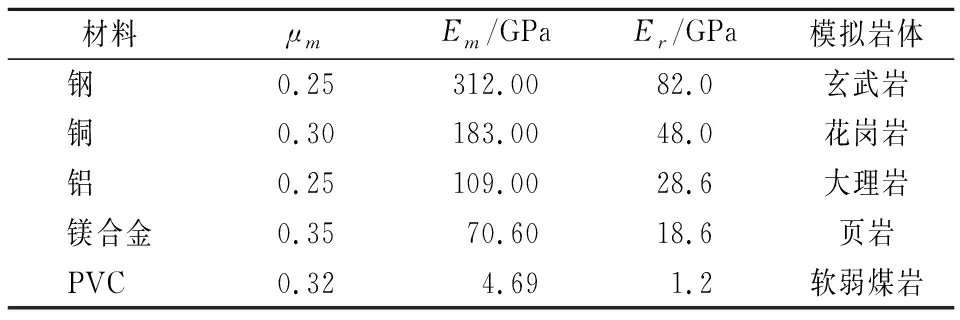
表1 刚性套筒及模拟岩体的具体参数Tab.1 Parameters of rigid cylindrical sleeve and simulated rock mass

2.2 试样制备

根据表1中的材料加工了5种长度为100 mm、内外半径分别为21 mm和27 mm的刚性套筒。本次试验选用的锚杆为矿山巷道支护常用的左旋无纵筋螺纹钢锚杆，其形态参数如表2所示。依据《锚固与注浆技术手册》[18]中建议的配比，本次试验采用标号为32.5的普通硅酸盐水泥、粒径2 mm以下的中粗河砂来配置砂浆(水泥∶砂∶水=1∶1∶0.4)，外加3%水泥质量的甲酸钙早强剂，其3 d单轴抗压强度为26 MPa。

表2 左旋无纵筋锚杆表面形态参数实测值Tab.2 Measured value of profile parameters of left-handed non-longitudinal anchor bolt

为使锚杆中心和套筒中心重合，使用了特制的对中浇筑台(如图2所示)，对中完成以后再向套筒内浇筑砂浆，并手动振捣3～5 min，养护3 d后，将拉拔套筒试样从浇筑台上拆除，养护完成的试样如图3所示。试样养护完成后，将套筒表面的砂浆清理干净，然后在套筒外壁中间位置沿周向均匀的布置4个应变片(间隔90°)，再使用工具将导线焊接在应变片的端子上，完成后的套筒试样如图4所示。

图2 试样浇筑过程Fig.2 Process of sample casting

图3 养护完成的试样Fig.3 Sample after curing

图4 应变片焊接完成后的试样Fig.4 Sample with strain gauge

2.3 试验设备及控制参数

套筒拉拔试验在中国科学院武汉岩土力学研究所锚杆(索)拉拔试验系统RBPT-176上进行，试验机示意图如图5所示。该系统垂直油缸最大出力500 kN，活塞行程为150 mm，可采用力控制或位移控制方式加载，位移加载速率的范围为0.06～50 mm/min，可以实时记录和显示试验过程中的拉拔力和拉拔位移，采样频率为10 Hz。锚杆拉拔试验机采用伺服控制，内置位移传感器，本次试验采用等速位移加载模式，加载速度为0.3 mm/min。应变采集仪采用东华测试DH3816N静态应变测试系统，包含60个测点，系统最高分辨率为1 με，数据采集频率为5 Hz。

图5 锚杆拉拔试验机示意Fig.5 Schematic diagram of pullout test equipment

3 锚杆拉拔力学响应特征

3.1 拉拔力-拉拔位移曲线特性

根据套筒拉拔试验结果绘制了不同围岩等效岩体弹性模量条件下的锚杆拉拔力与拉拔位移关系曲线，如图6所示。从图6中可以看出，拉拔力-位移曲线主要分为以下4个阶段：① 紧密接触段，加载初期在拉拔力作用下锚杆杆体与砂浆紧密接触，并且砂浆内部孔隙也逐渐压密，此阶段拉拔力-位移曲线表现为下凹型，其斜率开始逐步增大；② 线性增长段，随着拉拔力的增大，曲线基本呈现线性关系，当拉拔力达到峰值后开始进入软化段；③ 峰后软化段，当锚杆杆体-砂浆界面达到极限强度后，砂浆与锚杆肋部接触的位置开始发生剪切破坏，界面间的咬合力逐渐下降，抗拉拔性能也随之持续下降，峰值拉拔位移随着套筒刚度的增大有逐渐增大的趋势，PVC筒的峰值位移为2.3 mm，而钢套筒的位移为4.8 mm；④ 残余段，此时的杆体-砂浆界面发生完全剪切破坏，锚杆与砂浆之间拉脱，拉拔位移不断增大，但拉拔荷载基本保持不变，拉拔力主要由破碎后的砂浆与锚杆界面之间的摩擦阻力提供。

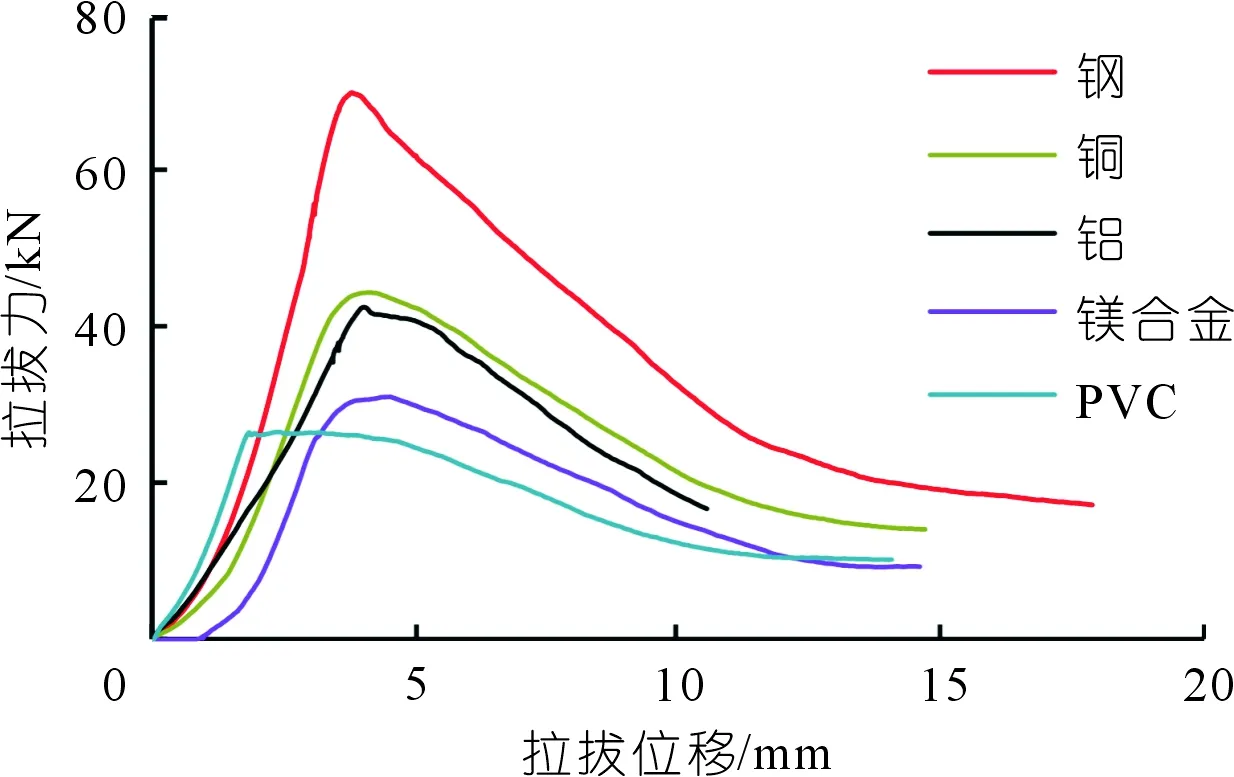
图6 不同围岩条件拉拔力-拉拔位移曲线Fig.6 Pullout force-displacement curve under different surrounding rock condition

3.2 拉拔承载力与围岩刚度关系

锚杆拉拔承载力在锚杆支护设计中是一个十分重要的力学参数，不同围岩刚度下的拉拔承载力如表3所示。为研究锚杆承载力与围岩刚度之间的关系，绘制了围岩等效岩体弹性模量与拉拔承载力的关系图，如图7所示。从图7中可见，围岩等效岩体弹性模量与拉拔承载力成线性关系，同样的砂浆锚杆设置在软岩和硬岩内，其拉拔承载力差异明显。通过拟合，可以得到围岩等效岩体弹性模量与拉拔承载力的经验本构关系：

Fmax=αEr+β

(9)

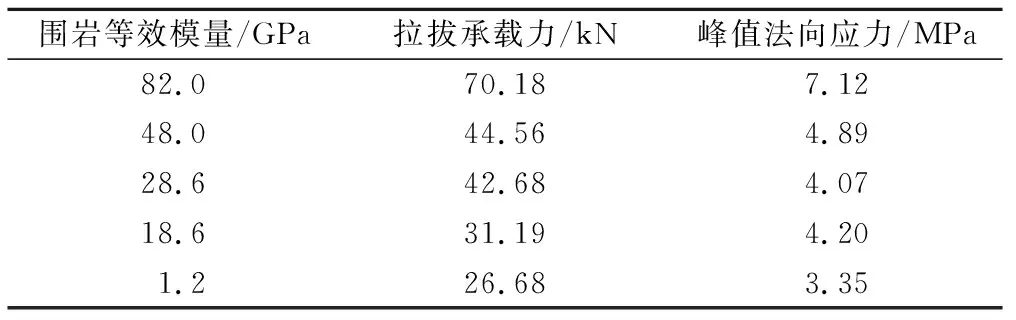
表3 试验过程中锚杆拉拔承载力和峰值径向应力Tab.3 Bolt pullout bearing capacity and peak radial stress of mortar-rock interface during the test

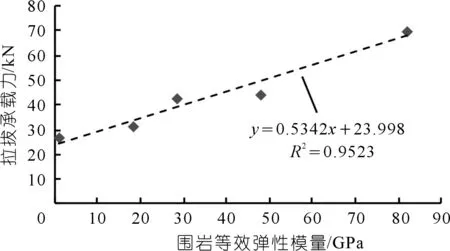
图7 拉拔承载力与围岩等效模量关系Fig.7 Relationship between ultimate pullout bearing capacity and equivalent elasticity modulus of surrounding rock

式中：Fmax为拉拔承载力；Er为等效岩体弹性模量；α、β为与锚杆形态和砂浆强度有关的参数，本次试验条件下α=5×10-4，β=23.998。

4 锚杆径向力学响应特征

4.1 径向应力-拉拔位移曲线特性

假设套筒为各向同性，联立式(5)、(6)，可推导得到砂浆与套筒界面的径向应力，但这一径向应力是拉拔过程中等效界面(为杆体-砂浆界面→砂浆体→砂浆-套筒界面→套筒整个系统力的传递作用结果)的力学响应，界面径向应力计算公式为

(10)

式中：ε为套筒外壁测得的周向应变值。

根据套筒外壁应变片测量得到的周向应变值及式(10)计算得到拉拔过程中砂浆-套筒(砂浆-围岩)界面的径向应力，绘制了界面径向应力-拉拔位移曲线，如图8所示。可见，除了钢质套筒外，其余材质套筒对应的界面径向应力-拉拔位移曲线均在起始阶段表现为径向应力无明显变化，即此阶段径向变形尚未启动，径向应力未产生。随着拉拔变形发展，杆体-砂浆界面开始出现剪切错动，剪胀行为开始显现，径向应力不断升高，并达到峰值后逐渐降低，且相对于峰前升高速率来讲，降低速率较小。原因是围岩等效岩体弹性模量较小时，约束效应较弱，杆体-砂浆界面在到达其峰值剪切强度后砂浆突出部发生剪切破坏并逐渐滑脱，界面的剪胀能力被削弱，径向应力也随之下跌。由于钢质套筒刚度非常大，对径向变形反应敏感，故拉拔变形发生后很快就显现出来，径向应力随之迅速升高，且达到峰值后出现小幅迅速跌落，进而又随着拉拔位移增大而持续升高。原因是围岩等效岩体弹性模量较大时，杆体-砂浆界面主要表现为挤压破碎破坏，因此界面径向应力在越过拐点以后仍然会保持很长一段位移的缓慢增长[19-20]。

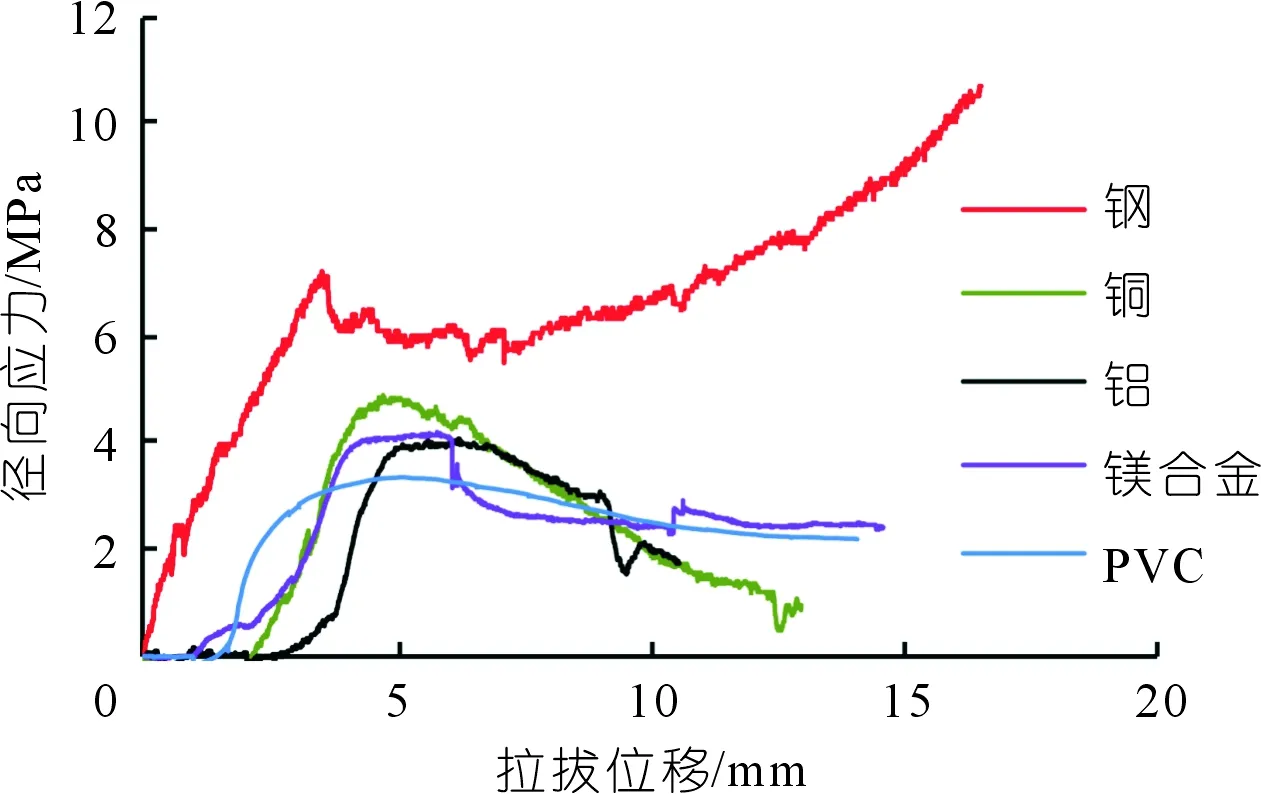
图8 不同围岩条件下径向应力-拉拔位移曲线Fig.8 Radial stress displacement curves under different surrounding rock conditions

4.2 峰值径向应力与围岩刚度关系

为研究界面峰值径向应力与围岩等效岩体弹性模量之间的关系，根据表3中的数据，绘制了围岩等效岩体弹性模量与界面峰值径向应力的关系图，如图9所示。

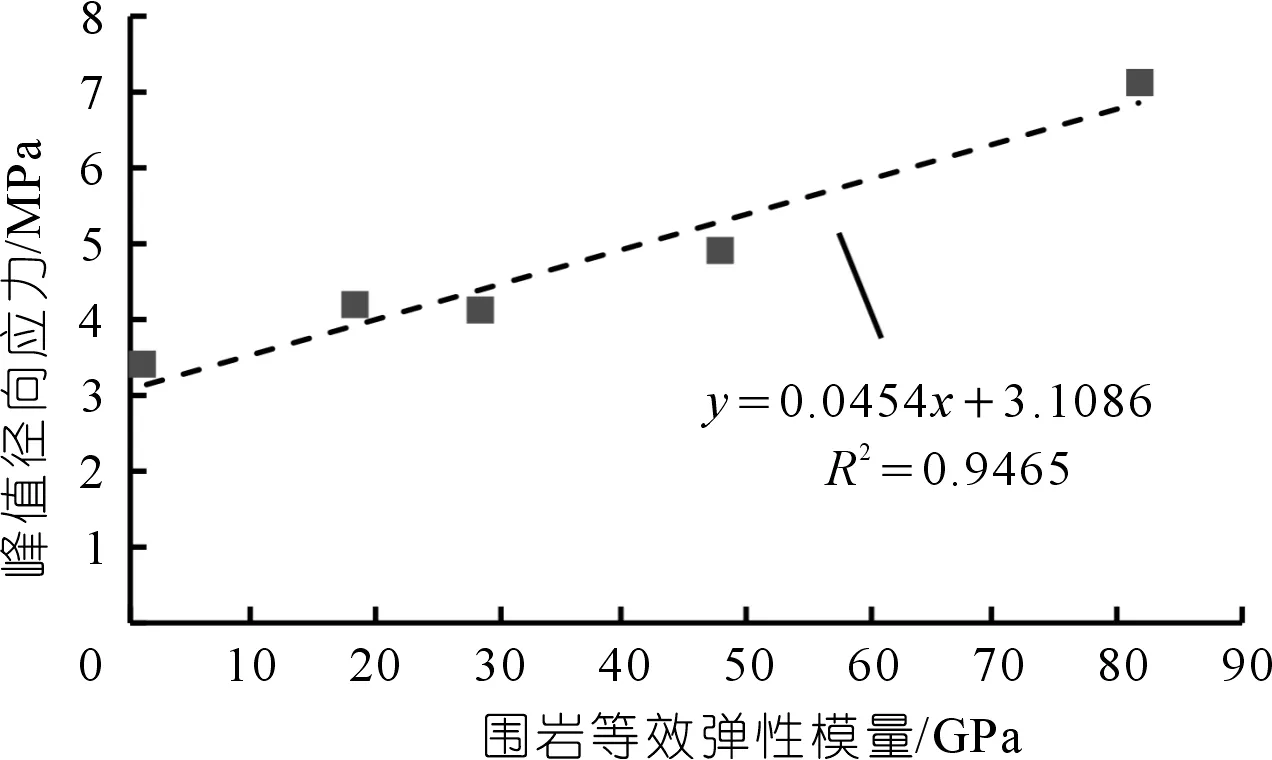
图9 峰值径向应力与围岩等效模量关系Fig.9 Relationship between peak radial stress and equivalent elasticity modulus of surrounding rock

通过拟合，可以得到围岩等效岩体弹性模量与界面峰值径向力的经验本构关系：

σmax=α0Er+β0

(11)

其中：σmax为峰值径向应力；Er为围岩的弹性模量；α0、β0为与锚杆形态和砂浆强度、厚度有关的系数，本次试验条件下，α0=4.54×10-2，β0=3.108 6。

4.3 拉拔力曲线与径向应力曲线对应分析

对比图7和图9，拉拔承载力和峰值径向应力均与围岩等效岩体弹性模量线性相关，因此猜想拉拔承载力与峰值径向应力可能存在某种联系。

为研究界面径向应力与拉拔力的关系，绘制了不同围岩等效岩体弹性模量下径向应力-拉拔位移曲线和拉拔力-拉拔位移曲线的对比图，如图10所示。由图10(a)可见，钢套筒下拉拔力与径向应力曲线差异明显，锚杆拉拔力和径向应力在拉拔位移为4 mm时达到峰值，随着拉拔位移的增大，拉拔力开始逐渐下降，而径向应力在峰后经历短暂下降段后缓慢增长。图10(b)～(e)中铜、铝、镁合金、PVC套筒的径向应力曲线则与拉拔力曲线趋势基本一致，拉拔力和界面径向应力均先随拉拔位移的增大而逐渐增大，峰值径向应力曲线峰值较拉拔力曲线稍有滞后，达到峰值后均逐渐减小，这与Zhang等[21]开展杆体-砂浆界面常法向刚度剪切试验得到的结果基本相符。

图10 不同围岩等效岩体弹性模量径向应力曲线与拉拔力曲线对应分析Fig.10 Correspondence analysis between radial stress curve and pullout force curve under different surrounding rock stiffness

导致上述曲线出现的主要原因是：低刚度条件下杆体-砂浆界面以剪胀滑移破坏为主，在剪胀滑移时，径向变形不断增大，径向应力也升高，而随后砂浆突起局部被剪断后，径向变形不再增大，而是逐渐减小，因此，径向应力也降低；而在高刚度条件下，径向约束强烈，此时砂浆的突出部无法被直接剪断或拉脱，杆体-砂浆界面以挤压破碎破坏为主，突出部发生挤压破碎后，破碎颗粒随着拉拔过程在界面间相互错动，导致了径向变形在出现拐点后又逐渐增大，但由于咬合界面破坏严重，此时的拉拔力仍然减小。

5 结 论

根据厚壁圆筒原理，开展了套筒拉拔试验，研究了砂浆锚杆在不同围岩等效岩体弹性模量下的拉拔力和径向应力演化规律，整理试验结果，得到以下几点结论。

(1) 通过套筒四周均布的应变片测量得到套筒的周向应变，再根据厚壁原理推导得到周向应变与砂浆-套筒界面径向应力转换关系式，为锚杆界面研究提供了新的思路。

(2) 依据曲线特征，不同围岩条件下的径向应力-拉拔位移曲线主要有两种：① 围岩弹性模量较大时，径向应力先随拉拔位移的增大而增大，越过峰值点后先短暂下降然后又缓慢增大；② 围岩弹性模量较小时，径向应力先随拉拔位移的增大而增大，越过峰值点后逐渐减小。

(3) 锚杆拉拔过程中，拉拔承载力和砂浆-围岩界面峰值径向应力与围岩弹性模量均成线性关系。

(4) 围岩弹性模量较小时，径向应力曲线与拉拔力曲线的变化趋势一致，杆体-砂浆界面以剪胀滑移破坏为主。围岩弹性模量较大时，界面的径向力学响应强烈，拉拔力曲线与径向应力曲线的峰后段存在明显差异。

对于砂浆破坏模式的研究，目前的套筒拉拔试验存在局限，拉拔试验在破坏中和破坏后均无法很好地获取破坏过程，针对此问题，笔者将采用界面剪切试验方法开展深入研究。