基于G-LSTM模型的短期径流预报——以长江上游寸滩断面-三峡入库断面为例

方 威，周 建 中，周 超，杨 鑫，王 彧 蓉

(1.华中科技大学 土木与水利工程学院，湖北 武汉 430074； 2.长江勘测规划设计研究有限责任公司，湖北 武汉 430010)

一直以来，学者们都在尝试从物理成因的角度分析和理解流域降雨径流过程，探索其循环规律，即用传统水文模型去模拟降雨径流过程的时空分布、边界条件和物理过程[1]。然而，随着传统水文模型研究的逐渐深入，其考虑的参数越来越多，所需的数据日趋复杂，难以建立一套合理高效的水文模型，导致其计算效率也较低[2]。另一方面，由于流域产汇流过程的复杂性和不确定性等原因，对于参数的率定显得日趋困难，预报模型的精度也不一定随着模型复杂程度的提升而显著提高，甚至会遇到异参同效等问题[3-4]。

针对传统水文模型研究的瓶颈，一些学者尝试使用数据驱动的方式去模拟降雨径流过程。从20世纪90年代开始，人工神经网络(Artificial Neural Networks，ANN)及递归神经网络(Recurrent Neural Networks，RNN)被应用于降雨模拟[5]。然而，Bengio等[6]在研究中发现RNN模型存在网络参数寻优过程的梯度消失问题。为解决这一问题，Hochreiter[2]等对原RNN模型进行改进，提出了长短时记忆神经网络(Long Short-Term Memory，LSTM)。改进后的LSTM网络具有极强的长序列关系拟合能力，被广泛应用于各个领域。在水文预报领域，也有一些学者做出了尝试。Kratzert 等[8]发现LSTM模型不论在单一流域还是在多流域上均有较高的预报能力。Hu等[9]将LSTM与ANN做比较，证明LSTM的预报精度高于ANN。杨强[10]利用LSTM模型对澜沧江乌弄龙水电站进行预见期为1个月径流预测，结果表明LSTM模型的预测精度高。顾逸[11]将LSTM模型与GRU结合，构建Simple-LSTM模型进行中长期预报，结果优于BP神经网络和SVR模型。冯钧等[12]提出一种LSTM与BP组合模型预报场次洪水。殷兆凯等[13]以隐藏层神经元数量为代表，讨论LSTM的复杂程度对模型精度的影响。上述研究多将LSTM应用于流域长期径流预报，而LSTM在短期径流预报方面是否具有同样的性能和表现是一个值得探讨的问题。

众所周知，除了模型结构变化对预报精度产生影响，预报因子的合理选取对提高径流预报精度也至关重要。一般来说，用于模型输入的预报因子与预报时段的实测值之间有着极强的相关性，这样使得利用前时刻的观测值去预报未来值成为一种可靠的方法。然而，上述研究对模型预报因子的选取缺乏深入的探讨。针对此问题，本文引入灰色关联分析法筛选预报因子并分析其有效性。灰色关联分析法是根据灰色因子变量之间的变化趋势来判定联系是否紧密，从中找出关联性强的优势因子。其原理简单，对数据无过多的要求，不会出现定性、定量分析不相符合的情况[14-15]。本文将灰色关联分析法与LSTM相结合，提出了灰色关联分析-LSTM耦合短期径流预报模型(G-LSTM模型)，实现时间序列预测的预见性学习，并探讨模型的模拟精度和应用效果。

1 研究方法

1.1 灰色关联分析

灰色关联分析是以“部分信息已知、部分信息未知”的样本数据为研究对象，通过关联度来判断灰色因子变量之间的变化趋势是否一致，以找出其中的优势和劣势因素，定量分析系统的变化趋势[14-15]，其主要步骤如下。

步骤1。根据评价目的，设X0={x0(1)，x0(2)，…，x0(n)}为系统参考序列，Xi={xi(1)，xi(2)，…，xi(n)}(i=1，2，3，…，m)为比较序列。

步骤2。对参考序列和比较序列均进行均值化处理，即：

(1)

步骤3。计算比较序列Xi对参考序列X0在k时刻的关联系数ηi(k)：

(2)

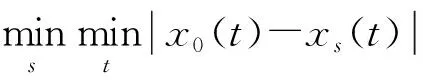
步骤4。计算各个时刻关联系数的均值，作为每个比较子序列和参数序列的关联度，关联度ri计算公式如下：

(3)

步骤5。根据关联度大小，对各个参数序列进行排序，并以关联度大的原则，选出其中关联度较高的比较子序列。

1.2 长短时记忆神经网络

长短时记忆神经网络(Long Short-Term Memory，LSTM)是RNN网络的一种特殊类型，擅长学习长序列依赖信息。与其他神经网络一样，LSTM由输入层、隐藏层及输出层组成(见图1)。

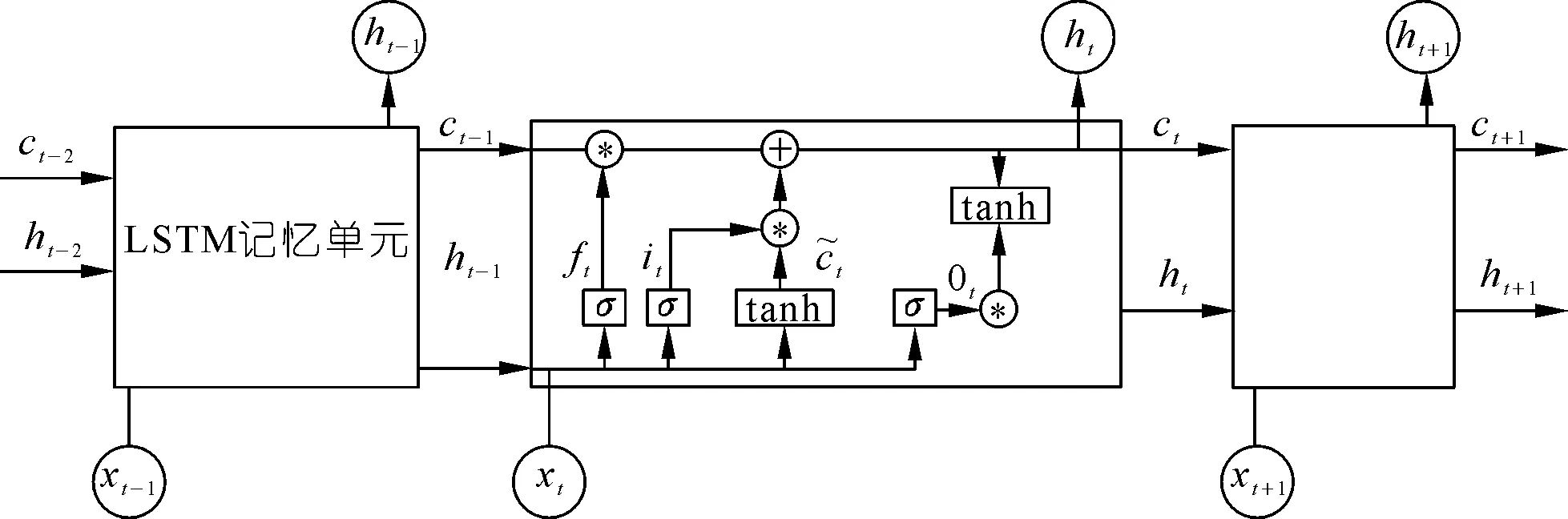
图1 LSTM神经网络结构Fig.1 Structure of LSTM

LSTM算法主要过程如下：

(1)确定模型的预报因子Xt={xt(1)，xt(2)，…，xt(n)}作为模型的输入，并对输入因子进行归一化处理，层层向后传播。

(2)用Sigmoid 激活函数σ处理输入信息xt，前一时刻隐藏层状态变量ht-1，记忆单元状态变量ct-1，得到遗忘门的值ft，即：

ft=σ(Ufxt+Wfht-1+bf)

(4)

(5)

式中：Uf，Wf是遗忘门的可调节权重矩阵；bf是遗忘门的偏置向量。

(3)用Sigmoid激活函数σ得到输入门it，即：

it=σ(Uixt+Wiht-1+bi)

(6)

式中：Ui，Wi是输入门的可调权重矩阵；bi是输入门的偏置向量。

(4)用双曲正切激活tanh函数得到记忆单元的当前时刻的状态变量ct，即：

ct=tanh(Ucxt+Wcht-1+bc)

(7)

(8)

式中：Uc，Wc是记忆单元状态变量的可调权重矩阵；bc是记忆单元状态变量的偏置向量。

(5)用上述计算结果更新神经元状态，即：

(9)

式中：*代表元素的智能乘积，即两矩阵中对应的元素相乘。

(6)用Sigmoid激活函数σ输出门ot的值，即：

ot=σ(Uoxt+Woht-1+bo)

(10)

式中：Uo，Wo是输出门的可调权重矩阵，bo是输出门的偏置向量。

(7)用得到输出门的值和记忆单元的状态变量更新隐藏层状态变量ht，即：

(11)

(8)将更新后的隐藏层的值传入输出层，得到当前时刻的最终输出yt：

yt=Wdht+bd

(12)

式中：Wd是输出层的可调权重矩阵，bd是输出层的偏置向量。

1.3 G-LSTM模型的计算步骤

采用灰色关联分析法与LSTM模型相结合，建立G-LSTM模型，计算步骤如下：

(1) 分析适合径流预报的可能预报因子，利用灰色关联分析法比较预报因子与预报径流的相关程度。

(2) 根据关联度大小，从预报因子集中挑选与预报径流关联程度较大的预报因子。

(3) 以实测径流与相应的预报因子作为输入，驱动LSTM模型，对率定期样本点进行训练。

(4) 根据评价指标，优选LSTM的合适参数。

(5) 采用优选后的LSTM模型对检验期样本点进行预报，检验模型的预报性能。

1.4 评价指标

为了评价所建模型的预报效果，参考SL250-2000《水文情报预报规范》，采用确定性系数、均方根误差、平均洪峰相对误差、平均洪量相对误差指标来评价径流预报结果的优劣。各指标的定义如下：

(1) 确定性系数DC

(13)

(2) 均方根误差RMSE

(14)

(3) 洪峰相对误差PRE

(15)

(4) 洪量相对误差VRE

(16)

2 实例分析

为验证模型的实用性和可靠性，选取长江上游寸滩断面-三峡入库断面作为研究区间，如图2所示，干流长600余km，流域面积约5.4万km2。长江上游流域为亚热带季风气候，夏季暴雨频繁，易发生洪涝灾害，而冬季降雨较少，其年降水量空间分布不均匀，由东南向西北逐渐减少；降雨量年内分配也不均匀，汛期(6～9月)降雨占每年降雨总量的50%～70%。因此，对该区间进行精准、可靠的径流预报对于长江上游流域具有重要意义。

图2 寸滩-三峡入库区间流域概况Fig.2 Overview of study area

收集整理2003～2018年汛期(6～9月)寸滩站、三峡入库、该区间支流重要控制站武隆站的日径流数据，并根据该区间80个雨量站2003～2018年汛期(6～9月)的日降雨数据，利用泰森多边形法将它们转化区间日面雨量。其中，以2003～2014年汛期的降雨径流数据作为模型率定样本，以2015～2018年汛期的降雨径流数据作为模型检验样本。以前期降雨径流数据作为输入变量驱动模型，以三峡入库当前日径流数据为输出变量。三峡入库流量数据是由实测出库流量数据、坝前水位数据以及三峡水库动库容曲线，通过水量平衡方程反算得到；其中动库容曲结是由凤凰山、秭归、巫山等水文水位流量数据近似计算得到。本文数据由中国长江电力股份有限公司提供。

2.1 预报因子辨识

预报因子的选取是模型预报建模的第一步，也是至关重要的一步。根据径流预报的影响因素，选取三峡入库、寸滩站、武隆站前7 d、前1 a同期日均流量以及区间前7 d降雨量共31个预报因子，从中遴选关联度高的预报因子。利用灰色关联分析法计算各预报因子与预报时段实测值的关联程度，如表1所列。

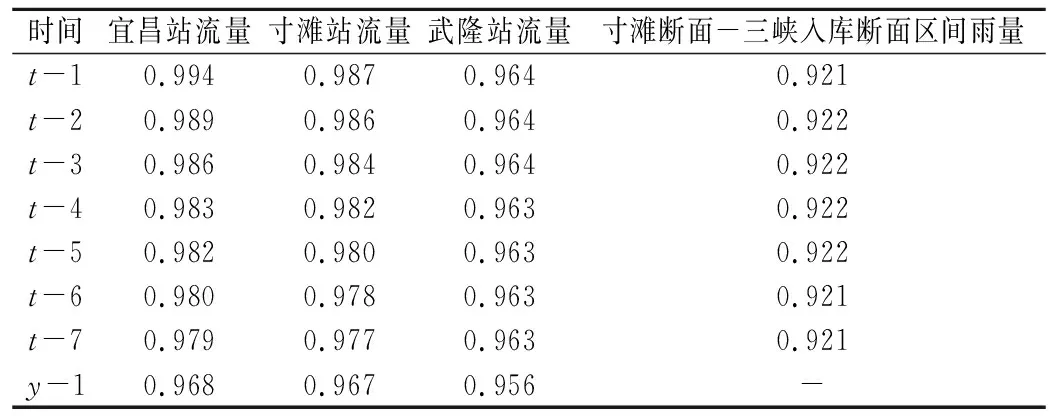
表1 不同时间下各水文站点预报因子的关联度Tab.1 Relevance of each forecast factor of stations at different time

根据关联度大小原则，挑选三峡入库前6 d流量qsx、寸滩站前4 d流量qct作为预报因子，即：

qsx(t)=f[qsx(t-1)，qsx(t-2)，qsx(t-3)，

qsx(t-4)，qsx(t-5)，qsx(t-6)，

qct(t-1)，qct(t-2)，qct(t-3)，qct(t-4)]

(17)

同时作为对比，根据自相关系数法筛选出三峡入库前5 d、寸滩站前3 d、武隆前1 d流量以及前1 d的降雨量作为预报因子。

2.2 各模型径流模拟结果

在G-LSTM的构建过程中，基于上述所选的预报因子，选用寸滩站、三峡入库、2003～2018年汛期(6～9月)的日流量数据构成样本集，选取三峡入库前6个时段的径流量及寸滩站前4个时段的径流量为一个样本。然后确定模型参数和模型结构，综合考虑模型预报效果和复杂度，将隐藏层的个数设置为2层，每层的神经元个数分别为75和100个；在模型参数训练方面，为了对率定期的数据留取一小部分进行自验证，依据经验，将validation_split(率定期训练和验证的分割比例)设定为0.05；一次训练所选取的样本数为1，训练代数设定为100代。模型的率定及检验效果如表2所示。

为论证G-LSTM模型的有效性，分别选用新安江模型、BP神经网络以及LSTM模型进行模拟预测并作对比分析。新安江模型以前期降雨及蒸发数据为输入，考虑区域前期雨强、下垫面因素等初始条件的影响，将模型预热期设置为45 d，并采用多目标文化混合复形差分进化算法MOCSCDE对模型参数进行率定。而传统的BP神经网络按3层结构设计，其输入输出与G-LSTM相同。LSTM模型参数与G-LSTM相同，预报因子选用自相关系数法得到的预报因子。本研究中，将BP神经网络隐藏层的神经元个数设定为13个，学习率为0.5，试算后确定训练迭代次数为4 000次。各模型率定及检验结果如表2所示。

表2 各模型计算结果对比Tab.2 Comparison of different models prediction results

2.3 结果分析

由表2所示：从确定性系数来看，G-LSTM模型率定期及检验期均在0.9以上，精度最优，拟合效果最好；新安江模型率定期及检验期的确定性系数在0.85左右，与G-LSTM的确定性系数分别相差0.09和0.06左右，不如G-LSTM模型的模拟效果好；BP神经网络率定期及检验期的确定性系数均在0.7以上，但其率定期与检验期的模拟效果相差较大，说明其泛化能力较差，与G-LSTM相比分别相差0.07和0.11左右，效果明显不如G-LSTM模型好。而传统的LSTM模型率定期及检验期的确定性系数均在0.9以下。从均方根误差来看，G-LSTM模型均在2 000 m3/s左右，而其他模型的均方根误差均大于2 800 m3/s，表明后者模拟出来的预报值与实测值的偏差更大，拟合的效果偏差。从洪量相对误差来看，G-LSTM模型均小于3.5%，而新安江模型的率定期的洪量相对误差小于4%，率定期却大于8%，结合洪峰相对误差来看，新安江模型检验期的洪峰相对误差高达15.7%，说明新安江模型在全局中对极值点的预报不是十分准确，导致了其在检验期的洪量预测出现较大偏差，拟合效果不佳。而BP神经网络率定期和检验期的洪量相对误差均在9%以上，高于前两者，拟合效果更差。最后，再看洪峰相对误差，G-LSTM均低于9%，且检验期的洪峰相对误差低于率定期的，而BP神经网络的洪峰相对误差虽也均低于9%，但其检验期的洪峰相对误差却比G-LSTM的高出了3%左右，LSTM模型的洪峰相对误差均高于9%，说明G-LSTM模型在全局中对于极值点的拟合能力较好，且泛化能力强，使得检验期的效果更优于率定期，应用效果更佳。所以，综合比较各个模型的拟合结果来看，G-LSTM模型的精度最高，拟合效果最优。

为进一步证明本文建立模型的性能，再分别选取2012年汛期(率定期)和2015年汛期(检验期)数据驱动各模型并对模拟结果进行分析，如图3和图4所示。由图可知：G-LSTM模型的拟合效果明显优于新安江模型、BP神经网络和传统的LSTM模型，尤其是其对每场洪水洪峰的模拟能力更加吻合。而新安江模型和BP神经网络的预报结果均高于实测值。这是因为新安江模型只是模拟自然现象，其参数过多且相互之间相关性过强，使得模型结果不可避免地存在“异参同效”的现象[3-4]，导致对于最优参数的选取存在极大的不确定性。同时，新安江模型的输入相对固定，使得其对数据的准确性存在较大的依赖，这又增加了最优参数选取的难度。BP神经网络虽然结构简单，但其收敛速度慢，效率低下，且泛化能力较差，训练能力和预测能力存在矛盾，使得其精度较差。而LSTM模型在RNN的基础上增加了输入门、输出门、遗忘门3个控制单元，遗忘门会筛选上一时刻输入的径流信息，保留与当前时刻相关性较强的径流信息；然后通过输入门更新当前的输入径流信息，最后通过输出门传送出去，这就使得对某一时段的径流值进行预报的时候，模型不仅考虑了当前时刻输入的预报因子信息，也充分考虑了之前输入的预报因子信息，从而筛选出一组相关性强的输入因子，得出了精准有效的预报流量值，且其收敛速度快而明显，十分适用于长序列数据的拟合。同时，本次研究通过灰色关联分析法预选相关性较高的预报因子，这又增加G-LSTM预报的准确程度。而传统的LSTM模型选取得到的选取预报因子不够准确，不能进行较好地模拟径流，并在预报值和实测值之间出现明显的“时滞”现象，使得预报不佳。因此，利用灰色关联分析筛选出合理准确的预报因子，就是G-LSTM模型优于传统LSTM模型的地方。

图3 各模型2012年汛期模拟结果Fig.3 Simulation results of each model in the 2012 flood season

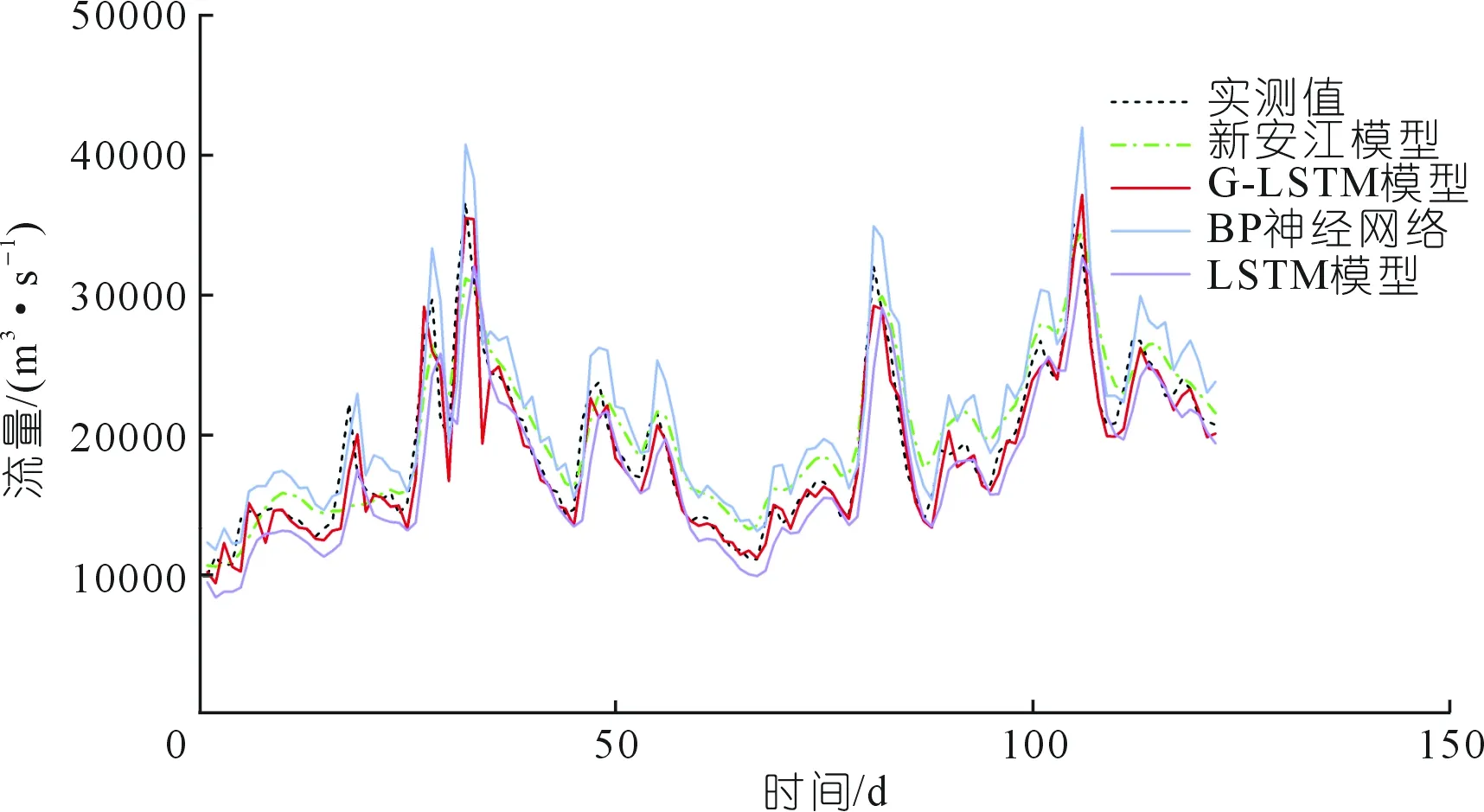
图4 各模型2015年汛期模拟结果Fig.4 Simulation results of each model in flood season of 2015

3 结论与展望

本文将灰色关联分析法与LSTM相结合，建立了多变量高维时序数据与预测变量的低维时序数据映射关系的短期径流预报模型，并用于寸滩断面-三峡入库断面短期径流预报。该方法首先采用灰色关联分析法挑选更具有代表性的预报因子作为模型输入，在一定程度上避免了由于信息不对称带来的损失。然后将G-LSTM模型与新安江模型、BP神经网络和传统LSTM模型进行对比研究，结果表明：基于灰色关联分析法的G-LSTM模型率定期与检验期的确定性系数均在0.9以上，明显优于其他模型，具有极高的预测精度和极强的泛化能力，尤其是在全局性能上对汛期峰值的拟合表现出了极佳的跟踪预报能力。该方法具有一定的工程应用价值，可为短期径流精准有效预报提供新的解决方案。

G-LSTM模型学习率、最大训练代数以及各隐藏层神经元个数等参数的选取仍然依赖于经验。后续研究可引入智能优化算法率定参数，引进信息分解技术挖掘原始样本的可靠信息，并结合动力学随机分布嵌入理论等，以期进一步优化模型，提高模型的精度，使其更加可靠、实用。此外，本研究仅对一个时刻进行预测，后续将对未来更多时刻的预报效果进行研究，以期增强该方法的实用价值。