“同心协力”策略研究

徐嘉怡，聂思宇，王 璐

(天津师范大学 津沽学院，天津 300387)

“同心协力”(又名同心鼓)是一项团队协作能力的拓展项目。要求在保证安全的情况下，尽可能创造更多的颠球记录。该游戏需要队员之间的密切配合，过程中每个人的用力方向、发力时机、力度等因素，均会影响游戏结果。要确定并讨论鼓面倾斜度与每个人发力时间和力度大小的关系，保持鼓面水平，使球自动下落，自动弹起，完成比赛。为使得连续颠球的次数达到最多，主要研究以下两个问题。

问题一：在理想状态下，且每个人都可以精准控制用力方向，制定一个最佳的协作策略，并求出颠球的高度。

问题二：在现实情形下，鼓面会出现倾斜，出现倾斜角度这个量，需要建立模型描述队员的发力时机和力度与某一特定时刻的鼓面倾斜角度的关系。已知队员人数8人，绳长1.7 m,鼓面的初始时刻是水平静止，初始位置较绳子水平下降11 m,设定不同的发力时机和力度，求偏差0.1 s的鼓面不同的倾斜角度。

1 问题分析

问题一的条件是在理想状态下，忽略空气阻力，由于球与鼓之间发生的碰撞为弹性碰撞，所以没有能量的损失，同心鼓是一个质量均匀的鼓体，需要分别分析鼓、球的受力情况，球与鼓的碰撞时刻的受力分析，分别建立满足各种状态下的力学模型。分析球与鼓的运动状态，建立坐标系。可以根据数据信息，利用牛顿第二定律、动能守恒、能量守恒、二阶微分方程，求出该策略的颠球高度，制定团队的最佳协作策略。

问题二相对于问题一复杂一点，因为在现实情况下涵盖事件的不确定性，队员的发力时机和力度都不能得到有效控制。从现实情况出发，在颠球过程中，鼓面由于受力不均会出现倾斜，需要建立较理想的模型，描述队员的发力时机和力度与某一特定时刻的鼓面倾斜角度的关系。根据已知条件：鼓面的初始时刻是水平静止，因为受力不均衡或者发力时机偏差0.1 s时,鼓面倾斜，我们利用动能定理、冲量、受力情况求解。

2 模型假设

A.同心鼓的人数有偶数个人，且不少于8人。B.忽略空气阻力。C.每个人可以精确控制发力方向、力度与时机。D.球与鼓的碰撞为弹性碰撞。E.人围着鼓均匀站立。

3 模型的建立与求解

同心鼓拓展项目问题需要讨论每个人的发力时机及力度，使得游戏在团队协作下能够使连续颠球次数尽可能更多。根据题目所给信息和要求，建立以下数学模型和算法。

问题一：

假设人数为n，在理想状态下，每个人绕着鼓均匀站立，每个人用力均为F，方向取向上为正，队员将鼓从静止的初始位置拉至水平，与球发生碰撞。鼓的重量为M，球的重量为m。

对鼓的运动过程进行分析：以绳水平的高度建立坐标系，可以得到鼓受力为Fx=Fcosθ1(水平方向所受力)Fy=Fsinθ1(竖直方向所受力)，设绳长为l，绳与水平方向的夹角θ1，则鼓的初始位置为(0,0,z0)，z0=-l·sinθ1，由分析得所有队员水平拉力和为0，合力方向竖直向上。根据牛顿第二定律，z(t)满足微分方程

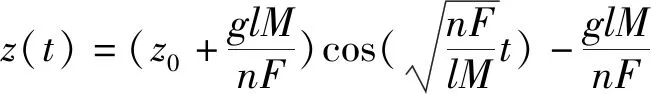
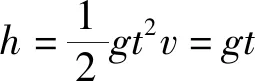
mv1+Mv2=mv1′+Mv2′

解得：

若球从h落下，若想再一次弹到h高度，则v1′=-v1，v=v1，解得：

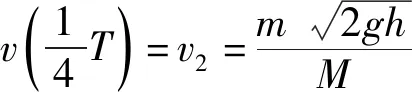
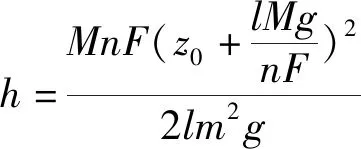
问题二：

同心鼓在受力过程中，由于每个人发力时机及发力大小的不同，会导致同心鼓转动，这时鼓在做刚体转动。

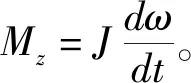
4 模型评价

问题一中为了方便计算，受力分析过程忽略空气阻力，但由于排球的体积较大，空气阻力影响也较大。

问题二中在计算鼓的倾斜角度时，将在鼓面所处同一直径上的两个人对的鼓抽象为一个木棍模型，实际中鼓是一个整体存在，不能将其分割进行单独分析。且在受力分析中假设鼓的中心存在一个轴，进行上下旋转产生倾斜角，实际中鼓的两端由于受力都会同时向上进行运动。