高速路换道意图参数提取及意图阶段确定
任园园,赵兰,郑雪莲,李显生
(吉林大学交通学院,吉林长春 130022)
随着汽车智能化发展,高级辅助驾驶系统(Advanced Driver Assistance System,ADAS)被逐渐应用于车辆驾驶中以提高驾驶安全.ADAS 系统唯有理解驾驶人的意图及动作,才能更好地提供辅助及协作控制策略[1].
近年来,驾驶意图辨识的研究越来越多,机器学习作为主流方法之一,被较多研究学者所使用.在机器学习辨识换道意图的研究中,换道意图表征参数和换道意图阶段确定对模型的辨识效果具有重要影响,过多无用的表征参数会使模型复杂化,降低计算速度,意图阶段截取不当会混入非意图阶段信息,影响意图模型识别效果.因此,意图表征参数组的选择和意图阶段的确定对意图辨识具有重要意义.
意图表征参数可被分为交通环境参数、车辆动态参数和驾驶人行为参数三大类[2].对于具体的意图表征参数选取,现有研究常见提取方法有研究者观察选定、统计学分析差异性、分类器验证三种.Salvucci 等基于驾驶模拟器实验,分析8 位驾驶人的384 次指定换道实验数据,发现驾驶人换道前伴随轻微减速,且意图阶段驾驶人对后视镜的关注明显高于车道保持阶段,因此认为车速及驾驶人视觉特性可以表征驾驶人换道意图[3].李创以NGSIM 数据集作为数据依托,认为横向运动变化规律可以很好地区分车道保持和左右换道三种驾驶行为,选择前车与其初始所在车道左侧车道线的距离、前车的横向速度以及纵向速度作为观测变量[4].以上为研究者通过观察参数在不同驾驶阶段的差异性后确定意图表征参数.除此之外,侯海晶基于驾驶人视觉特性,采用独立样本T 检验,分析驾驶人在左、右换道和车道保持阶段的视觉特性差异,确定驾驶人意图表征参数组[5].毕胜强等人对人-车-路参数构造不同组合,通过分类器验证各组合的分类性能,确定包含人-车-路三者信息的参数组合最优[6].以上学者采用不同方式选取了人车路不同方面的参数用于意图辨识.为降低模型计算复杂度,提升模型精度,本文从参数重要度及相关性角度,选取在意图辨识中重要度高且互相关性低的参数.
在换道意图辨识研究中,意图阶段数据是驾驶人意图的重要表征.常用意图阶段确定方式有两种:一种是通过确定意图起、终点得到意图阶段数据,另一种是确定换道开始点并反向截取一个固定长度得到意图阶段数据.在意图起终点确定意图阶段的方式中,意图起终点多是由观察者观察视频或分析参数变化确定.Kiefer 等人提出将驾驶人开启一侧转向灯或第一次注视后视镜作为换道意图的起点,将驾驶人为完成换道首次转动方向盘为换道意图的终点,二者差值即为换道意图阶段[7].长安大学袁伟、马勇、彭金栓等人基于实车实验数据,以驾驶人首次关注后视镜与横向位置显著变化时刻的时间差为换道意图阶段,经统计得到驾驶人换道意图阶段长度为5 s[8-10].冯杰以驾驶人首次关注后视镜与方向盘转角发生变化的时间差为意图阶段,同时,得出冲动型、普通型和谨慎型驾驶人的意图阶段分别为2 s、3 s、5 s[11].侯海晶、Kuge 等人均提取从直行到方向盘转角出现第一个峰值之前的数据作为意图阶段[12-13].对于第二种换道开始点结合固定长度截取意图阶段数据的方法,换道开始点多由单指标或多指标确定,而意图阶段长度多由参数分析、对比试验获得,宽度不一.其中美国NTHSA 报告根据8 667 次车道变换样本的深入分析发现,换道前3 s 左右足够捕捉驾驶人的视觉搜索规律,确定3 s 为换道意图阶段长度[14];霍克观看218 次试验换道录像发现驾驶员产生意图到实施动作一般要6 s,故确定换道决策阶段为车道变换前6 s[15].Doshi 等人根据视觉特性,分别选取意图阶段为2 s 和3 s 进行识别比较,发现提前2 s 的识别成功率高于3 s[16].Fitch 等人将驾驶员注视划分区域,通过对比意图阶段长度为8 s 和3 s 内驾驶员的视觉区域注视规律,得3 s 左右可见视觉区域有明显差异且设为意图阶段[17].综上,现有的意图阶段确定方式大多建立在视频观察、数据统计分析和试验对比的基础上,易受研究者主观因素的影响,且均用一个固定长度来描述意图阶段.在换道意图研究中,意图阶段易受驾驶人因素影响,换道样本间的意图阶段的位置与长度存在差异,并不完全相同,在此基础上,本文提出一个基于聚类的意图阶段提取方法,在减少研究者主观因素的同时,对每个换道样本单独提取意图阶段数据.
本研究从驾驶模拟器换道数据入手,提出一种换道意图表征参数选择和意图阶段确定方法,并建立高斯隐马尔可夫模型进行高速路换道意图辨识.论文研究成果可以为意图识别研究中意图表征参数的选取及意图阶段的确定提供参考,更准确高效地辨识换道意图.
1 试验设计及数据处理
1.1 试验平台
试验使用交通运输部公路科学研究所(RIOS)研发的RADS 型8 自由度全景驾驶模拟系统(图1)采集驾驶模拟器数据.该驾驶模拟系统主要由6DOF、Yaw-Table、Vibration、X-Table、客舱、多通道投影系统、声响系统、电源系统及其他辅助系统构成,可通过UC-win/Road 软件快速进行三维道路建模和交通模拟,并采用Carsim 车辆动力学软件对车辆动力学参数进行模拟.此外,系统可外接Facelab/Tobii 等眼动系统以及多导心生理采集系统,以实现人车路环境多维参数的采集.

图1 RADS 型8 自由度全景驾驶模拟系统Fig.1 RADS 8 DOF panoramic driving simulation system
1.2 试验场景与实验人员
试验场景涵盖城市路段和高架快速路段两种类型,全程10.35 km,共包含11 个弯道路段,最小转弯半径为100 m,最大转弯半径为300 m.道路形式包含两种,分别为双向双车道和双向四车道,高架快速路车道宽度均为3.25 m[18].该研究主要为高速路段驾驶人换道意图辨识,故只选择试验路线中间部分高架路段数据.场景如图2 所示,主要包括路边建筑物、路边树木及其他机动车辆,其他机动车辆的运动状态为自由设定.被试驾驶员在实验中,均按照个人的驾驶习惯按预先设定的路线进行自由驾驶,自主换道.
试验共选取了17 名被试驾驶人,其中女性驾驶人6 名,男性驾驶人11 名.所选驾驶人均身体健康,无视觉、听觉、心脑血管等疾病.被试基本信息表如表1 所示.试验开始前让所有被试驾驶人充分熟悉驾驶仿真平台,每个驾驶人要求以80 km/h 到120 km/h 的车速完成整个试验.

表1 参与实验驾驶人基本信息Tab.1 Basic information of the experimental driver
1.3 数据采集与预处理
该驾驶模拟系统可同时采集车辆运行状态参数、交通流环境参数、驾驶人眼动行为以及心生理状态,可同时输出123 个不同的动态参数,采样频率为60 Hz,与研究相关的参数有22 个,如表2 所示.其中与车辆运行状态相关参数有16 个,与车辆位置相关参数有6 个.在驾驶模拟实验过程中,由于驾驶人操作失误或设备本身等原因,导致异常或丢失数据的产生,最终采用其中14 个驾驶人试验数据进行研究,利用滑动平均值算法对数据进行滤波处理.

表2 初始参数Tab.2 Initial parameters
本研究定位于换道意图的辨识,在不知具体换道意图阶段的位置时,本文截取从车辆尚处于直行状态到车辆越过车道线的时间段为最初研究样本,可以确定此方式截取的样本必定包含换道意图阶段,具体截取示例如图3 所示.车辆横向位置轨迹与车道线的交点对应时间为车辆跨过车道线的时刻Tlc,以此往前推,找到车辆直行状态末期Tlk,截取Tlk与Tlc之间的数据段用于下文换道意图参数及换道意图阶段确定.
采用MATLAB 中findpeaks 函数寻找到峰值点,该点为局部最大值,为保证所选换道片段不缺失有效数据,从峰值点处往前2 s 作为车辆直行阶段末期Tlk.以此方式最终获取180 组有效样本,包括换道样本112 组(左换道62 组、右换道50 组)和车道保持68 组.所有有效样本将被分为两部分:训练样本和验证样本,比例约为2 ∶1.
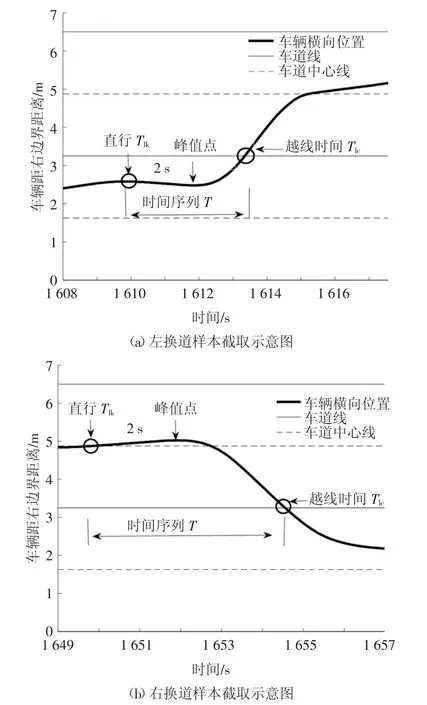
图3 样本截取示例Fig.3 Sample extraction example
2 换道意图表征参数的选取
换道意图辨识研究中,表征意图的参数众多,为减少模型计算复杂度,需要筛选出对区分换道意图重要度较高的换道意图表征参数.本文基于决策树原理进行重要参数的选择.选择决策树算法时,考虑到参数的统计特征取值较多及统计特征之间取值数目不同,选择了可以分裂为多叉树的C4.5 算法进行参数统计特征重要度分析.在进行换道意图表征参数选取时,首先基于C4.5 算法计算参数统计特征的信息增益率GR(Gain Ratio),初步筛选出一组参数,然后进行皮尔逊相关性分析,逐步剔除掉互相关性高的参数,最终得到在意图分类方面重要度高且互相关性低的意图表征参数组.
2.1 参数统计值构造
在上节提取的22 个参数、180 组有效样本中,从每个参数的时间序列中构造对应参数的9 个统计特征,分别为平均值、众数、最大值、最小值、25%分位数、中位数、75%分位数、标准差、方差,22 个参数共计198 个统计特征.鉴于此处参数的时间序列较短,均值、最值、中位数、方差、百分位数等统计值可以大致反映时间序列的变化趋势,故本文采用时间序列的统计特征来表示时间序列,通过分析参数时间序列对应的统计特征的重要度,反映参数的重要度.
2.2 基于C4.5 算法的参数重要度分析
C4.5 算法采用信息增益率作为特征选择指标,信息增益率越大,分裂后的集合有序程度越高,特征的分类效果越好.C4.5 算法进行特征重要度分析流程如图4 所示,图中特征A 代表198 个统计特征中的任意一个.
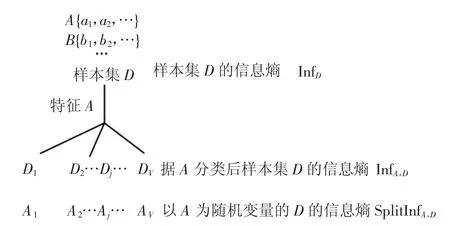
图4 C4.5 算法特征分析Fig.4 Feature analysis of C4.5 algorithm
首先,每个换道样本有198 个特征,将180 组包含左换道、右换道和直行三类样本的特征集作为样本集D,用信息熵InfD来描述样本集合D 的不确定度.

然后以特征A 为依据将样本集D 分为v 类,此时样本集的信息熵为InfA,D.

利用特征A 对样本集合D 进行划分所得到的信息增益为GA,信息增益越大,集合D 的不确定度下降越多.

但是,使用信息增益评价一个特征的分类性能存在缺点:信息增益偏向于选择取值较多的特征,容易过拟合.因此,在信息增益的基础上,除以分裂信息SplitInfA,D[19],得到信息增益率GRA.

把22 个参数所构造的198 个统计特征的信息增益率按由高到低排序如表3 所示.

表3 参数统计特征的信息增益率排序Tab.3 Order of gain ratio in parameter statistical characteristics
为获取重要度较高的参数,将每个参数的9 个统计特征的信息增益率排名表示为一个箱线图.图5为198 个参数统计特征的信息增益率排名对应的箱线图,横轴为表2 中参与重要度排序的22 个参数,纵轴为参数统计特征信息增益率排名.箱线图中每个箱子都可以代表对应参数的9 个统计特征的信息增益率排名情况,中间线表示信息增益率排名100的位置,线以下的10 个箱子,即为信息增益率排名前10 的参数,分别是方向盘转角、侧向加速度、横摆角速度、侧倾角速度、横摆角加速度、车道偏离量、侧倾角、车辆距离左、右边界的距离和道路偏离量.
将以上参数的统计特征作为决策树的分裂节点,进行原始数据的分裂,分裂后的数据集,信息增益率大,混乱程度降低明显,反映出此10 个参数在区分不同驾驶阶段意图时有较好的分类效果,符合意图表征参数要求,为确保各参数之间的独立性,还需要进一步分析参数之间的相关性.

图5 参数统计特征信息增益率排名复式箱线图Fig.5 Gain ratio in parameter statistical characteristics ranking’s double box line chart
2.3 表征参数相关性分析
在上述参数中,车辆离左、右边界的距离与道路偏离量易受道路线形的影响,而本文主要研究高速路上直行后的换道,故排除以上三个参数,只对剩余7 个参数做皮尔逊相关性分析,所得结果如表4所示.

表4 参数的皮尔逊相关性分析Tab.4 Pearson correlation analysis of parameters
在显著性水平P 值均小于0.05 的条件下,排除掉相关系数值大于0.5,即互相关性较高的参数,剩余参数为互相关性较低的参数,分别为方向盘转角、横摆角加速度和车道偏离量.因此综合参数重要度与皮尔逊相关性分析,最终将方向盘转角、横摆角加速度和车道偏离量作为驾驶人换道意图的表征参数,为下文意图识别模型的训练提供观测层输入参数.
3 换道意图阶段的确定
换道意图是驾驶人与周围环境交互后产生的结果.具体地说,当驾驶人对当前车道的满意程度下降,且对目标车道期望程度上升,则会形成换道意图.而具体的换道意图阶段是指,驾驶人产生换道意图时间点至驾驶人执行换道机动时的时间点,这二者之间的时间间隔.作为整个换道进程中的一部分,换道意图阶段具有位置、长度两个属性,且不同换道过程的换道意图阶段也不完全相同.
本文结合车辆到达分道线前参数的阶段性变化,提出一种基于K-means 聚类的换道意图阶段的截取方法,提取训练样本的换道意图阶段训练换道意图识别模型.
3.1 观测集与聚类个数的确定
车辆换道意图表征参数中的方向盘转角和车道偏离量分别代表了驾驶人的动作与车辆的横向位置,最能直观体现车辆换道过程中的动态变化.因此,观测集为方向盘转角和车道偏离量的时间序列.
车辆从直行到跨越车道线,驾驶人通过操纵方向盘实现车辆偏离,又因方向盘具有自由行程,导致方向盘转角变化较早,存在换道意图形成(预转向)到换道意图实施(正式转向)两种状态的过渡,可通过聚类算法中的最小距离准则得到换道意图形成的位置.而车道偏离量反映了车辆的横向位置,其变化晚于其他参数,可以体现换道意图(预偏离)到换道执行阶段(正式偏离)的过渡,可通过聚类算法中的最小距离准则得到换道执行阶段即意图阶段结束的位置.故将方向盘转角和车道偏离量观测集的聚类个数均定为2.
考虑到驾驶人的驾驶风格会导致参数阈值多样化,而此处重点在于换道意图阶段的确定,故在不改变参数变化趋势的条件下,先对时间序列中参数值归一化后再作为K-means 聚类分析的观测集.
3.2 基于K-means 的换道意图阶段确定
换道意图阶段确定方法的流程图如图6 所示,基于文中1.3 节所截取的换道样本,采用车辆从直行到越过车道线的方向盘转角序列和车道偏离量序列作为观测集.
以左换道为例,换道过程中,方向盘转角值的变化要克服方向盘的自由行程及直行阶段方向盘的正常变化范围,此过程为换道与直行共同存在的阶段,即意图形成过程,也称预转向过程,此后的方向盘转角变化可区分直行与换道,为正式转向过程,故将方向盘转角从预转向过程到正式转向过程的分界点定为换道意图开始时刻.

图6 换道意图阶段确定方法Fig.6 Method for determining the intention stage of lane change
而车道偏离量作为驾驶人操纵行为的最终表现,其变化较晚,故基于车道偏离量的聚类结果所得的意图阶段结束时刻可最大程度涵盖意图阶段信息.从安全角度,驾驶人确定换道意图后会存在换道可行性判断过程,即换道意图实施中的对换道安全的考量过程,此时车道偏离量为预偏离过程,在确认换道安全后,即开始真正的换道执行动作,到达正式偏离过程.故将车道偏离量从预偏离过程到正式偏离过程的分界点定为换道意图结束时刻.
单个换道样本聚类结果如图7 所示,上方为方向盘转角聚类结果,下方为车道偏离量聚类结果.


图7 单个样本聚类结果Fig.7 Single sample clustering results
按照图7 的方式,对112 个换道样本进行Kmeans 聚类,不同换道样本的方向盘转角和横向偏离量聚类后的分界点对应的时间不完全相同,符合实际换道情况.
3.3 K-means 聚类结果验证
Sil 指标,又称轮廓系数(Silhouette Coefficient),可评价类的密集程度与分散程度[20].Sil 指标的变化范围是[-1,1],其值越大说明聚类效果越好.表5 为聚类后所有样本点的平均Sil 值,左右换道样本的方向盘转角和车道偏离量聚类后的样本点轮廓系数为0.8 左右,可知本节K-means 聚类结果是合理的.

表5 聚类后样本点的轮廓系数Tab.5 Silhouette coefficient of sample points after clustering
3.4 换道意图阶段的分析
将14 个驾驶人的112 段换道训练样本数据,按照上述换道意图阶段的确定方法,计算每个换道样本的意图阶段并统计所有换道样本的意图阶段长度和每位驾驶人左、右换道平均意图阶段长度,所得结果如图8 和表6 所示.


图8 换道意图阶段长度统计Fig.8 Statistics of lane change intention stage length
对全部被试者的换道意图阶段进行统计分析,其意图阶段长度的均值和标准差如表6 所示.
据统计结果,发现如下规律:
1)由图8(a)(b)整体来看,左换道意图阶段长度大于右换道意图阶段长度,图8(c)为每个驾驶人的左、右换道意图阶段长度平均值对比,黑色柱为左换道意图比右换道意图阶段多余时间段占右换道的百分比.结合图3 分析原因:左边车道为快速车道,右边车道为慢速车道,左换道为向快速车道变换,驾驶人的观察时间会较长,且提前偏离中心线朝着目标车道行驶;右换道为从快速车道向慢速车道变换,驾驶人观察判断时间短,不需要提前偏离中心线行驶.
2)图9(a)(b)为每个换道样本的平均车速与Kmeans 所得每个样本的意图阶段长度的关系图,图9(c)为单个驾驶人的换道意图阶段长度与平均车速的关系图,此处仅列举了四名驾驶人.据图可知,当车辆的平均车速增加时,意图阶段长度近似线性下降.车速较低时,意图阶段长度的分布较为分散、数值偏高且跨度大;当车速升高时,意图阶段长度的分布较为集中且数值偏低.即高速车辆的换道意图阶段相较于低速车辆换道意图阶段更短.这说明高速行驶的车,驾驶人换道前考虑迅速,意图阶段短,车辆能在短时间内完成直行到换道阶段的转换.

图9 意图阶段长度与平均车速关系图Fig.9 Relationship of the intention stage length and average velocity
4 基于CHMM 的换道意图辨识
4.1 模型设计
驾驶人的换道行为具有强时序性,且当前的状态仅依赖于上一个状态,因此选择左-右链隐马尔可夫结构.利用方向盘转角、横摆角加速度和车道偏离量组成的意图表征参数组在意图时间窗内的数据,训练左换道意图(LCL)、右换道意图(LCR)和车道保持辨识模型(LK).
一个完整的CHMM(Continuous Hidden Markov Model)模型可用一个7 元组λc={N,M,β,A,Cjm,μjm,∑jm}表示.
其中β和A 在满足左-右链条件下随机取值,高斯概率密度函数的参数Cjm,μjm,∑jm由K-means聚类赋初值,N 和M 定义如下:
1)N 表示CHMM 模型中的隐状态数目.在左右换道意图辨识模型中,换道意图阶段均分成换道意图的形成和换道意图的实施两个阶段,即状态数N为2.
2)M 表示高斯概率密度函数的个数.模型输入参数的时间序列可由M 个高斯概率密度函数拟合得到,对意图表征参数组的时间序列样本进行高斯密度函数拟合分析,可得三个模型的M 分别为2、3、2.
4.2 模型训练
将三种识别模型基于各自的训练库数据分别训练可得最优参数组λc={N,M,β,A,Cjm,μjm,∑jm}.
训练样本集为方向盘转角(δs)、车道偏离量(Δxlane)和横摆角加速度(ayaw)的时间序列:

各意图模型训练、验证及测试样本如表7 所示.

表7 各意图模型所用样本数据Tab.7 Sample data used for each intent model
基于HMM 工具箱编写脚本程序,采用3 折交叉取样法训练模型,得到训练后的模型部分参数见表8.

表8 优化后的模型参数Tab.8 Optimized model parameters
4.3 识别准确性评估
所有验证样本数据进行意图识别的识别准确率如表9 所示.

表9 验证样本识别准确率Tab.9 Recognition accuracy of test samples
4.4 识别时效性评估
在行驶过程中,驾驶人的意图是一个连续变化的过程.除了预测准确率之外,预测的实时性也是影响预测模型实际应用价值的重要因素.采用滑窗法对连续的驾驶过程进行实时意图识别验证.
利用表7 中时序性测试样本进行换道意图识别模型的时效性评估,其中左、右换道样本各11 个,均取自车辆从直行至越过分道线.基于测试样本的换道意图辨识过程如图10 所示.图10(a)(b)换道过程示意图中的换道开始点为K-means 聚类得到的意图阶段结束时刻.图10(c)(d)为测试样本的换道意图辨识结果.


图10 换道意图辨识示意图Fig.10 Recognition of lane change intention
11 个测试样本识别结果如图11(a)和(b)所示.倒三角为换道开始时刻,正三角为对应意图被正确识别的时刻,两点间线的长度为相对于换道开始时刻的意图识别提前量,左换道意图识别提前量均值为1.5 s,右换道意图识别提前量均值为1.4 s.

图11 时序性测试样本意图识别结果Fig.11 Verification of timing samples intention recognition results
5 结论
针对意图识别研究中意图参数的选择问题,基于决策树C4.5 算法和皮尔逊相关系数,对换道过程中的22 个参数进行了重要度和相关性分析,最终筛选出方向盘转角、车道偏离量和横摆角加速度作为换道意图表征参数组.针对驾驶人换道意图阶段的确定问题,基于K-means 对方向盘转角和车道偏离量的时间序列聚类,得到14 个驾驶人的所有换道样本的意图阶段长度,简要分析得出意图阶段长度与平均车速近似线性相关,且左换道意图阶段长度大于右换道意图阶段长度.采用所得意图表征参数组及意图阶段,基于高斯隐马尔可夫理论建立驾驶人向左、向右换道意图识别模型和车道保持模型,结果显示:意图识别模型的平均识别准确率为90%;直行路段上,该模型可以在左换道开始前1.5 s、右换道开始前1.4 s 预测出换道意图.

