含边界层的机械臂分数阶滑模控制
刘世杰,黄志来,杨明星,徐培民
(安徽工业大学 a.特种重载机器人安徽省重点实验室;b.机械工程学院,马鞍山 243000)
分数阶微积分是整数阶微积分的拓展,由L’Hopital 和Leibniz 于1695 年首次提出[1],进一步演变为微分/积分阶次为任意复数,称之为复数阶微积分[2].分数阶微积分在控制领域的应用受到许多学者的关注[3],并将其移植于整数阶控制器,取得了系列研究成果[4].
滑模控制(Sliding Mode Control,SMC)[5]是一种确定、非线性、鲁棒控制方法,属于变结构控制[6],滑模面对应的函数满足李雅普诺夫稳定[7],保证系统相轨迹在预定的滑模面附近切换,实现稳定控制[8].引入分数阶微积分设计滑模控制是当前研究的热点[9],对解决滑模控制所固有的抖振问题有积极意义[10],并具有更好的控制效果[11].分数阶微积分应用于滑模控制,简称分数阶滑模控制 (Fractional Order Sliding Mode Control,FOSMC),在控制器的设计过程中,部分学者将分数阶算子与滑模面结合构成分数阶滑模面.Huang 等[12]针对多机电力系统,将分数阶微积分应用于滑模控制,提出一种自由空间滑模控制器,仿真结果表明该控制器能有效减少抖振现象.Nguyen 等[13]针对半主动车辆悬架系统,提出一种基于分数阶导数的滑模控制器,数值仿真验证所提出的控制方法能使给定系统的状态在有限时间内渐趋稳定.此外,还有学者将分数阶算子与趋近律结合构成新的分数阶趋近律.Ma 等[14]针对不确定离散时间系统,将分数阶微分和高阶扰动补偿器引入趋近律中,提出一种新的分数阶趋近律,仿真结果表明所提出的方法能进一步减轻抖振并提高控制精度.Babaei 等[15]将非线性趋近律与基于分数阶模型的灰色预测算法相结合,提出一种新的分数阶模糊灰色预测滑模控制器,仿真和试验结果显示,所提出的方法跟踪速度更快,对干扰具有较强的鲁棒性.
机械臂广泛应用于装备制造、外科医疗等领域[16],随着工业领域对效率和质量的不断追求,对机械臂系统控制也有了更高要求[17],如控制系统的稳定性[18]、精确的轨迹跟踪[19]等.将分数阶滑模控制器应用于机械臂控制有很好的前景[20].
本研究引入分数阶微积分,构造一类分数阶滑模面和饱和函数趋近律,获得新的分数阶滑模控制器,并证明控制系统的稳定性,最终通过机械臂系统的控制算例验证其控制效果.
1 分数阶微积分
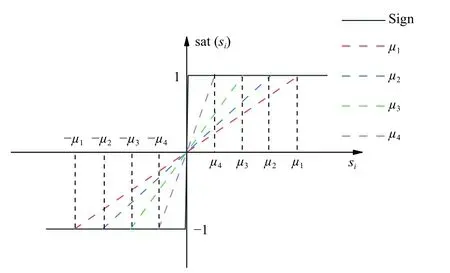
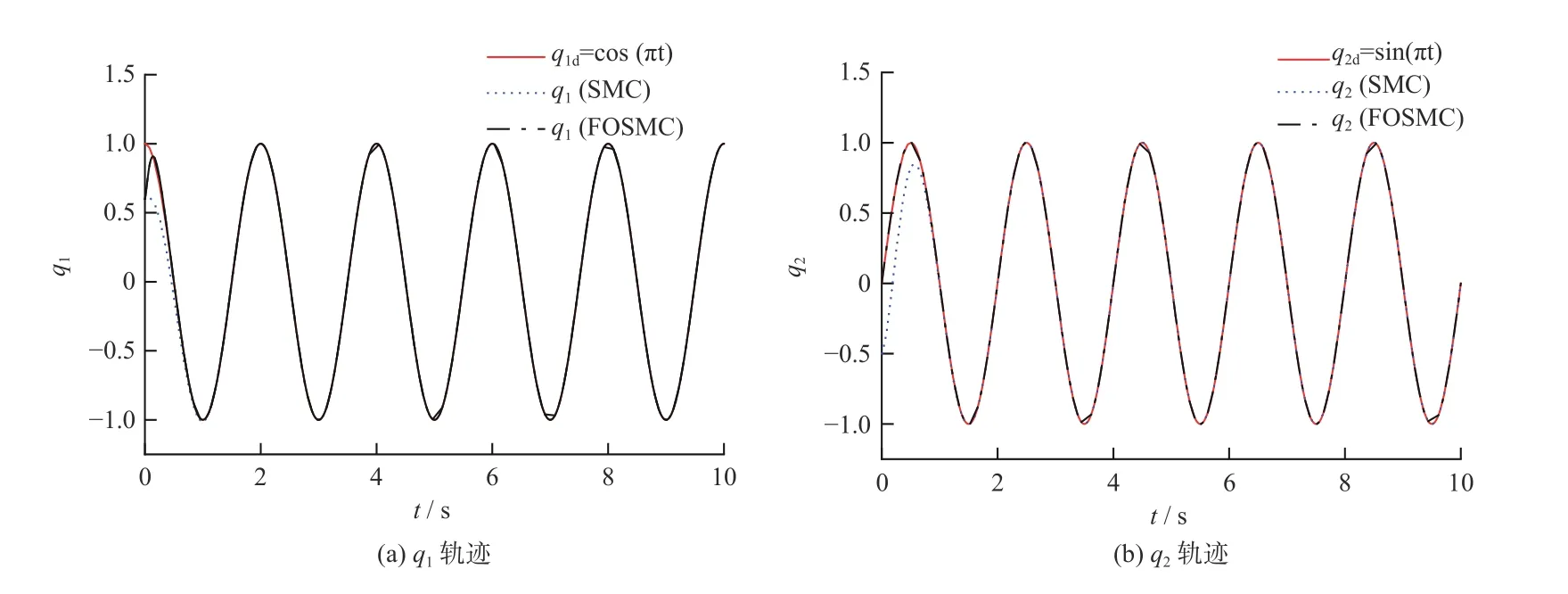
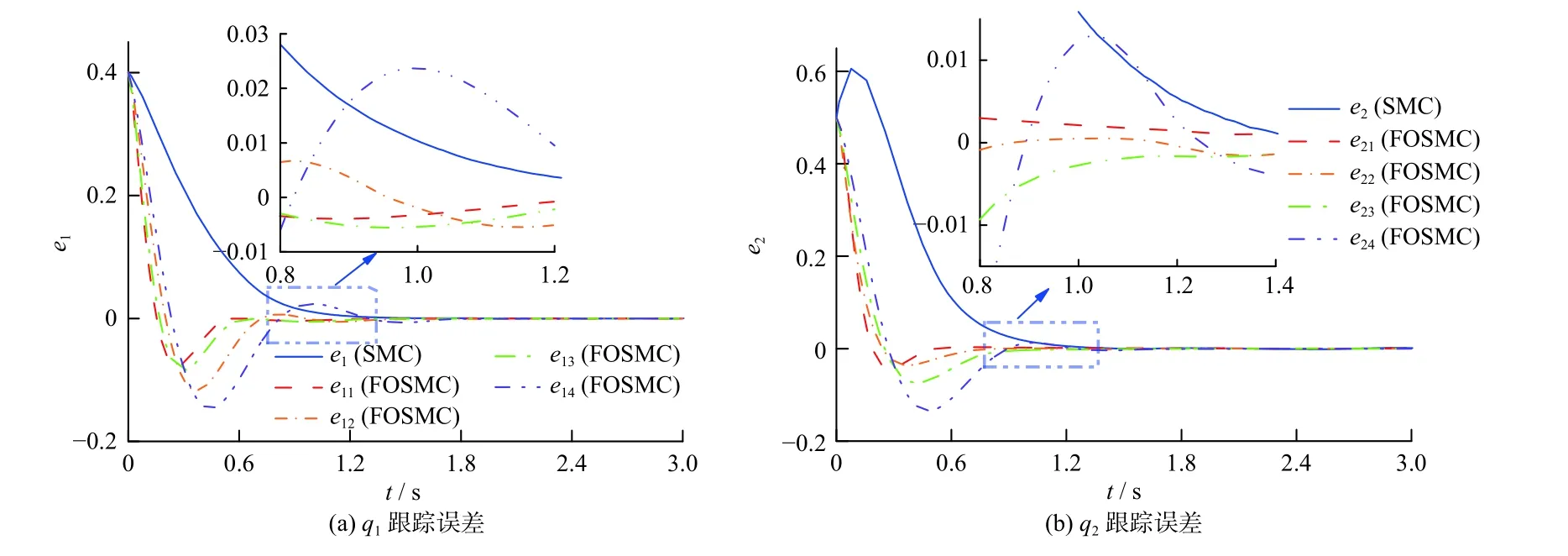
分数阶微积分由整数阶微积分推广至任意非整数阶,近年来,其大量应用于科学和工程领域.分数阶微分用算子表示[21],其有多种定义,本研究中取Caputo 型分数阶微分算子,定义为式中:α 为阶次,m−1<α 分数阶微积分具有全局特性和记忆性,是初始点到终止点间所有状态信息的综合体现,其数值实现难度远超整数阶微积分.目前采用逼近方法以有限的整数阶状态信息近似出分数阶微积分数值[22].本研究使用频域滤波算法中Oustaloup 方法实现分数阶微积分数值计算,其本质是在限定频段内近似实现分数阶微积分算子,具有计算精度较高、运算简便的优点[23].考虑频带范围(ω1,ω2),构造Oustaloup 算法的滤波器传递函数为 式中:r为逼近后整数阶传递函数的阶数,为非负整数;频带范围 (ω1,ω2)=(0.001 rad/s,1 000 rad/s). 性质1Caputo 型分数微分算子用代换,即 当且仅当分数微分的下端t=z时,函数f(t)满足条件 性质2常数的Caputo 型分数微分 式中:r为任意常数. 性质3与整数阶微分类似,分数阶微分是一种线性运算,有 性质4Caputo 定义下的Laplace 变换为 趋近律是描述状态点运动至滑模面的速率,通过其可调节到达滑模面的时间及产生的冲击,可有效保证滑模控制的品质[24],是滑模控制中削弱抖振和改善控制动态性能的重要途径[25]. 1)等速趋近律 令ε=[sign(s1),sign(s2),···,sign(sn)]T,定义常量η为系统状态点到达切换面的趋近速率,表达式为 η值大小决定趋近速率快慢,η过大,则状态点将以较大的速度到达切换面,易引起较大抖振.si(t)为 切换函数,且,求解式(8)可得 2)指数趋近律 在等速趋近律基础上引入指数项 −τs,远离切换面时,主要体现为指数趋近;而到达切换面附近时,指数趋近速度锐减,此时等速趋近项 −ηε确保滑模变量在有限时间内到达切换面,即 求解式(10)得 3)幂次趋近律 状态点以幂次规律的趋近速率在有限时间内到达切换面,幂次项保证状态点接近滑动模态时减缓趋近速率,可有效削弱抖振,可得 对式(12)积分可得 经典滑模控制中符号函数导致控制器存在不连续切换,引起系统抖振[26],引入边界层法能够有效消除抖振[27].边界层法属于准滑动模态控制方法之一,准滑动模态控制使一定范围内的状态点被吸引至理想滑动模态的某一 µ 邻域内,µ 邻域称为滑动模态切换面的边界层[28].本研究采用饱和函数来替代符号函数,选取饱和函数 sat(si)为 式中:µ>0为 边界层厚度,i=1,2,···,n. 饱和函数与符号函数如图1 所示.在边界层内,采用连续控制;在边界层外,采用切换控制,从而削弱在滑模面上的抖振现象.令 ψ=[sat(s1),sat(s2),···,sat(sn)]T,构造饱和函数趋近律为 图1 饱和函数与符号函数Fig.1 Saturation function and sign function n关节机械臂系统的动力学方程为 令C=diag(c1,c2,···,cn),ci>0,系统误差e=qd−q,K=diag(k1,k2,···,kn),ki>0,则定义分数阶滑模面为 根据式(3)中给出的性质,可得 式(18)求导可得 合并式(15)和式(20)构造分数阶滑模控制律 利用李雅普诺夫稳定性理论进行稳定性分析,定义李雅普诺夫函数为 对于任意的s≠0都有V(t)>0.对式(22)求导,同时考虑式(20)可得 将式(21)代入式(23)中化简可得 根据饱和函数的定义可知sisat(si)≥0,因此,可得,即控制律满足稳定条件. 以含扰动的两自由度机械臂为仿真系统,为验证式(21)FOSMC 的控制律的控制效果,取对比控制律SMC 为,式(16)中系统动力学模型参数如下[29] 式中:质量参数m1=4kg,m2=2kg;长度参数l1=2 m,l2=1 m ;重力加速度g=9.8m/s2;扰动Δ(t)=3sin(2πt);期望轨迹q1d=cos(πt)和q2d=sin(πt);系统初始状态;控制器参数c1=c2=5,µ=0.9,η=0.5;仿真时长10s,仿真结果如图2和图3所示. 图2 轨迹跟踪Fig.2 Trajectory tracking 图3 轨迹跟踪误差Fig.3 Trajectory tracking error 图2中,选取α=0.2,两种控制方法均能实现对期望轨迹的跟踪,相比SMC,FOSMC的轨迹,更加接近期望轨迹. 轨迹跟踪误差如图3 所示.i=1,2为机械臂关节1 和2;j=1,2,3,4 为FOSMC 阶数α=0.2,0.4,0.6,0.8;ei和ei j分别为SMC和FOSMC轨迹跟踪误差.SMC和FOSMC 取不同阶次时系统到达稳态时间见表1.当 α=0.2时轨迹跟踪误差曲线能较快趋于平缓.两种控制方法的误差最终都趋于0,FOSMC 的误差收敛速度更快,即调整时间更短. 表1 系统到达稳态时间Table 1 System reaching steady state time 由图2 和图3 可知,两种控制方法均能实现对三角函数形式的期望轨迹的精确跟踪,与SMC 相比,FOSMC 的跟踪误差更小,能更快收敛于0,调整时间更短,具有更好的跟踪特性和稳定性. 针对两自由度机械臂系统,本研究基于经典滑模控制,引入分数阶微积分理论,构造一种新的分数阶滑模控制器.对滑模控制存在的抖振问题,采用饱和函数替代符号函数构造含边界层的滑模趋近律,利用李雅普诺夫直接法证明方法的稳定性.仿真结果表明,与经典滑模控制相比,新控制器具有更快的收敛速度和更好的控制性能.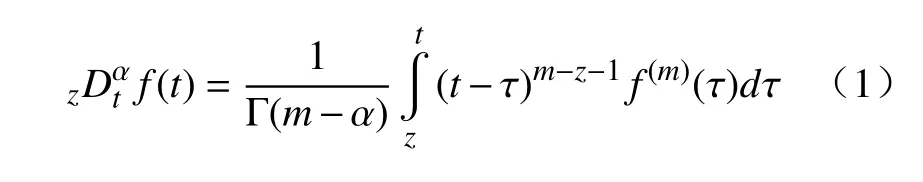
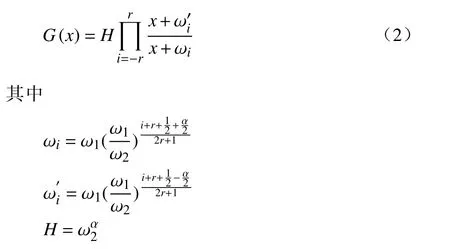
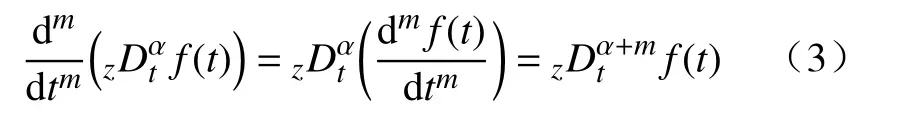
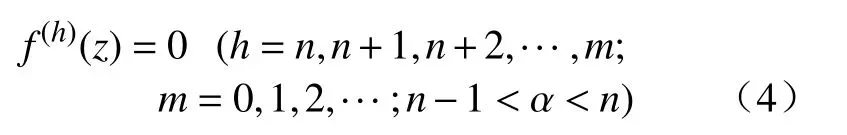

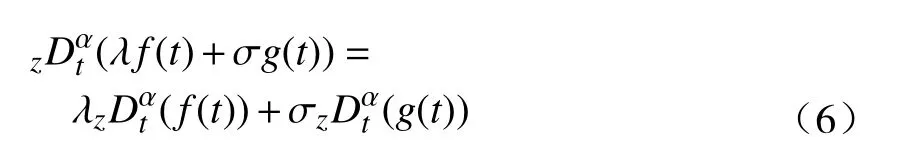
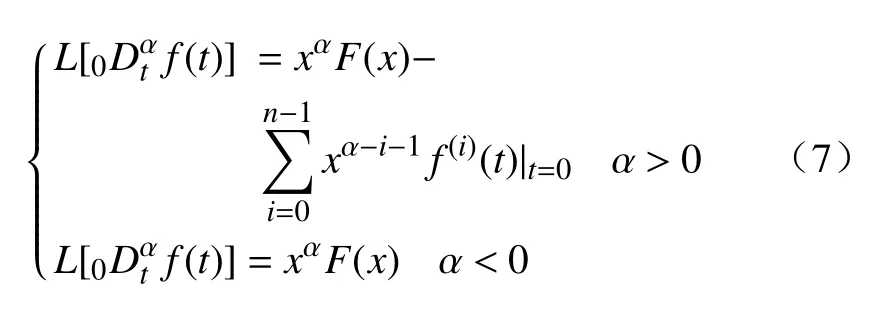
2 滑模趋近律
2.1 传统滑模趋近律

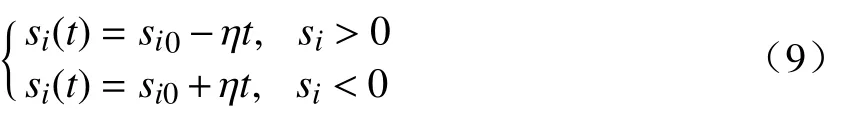
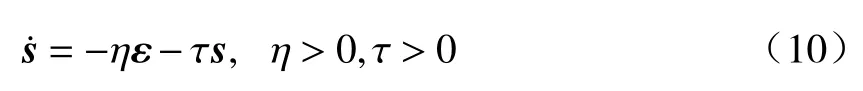
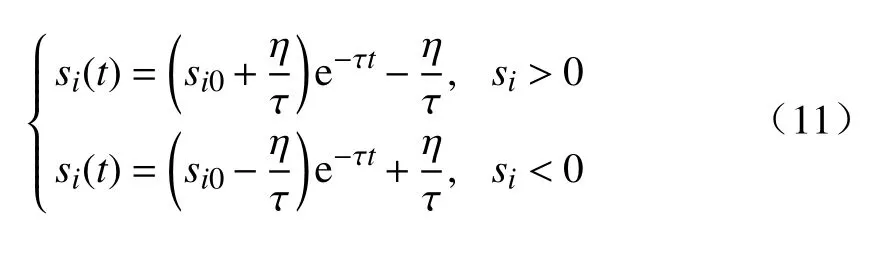
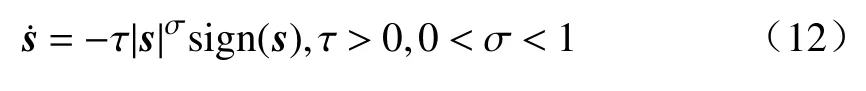
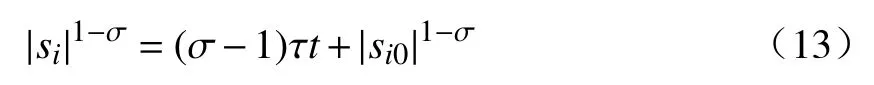
2.2 含边界层的滑模趋近律
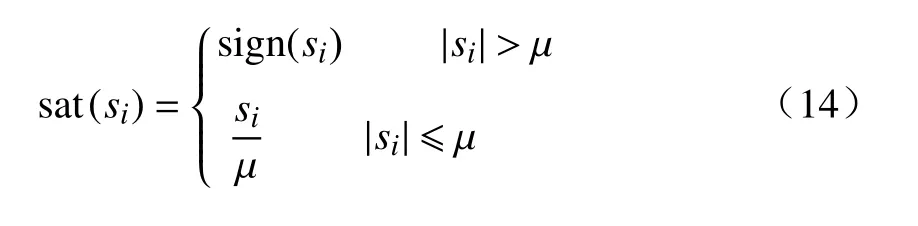

3 机械臂分数阶滑模控制
3.1 机械臂系统模型
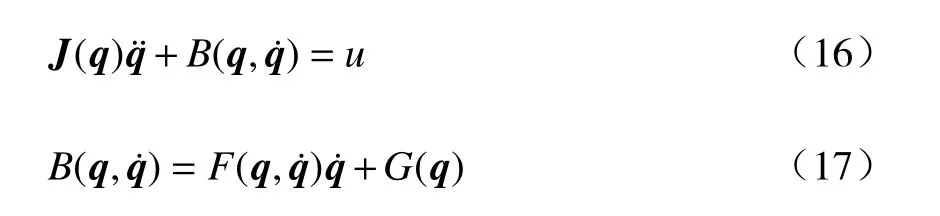
3.2 含边界层的分数阶滑模控制

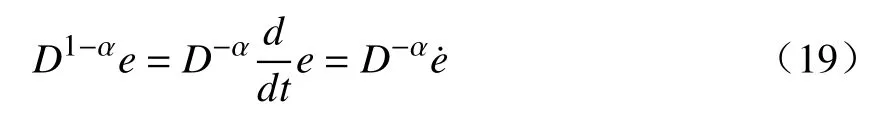
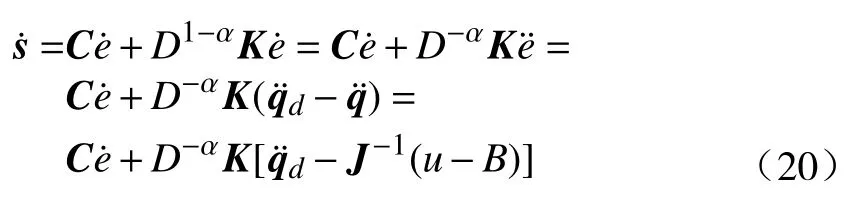
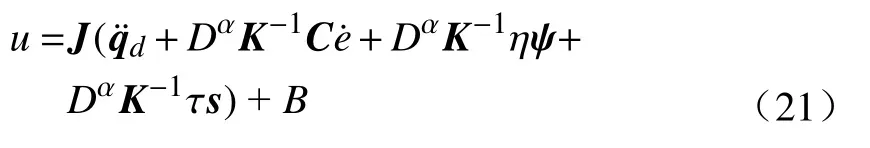

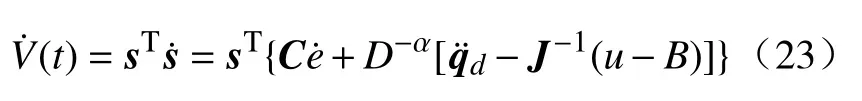
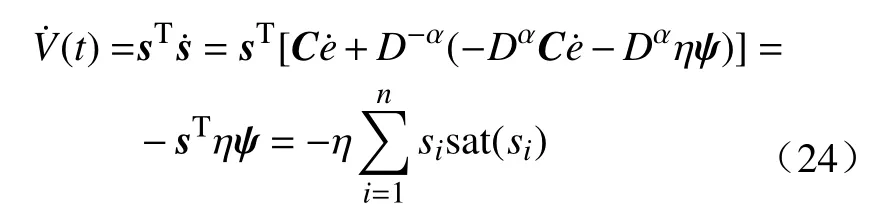
4 仿真算例

5 结语

