舰机双基地协同主动声探测范围分析
鞠建波,郁红波,单志超,杨少伟
(1.海军航空大学,山东 烟台 264000;2.中国人民解放军91388部队,广东 湛江 524000)
现代搜潜作战中,吊放声呐与航空浮标容易受平台噪声和海况等其他环境因素的影响,这将大大地降低探测到潜艇的概率[1-5]。双基地声呐的出现较好地解决了这一问题,通过将发射设备与接收设备分离,既避免了平台噪声的影响,又增加了探测距离。通过仿真计算,若要将平台噪声降低2 dB,双基地的等效半径将提高1.12倍。针对双基地声呐有效作用区域分析过程中模型较为简单的问题,本文提出了在目标强度不均匀的条件下双基地覆盖面积的计算方法,发现双基地覆盖面积随潜艇航向改变呈蝶形变化。同时本文通过仿真计算,得出了双基地优势区域内出现盲区的位置,并给出了在不同概略角情况下双基地的最佳配置。
文献[1]研究了如何优化双基地中浮标阵的使用,提高搜潜效率。文献[2]对双基地中声呐性能进行了分析。文献[3]研究了在海水吸收系数影响下舰机双基地覆盖面积的变化,计算了双基地的扩展面积比和扩展距离。文献[4]对比了在混响情况下单双基地的覆盖面积。文献[6]研究了目标强度均匀的情况下双基地的覆盖范围。文献[7-11]研究了多基地声呐系统传感器布设问题。文献[12]研究了多基地声呐探测范围的问题。以上文献在计算过程中为了简化模型,均认为目标强度在空间上是均匀的,但在实际情况下目标强度是不均匀的。通过本文的研究,可以对实际双基地的使用有一定的参考价值。
1 双基地的探测范围
图1为舰机协同双基地的工作原理,T为舰壳声呐,R为吊放声呐,S为潜艇目标,R1,R2分别为舰船,直升机距离目标的距离,β1,β2分别为潜艇相对于舰壳声呐与吊放声呐的方位角。本文考虑声呐工作时的噪声是海洋环境噪声。通过计算得出双基地工作的声呐方程为[2]
SLC+TS-(TL1+TL2)-(NL-DID)=DTD
(1)
其中,SLC是舰壳声呐的声源级,NL为海洋环境噪声,DID为吊放声呐指向性系数,DTD为吊放声呐检测阈。如图1所示,以舰船和基线中心为极点,基线为极轴建立极坐标系A、B。
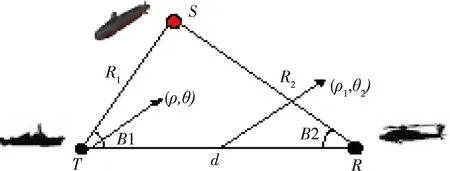
图1 双基地工作示意图
对于双基地,等效半径R=(R1R2)1/2,同时考虑球面损失和吸收损失的情况下,双基地等效半径表达式为
(2)
在双基地中,一旦舰船与吊放声呐的位置确定,目标点到两个定点的距离之积为定值,三者形成的图形为卡西尼卵形线。在极坐标系A中得出双基地极坐标方程,表达式为
ρ4-2ρ3dcosθ+d3ρ2=R4
(3)
假设海洋中的吸收系数α=2.194×10-4,舰壳声呐声源级SLC=230 dB,海洋环境噪声NL=60 dB,吊放声呐指向性指数DID=18 dB,检测阈DTD=15 dB。为简化模型,假设目标强度是均匀的,TS=15 dB。dg为分置系数,是基线距离与等效半径的比值,dg取值0~2.5。图2为双基地覆盖范围随基线距离的变化趋势。
从图2中,可以看出双基地覆盖面积随基线距离改变而改变,当dg=0时,双基地的面积为等效半径组成圆的面积。当dg=1.4,卵形线开始发生扭曲,从基线中心向内凹陷,当分置系数dg≥2.0时,卵形线分裂成两个不相连的区域。
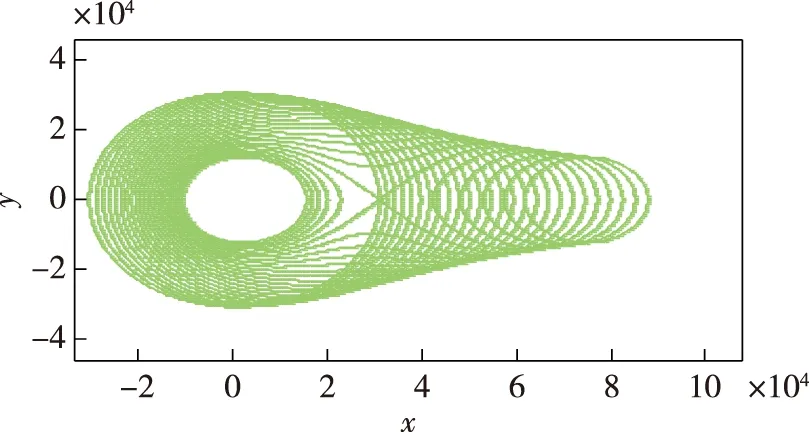
图2 基线距离改变双基地覆盖范围示意图
潜艇在航行过程中,目标强度并不是均匀的,而是随着潜艇航向β改变的(如图3),满足经验公式[5]
TS=25(16.17-3.98cos(2β)-3.083cos(6β))/
23.233
(4)
航向角取-180°~180°,可以得出双基地覆盖范围随航向角变化的趋势图。
如图4所示,声呐位置不发生改变时,随着潜艇航向的改变,双基地覆盖面积随着目标强度的规律发生改变。当潜艇东西航向时,目标强度最大,双基地覆盖面积也最大,潜艇南北航向时,目标强度最小,这时双基地覆盖面积也是最小。说明双基地的覆盖面积不但受基线距离的影响,也受潜艇航向角的影响。
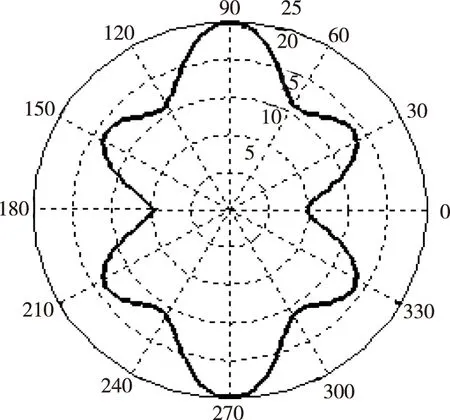
图3 潜艇目标特性图
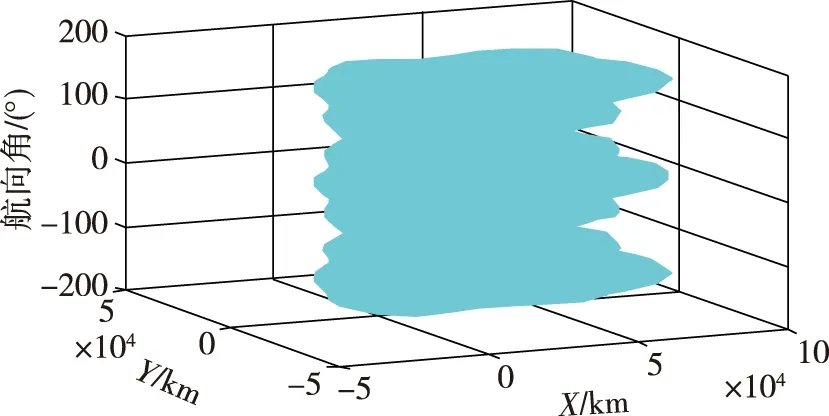
图4 双基地覆盖范围随航向角变化仿真图
2 优势区域与盲区
在极坐标系B中,可以得出双基地的面积Ab的表达式为
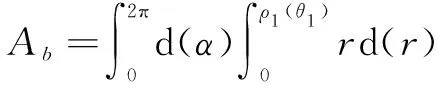
(5)
根据三角关系,可以得到积分因子ρ1的表达式

(6)
在极坐标系A中由三角关系可以得出极径ρ的表达式
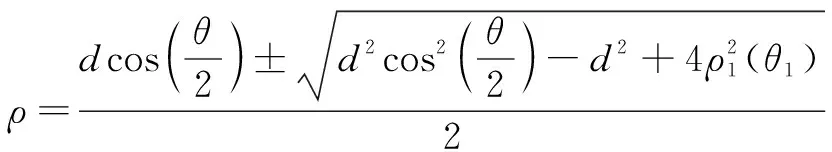
(7)
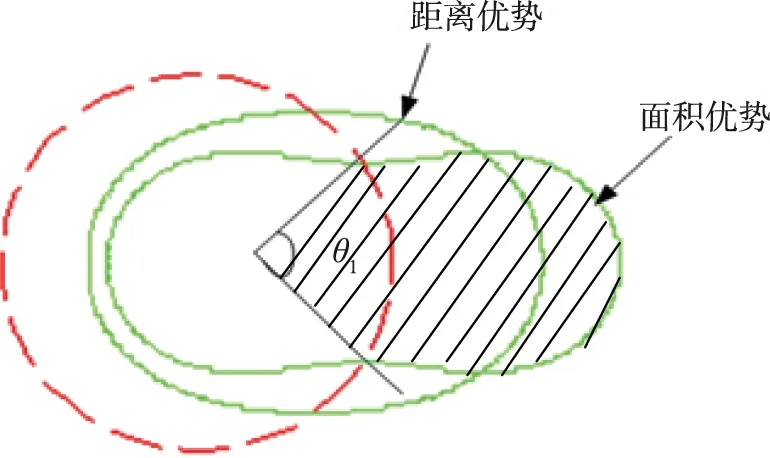
图5中,红色区域为当d=0时,半径为等效半径R时的探测范围,也称为等效合置圆。从图5中可以看出,在全方位的情况下,双基地的探测面积总是小于等效合置的面积,但是在沿着极轴的方向,在一定的角度上双基地存在着距离优势和面积优势,这个角度统称为优势角,记为α,优势角内的双基地的面积称为优势区域,记为A2。在优势区域内,双基地有更大的覆盖范围,因此在一定角度内搜潜时,双基地优势将大大增加。

图5 优势区域示意图
由极径ρ的表达式,可以求出优势区域面积的表达式为
(8)
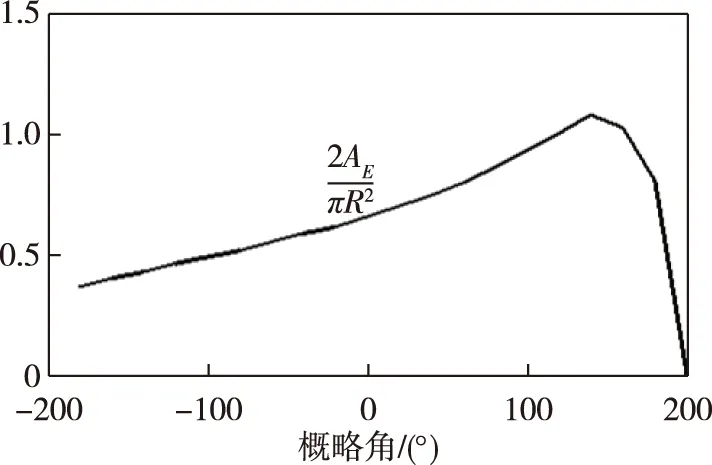
画出优势区域面积随分置系数的图形,分别用等效合置面积A和在优势区域内等效合置的面积Aα归一化,其中A=πR2,Aα=(α/2)·R2,可以看出双基地的面积在分置系数dg<1时,与等效合置的面积大致相等。但当dg>1时,双基地的面积开始小于等效合置的面积,说明双基地在全方位的情况下相对于单基地并不具有优势。在优势区域内,双基地的面积相对于等效合置圆的面积随着分置系数的增加不断增加,说明在一定的警戒角内,双基地不但具有距离上的优势,面积也有很大的优势,这大大提高了探测到潜艇的概率。比较图见图6。
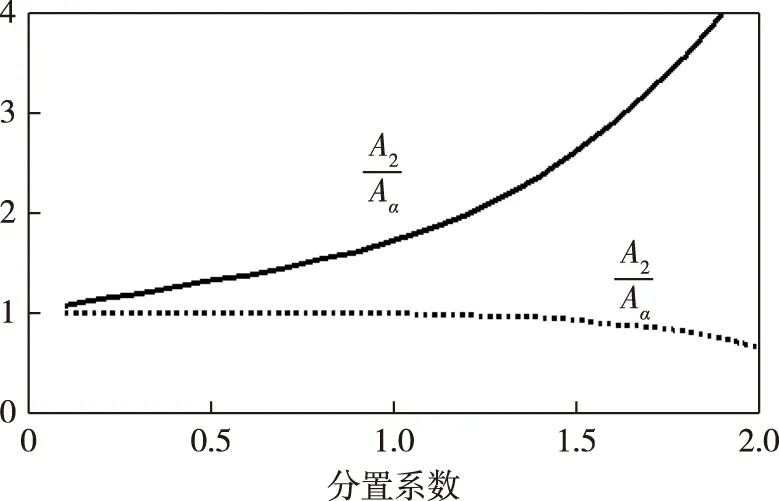
图6 优势区域内探测范围比较示意图
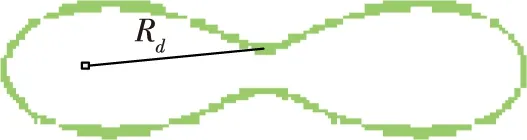
随着分置系数的不断增加,卵形线会发生向内凹陷,这个时候优势区域会发生盲区,盲区的产生是由于卵形线的不断凹陷,造成双基地无法覆盖的一部分区域。如图7黑色区域所示,当分置系数dg≥2时,卵形线分裂成两个不相连的区域,舰壳声呐与吊放声呐失去联系,优势区域消失,所以双基地使用是有限制条件的,当dg≥2时双基地的优势将不复存在。
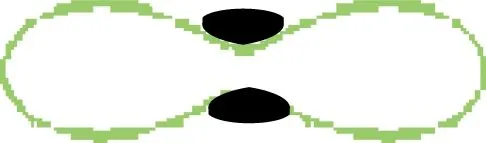
图7 盲区示意图
根据几何关系,优势区域的面积可以简化为下列表达式
(9)
但当优势区域中出现盲区后,此公式便不适用,因为A′2总是小于A2,所以求出卵形线何时出现盲区,可以帮助简化计算过程,提高搜潜效率。画出优势区域面积示意图,用A′2进行归一化。当分置系数dg=1.88时,归一化的值开始小于1,A2 通过图8可以看出,当目标强度为定值时,双基地盲区出现时的分置系数是确定的。图3已经说明潜艇的目标特性呈蝶形变化,双基地的等效半径也不断变化。但通过图9可以看出,不管潜艇的航向角如何变化,双基地均会在dg=1.88时出现盲区,说明双基地的盲区出现与潜艇航向无关,与潜艇目标强度不均匀也无关。 图8 盲区出现时分置系数图 图9 盲区出现时分置系数随潜艇航向变化示意图 通过第2节可以发现,双基地在一定的角度内相对于等效合置圆来说具有距离优势和面积优势,但是随着距离优势的增加,面积优势开始不断减少,两种优势不可兼得,应根据实际作战环境、战场情况来确定需要哪种优势,达到预想的目的。 潜艇被发现后会在一定概略角内进行逃逸,以概略角θ1=60°为例,在概略角内,随着基线距离的改变,双基地优势角α也发生改变,概略角内的双基地面积AE也发生变化,如图10。AE与优势角α的表达式如下: (10) (11) 图11所示的是概略角内面积AE随分置系数dg变化的仿真图。图内的纵坐标为概略角内双基地的面积AE与等效合置圆面积的一半A/2的比值。从图中可以看出,当分置系数dg=1.7时,概略角内双基地面积AE最大。 图10 概略角内面积随分置系数变化仿真图 图11 双基地探测范围中最短探测距离示意图 图12 概略角内最短探测距离随分置系数仿真图 从3.1节和3.2节可以知道当概略角θ1=60°时,面积优势和距离优势对应的分置系数分别为dg=1.7和dg=1.2,两种优势配置如图13所示。 图13 两种优势的双基地配置 通过概略角θ1=60°得到延伸,可以计算出概略角θ1∈(20°,180°)下,距离优势和面积优势的分置系数,如图14所示。 图14 不同概略角下两种优势随分置系数趋势图 本文讨论了目标强度不均匀情况下双基地的覆盖范围。研究发现,当潜艇航向发生变化时双基地覆盖范围也呈现蝶形变化,说明双基地覆盖范围随潜艇航向改变而改变。双基地声呐的覆盖范围在全方位的情况下并不是优于等效合置声呐的作用范围,而是在特定角度内具有优势,不但有距离优势还有面积优势。计算出了优势区域内盲区出现时分置系数的大小。通过概略角内面积优势与距离优势的比较,得出了不同的双基地配置方案,对后期舰机协同作战有一定的参考意义。 本文假设声呐在工作时只受海洋环境噪声的影响,但现实作战中要受到噪声与混响的共同作用,所以在噪声和混响影响下的双基地覆盖面积有待进一步研究。

3 双基地的最优配置
3.1 面积优势

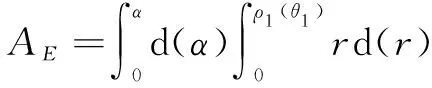
3.2 距离优势
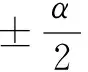

3.3 双基地的最优配置
4 结束语

