高重合度直齿轮刚度及最大载荷分担率的影响分析*

范士超，李发家，崔焕勇*，吴伟，张少运

高重合度直齿轮刚度及最大载荷分担率的影响分析*

范士超1，李发家1，崔焕勇1*，吴伟2，张少运2

（1.济南大学 机械工程学院，山东 济南 250022；2.山东蒙沃变速器有限公司，山东 临沂 276000）

针对高重合度外啮合齿轮，在考虑轮齿弹性变形的前提下，研究了外啮合高重合度外啮合渐开线直齿圆柱齿轮副的轮齿变形、刚度及最大载荷分担率在轮齿参数变化时的变化规律。研究表明：在给定参数变化范围内，单对齿刚度最大值随齿顶高系数的增大减少9.5%，随压力角的增大增加44.1%，随齿数的增多增加8.1%，随变位系数的增大增加29.2%；在给定高重合度参数变化区间内，多齿啮合刚度的最大值随齿顶高系数的增大减少6.8%，随压力角的增大增加22.7%，随齿数的增多增加12.1%，随变位系数的增大增加8.5%；在给定高重合度参数变化区间内，最大载荷分担率随齿顶高系数的增大从60.45%近似线性减小到57.88%，最大载荷分担率随压力角的增大从53.27%近似线性减小到61.41%，最大载荷分担率随齿数的增多从59.56% 近似反比例曲线降低到56.00%，最大载荷分担率随变位系数的增大从52.41%近似线性增大到61.19%。

高重合度；直齿轮；刚度；载荷分担率；变形

前言

直齿轮圆柱齿轮具有经济性好、支撑结构简单、啮合时系统无轴向力等优点，使其在汽车、航空等领域结构优化中应用广泛[1-2]。随着汽车、航空、航天等行业的飞速发展，对传动系统提出了更高的要求，低重合度（LCR：Low Contact ratio，重合度<2）直齿轮很难满足汽车、航空、航天等行业需要。对此部分学者提出将重合度大于2的直齿圆柱齿轮称之为高重合度（HCR：High Contact Ratio）齿轮，啮合齿数增多，齿轮的参数使齿轮刚度和载荷分配发生变化，合理的参数设计使齿间载荷分配得到优化，最大载荷分担率降低，指导齿轮的接触强度、弯曲强度、胶合强度等的设计[3-4]，有必要对HCR直齿轮的刚度及齿间载荷分的影响规律进行研究。

GB3480和ISO6336[5-6]都给出了齿轮刚度和齿间载荷分配的简化计算公式，但由于多数采用近似的经验系数，使刚度及载荷分配的计算误差较大，很难满足高精度的设计要求； Zhou Xiaojun等[7]将轮齿简化为变截面悬臂梁，提高了齿轮刚度计算精度；王志钦等[8]通过数值仿真计算了齿轮变位对LCR齿轮刚度的影响；王晓鹏等[9]基于几何学和势能法提出一种计算直齿轮副的精确建模方法；张波波等[10]基于有限元法计算了齿数对单齿刚度及时变啮合刚度的影响；王龙宝[11]利用石川法研究了齿轮齿数对单齿刚度、单齿副刚度和平均刚度的影响；李发家[3]通过能量法研究了齿顶高系数、压力角和变位系数对刚度的影响但未涉及最大载荷分担率的影响研究；对于多齿啮合时变啮合刚度的变化将直接影响齿轮的齿间载荷分配，改变最大载荷分担率的大小，进而影响齿轮的承载能力。Sánchez[12]基于最小弹性势能准则建立了外啮合齿轮的载荷分布模型；Miryam B. Sánchez[13]给出了考虑接触挠度的啮合刚度近似方程，并计算了齿间载荷分配；Arafa and Megahed[14]通过有限元的方法，研究了LCR直齿轮啮合齿间的载荷分担情况，得出单齿沿啮合线载荷循环规律；邓效忠等[15]通过静力学分析，得出HCR齿轮最大载荷分担率约占60%；Thirumurugan[16]采用有限元法，分析了压力角对 HCR 外啮合齿轮齿间载荷分配的影响。

综上所述，国内外对低重合度齿轮刚度及齿间载荷分配研究较多，对HCR直齿圆柱齿轮单对齿刚度、多齿啮合刚度及最大载荷分担率的影响规律研究较少，刚度及最大载荷分担率对齿轮的强度计算有较大的影响。因此，本文主要利用材料力学的方法，研究齿轮在参数变化时轮齿单对齿刚度、多齿啮合刚度及最大载荷分担率的变化规律，为齿轮的参数优化设计提供理论依据。

1 齿轮的刚度及最大载荷分担率的计算

轮齿的刚度为使一对或多对齿同时啮合的齿轮在每单位齿宽上产生单位挠度所施加的载荷，单位齿上的载荷为：

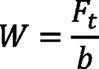
齿轮的挠度为：

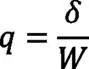
则轮齿的刚度为：

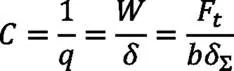
式中，为齿宽；F为轮齿所受载荷；δ为轮齿的总变形量。

齿轮的总变形量包括弯曲变形δ、剪切变形δ、压缩变形δ、基体变形δ、接触变形δ等，轮齿的总变形可表示为：

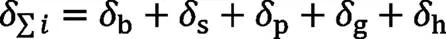
在齿轮啮合过程中，仅考虑一对轮齿啮合时所对应的刚度为单对齿刚度，HCR直齿轮正常啮合时对应的刚度为多齿啮合刚度。本文采用能量法，将轮齿简化成变截面悬臂梁，如图1[3]，通过参数化齿轮的方程，求解轮齿各点的受力变形。根据文献[3]给出的变形公式计算微单元i在任意载荷作用下的变形。

如图2齿轮啮合示意图，三齿啮合时，载荷F由三齿共同承担。

图2 HCR齿轮啮合示意图

双齿啮合时：

通过将轮齿简化成串联弹簧可得单对齿刚度，齿对AD、齿对BE、齿对CF的刚度C、C、C为：

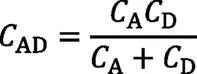
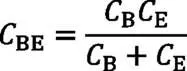
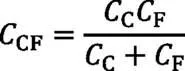
通过计算齿轮啮合时啮合点所对应齿廓上的位置，结合单对齿刚度，通过啮合齿对啮合线方向的变形相同求得多齿啮合刚度。利用啮合点处变形δ乘以多齿啮合刚度计算出齿对承担的载荷，并算出载荷分担率。

2 HCR直齿轮的参数的设计

表1 外啮合齿轮副参数

图4 变位系数对重合度的影响

以文献[3]中的LCR齿轮副参数为例，如表 1。重合度受齿顶高系数h*、压力角、齿数、变位系数的影响。通过图3、图4计算结果所示，当h*≥1.02、<24.5°时，重合度大于2，当变位系数取-0.5~-0.45时，齿轮才满足HCR要求，可看出压力角、齿顶高系数影响显著。

得出HCR齿轮的参数设计范围，如表2所示。

表2 齿轮设计参数变化范围

3 齿轮几何参数对变形、刚度及最大载荷分担率的影响分析

3.1 齿顶高系数ha*对变形、齿轮刚度及最大载荷分担率的影响规律

在不计加工误差时，仅改变h*大小，当h*≥1.25时，重合度>2。当F=1000N，h*取1.2、1.26、1.3、1.35、1.4时，齿轮的变形、刚度及最大载荷分担率的关系曲线如图5 （a）、图5（b）所示。

图5（a） 不同齿顶高系数下变形、刚度、最大载荷分担率在啮合线上的分布

图5（b） 最大载荷分担率随齿顶高系数的变化曲线

主动齿轮的啮合从齿根啮入齿顶啮出，可以看出随着齿顶高系数的增大，靠近齿根处的初始啮合点的变形略有增大，齿顶变形增大较为明显；齿顶高系数h*=1.4时，对比h*=1.2，单对齿刚度最大值约减小9.5%，最小值约减小21.2%，多齿啮合刚度最大值约增大15.7%，最小值约增大56.6%，这是由于重合度增加，齿轮由LCR变为HCR所致，相比LCR，HCR齿轮多齿啮合刚度波动小，啮合平稳；在HCR范围内，多齿啮合时变刚度最大值、最小值均随齿顶高系数的增加而降低，齿顶高系数h*=1.4时，对比h*=1.26，多齿啮合刚度最大值约减小6.8%，最小值约减小3.7%，最大载荷分担率变小，从占60.45%减小到57.88%，且变化近似线性。

3.2 压力角α对变形、刚度及最大载荷分担率的影响规律

仅改变表1中α值不易使齿轮达到HCR范畴，故同时取h*=1.3，<21.45°时，>2。α取14°、16°、18°、20°、22°时，齿轮的变形、刚度及最大载荷分担率的关系曲线如图6（a）、图6（b）所示。

由图6（a）可以看出，随压力角的增大，靠近齿根处的初始啮合点的变形减小，齿顶变形也减小，变形变化曲线斜率增大；压力角=22°时，对比=14°，单对齿刚度最大值约增大44.1%，最小值约增大26.3%，多齿啮合刚度最大值基本没变，最小值约减小22.5%，这是由于随压力角的增大，齿轮从LCR变为HCR所致。

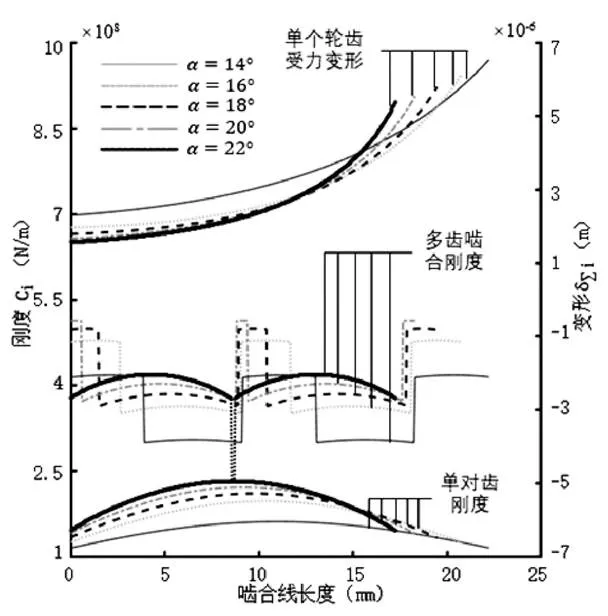
图6（a） 不同压力角下变形、刚度、最大载荷分担率在啮合线上的分布

图 6（b） 最大载荷分担率随压力角的变化曲线

在HCR范围内，多齿啮合刚度最大值、最小值随压力角的增大而增大，压力角=20°时，对比=14°，多齿啮合刚度最大值约增大22.7%，最小值约增大24.1%，最大载荷分担率变大，在压力角从=14°增大到=21.45°时，从53.27%减小到61.41%，且变化近似线性。

3.3 齿数Z对变形、刚度及最大载荷分担率的影响规律

仅改变表1中的Z，齿轮达不到HCR，故取h*=1.3，其余参数参照表1，Z取29、90、150、200、300时，齿轮的变形、刚度及最大载荷分担率的关系曲线如图7（a）、图7（b）所示。

由图7（a）、图7（b）可以看出，随齿数的增加，靠近齿根处的初始啮合点的变形和齿顶变形略微减小，齿顶变形增大，变形变化曲线斜率减小；

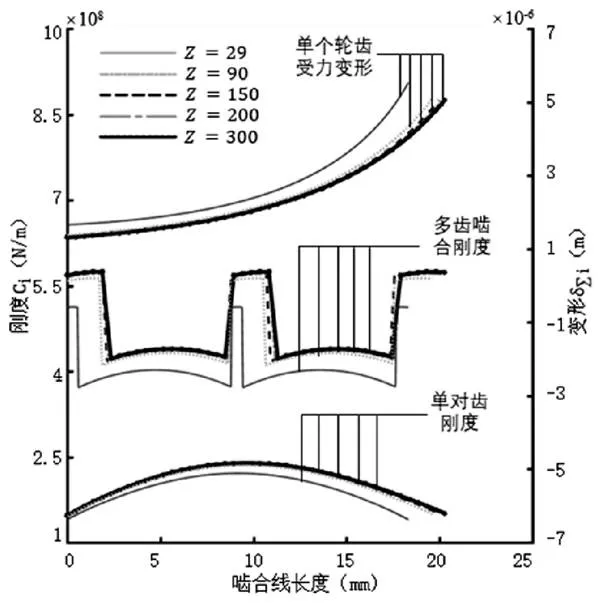
图7（a） 不同齿数下变形、刚度、最大载荷分担率在啮合线上的分布

图7（b） 最大载荷分担率随齿数的变化曲线

齿数Z=300时，对比Z=29，单对齿刚度最大值约增大8.1%，最小值约增大5.4%，多齿啮合刚度最大值约增大12.1%，最小值约增大13.7%，最大载荷分担率变小，随齿数的增加，从59.56% 降低到56.00%，变化趋势近似反比例曲线。

3.4 变位系数x对变形、刚度及最大载荷分担率的影响规律

标准齿轮副仅通过改变变位系数不易达到HCR，故取h*=1.3，当1=2<0.11时，>2，取-0.5、-0.3、-0.1、0.1、0.2时，齿轮的变形、刚度及最大载荷分担率的关系曲线如图8（a）、图8（b）所示。

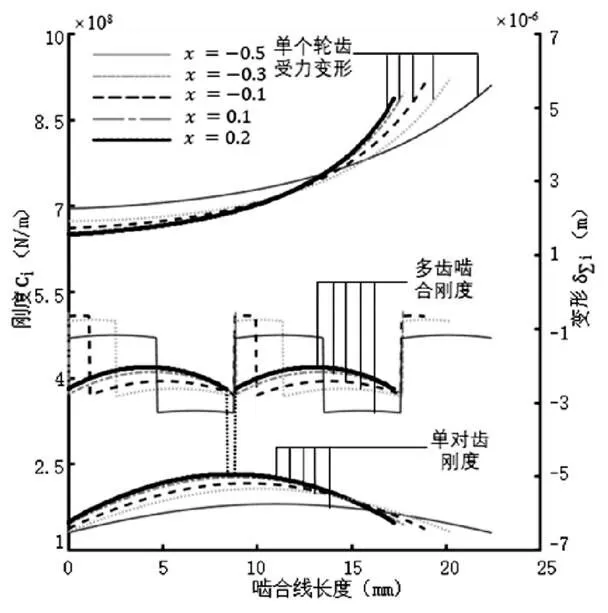
图8（a） 不同变位系数下变形、刚度、最大载荷分担率在啮合线上的分布

由图8（a）、图8（b）可以看出，随着变位系数的数值不断增大，靠近齿根处的初始啮合点的变形减小，齿顶变形也减小，变形变化曲线斜率增大；变位系数2=0.2时，对比2=-0.5，单对齿刚度最大值约增大29.2%，最小值约增大13.8%，多齿啮合刚度最大值约减小11.7%，最小值约减小31.5%，这是由于变位系数数值的增大，齿轮从HCR转变为LCR所致；在HCR范围内，多齿啮合刚度最大值、最小值随变位系数的增大而增大，变位系数2=0.1时，对比2=-0.5，多齿啮合刚度最大值约增大8.5%，最小值约增大9.6%，最大载荷分担率变大，在变位系数从2=-0.5增大到2=0.11时，从52.41%增大到61.19%，且变化近似线性。

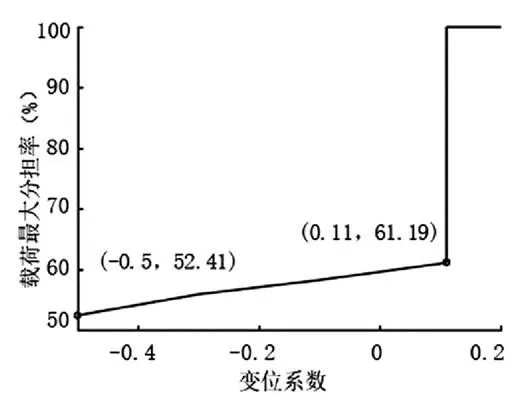
图8（b） 最大载荷分担率随变位系数的变化曲线

4 结论

本文针对HCR渐开线直齿圆柱齿轮，研究了齿轮参数对单个轮齿受力变形、单对齿刚度、多齿啮合刚度及多齿啮合时的最大载荷分担率的影响，得出以下结论：

1）当h*从1.2增大到1.4时，由于轮齿的增长，单齿受力变形在齿顶处明显变大，单对齿刚度最大值、最小值减小9.5%、21.2%，在HCR范围内，h*从1.26增大到1.4时，多齿啮合刚度的最大值最小值减小6.8%、3.7%，最大载荷分担率从60.45%减小到57.88%，且变化近似线性。

2）当从14°增大到22°时，轮齿齿根变厚齿顶变尖，初始啮合点、齿顶的变形均减小单对齿刚度最大值、最小值增大44.1%、26.3%，在HCR范围内，从14°增大到20°时，多齿啮合刚度最大值、最小值增大22.7%、24.1%，最大载荷分担率在从14°增大到21.45°时，近似线性的从53.27减小到61.41。

3）当齿数从29增大到300时，齿轮啮合线变长，初始啮合点、齿顶的变形均减小，单对齿刚度最大值、最小值增大8.1%、5.4%，多齿啮合刚度最大值最小值增大12.1%、13.7%，最大载荷分担率以近似反比例曲线关系从59.56% 降低到56.00%。

4）当变位系数从-0.5增大到0.2时，初始啮合点、齿顶的变形均减小，单对齿刚度最大值、最小值增大29.2%、13.8%，在HCR范围内，变位系数从-0.5增大到0.1时，多齿啮合刚度最大值、最小值增大8.5%、9.6%，最大载荷分担率在变位系数从-0.5增大到0.11时，近似线性的从52.41%增大到61.19%。

[1] 李发家.高重合度行星齿轮传动系统强度及动力学研究[D].南京航空航天大学,2015.

[2] 渠珍珍,鲍和云,朱如鹏,等.高重合度行星齿轮传动系统动态特性分析[J].机械科学与技术, 2012, 31(7):1174-1179.

[3] 郭梅,梁作斌,陈聪慧. HB与ISO标准中渐开线圆柱齿轮胶合承载能力计算标准比较[J].燃气涡轮试验与研究,2018,31(1):59-62.

[4] 罗彪.齿轮传动系统热弹耦合动力学及轮齿多目标综合修形研究[D].北京科技大学, 2019.

[5] GB 3480-1997,渐开线圆柱齿轮承载能力计算方法, 1997.

[6] ISO 6336,Calculation and load capacity of spur and helical gears, 2006.

[7] Zhou Xiaojun, Shao Yimin, Lei Yaguo, et al. Time-Varying Meshing Stiffness Calculation and Vibration Analysis for a 16DOF Dynamic Model With Linear Crack Growth in a Pinion[J].ASME J Vib Acoust,2011, 134(1): 011011-1-011011-11.

[8]王志钦,王晓笋,王施茹,巫世晶.齿轮变位对啮合刚度影响的数值仿真[J].机械传动,2020,44(04):80-84.

[9]王晓鹏,刘世军,李纪强.基于几何学和势能法的直齿轮副时变啮合刚度精确建模及应用[J].机械传动,2020,44(03):91-96.

[10]张波波,蔡丽,方杰,郑媛,汪涛,熊杨寿.基于有限元法的齿轮时变啮合刚度计算方法研究[J].机械传动,2019,43(11):74-77+83.

[11] 王龙宝.齿轮刚度计算及其有限元分析[D].江苏大学,2007.

[12] M.B. Sánchez, M. Pleguezuelos, J.I. Pedrero. En-hanced model of load distribution along the line of contact for non-standard in-volute external gears. Meccanica 48 (2013) 527-543.

[13] Miryam B.Sánchez, Miguel Plegue-zuelos, José I. Pedrero. Appro -ximate equations for the meshing stiffness and the load sharing ratio of spur gears including hertzian effects. Mechanism and Mach -ine Theory, 2017, Volume 109, Pages 231-249.

[14] M.H.Arafa,M.M.Megahed. Evaluation of spur gear mesh complian -ce using the finite element method[J]. Pro-ceedings of the Institu -tion of Mechanical Engineers, 213 (part C) (1999).

[15] 邓效忠,方宗德,魏冰阳,等.大重合度齿轮的性能研究[J].航空动力学报,2003,1(6):744-748.

[16] Rama1 Thirumurugan,G. Muthuveerappan.Critical loading points for maximum fillet and contact stresses in normal and high contact ratio spur gears based on load sharing ratio[J]. Mechanics Based Design of Structures and Machines, 2011, 1(39):118~141.

Influence Analysis of Stiffness and Maximum Load-Sharing Ratio of High Coincidence Spur Gear*

Fan Shichao1, Li Fajia1, Cui Huanyong1*, Wu Wei2, Zhang Shaoyun2

（1.School of Mechanical Engineering, University of Jinan, Shangdong Jinan 250022; 2.Shandong MENWO Transmission Limited Company, Shangdong Linyi 276000）

Under the premise of considering the elastic deformation of gear teeth, the variation rule of tooth deformation, stiffness and maximum load sharing rate of HCR involute spur gear was studied when tooth parameters change. Within a given parameter range, the maximum stiffness of single pair of teeth decreased by 9.5% with the increase of the addendum coefficient, increased by 44.1% with the increase of the pressure angle, increased by 8.1% with the increase of the number of teeth, and increased by 29.2% with the increase of the modification coefficient.Within a given parameter range of high contact ratio, the maximum mesh stiffness of multiple teeth decreased by 6.8% with the increase of the addendum coefficient, increased by 22.7% with the increase of the pressure angle, increased by 12.1% with the increase of the number of teeth, increased by 8.5% with the increase of the modification coefficient, Within a given parameter range of high contact ratio, maximum load share ratio increases with the addendum coefficient approximate linear decrease from 60.45% to 57.88%, with the increase of pressure angle approximate linear decrease from 53.27 to 61.41, with the increasing of the number of teeth approximate inverse curve is reduced to 56.00% from 59.56%, with the increase of modification coefficient approximate linear increase from 52.41% to 61.19%.

High contact ratio;Spur gear;Stiffness;Maximum load sharing rate;Deformation

10.16638/j.cnki.1671-7988.2021.04.034

TH132.417

A

1671-7988(2021)04-111-05

TH132.417

A

1671-7988(2021)04-111-05

范士超（1996-），硕士，就读于济南大学机械工程学院，专业：先进制造技术与装备。

崔焕勇，就职于济南大学机械工程学院。

山东省重点研发计划 2019GGX104028；国家青年基金 51605191。