浑天说数理模型的构建尝试与失败——以祖暅《浑天论》为中心

邓可卉 李淑浩

(东华大学 人文学院， 上海 200051)

两汉及魏晋南北朝时期是中国古代关于宇宙理论探讨最为活跃的时期。东汉蔡邕说“论天体者三家，宣夜之学，绝无师法。周髀数术具存，考验天状，多所违失。唯浑天仅得其情，今史官所用候台铜仪，则其法也”[1]，此话有一定深意，历史上曾经存在三种宇宙学说鼎立的局面，其中尤以浑天说和盖天说的争论最为激烈，出现了像扬雄这样的大儒由一个盖天家转而支持浑天说，并提出“难盖天八事”的极端事例。盖天说有《周髀》为证，数术俱存，浑天说虽然仅得其情，但是在争论中并没有占有足够的优势。究其原因，主要是由于它没有一套数理模型支持。然而，历史真的是这样吗？通过释读被辑入《开元占经》①《开元占经》卷1“天体浑宗”记录了从张衡到刘焯时期浑天说的相关论述，包括许多在正史中没有记录的史料。作者将它们与《晋书》、《隋书》中的相关内容比对，最后选择《开元占经》为本文许多原始文献的出处。的祖暅(1)一般认为，祖暅原名“祖暅之”，以《南史·冲之传(七二)》中的记录为证。但后世记录中，包括本文所引《隋书·天文志》、《开元占经》等文献中都用“祖暅”，这些文献距离祖暅生活年代也就一百多年，说明了至少在唐代早中期就开始使用这一名字。另外，当代中古史专家罗继祖先生在1987年撰文《祖暅之》考证了宋代以后一些重要文献使用“祖暅”名称，认为后人遂以“不误之误”采纳之。基于上述理由，本文在此处及下文的论述中采用“祖暅”一名。的《浑天论》一卷，我们发现祖暅在尝试构建浑天说数理模型方面做出了一系列工作，与《周髀算经》中盖天说数理模型有所照应，这为我们解构浑天说数理模型提供了若干理路。

然而，陈美东认为，中国古代的诸多宇宙学说大多缺乏明确的数学模型，而盖天说是一个例外。[2]他的观点代表了学术界对汉以后宇宙论的普遍认识。江晓原曾对浑天说和盖天说做出评价，认为浑天说只是用文字叙述出来了一个“浑天”的大致图像，既无明确的结构，也没有具体的数理，并不是一种宇宙的几何模型。[3]但他又指出只有浑天说可以和此后2000年中国的数理天文学相容。[4]曲安京则认为，中国古代历法缺乏一个明确的宇宙模型的支持，且古代数理天文学对宇宙模型的理论构建并不特别在意。[5]三位的观点在学术界具有代表性。这说明，关于历史上构建浑天说数理模型的尝试与失败原因至今没有受到学术界重视，特别是祖暅的浑天论学说未受到足够关注。

依据“从张衡到祖暅，前后四百年，可以说是浑天说的全盛时期”的说法[6]，本文以张衡到祖暅约400年间浑天说的发展为线索，详细讨论历史上构建浑天说数理模型的尝试与失败的过程。

1 张衡初建浑天说数理模型

浑天说在西汉落下闳时代就已出现[7]，遗憾的是，相关的具体论述并没有传世。直到东汉时期，张衡才首次对浑天说进行了系统的阐述。在《浑仪注》(2)关于《浑仪注》是否为张衡所作的问题，学术界曾有过激烈的争论。参见陈久金先生的论文《〈浑天仪注〉非张衡所作考》和陈美东先生的论文《张衡〈浑天仪注〉新探》。综合两位学者的研究，本文认为《浑仪注》系张衡所著。中，张衡指出“周旋无端，其形浑浑，故曰浑天也”[8]，“浑”用来形容天的形状，即天是一个球体。该书还记载了浑天说天地结构，共有以下六条：

(1)浑天如鸡子，天体圆如弹丸，地如鸡子中黄；(2)周天三百六十五度四分度之一，又中分之，则一百八十二度八分之五覆地上，一百八十二度八分之五绕地下；(3)两端谓之南北极。北极，乃天之中也，在正北，出地上三十六度；南极，天之中也，在南入地三十六度，两极相去一百八十二度半强；(4)赤道横带天之腹，去南北二极各九十一度十六分度之五；(5)黄道斜带其腹，出赤道表里各二十四度；(6)夏至去极六十七度而强，冬至去极百一十五度亦强。[8]

学术界对上述第(1)条的讨论主要包括地是球形[9]、半球形[10]还是平面形([6]，36- 41页)三种观点。目前看来，由于前两种观点在古代数理天文学中未得到验证，所以，张衡浑天说中“地平”说法更加可信，这也是我们下文讨论浑天说数理模型的一个重要前提。

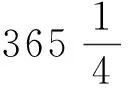
但是在汉至魏晋南北朝时期中国古代宇宙论激烈争论的背景下，浑天说仅有以上数据是不够的。与浑天说对立的《周髀算经》盖天说冬至日道径47.6万里，此数再加上两个日照四旁16.7万里，得到四极径为81万里，周长为243万里。[11]更重要的是，《周髀算经》建立了一套测算结合的数理模型方法，并用此模型来解释昼夜、四季及寒暑成因等问题。

除《浑仪注》外，张衡还撰有《灵宪》。西汉扬雄撰《太玄》，其“玄首序”有“驯乎玄，浑行无穷正象天。阴阳毗参，以一阳乘一统，万物资形。方州部家，三位疏成。曰陈其九九，以为数生。赞上群纲，乃综乎名。八十一首，岁事咸贞。”[12]该书点校者研究认为，张衡受到《太玄》的影响。张衡在其《灵宪》中说：“在天成象，在地成形。天有九位，地有九域；天有三辰，地有三形。有象可效，有形可度。情性万殊，旁通感薄，自然相生，莫之能纪。于是人之精者作圣，实始纪纲而经纬之”[13]，天地有形有象可以度量。这本书给出了天地的直径数据，相关论述共有两处：

(1)八极地维，径二亿三万二千三百里，南北则短减千里，东西则广增千里。自地至天，半于八极；(2)将覆其数，用重差钩股，悬天之景，薄地之仪，皆移千里而差一寸得之。[13]

据《礼记·内则疏》记载，“依如算法，亿之数有大小二法。其小数以十为等，十万为亿，十亿为兆也。其大数以万为等，数万至万，是万万为亿”[14]，张衡在《灵宪》中用的就是“小数”法，所以天和地的直径在南北方向上为231 300里，东西方向上为233 300里。从第(2)条论述可以看出张衡的相关测量利用了重差法和“日影千里差一寸”这一古制。但由于缺少算法模型，这成为了张衡浑天说的重要缺陷。

2 “天高数”与“周天里数”的数理计算

天地尺度对应两个数据“天高数”和“周天里数”，前者对应天球半径，后者对应天球赤道的周长。浑天家们需要找到这个界限，如果这两个数据不确定，天地的大小就不能确定，浑天说数理模型就无法建立起来。

除张衡外，陆绩、王蕃、祖暅等有关浑天著述以及《尚书考灵曜》、《洛书轨曜度》、《春秋考异邮》等纬书中也都记录了“天高数”与“周天里数”，依据它们“周天里数”不同及得到“周天里数”的方法也不同，现将这些数据分为三组，列表如下(表1)：

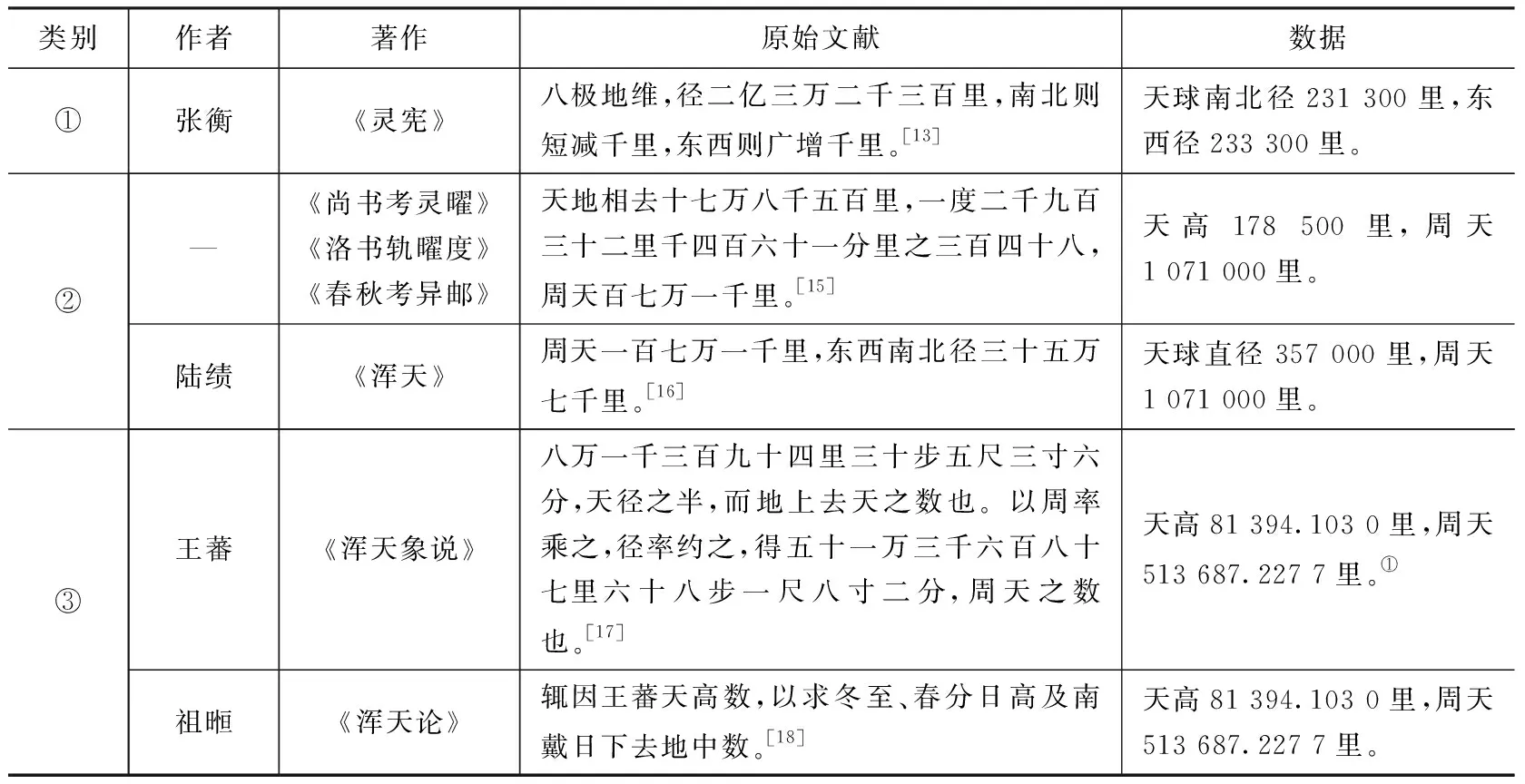
表1 张衡到祖暅时期的“天高数”与“周天里数”表 (3)当时没有现代小数表示法。为直观表示，该处及后文一些数据用现代数值表示。

三组数据存在很大的差异。从史料看，张衡、陆绩等只给出“天高数”和“周天里数”两个数据，没有清楚地说明它们的由来和本质。而纬书中的数据，查看《尚书考灵曜》原文，其中亦有“日影于地，千里而差一寸”([15]，357页)一句，似乎说明该书中的数据也是依据此古制而来。

两汉时期，以阴阳五行、天人感应学说为基础的谶纬之学盛极一时，对当时的政治、社会、学术等都产生了极大的影响。王蕃在其《浑天象说》一书中就讲述了纬书中的“周天里数”等数值对后世学者的影响程度，他说：“《洛书轨曜度》、《春秋考异邮》皆云周天一百七万一千里，至以日景验之，违错甚多。然其流行布于众书。通儒达士未之考正，是以不敢背损旧术，独摅所见”([17]，176页)，这里的“通儒达士”就包括陆绩，说明陆绩数值极有可能照搬于纬书。王蕃的另一段评述就更为直接：“又陆绩云，周天一百七万一千里，东西南北径三十五万七千里，立径亦然。此盖黄赤道之径数也。浑天盖天黄赤道周天度同，故绩取以言耳”([17]，176页)，这里进一步说明陆绩所取“天高数”和“周天里数”最早出自盖天说。在《周髀算经》中确实可以找到这两个数据及其含义([11]，35页)，它们分别对应了盖天宇宙模型中的春秋分日道径357 000里和周长1 071 000里。

学术界历来对《尚书考灵曜》等纬书主张浑天说([2]，178页)还是盖天说[19]存在争议，近来也有学者指出《尚书考灵曜》中存在的是不同于浑天说、盖天说、宣夜说的汉代第四种宇宙学说[20]。这种情况足以说明《尚书考灵曜》等纬书中宇宙学说的混乱，它们极有可能同时参考了盖天说和浑天说的内容，所以我们才会看到纬书中“天高数”和“周天里数”与《周髀算经》的一致。

陆绩继承了张衡浑天说，虽然批评盖天说“其为虚伪，较然可知”，但是在其《浑天》中兼述盖天说，而在文末最后两句直接采用了《周髀算经》的春秋分日道径和周长数值，当作浑天说模型的“天高数”和“周天里数”。这在一定程度上表明陆绩对这两个数据束手无策，鉴于这两个数据对浑天说模型十分重要，只好用他认为比较可靠的数据来收场。

张衡、陆绩等浑天家迟迟找不到合理方法来推算“天高数”和“周天里数”，这个局面一直到王蕃才有所好转。三国时期的王蕃是一位坚定的浑天家，写有《浑天象说》并制作了浑仪，他的工作既包括给出推翻盖天说模型数据的证据，同时也建立了浑天说“天高数”和“周天里数”的数理模型。

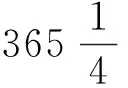
王蕃的第二个步骤是“以晷影考周天里数”[17]。按照《周礼》记载，“日至之景，尺有五寸，谓之地中”[21]，郑司农认为颍川阳城是地中所在地[21]。王蕃在其《浑天象说》中把阳城为地中的说法明确引入浑天说中。因此，《隋书·天文志上》“地中”有“《周礼·大司徒职》：‘以土圭之法，测土深，正日景，以求地中。’此则浑天之正说，立仪象之大本”[22]。《周礼》郑玄注：“凡日景于地千里而差一寸，景尺有五寸者，南戴日下万五千里也”[21]，阳城处夏至日影为1尺5寸，根据“日影千里差一寸”，太阳南戴日下与阳城的距离就是15 000里。“日影千里差一寸”这一古制是以太阳高度固定不变和大地是一平面的假设为前提，从王蕃下面的具体术文“六官之职，周公所制，勾股之术，目前定数。晷景之度，事有明验，以求推之，近为详矣”([17]，177- 178页)中可以看出他认同这一古制，这是先人直至汉代以来的重要经验，据此而得的夏至日影和南戴日下去地中距离也是确定的。基于此，王蕃完成了浑天说“天高数”和“周天里数”的数理构建。他给出了一套精密的测量“天高数”和“周天里数”的方法，他在《浑天象说》中说：

诚以八尺之表而有尺五寸景，是立八十而旁十五也。南万五千里而当日下，则日当去其下地八万里矣。从日邪射阳城，则天径之半也。以勾股法言之，旁万五千里则勾也，立八万里则股也，从日邪射阳城则弦也。以勾股求弦法入之，得八万一千三百九十四里三十步五尺三寸六分，天径之半，而地上去天之数也。倍之，得十六万二千七百八十八里六十一步四尺七寸二分，天径之数也。以周率乘之，径率约之，得五十一万三千六百八十七里六十八步一尺八寸二分，周天之数也。[17]

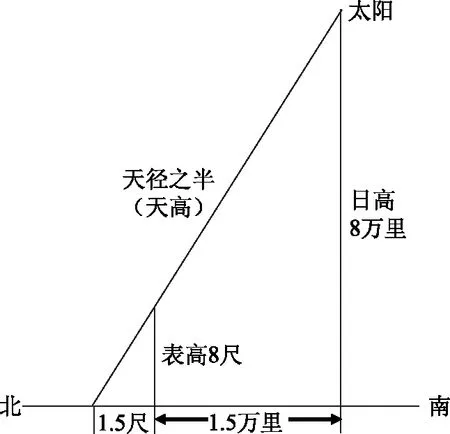
图1 夏至表影长与夏至日高关系图

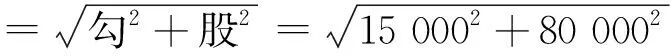
天径之数=2×天径之半=162 788里61步4尺7寸2分=162 788.206 0里；

王蕃首先根据相似勾股形对应边成比例和“日影千里差一寸”得出夏至日高数，再根据勾股术求得夏至“天高数”和天球直径，进而根据《乾象历》圆周率得到“周天里数”。王蕃立足古代经典测量数据，利用了当时最优秀的历法《乾象历》作者刘洪对周天度数和斗分的新认识，特别是由此获得的新圆周率，非常漂亮地解决了夏至“天高数”和“周天里数”问题，在尝试构建浑天说数理模型上迈出了第一步。王蕃这套方法也被南朝的祖暅所继承。

祖暅《浑天论》批评《尚书考灵曜》中“天高数”是“既不显求之术，而虚设其数，盖夸诞之辞，非圣人之旨也”[18]。王蕃的做法符合祖暅数理模型构建的期望，并且及时纠正了前人的错误。所以，祖暅直接沿用了王蕃测得的“天高数”。此外，在《浑天论》中，他利用晷影测量进一步计算了冬至、春秋分的日高数和南戴日下去地中数：

法，令表高八尺与冬至景长一丈三尺各自乘，并而开方除之为法，天高乘表高为实，实如法得四万二千六百五十八里有奇，即冬至日高也。以天高乘冬至景长为实，实如法得六万九千三百二十里有奇，即冬至南戴日下去地中数也。求春秋分数法，令表高及春秋分影长五尺三寸九分各自乘，并而开方除之为法。因冬至日高实，而以法除之，得六万七千五百二里有奇，即春秋分日高也。以天高乘春秋分影长实，实如法而一，得四万五千四百七十九里有奇，即春秋分南戴日下去地中数也。[18]

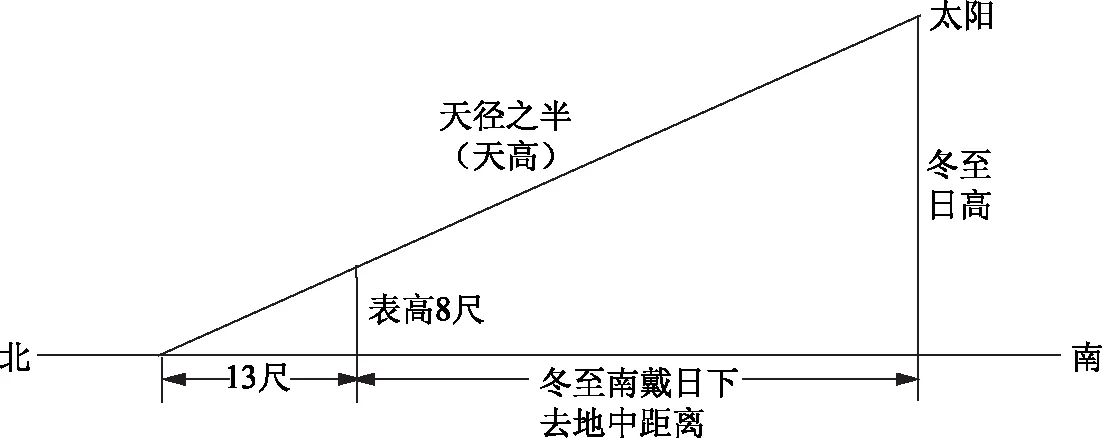
图2 日高数和南戴日下去地中数关系图

汉魏至唐初，里、步、尺的换算关系为：1里=300步，1步=6尺。[23]以冬至法为例，天高81 394.103 0里=146 509 385.364 9尺，表高8尺，冬至影长13尺，

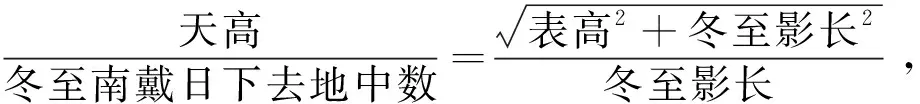
祖暅延续王蕃的工作，进一步完善了浑天数理模型。如果把王蕃夏至“日高数”和“天高数”视为浑天说数理模型的特例，那么祖暅依据浑天家的传统观念——日行黄道——即太阳附着在天壳上，直接将夏至“天高数”视为模型的定值。祖暅模型与《周髀算经》中的盖天说模型相比，用一个“天高数”和“周天里数”解释了二分二至共同拥有这个模型数据的合理性。相关数据见表2。

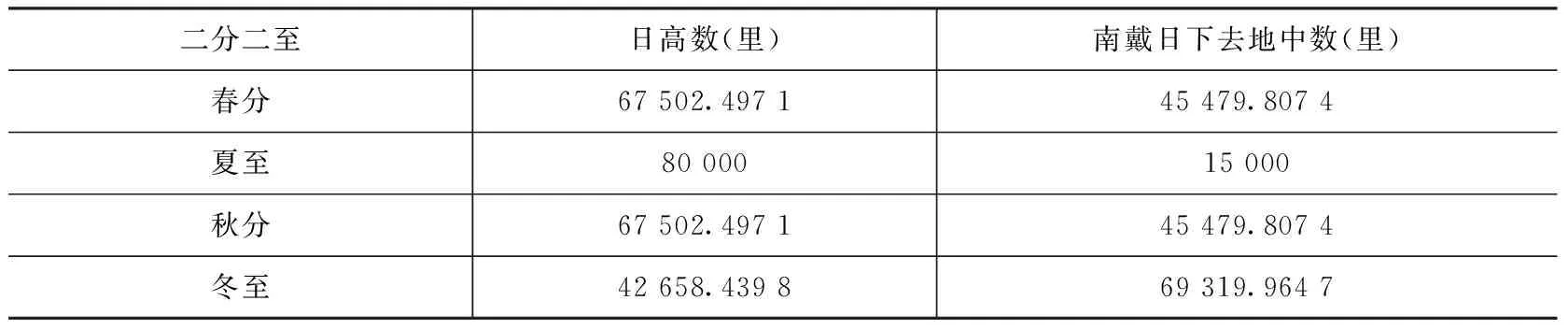
表2 祖暅浑天说模型中的日高数和南戴日下去地中数

3 汉魏南北朝浑天说数理模型的主要内容

从上文看出，张衡初步构建了浑天说数理模型，并提出计算浑天说天地边界的思想，他没有给出推算“天高数”和“周天里数”的合理方法。通过400多年的努力，陆绩、王蕃、祖暅等浑天家在浑天说假设的范围内不断改进、优化这两个数据，使得它们的数理基础有章法可循。我们将汉魏南北朝之际浑天说数理模型的特征总结为以下几点：

第一，关于天地的形状，在张衡浑天说中，天为圆球，地在天中，是一个圆形平面。后世诸如蔡邕、陆绩、王蕃、祖暅等均认可张衡的圆球状天球，其中祖暅强调“日去地中，冬夏春秋晨昏昼夜，皆同度也”[18]，更是具有高度代表性和概括性。太阳与地中阳城的距离在任意时刻都相同，即浑天上任一点到地中的距离均相等。

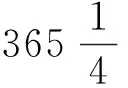
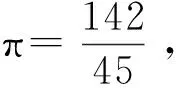
到祖暅为止，天高数和周天里数分别为81 394.103 0里、513 687.227 7里。

第四，北极和南极为天球的端点，天球绕南北极轴旋转。基于古四分历，地中阳城的北极出地高度为36度，南极入地高度也为36度。但是古代很长时间这个值是不变的([2]，146页)，对浑天家而言，如果不能正确地解释北极高的变化，则模型的构建是失败的。祖暅在《浑天论》中给出推算“北极高数”和“北极下去地中数”的方法，“推北极里数法，夜于地中表南，傅地遥望北辰细星之末，令与端参合，以人目去表数及表高各自乘，并而开方除之为法。天高乘表高数为实，实如法而一，即北极细星高地数也。天高乘人目去表为实，实如法，即去北辰极下之数也”[18]。仿照图2的方法，具体计算公式如下：

祖暅做了北极高的实际测量，通过“傅地遥望北辰细星之末，令与端参合”的方法确定人目去表数。其中，由于“人目去表数”与具体观测地点有关，不是一个确值，因此这个公式可以用在任何地点测量当地的北极高度，具有一般性。

4 从祖暅的天文实践看他对浑天说数理模型的进一步构建

祖暅在《浑天论》开篇有，“仰观辰极，傍瞩四维；睹日月之升降，察五星之见伏；校之以仪象，覆之以晷漏；则浑天之理，信而有征”[18]，这表达了他对浑天说数理模型的信念。祖暅对浑天说数理模型“信而有征”的贡献不止于完成冬至、春秋分日高以及南戴日下去地中距离的补充计算，他还讨论了日月直径关系、四季寒暑成因、地中位置的测定等内容，这些可以看作是他对浑天说数理模型的进一步论证。

4.1 测算日月直径关系

关于日月直径的大小，《周髀算经》采用相似勾股形的比例关系求得日月直径为1 250里。([11]，28页) 祖暅不同意此观点，他认为，“盖天乖谬，已详前识，无足采焉。以浑象言之，失于过大矣”([18]，184页)。

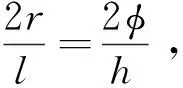
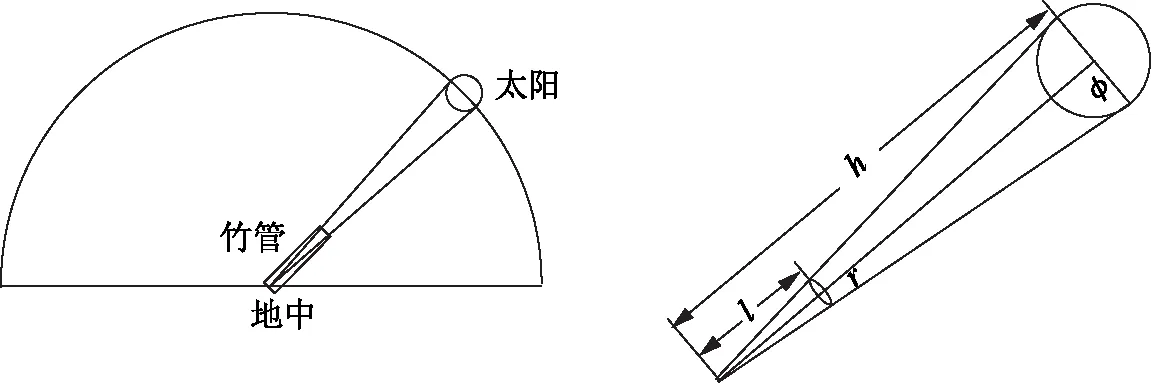
图3 日月直径与天高数关系图

祖暅的日月直径大小计算依赖于天高数和管长，而且管长可以按照具体观测情况截取一定的长度，截取一定长度的目的是使得太阳视圆面充满管口，那就是说如果管长固定，不是总能获得这个效果？这个问题与实际操作有关，也与大气折射现象有关。按照祖暅的公式，在地中的任何时间都可以直接测量太阳的视直径。遗憾的是，祖暅没有给出日月直径的具体数值。以上事实说明祖暅进行了实地观测。

4.2 解释四季寒暑成因

根据《汉书·天文志》的记载，“日，阳也。阳用事则日进而北，昼进而长，阳胜，故为温暑；阴用事则日退而南，昼退而短，阴胜，故为凉寒也。故日进为暑，退为寒”[31]，中国古代的浑天说接受了这种说法[32]，认为四季寒暑可以归因于阴阳气的自行进退、消长。

祖暅作为浑天家，没有停留于接受传统的阴阳之气进退消长之说，而是提出了另外一种解释，他说：

日去赤道表里二十四度，远寒近暑而中和。二分之日去天顶三十六度，日去地中，冬夏春秋晨昏昼夜，皆同度也。而有寒暑者，地气上腾，天气下降，故远日下而寒，近日下而暑，非有远近也。犹火居上，虽远而炎；在旁，虽近而微。[18]

按照祖暅的说法，太阳在天球上运动，无论春夏秋冬，太阳距地中阳城的距离都是一样的。之所以会有寒暑之分，是因为地气上升或天气下降而引起的，而地气或天气的运转则与南戴日下到地中阳城的距离有关。地中与南戴日下的距离近，天气就炎热；距离远，天气就寒冷。祖暅做了一个很形象的比喻，用“火居上”或“在旁”来表示太阳位置，这样，导致四季寒暑直接原因是日高的大小，日在上，日高数大，天气炎热，反之寒冷。

祖暅的解释最终归因于日高大小决定四季寒暑。而现代天文学认为，太阳高度的变化影响了地球上同一地点得到的日照能量，从而形成了春夏秋冬四季。也就是说，太阳直射点位置和太阳与地球的相互关系在不断变化，而这种观点可以与祖暅的解释相对应。如图4所示，日高数相当于太阳与地球上直射点处的距离；南戴日下到地中阳城的距离相当于地球上直射点处与地中阳城的距离，所以祖暅说“居上，虽远而炎”、“在旁，虽近而微”。如此，祖暅的解释具有一定的道理。虽然祖暅的“地平”观点与现代意义上的“地球”观念不同，但他将四季寒暑的成因与日高和南戴日下去地中距离联系在一起，也体现了他的独特见解。

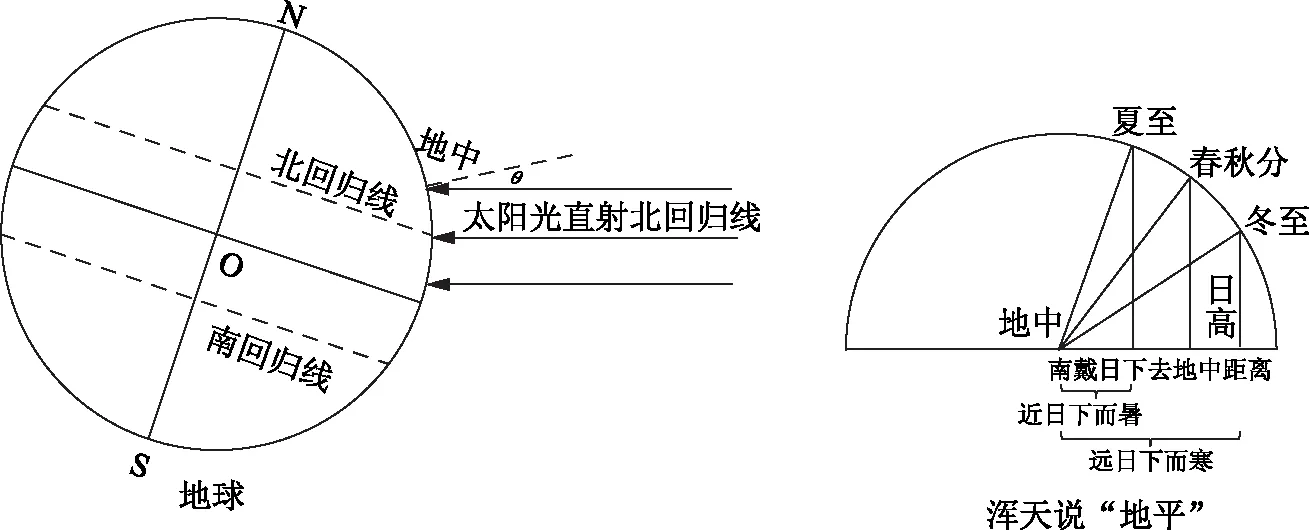
图4 四季寒暑的现代天文学解释与祖暅日高和南戴日下去地中距离图

我们不妨回顾一下《周髀算经》盖天说的观点，它认为，“日远近为冬夏，非阴阳之气”([11]，56页)，即四季寒暑取决于太阳的远近距离。可见，祖暅没有囿于盖天说的太阳远近导致四季寒暑的观点，而是把四季寒暑和“天高数”对应起来。

4.3 尝试建立测量地中的方法

前文我们已经说明，“天高数”是浑天说数理模型中至关重要的一个数据，它代表的是地中到天球的距离，而这个数据是以精确的地中位置为基础的。依照古人的认识，地中是进行天文测量的理想地点，只有在地中进行的测量才最具权威性，数据才最可靠。[33]祖暅亦是如此，他在《浑天论》中进行的观测、数据推算，都是以“立于地中”为根本。中国古代的浑天家认为阳城是大地的中心，王蕃就曾提到“天体圆如弹丸，地处天之半，而阳城为中”[17]。但阳城所代表的只是一个范围，它的几何中心，即真正的地中在哪里？历史上，祖暅的一项重要工作就是找到这个几何中心的精确位置。

《隋书·天文志》中记载有祖暅推地中所用的“五表法”：

其法曰：先验昏旦，定刻漏，分辰次。乃立仪表于准平之地，名曰南表。漏刻上水，居日之中，更立一表于南表影末，名曰中表。夜依中表，以望北极枢，而立北表，令参相直。三表皆以悬准定，乃观。三表直者，其立表之地，即当子午之正。……进退南北，求三表直正东西者，则其地处中，居卯酉之正也。([22]，522- 523页)

他通过漏刻与圭表的配合使用，来确定日中时刻日影与夜半北极方位对应的南表、中表、北表处于同一直线上，以定出地的“东西之中”；确定春秋分太阳的出没方位对应的东表、中表、西表位置，以定出地的“南北之中”；最后再依据中表的位置来定出地中。祖暅构建了一个理想的方法，试图精确测定地中位置。

由于“地中”概念以有限的地平说为基础。按照现代理论，在地球上的任何地点都可以测得正东西和正南北方向，任何地点都是当地的地中位置，所以祖暅的方法实际上并不能测出浑天的中心——地中，他给出的只能算是“影中”的测量方法，这也正是在史书中未能找到他给出的精确地中位置的原因。

5 “日影千里差一寸”与浑天说数理模型的终结与失败

从上文可知，在浑天说数理模型的构建过程中，王蕃根据《周礼》郑玄注的说法，应用“日影千里差一寸”算得夏至“天高数”，祖暅将这一数据拓展为普适意义上的浑天说“天高数”。《周礼》郑玄注、《周髀算经》盖天说以及张衡、王蕃、祖暅等浑天家对古制“日影千里差一寸”都深信不疑。冯立昇就曾指出，这一说法是浑天说和盖天说共有的，以大地是平面为前提。[34]

我们进一步考察“日影千里差一寸”的具体含义，其一，当八尺表高固定时，如果在同一地点不同季节所测中午日影长度相差一寸，那么两次测量南戴日下的位置相距一千里；其二，如果南北两地距离一千里，那么两地同一天的中午日影长度相差一寸。([34]，35页) 既然“日影千里差一寸”是构建浑天说模型的重要依据，那它是否适用于测算浑天说中任意位置的日高数据呢？根据上述两种含义，我们作图5加以说明。

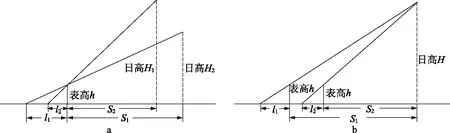
图5 “日影千里差一寸”示意图

设l1、l2分别为两次测量的影长，S1、S2分别为测量点到日下的距离，表高为h，日高为H。由于图5-a中两次观测的日高不相等，两次测量不构成直观的相似勾股形关系，那么，仅根据“日影千里差一寸”的第一种含义可得：

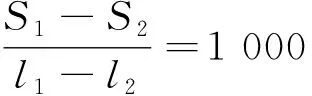
(1)

而根据图5-b所示情况，由于日高为一定值，我们可以进一步得到以下关系式：

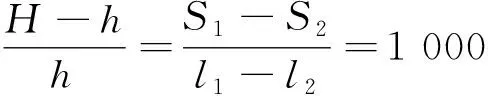
(2)

为了验证这两个关系式是否自洽于浑天说数理模型，我们将祖暅计算的二分二至日高数和南戴日下去地中数代入其中。

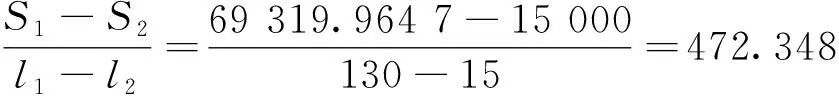
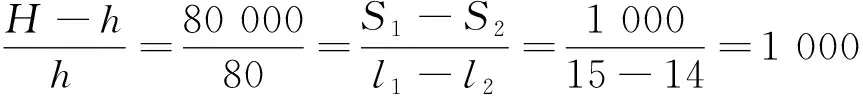
祖暅曾经实测得到二十四节气晷影长度[35]，把这些数据逐一代入上述两个关系式，最终我们发现：只有按照第二种含义在夏至日测量时，同一天南北相距1 000里处的日影差满足关系式(2)，而其他节气的观测值均不符合关系式(1)和(2)。

实际上，按照“日影千里差一寸”的第一种含义，只有当日高H与表高h的比值为定值1 000里/寸时，“日影千里差一寸”才能适用于浑天说模型中相关距离的计算。由于浑天说模型的“天”是一个球面，日高在不断变化，日高与表高的比值也在变化。除了夏至日观测的特殊情况外，“日影千里差一寸”并不适用于浑天说数理模型。而王蕃、祖暅等人均没有发现这一致命缺陷。王蕃利用夏至日影测量的特殊情况计算“天高数”，祖暅未加分析直接运用相似勾股形的比例关系，在实际构建模型时罔顾“日影千里差一寸”的使用条件。但是值得肯定的是，祖暅重视实际天文测量，具有相当的算学水平，特别是他在北极高测量、日月直径关系、四季寒暑成因等模型构建和解释方面有许多创建。

祖暅之后，一些学者对古制“日影千里差一寸”提出质疑。刘焯率先发难，“张衡、郑玄、王蕃、陆绩先儒等，皆以为景千里差一寸，言南戴日下，万五千里。表景正同，天高乃异。考之算法，必为不可。寸差千里，亦无典据。明为意断，事不可依”([22]，521-522页)，指出这一古制不能用于“天高数”和南戴日下去地中距离的计算。一行更是通过实地测量证明了“日影千里差一寸”与实际情况不符。唐开元十二年(公元724年)，一行组织了全国的天文大地测量工作，得出正南北方向上的滑州白马县到上蔡武津县的距离与影差关系为“大率五百二十六里二百七十步，影差二寸有馀”[36]，即南北相距526里270步影差2.05寸。据此，一行认为“旧说王畿千里，影差一寸，妄矣”[36]，从而推翻了“日影千里差一寸”的历史说法。

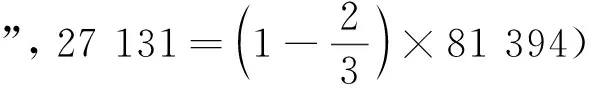
此外，浑天说持“地平”观点，浑天家没有考虑到其实地中以外的人所看到的“天高数”和“周天里数”并不相同。浑天家赓续古代的地中说，试图把它作为前提，实际上地中并不存在。这些都使得浑天说模型难以从逻辑上自洽，失败也就必然了。

王蕃推算“天高数”和“周天里数”的方法固然给浑天说数理模型提供了理论基础，但“日影千里差一寸”之说与浑天说模型并不相容，一行将“日影千里差一寸”和王蕃的数据推翻后，后世的浑天家们再没有找到新的方法测算准确的“天高数”，浑天说数理模型的构建也就以失败告终。

6 结 语

本文在史料基础上重点考证了汉魏以来400年间浑天说数理模型的建立过程。张衡首先从数理上对浑天说进行了论述，他受西汉扬雄《太玄》的影响尝试推算浑天说的天地尺度，他只给出了天地直径的数据，而缺少相应的测算依据。在张衡之后，陆绩、王蕃、祖暅等浑天家先后加入到天地尺度的讨论中，王蕃首次基于一定的测算原理给出“天高数”和“周天里数”。他的数理探索加进古代历法的最新成果，把浑天说与历算结合起来。祖暅认同王蕃的数据和方法，同时补充了冬至、春秋分的相关数据和北极高度测算过程等。

祖暅应用他的浑天说模型解释和论证了日月直径关系、四季寒暑成因、测地中之法等的原理，其中不乏他的个人实践与创造和模型严谨化的趋势，这也验证了他对浑天说数理模型“信而有征”的说法。通过本文的讨论，有助于学术界对浑天说数理模型建立新的认知。

本文最后从数学模型的角度分析了“日影千里差一寸”的适用条件，天地平行、日高固定是它的理想条件。由于浑天说模型的“天”是一个球面，日高在不断变化，日高与表高的比值也在变化。除了夏至日观测的特殊情况外，王蕃和祖暅并没有意识到“日影千里差一寸”在浑天说模型中根本不能成立，也没有发现这一致命缺陷，所以他们构建的数理模型以失败告终。古制“日影千里差一寸”作为浑天说的一条重要依据，到一行时被彻底推翻。

如文中所述，中国古代浑天说数理模型虽然只有少数浑天家参与建构，但是历史上参与或至少关注此事的不乏一些数理天文学家，如张衡、刘洪、王蕃、何承天、祖冲之、祖暅、刘焯、一行等人，他们都有优秀的历法问世，其中张衡也曾经与周兴共同完成了《九道法》。历法推步不可避免地涉及周天度数、去极度、圆周率、日影测量、日月直径、北极出地等概念，以上概念和理论也是浑天说数理模型必须面对和解决的。由此可见传统数理天文学与古代浑天说非同寻常的关系。应该说，浑天说在用数理解释周天度数、去极度、北极出地等方面比盖天说具有明显的优势，特别是它的圆周率一直跟进古代历算家的最新成果，采用渐进分数，这一点比《周髀算经》的“周三径一”要好很多。

致 谢感谢本文审稿专家提出的宝贵意见与建议。感谢本刊主编邹大海先生耐心细致的修改建议!