基于遗传算法的甘肃省应急物流配送路径优化研究*
马丽荣,尹耀杰
(兰州石化职业技术大学国际商务学院,甘肃 兰州 730060)
近年来,甘肃遭受了多种自然灾害,如地震、滑坡、山体崩塌、雪灾、风雹、低温冷冻、洪涝、干旱、泥石流等,特别是低温冷冻、洪涝、风雹灾害最为频繁,也最为严重,各种自然灾害给全省群众生活及农牧业生产造成严重的影响。2020 年,自然灾害共造成全省485.47 万人次受灾;因灾遇难32 人、失踪3 人;紧急转移安置9.06 万人;房屋倒塌3131户、1.16 万间,严重损坏9838户、4.71 万间,一般损坏2.92 万户、15.55 万间;农作物受灾396.33 千hm2,其中成灾250.65 千hm2,绝收33.41 千hm2。直接经济损失约337.32 亿元[1]。自然灾害发生以后,提高政府部门对突发事件调控和应对能力,保证应急物资供应和市场价格基本稳定带来了巨大的挑战,应急救援物资需要在有效的时间内输送到灾区,应急物资的快速供应直接关系到救援的成效。那么,灾后应急物资如何及时有效的供应,应急物流设施如何定位,应急物流配送路径如何规划等等问题,是应急救灾工作急需研究的课题。应急物流是应急管理系统的重要组成部分,主要承担应急物资的储备、运输、配送及回收废弃物的职责。
如何以最短路径、高满意度、最低成本等为目标在最短的时间内完成突发事件下应急物资的配送,已成为国内外学者高度关注的问题。李志等[2]研究了以物资分配公平性和需求效用最大化为目标,建立基于多目标的混合整数规划方法应急物资供应点定位-分配模型;杨恩缘等[3]提出了以运输成本最小为目标,结合容量限制及应急配送的多样性和多级性特点,构建了应急物资多级配送选址-路径的混合整数规划模型;陈湉等[4]提出基于离散蜂群的灾害应急物流车辆调度优化问题研究,以供应过量、物资分配不足所造成的损失最小化、车辆调度成本最低为优化目标,以服务时间窗和车辆运载能力为约束条件,构建了应急需求下的车辆调度优化模型,并采用离散蜂群算法求解;张伟等[5]以运输距离最短化、运输时间最小化和路径复杂性为目标,建立多目标应急物流路径规划模型;蒋杰辉[6]利用改进智能水滴算法求解应急物资配送中车辆路径优化问题;朱娜[7]采用“矢量投影-理想点法”以车辆运载能力等为限制条件,以应急运输成本、应急时间及救灾点数量为优化目标构建了应急物资分配模型;朱佳翔[8]等以运输时间最少、成本最优以及用户满意度最大等为目标,构建多阶段多目标应急物流配送的灰色动态规划模型。
1 问题的描述
车辆运输路径问题(VRPTW)是应急物流研究的基本问题,也是实现在有限时间内实现物资的及时送达,提高救援效率,将灾害降到最小化的有效途径。文章针对甘肃应急物流运输与配送问题,构建了以车辆数最少和路径最短为目标的车辆配送模型,设计遗传算法对应急物流配送路径模型求解,兼顾考虑多个制约条件,如车辆载重量的限制,受灾点对物资需求时间窗的限制等。假设有多个配送中心对多个受灾点进行应急物资配送,配送中心有容量不同的车辆,受灾点对物资需求的时间各不相同,要求在规定的时间内完成配送任务,规划配送路线并要求每条路线上只有一辆车配送,规定车辆从配送中心出发完成配送任务后再返回配送中心,利用MATLAB 软件编程求解,求出应急物流低成本高效率的配送路径最优解。
2 构建应急物流配送路径模型
2.1 模型参数与变量定义
N={0,1,…,n,n+1}是节点集合,0,n+1 表示配送中心,需求点编号为{1,…,n};
di:需求点i 的需求量;
K={1,2,…,k}是车辆集合;
A:弧的集合;
xijk={0,1},表示车辆k 是否从i 点出发前往j点,如果车辆k 是从i 点出发前往j 点,则xijk=1,否则xijk=0;
Cij:表示i 点和j 点之间的距离;
wik:表示车辆k 对i 点的开始服务时间;
si:表示受灾点i 的服务时间;
tij:表示从i 点到j 点的行驶时间;
Mij:一个足够大的数,可以取10 的7 次方;
ai:受灾点i 的左时间窗;
bi:受灾点i 的右时间窗;
E:配送中心的左时间窗;
L:配送中心的右时间窗;
Ck:车辆k 最大装载量;
s+(i):表示从i 点出发的弧的集合;
s-(j):表示回到j 点的弧的集合。
2.2 模型设计[9]


其中目标函数(1)表示车辆使用数目最少和车辆行驶总距离最短,将这两个目标合为一个目标表示配送成本最低;(2)~(10)是约束条件,(2)表示每个需求点只能被分配到一条配送路径上;(3)表示每条配送线路上从配送中心出发只能前往一个需求点;(4)表示车辆k 在路径上的流量限制;(5)表示车辆配送完毕都必须返回配送中心;(6)表示配送时间连续性;(7)表示需求点时间窗约束;(8)表示配送中心时间窗约束;(9)表示载重量约束;(10)表示变量取值的约束。
3 基于遗传算法(GA)的应急物流配送路径模型求解
3.1 算法设计
3.1.1 编码
在使用GA 求解VRPTW 问题时,可以采用整数编码的形式对染色体进行编码,当配送车辆数最多为K,且节点数目为N 时,染色体长度为N+K-1,那么表达该染色体的基本形式为(1,2,3,…,N,N+1,…,N+K-1)。
3.1.2 遗传适应度函数
当编码的解码不能保证都满足每条配送路线上对时间窗的约束和载重量的约束条件时,为了解决违反约束问题,那进行求解时采用惩罚函数。构建的惩罚函数如下:f(s)=c(s)+αq(s)+βw(s),c(s)表示车辆总行驶距离,q(s)表示各条路径违反的容量约束之和,w(s)表示所有顾客违反的时间窗约束之和。因为,违反容量约束相对来说不太容易,所以,将α 设为10,而较容易违反时间窗约束,所以,将β 设为100。
目标函数值越小越优越,因此,在选择环节,将惩罚函数的倒数设置为适应度函数,即为1/f(s)。
3.1.3 初始化种群
先构建带时间窗车辆路径问题的初始解,再进行初始化种群。
设节点数目为m。
第一步:任意选择某一节点i∈{1,2,3,…,m};
第二步:使用车辆数的初始化k=1;
第三步:遍历节点生成序列Sq=[i,i+1,…,m,1,2,…,i-1]
第四步:遍历节点j 至节点m,形成初始解。按序列Sq 遍历节点Sq(j),将节点Sq(j)添加到第q 条路径中,在添加到对应线路中时要考虑车辆的载重量和左时间窗的约束条件。
得到的初始解就是一个配送方案,通过将个体赋值的方式转换为种群初始化。
3.1.4 选择
从群体中选择优良个体来繁殖子代的过程,并进行优胜劣汰操作,通过基于适应度的过程选择个体解决方案,即从群体中选择多个适应度值大的个体进行交叉、变异以及局部搜索过程。
3.1.5 交叉
交叉是指新的个体由两个父代个体的部分结构加以替换重组而生成的。
3.1.6 变异变异过程是指子代染色体由父代染色体的这两个位置上的基因互换形成的。
3.1.7 终止条件
遗传算法具有随机搜索特性,需要设置终止条件,以在可接受时间内获得最优解。比如设置最大进化次数为终止条件,或达到最大迭代数时终止算法运算,再如判断种群适应度值的收敛性,种群适应度值不被继续优化时终止算法运算。
3.2 遗传算法的运算流程
遗传算法(GA)是借鉴生物界的进化论,适者生存,优胜劣汰的遗传机制演化而来,是一种随机化搜索全局寻优的生物进化过程算法,具有内在的隐并行性和更好的全局寻优能力,采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,使群体不断进化,逐渐接近最优。GA 是解决VRPTW 问题的有效方法之一,在求解应急物流配送模型中得到了广泛的应用[10],如图1所示。
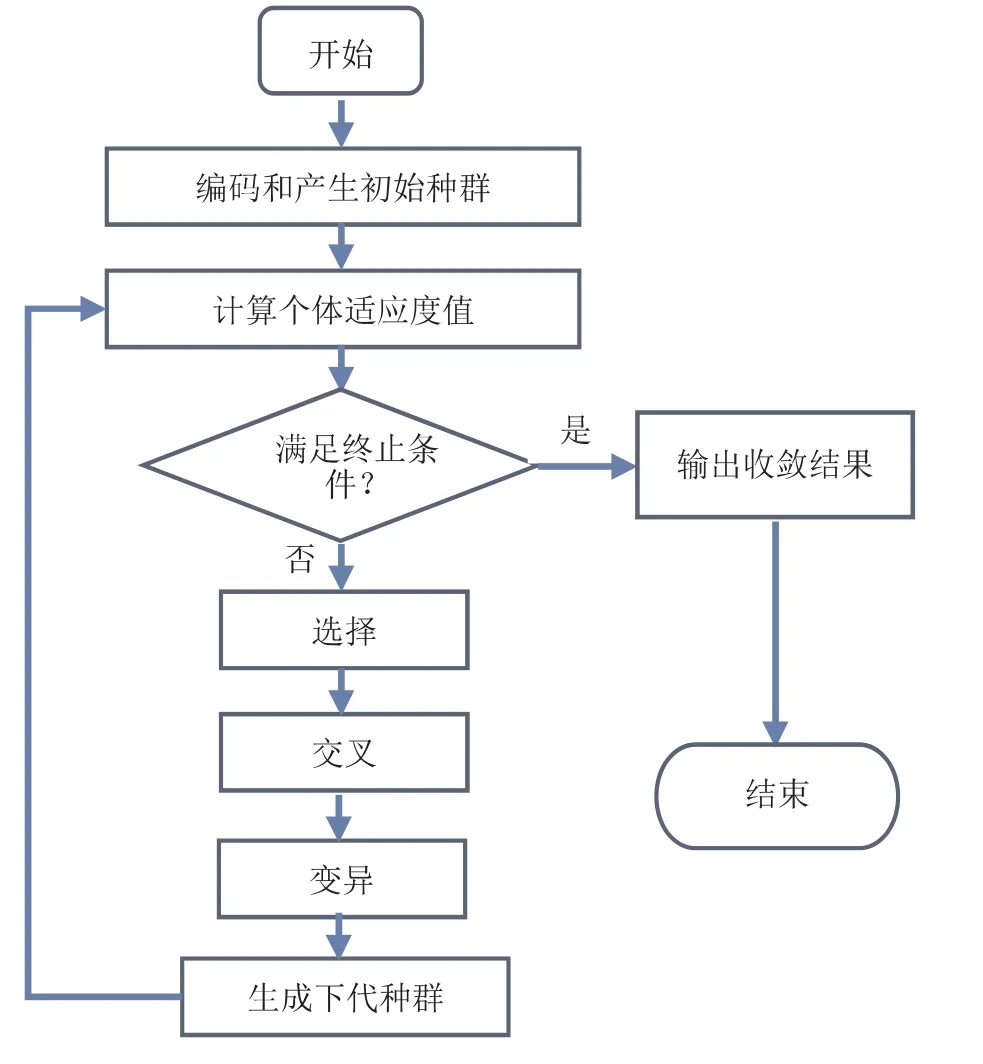
图1 遗传算法流程图
4 算例分析——以甘肃省定西漳县和岷县为例
甘肃省定西市漳县和岷县自古有“西控青海,南通巴蜀,东去三秦”之说,地处黄土梁峁地带,山峦环抱,沟壑纵横,是地震等自然灾害高发地区,自然灾害发生以后,灾区需求大量的应急物资,由于灾区地形地貌的特殊性,严重影响了对应急物资的配送,有必要在灾区附件设置临时的应急配送中心点,临时应急配送中心负责为附近的乡镇配送应急物资。本文以定西市漳县和岷县为研究对象,两县共有31 个乡镇,利用奥维互动地图查找到31 个乡镇的二维坐标经度和维度,在模型计算中受灾点的需求量是按照各乡镇人口数量、受灾程度等信息估计得到,在考虑配送距离和受灾点需求量的情况下构建应急物流选址模型,利用免疫算法优化求解,采用MATLAB 软件对设计进行编程实现,见表1。
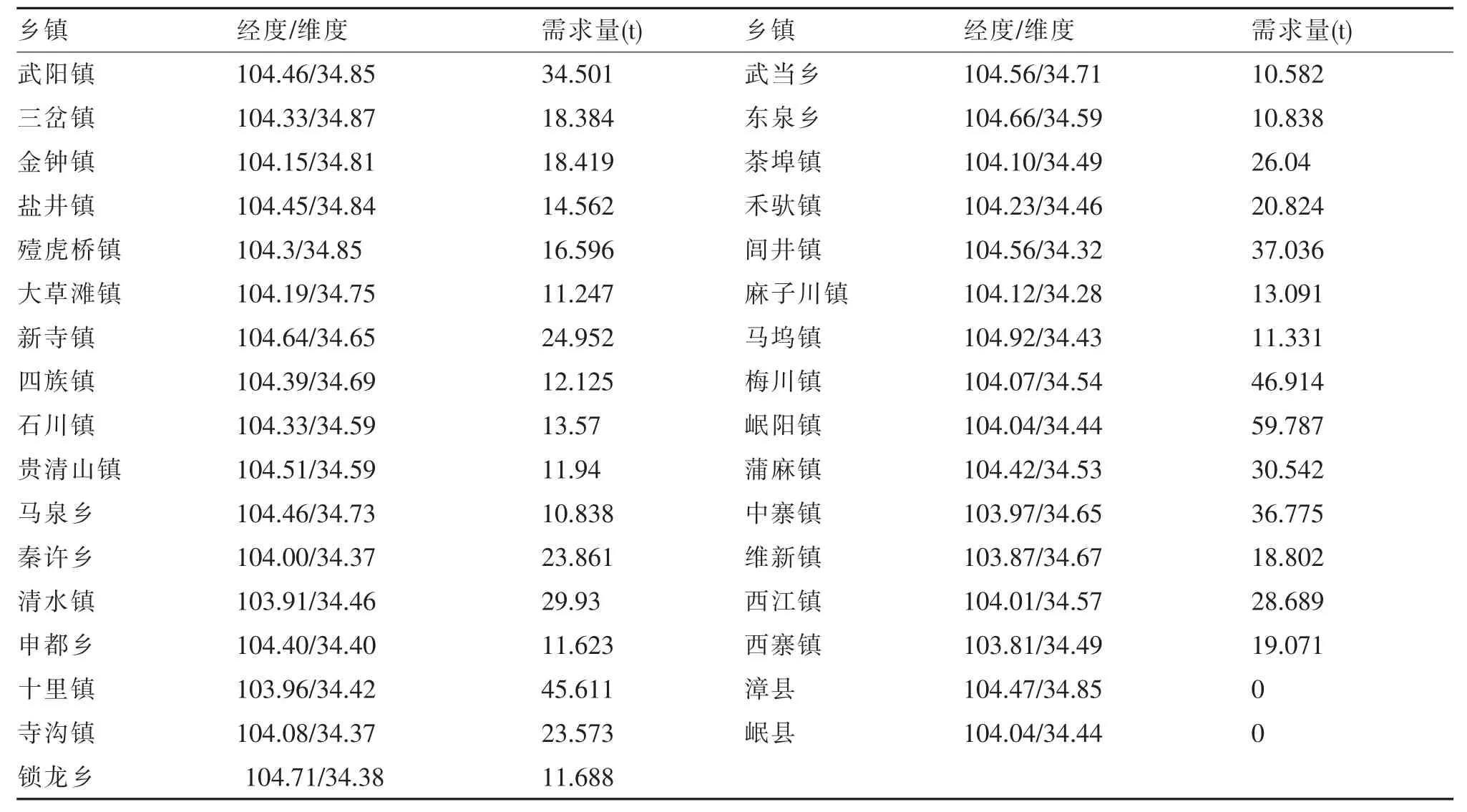
表1 甘肃省漳县和岷县各乡镇的数据资料
案例中,采用免疫算法确定了5 个乡镇为配送中心点,结果如图2 所示。以这5 个配送中心点为出发点完成邻近乡镇的配送路线规划,采用MATLAB 软件对设计的GA 算法进行编程实现,程序运行时间短,计算效率较高,有效实现了在规定的时间内应急物流配送路径规划。软件求解结果如图3 所示,最优配送路径见表2。
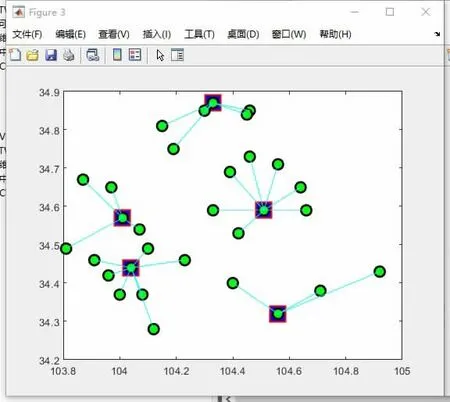
图2 应急物流中心图

图3 配送路径优化图
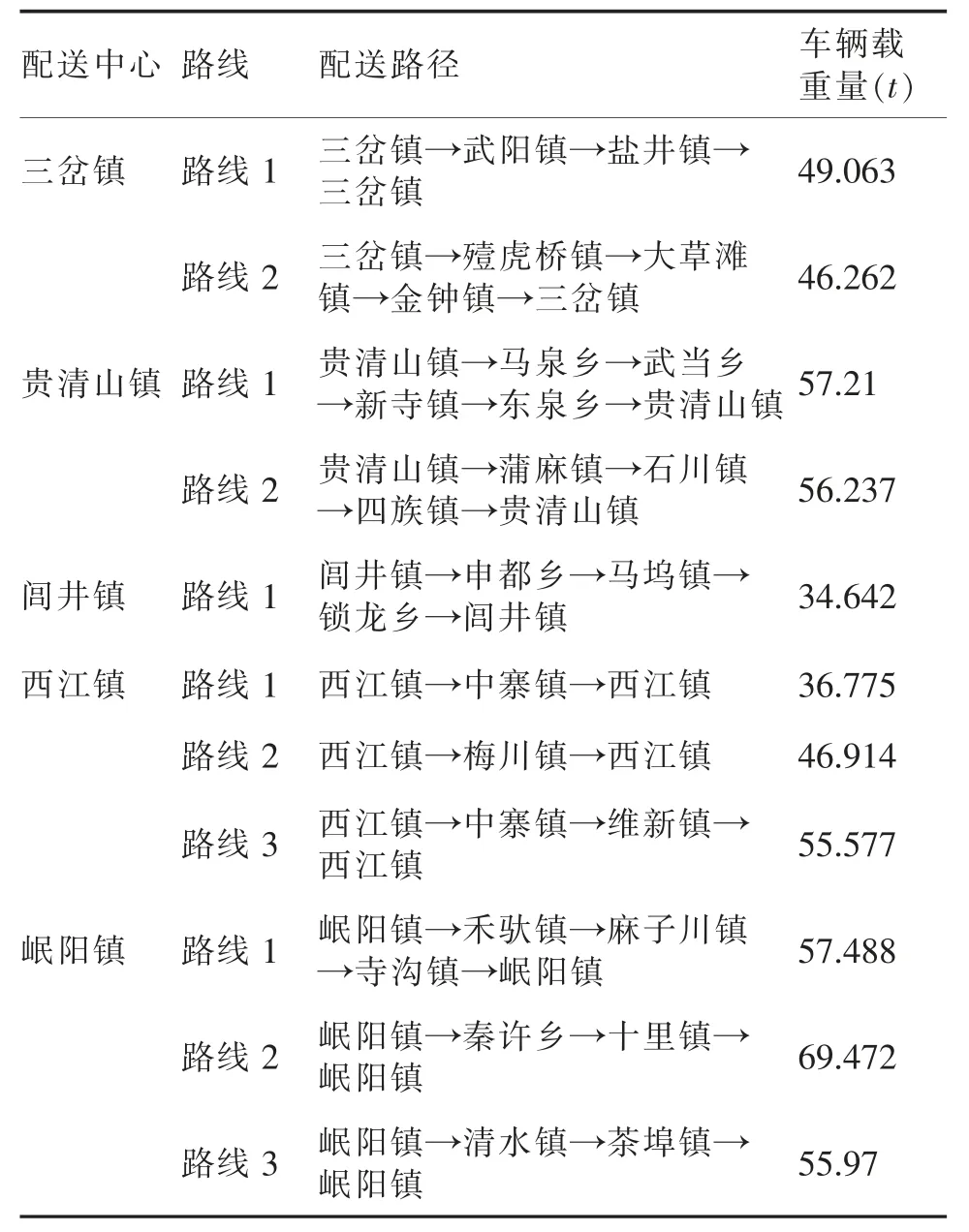
表2 多配送中心的配送路径优化结果
5 结语
文章针对配送中心如何向灾区配送应急物资这一问题,提出了基于遗传算法的应急物流车辆配送路径优化方案,构建了以车辆数最少和配送路径最短为目标,综合目标是以应急物流成本最低为目标,满足多个约束条件下优化问题模型,结合模型特点使用遗传算法进行求解。研究结果表明,遗传算法能有效的解决应急物流配送路径问题,大大缩短应急配送时间,节约成本,提升满意度,提高配送效率。

