液滴碰撞Janus 颗粒球表面的行为特征*
彭家略 郭浩 尤天涯 纪献兵 徐进良
(华北电力大学低品位能源多相流与传热北京市重点实验室, 北京 102206)
为研究液滴碰撞Janus 颗粒(双亲性)球表面的独特行为特征, 以粒径为5.0 mm 铜球为材料制备了Janus颗粒, 用直径为2.0 mm 的液滴, 在韦伯数(We)为2.7, 10, 20, 30 的测试情况下对Janus 颗粒球表面进行了碰撞实验.结果表明: 液滴碰撞Janus 颗粒球表面后的运动可分为铺展、回缩、振荡和回弹4 个过程.在不同We 下, 液滴碰撞Janus 颗粒后的运动状态主要与表面润湿性相关, 在Janus 颗粒亲水侧表现为铺展特性且铺展系数γ 随着时间t 的增大而逐渐增大并趋于稳定; 但在疏水侧, 表现为回弹现象, 铺展系数γ 会出现类似“抛物线”形状; 当液滴碰撞Janus 颗粒球表面亲-疏水分界线时, 液滴铺展和回弹同时发生.基于能量平衡和受力分析发现, 液滴动能和表面能的互相转化是液滴铺展的关键, 液滴会在重力、惯性力、表面张力、黏性力、接触力等力的综合作用下展现其独特的行为特征并最终达到平衡状态.
1 引 言
液滴碰撞壁面现象广泛存在于大自然中, 与MEMS、喷涂、农药喷洒和喷雾冷却等[1−5]农业、工业过程息息相关, 因此液滴碰撞壁面的行为特征引起了研究者的极大关注.液滴碰撞后的行为受液体性质、表面几何形状、表面润湿性、液滴碰撞速度[6−10]等多种因素的综合影响, 会发生铺展、回缩、液滴分离、飞溅等行为.目前, 液滴碰撞壁面的研究主要集中在平滑的刚性表面上[11−13], 并取得很好的成果, 但由于液滴碰撞球表面的复杂性, 液滴碰撞球壁面的研究并没有取得较为系统的总结.因此通过实验、模拟和理论分析等方法对液滴碰撞球壁面行为进行研究也成为当下的热点.郑志伟等[14]采用CLSVOF (couple level-set and volume of fluid)方法建立了液滴冲击球形凹曲面的数值计算模型, 发现其先后呈现出铺展、收缩、振动及回弹等状态, 同碰撞平面过程基本一致; 并在不同雷诺数下对平面与凹曲面的液滴最大铺展系数进行了系统研究.Khurana 等[15]利用实验和理论相结合的方法对亲水性和疏水性球表面进行了液滴碰撞行为研究, 并提出了一种基于能量平衡原理的数学模型预测了球形物体的最大铺展角, 其理论值与实验结果吻合较为良好.Amirfazli 和Banitabaci[16]研究了液滴碰撞速度对于液滴动力学的影响, 并对较大参数范围 (0.1 < We < 1146)内的碰撞问题进行了研究, 且首次对球直径小于液滴直径的情况进行了实验研究, 当球与液滴直径大小比值不同时, 液滴碰撞后运动状态也会随之发生变化, 甚至出现液滴穿透球的现象.Bakshi 等[17]首次对液滴撞击球形目标进行了实验和理论研究, 通过球形表面的液膜变化将液滴碰撞过程划分为: 初始液滴变形、惯性控制和黏性主导3 个阶段, 建立了球面液膜的流动模型, 理论分析得出球面薄膜厚度的演化方程, 并且理论预测与实验结果具有良好的一致性.
虽然液滴碰撞球表面已取得一些研究成果, 但其大多数集中在单一润湿性表面, 对液滴碰撞两种润湿性表面集于1 个的球面的研究较少.近年来,由于人们对亲疏水性的认知应用的扩展, 人们对具有两种不同性质的同一粒子 (Janus 颗粒)产生了浓厚的兴趣并逐渐应用于实际.“Janus”(古罗马神话中的双面神)一词, 首次在1991 年, 由Gennes[18]在诺贝尔颁奖大会上提出并使用.后来Janus 粒子被定义成表面具有不同化学性质或物理性质的不对称粒子.本文的Janus 颗粒是指颗粒具有一半亲水, 一半疏水特性.目前国内外对液滴碰撞Janus颗粒的研究较少, 正确的认知液滴碰撞Janus 颗粒球表面的行为特征对深化Janus 颗粒的应用具有重要的价值.因此本文制备了Janus 颗粒并搭建了液滴碰撞Janus 颗粒球面的实验装置, 测试了液滴在不同韦伯数下分别碰撞Janus 颗粒球表面亲水侧、疏水侧和Janus 亲疏水分界线的行为特征, 详细分析了液滴碰撞的行为动态变化过程, 并对液滴在运动过程中的受力进行分析.
2 实验材料与方法
2.1 表面制备及表征
制备Janus 颗粒所使用的材料粒径为5.0 mm的紫铜球, 将紫铜球先后经过去离子水、丙酮、乙醇、稀盐酸和去离子水超声波清洗过程, 得到表面干净的紫铜球颗粒; 然后将其均匀放置在丝网上,对裸露在上方的半球喷涂超疏水喷雾剂 (美国超技术公司生产), 下半球不做处理, 再将其置于通风口处1.5 h 后则得到Janus 颗粒.为了进一步确定液滴在Janus 颗粒球面上的润湿性, 对液滴在球表面上的静态接触角进行了多次测量, 发现液滴在亲水侧的静态接触角为66°, 在疏水侧的静态接触角为150°.
本实验环境温度为25 ℃, 所使用的液滴为去离子水, 液滴体积为4.0 µL, 等效直径约为2.0 mm,其密度ρ 为998.2 kg/m3, 黏度µ为1.005 × 103pa·s,表面张力σ 为72.75 × 10–3N/m.
2.2 实验系统与方法
实验装置如图1 所示, 主要由玻璃注射器、高速摄影仪、微流量液滴控制器、挡风玻璃、LED 背光灯和实验样品组成.其中玻璃注射器(带有不锈钢的疏水针头)容量为5.0 ml, 针头外径为0.2 mm.微流量液滴控制器可通过调整升降台使液滴获取不同的滴落高度, 从而赋予液滴不同的碰撞速度0.3, 0.6, 0.8, 1.1 m/s, 所对应的韦伯数分别为2.7,10, 20, 30, 对应的雷诺数分别为621.8, 1191.9,1589.2, 2185.1.

图1 液滴碰撞球面实验装置系统 1.计算机; 2.高速摄影仪; 3.微流量液滴控制器; 4.Janus 球; 5.可调节底柱Fig.1.Experimental set up of the droplet collision on spherical surface.1.Computer; 2.high speed camera; 3.digitized microliter droplet dispenser; 4.Janus sphere; 5.adjustable bottom column.
实验时, 首先利用计算机精确设定液滴直径大小及玻璃注射器的推进速度, 达到预定体积后液滴会从针头处脱落, 以自由落体状态碰撞颗粒球表面, 碰撞的整个过程由高速摄影仪进行记录, 拍摄帧率为4000 Hz、像素为1016 × 1016.实验中可以通过调整升降台使液滴获得不同的滴落高度.为获得液滴碰撞球表面的瞬时速度u, 利用Photoshop的图像处理功能, 选取液滴碰撞壁面前Δt, 2Δt,3Δt, 4Δt 时间间隔的4 张图片, 测量液滴距壁面碰撞点的距离h, 再通过时间t 和距离h, 则可得出液滴碰撞表面的瞬时速度u.此外液滴在下降过程中由于空气阻力的影响会使液滴表面形态发生一些变化, 为了确保实验结果的精确性, 整个实验过程都将在封闭环境中进行.
在液滴碰撞颗粒球表面过程中, 液滴碰撞行为特征会受到工质物性、液滴直径大小等许多因素影响, 因此为了简化分析, 采用韦伯数和雷诺数对液滴碰撞壁面过程进行无量纲分析.其中韦伯数表示惯性力和表面张力的比值, 当We > 1 时, 表示在碰撞过程中液滴的动能占据主导地位.

其中, ρf为液滴密度, u 为液滴碰撞速度, σ 为液滴的表面张力系数.
雷诺数表示惯性力和黏性力的比值, 当Re > 1时表示碰撞过程中惯性力起主导作用.

其中, µ为液滴的黏性系数.
同时为了更加形象地描绘出液滴碰撞壁面后的铺展特性, 提出了液滴碰撞壁面的无量纲铺展因子γ:

其中, a 为液滴在球面的铺展半径, d 为液滴直径.
3 实验结果与讨论
3.1 液滴碰撞Janus 颗粒疏水侧的行为特征
如图2 所示为液滴碰撞Janus 颗粒疏水侧时的具体运动状态, 可发现在韦伯数介于2.7 至30 下液滴的运动过程几乎一致, 先在表面铺展然后迅速回弹, 直至液滴脱离颗粒球表面.因此可将液滴在疏水侧的运动大致划分为: 液滴铺展初期(I)、缓慢铺展 (II)、回弹 (III)及完全脱离 (IV)4 个过程.
过程I (0—0.75 ms)中, 由于液滴从一定高度滴落, 因此液滴碰撞Janus 颗粒球表面时, 会以碰撞点为中心迅速向四周铺展, 在此过程中液滴的动能逐渐向表面能和黏性扩散能[19]转化.在We =20, t = 0.75 ms 时 (如图2 所示)液滴出现分层现象, 形成“球冠状”, 造成这种现象的主要原因是:在碰撞过程中, 由于液滴本身具有的冲击动能和颗粒表面的亲疏水特性造成了液滴在表面的快速铺展; 但液滴在铺展过程中会产生毛细波[20], 毛细波向液滴的传播则阻碍了上部液滴的惯性铺展过程.
过程II (0.75—3 ms)中, 从图2 可发现液滴在表面张力和黏性力的共同作用下, 铺展变慢, 意味着速度的减小.那么这种现象的原因究竟是表面张力主导还是黏性力主导呢?为了探究这个问题,Clanet 等[21]提出了可以区分表面张力主导和黏性主导两种流动机制的参数P:
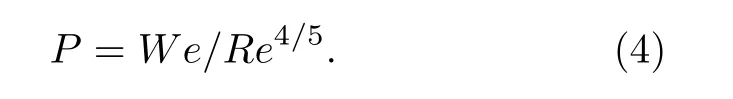
得出了在P < 0.3 时表面张力主导; 相反则是黏性力主导.经过计算临界速度为vr= 3.667 m/s, 而本实验中液滴的速度分别为v = 0.313, 0.6, 0.85,1.05 m/s, 显然均小于临界速度, 则过程II 中主要由于表面张力的作用使液滴扩散速度减小.当液滴在t = 3 ms 时, 液滴达到最大铺展长度, 此时液滴的动能为零, 表面能最大.
但过程III (3—8 ms) 中, 不论We 大小液滴都会沿球壁面方向运动 (如图2 蓝色箭头所示),在表面张力的作用下液滴发生回弹现象.过程IV(t > 8 ms)中液滴完全脱离颗粒表面.
为了更全面分析We 对铺展因子γ 的影响, 图3给出了液滴在4 种韦伯数下撞击球颗粒的情况, 曲线大致呈现出“抛物线”形状, 我们的结果与Khojasteh 等[22]文献中的具有相同性, 在液滴碰撞超疏水球面时, 不同韦伯数下铺展因子γ 随时间的变化趋势几乎相同.可看出在过程I 中液滴铺展因子γ 基本相同, 表明在液滴铺展初期We 变化对铺展因子γ 影响较小, 几乎可以忽略.过程II 中不同We下达到最大铺展长度所需要的时间基本相同, 说明We 变化对液滴铺展速率影响较小.针对这种现象Mitra 等[19]和Khurana 等[15]计算出液滴碰撞球壁面的黏性扩散能可知虽然液滴碰撞壁面动能越大, 但铺展过程中黏性扩散能也增大, 故在不同We 下液滴达到最大铺展因子时所需时间较为接近.过程III 中铺展因子γ 随时间增加呈指数下降.直到过程IV 时, 液滴完全脱离颗粒球表面, γ = 0.
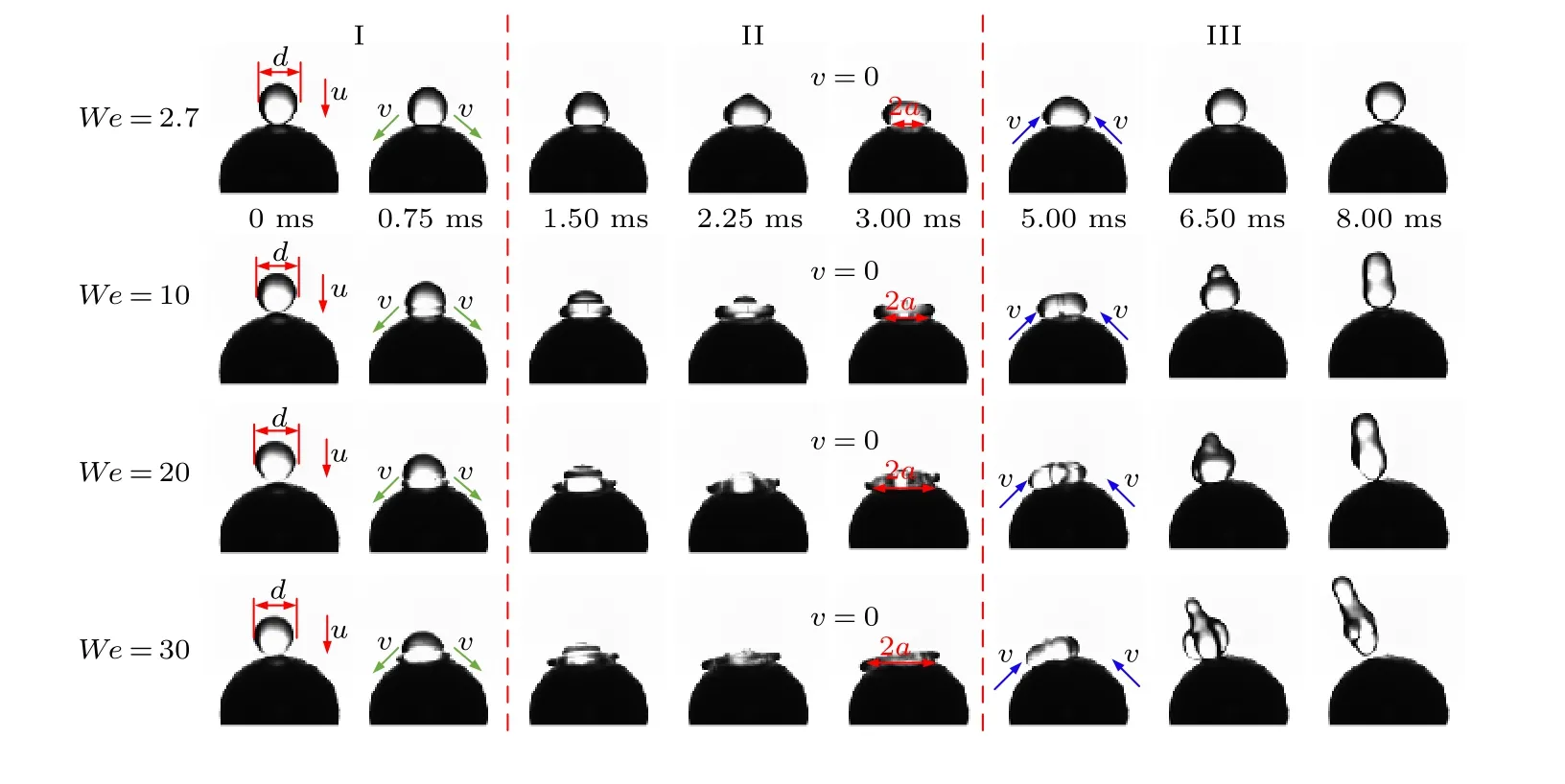
图2 不同We 下液滴碰撞疏水侧球面行为的动态过程Fig.2.Dynamic behavior of droplet collision on the hydrophobic spherical surface under different We.

图3 不同We 下的动态铺展因子变化(疏水侧)Fig.3.Dynamic spreading factor of droplet collision under different We (hydrophobic side).
3.2 液滴碰撞Janus 颗粒亲水侧的行为特征
与液滴碰撞Janus 颗粒疏水侧的表现有所不同, 液滴碰撞Janus 颗粒亲水侧后, 液滴的行为特性在0 < t < 3 ms 内, 表现为铺展特性; 但在t > 3 ms 中, 与碰撞疏水侧呈现出截然不同的现象, 液滴在达到最大铺展长度后只有小幅度的波动, 并不会呈现回弹现象, 如图4 所示.
为了更加清晰表达液滴撞击亲水侧的铺展因子变化, 图5 给出了液滴在4 种韦伯数下撞击Janus 球颗粒表面的情况: 在0—3 ms 内, 液滴以碰撞点为中心向球面四周快速铺展; 在3—12 ms内, 与液滴碰撞疏水侧的行为明显不同的是液滴在达到最大铺展长度后, 并没有呈现出指数下降的趋势, 而是发生振荡现象.且最大铺展因子γ 值不同,We = 2.7 时, γ = 0.91; We = 30 时, γ = 1.77.发现相邻We 的最大铺展因子差值不同 (H1> H2>H3), 汪焰恩等[23]对液滴正向撞击亲水球面的过程进行了数值模拟, 可发现在不同We 下达到最大铺展系数时所需时间较为接近, 且最大铺展因子γ 值不同.即最大铺展因子随着We 的增大, 差值H 会逐渐减小, 表明γ 的变化程度主要受惯性影响.
3.3 液滴碰撞Janus 颗粒亲疏水分界线的行为特征
图6 展示了液滴碰撞Janus 颗粒亲疏水分界线的动态特性, 在0—3 ms, 液滴在亲水侧和疏水侧都表现为铺展特性, 达到最大铺展长度时所需时间相同; 在3—8 ms, 分界线两侧开始呈现出截然不同的现象, 分界线左侧液滴依然铺展在球颗粒表面, 而右侧液滴开始收缩团聚成椭圆形液滴 (We =30, t = 5 ms); 随着时间增大, 可发现右侧液滴脱离球表面, 在t = 6.5 ms (如图6 所示) 蓝色箭头所示, 处于腾空状态, 铺展和回弹现象同时发生.造成这种现象的原因为左右两侧的亲疏水差异, 使两侧液滴受力不同.

图4 不同We 下液滴碰撞亲水侧球面行为的动态过程Fig.4.Dynamic behavior of droplet collision on the hydrophilic spherical surface under different We..
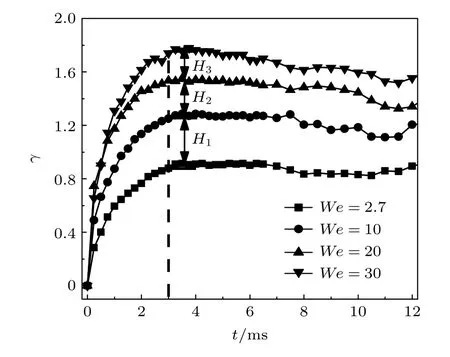
图5 不同We 下的动态铺展因子变化(亲水侧)Fig.5.Dynamic spreading factor of droplet collision under different We (hydrophilic side).
而图7 更加充分的展示了液滴碰撞Janus 颗粒亲疏水分界线的具体情况, 在Janus 颗粒亲水侧γ 随时间逐渐增大然后有小幅度的波动现象, 表明液滴亲水侧表面过程后期会发生小幅度的波动(回弹-铺展-回弹过程); 而在Janus 颗粒疏水侧γ 随时间逐渐增大, 达到最大铺展长度时呈指数减小, 表明液滴在疏水侧表面快速铺展后会发生回弹现象.随着We 的增大, 在液滴铺展初期Janus 颗粒亲水侧和疏水侧的γ 值基本一致, 但随着时间的增加二者之间的差值也逐渐增大, 此外两侧重合时间也随We 增大而增大: We = 2.7 时, 重合时间为0.75 ms; We = 10 时, 重合时间为1 ms; We =20 时, 重合时间为1.5 ms; We = 30 时, 重合时间为1.75 ms.
造成上述现象的主要原因为γ 的变化趋势是由Janus 颗粒表面润湿性决定的, 而最大扩展因子γ 值的大小主要受液滴碰撞速度影响.We 越大,液滴撞击Janus 颗粒球表面的惯性动能越大, 即液滴在球面铺展的动能越大, 液滴在球面的最大铺展长度越大.
3.4 液滴在Janus 颗粒不同表面的受力
为了更好探究造成液滴具有不同行为特征的原因, 对液滴进行受力分析, 如图8 所示.
图8(a)为液滴刚接触颗粒球表面, 此时液滴只受重力 ( Fg) 、惯性力[24]( Ft) 和接触力[25]( Fcontact) ,它们的表达式为:
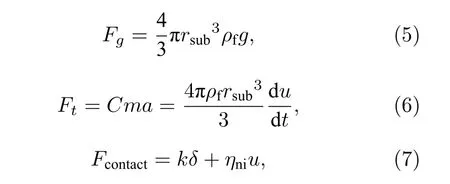
其中, rsub为颗粒半径, δ 为液膜厚度, ηni为球颗粒表面的碰撞系数,
可以发现液滴在初期铺展过程图8(a)和图8(b)中, 不管是碰撞Janus 颗粒亲水侧、疏水侧还是亲疏水分界线, 其在整个碰撞的过程所受的重力、惯性力和接触力基本一致, 且角 ϕ 几乎为零即表面张力可忽略不计, 从而使液滴在铺展过程初期γ 值几乎一致.
液滴在持续铺展图8(b)和图8(c)过程中, 液滴会在表面张力和黏性力的作用下铺展速度逐渐放缓, 但在疏水侧、亲水侧和亲疏水分界线3 种情况下液滴达到最大铺展长度时所需时间相等, 表明在此过程中表面润湿性对液滴铺展速率影响较小.

图6 不同We 下液滴碰撞亲疏水分界线行为的动态过程Fig.6.Dynamic behavior of droplet collision on the hydrophilic-hydrophobic boundary under different We..

图7 不同We 下的动态铺展因子变化 (亲疏水分界线) (a) 液滴在Janus 亲水侧的变化; (b) 液滴在Janus 疏水侧的变化Fig.7.Dynamic spreading factor of droplet collision under different We (the hydrophilic-hydrophobic boundary): (a) Dynamic spreading factor of droplet on the hydrophilic side; (b) dynamic spreading factor of droplet on the hydrophobic side.

图8 液滴在疏水侧、亲水侧和亲疏水分界线的受力Fig.8.Force analysis of the droplet on the hydrophobic side, hydrophilic side and hydrophilic-hydrophobic boundary.
图8 (c)—图8(e)为液滴的回缩过程表面张力为驱动力, 惯性力和黏性力为阻力, 作用在液滴接触线处受到的黏性阻力可以用Gennes[26]的润滑理论近似得出, 我们这里只考虑沿球面切线方向上的流体剪切运动, 因此黏性力为
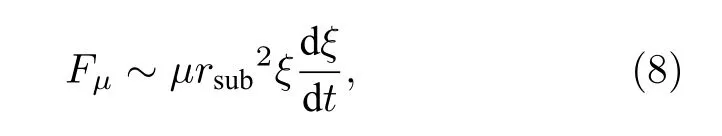
其中 ξ 为液滴在球颗粒表面的滑移长度.
此过程液滴在亲水侧、疏水侧和亲疏水分界线时的行为特性开始出现差别, 可发现亲水侧铺展长度随着时间的增加并没有大幅度的增加或下降趋势, 而是呈现出小幅度的上下波动现象; 而疏水侧液滴克服自身重力的影响形成“椭圆形”离开疏水表面; 液滴碰撞亲疏水分界线时, 分界线两侧的液滴呈现出截然不同的运动特性, 疏水侧的液滴受到亲水侧的牵引力跃向亲水侧.因此液滴离开疏水侧表面的主要原因是表面张力不同, 如图9 所示.
而线张力是研究液滴润湿行为的关键参数, 液滴三相接触线上的能量组成仅采用两相表面自由能无法解释清楚, 线张力的概念最早可以追溯到1878 年, Gibbs[27]研究发现, 液滴三相接触线上的能量组成仅采用两相表面自由能无法解释清楚, 为解决这一难题, 定义了一种类似于表面张力、在三相接触线上具有线性能量密度的作用力, 即线张力.1977 年, Pethica[28]定义了理想固体表面上液滴的线张力, 通过恒定体积下的能量最小化分析推导出修正Young 方程:
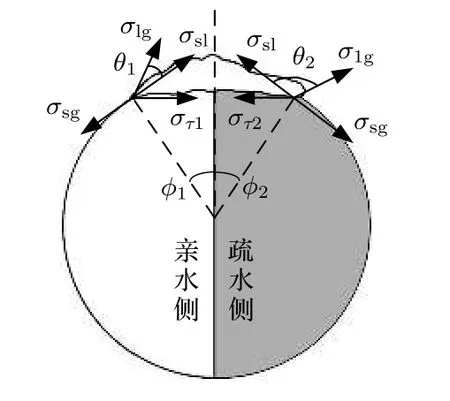
图9 球面的线张力效应Fig.9.Line tension effect of sphere.
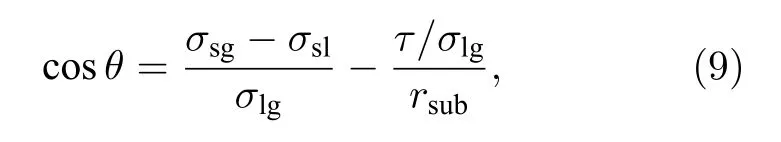
其中, θ 为Young 接触角, σsl、 σsg和 σlg分别为固液表面张力、固气表面张力和气液表面张力.且Guzzardi 和Rosso[29]推导出张力分量 στ:

根据(9)式和(10)式可推导出理想固体球表面上液滴的线张力, 亲水侧三相接触点沿固液界面切线方向受力平衡为
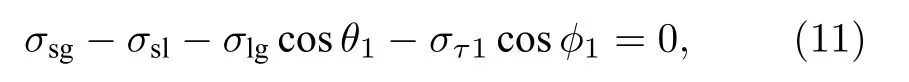
其中, θ1为Young 接触角, ϕ1为线张力所对应的张力分量 στ和固液表面张力 σsl的夹角.
疏水侧三相接触点沿固液界面切线方向受力平衡为
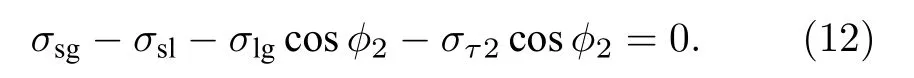
其中, θ2为Young 接触角, ϕ2为线张力所对应的张力分量 στ和固液表面张力 σsl的夹角.
根据(11)式和(12)式可得:
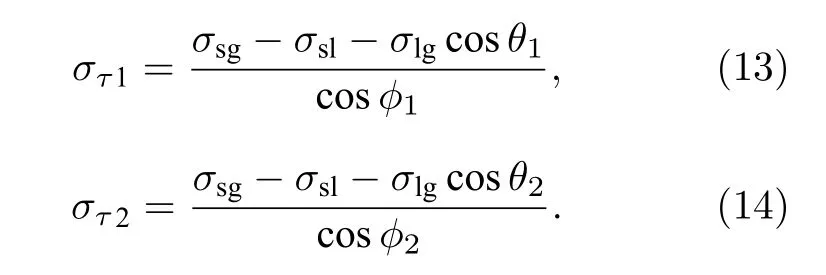
液滴碰撞亲疏水分界线 (如图7 所示), 在达到最大铺展因子前在两侧的铺展长度基本相等, 即ϕ1≈ϕ2, 且 因 为 θ1<π/2<θ2, 代 入(12)式 和(13)式可得 στ1<στ2, 故液滴由于牵引力的作用从疏水侧弹跳到亲水侧, 进而导致随着时间的增大两侧之间的铺展因子γ 差值也逐渐增大, 直到疏水侧液滴完全跳跃到亲水侧.
4 结 论
在不同We 下, 探究了液滴碰撞Janus 颗粒疏水侧、亲水侧和亲疏水分界线时的行为特征, 并进行了机理分析, 具体结果如下:
1) 液滴碰撞Janus 颗粒疏水侧时, 铺展系数γ 随时间增大会出呈现类似“抛物线”形状, 且不同We 下达到最大铺展因子所需要的时间较为接近.
2) 而当液滴碰撞Janus 颗粒亲水侧时, 铺展系数γ 随着时间的增大而逐渐增大并趋于稳定, 且最大铺展因子随着We 的增大也增大.
3) 但当液滴碰撞Janus 颗粒亲疏水分界线时,分界线两侧呈现出截然不同的运动特性, 液滴铺展和回弹会同时发生, 且疏水侧液滴会弹跳到亲水侧.而铺展系数γ 的变化趋势由表面润湿性决定,大小则主要受液滴惯性影响.且对两侧液滴受力分析发现亲水侧线张力小于疏水侧, 即 στ1<στ2, 进而导致了疏水侧液滴弹跳到亲水侧.
4) 液滴动能和表面能的互相转化是液滴铺展和回弹的关键, 液滴在碰撞Janus 球表面时, 会在重力、惯性力、表面张力、黏性力和接触力等力的综合作用下展示出其独特的行为特征.

