基于ARMA-SVM 组合模型的售电用户用电量预测方法

曹敏 巨健 白泽洋 刘骏涛

（1 国网陕西省电力公司 陕西西安 710048 2 苏文电能科技股份有限公司 江苏常州 213000）

相关学者已经对用电量的预测进行了深入的研究， 取得了显著的成果。 文献［4］和文献［5］在传统的灰色预测模型的基础上，提出了改进的灰色模型电量预测方法；文献［6］和文献［7］将偏最小二乘回归分析方法用于中长期电力负荷预测；文献［8］和文献［9］将神经网络方法应用于电力预测当中。

除了上述方法外， 另外最具代表性的就是自回归移动平均（Auto-Regressive and Moving Average Model，ARMA）模型和支持向量机（Support Vector Machine，SVM）模型。 已经有许多研究将它们应用于电力预测当中［10-11］。ARMA 模型由自回归模型（AR）和移动平均模型（MA）组成，采用历史数据和白噪声序列进行预测， 是一种精确度较高的线性时间序列预测模型。SVM 模型是根据统计学理论提出的一种机器学习方法， 是一种性能优异的非线性分析模型。 用电量预测的不确定性主要是因为影响其预测结果的各种内在和外在因素较多， 只通过单一的线性或者非线性描述进行预测的结果精准度较低。 因此本文提出一种基于ARMA 和SVM 模型的用电量组合预测方法，对售电公司下用电企业的用电量进行预测，通过将预测结果与单一ARMA 和SVM 模型的预测结果进行比较，验证本文模型的有效性和可行性。

1 模型介绍

1.1 ARMA 模型

自回归移动平均模型的预测过程有模型定阶、参数估计、求解等步骤。 模型的数学表达式为：

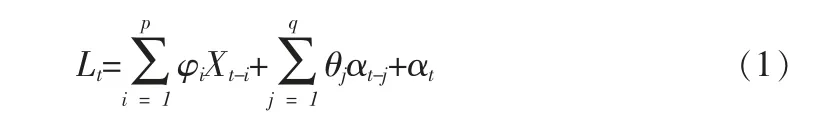
式中：Lt为预测结果，i（1≤i≤p）和θj（1≤j≤q）为系数，p、q 分别为自回归部分模型和移动平均部分模型的阶数，αt是白噪声序列，Xt是历史数据序列。

预测结果与前p 次的历史数据有关， 同时也受到前q 次以及当前的随机干扰项的影响。

采用从低阶到高阶逐步试探的方法确定模型阶数， 并确定最优参数。 根据已确定的阶数和参数，得到最优模型，得到t时刻的线性部分的预测结果Lt。

4）水利部门资料。水利普查成果等资料，可作为地理国情信息普查中水体、水工设施信息获取的重要辅助资料，提高普查结果精度。水利部门的流域单元边界数据及流域单元名称，河流空间分布数据及相关属性信息，湖泊空间分布数据及相关属性信息，水库、塘坝属性；水电站、水闸、堤防名称及编码、级别属性；取水口、地表水源地、入河湖排污口的空间分布数据及相关属性信息；水文站和水位站空间分布数据，为地理国情普查数据采集及统计分析提供数据来源。

ARMA 模型对线性数据的处理较有优势， 但是对非线性数据的信息较难捕捉， 其预测只考虑时间序列本身的变化规律，几乎不考虑其它相关变量的变化情况，而现实中的时间序列受到众多非线性因素的影响且含有复杂的噪声， 其确定的阶数和参数往往并非最优，从而导致预测精度不高。

1.2 SVM 模型

支持向量机模型的预测过程包括支持向量确定、 核函数选择、核参数确定、求解等步骤。 模型的数学表达式为：

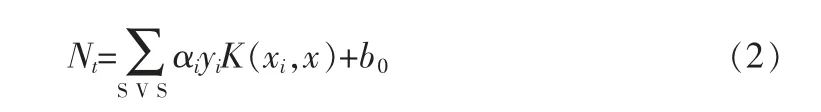
式中：SVS 为支持向量个数，αi为每个训练样本的拉格朗日系数，yi（-1 或1）为向量标签，K（xi，x）为所选择的核函数，b0为偏置量。 核函数代替了传统线性方程中的线性量，将数据映射到高维空间处理， 选择合适的核函数直接影响预测模型的性能和准确性，完成核函数的选择后，计算核函数的最优核参数，随后对样本进行训练预测，建立SVM 模型，求得相关参数，最终得到预测结果Nt。

SVM 模型在解决非线性、小样本、高维数的模式识别方面具有良好的泛化能力，其得到的最优解具有全局性，解决了其它算法中无法避免的局部最优问题。 但其预测效果对核函数的选择较为敏感，学习能力由核函数的类型和参数决定，对于大样本数据较难得到理想的训练效果， 需要提升其泛化能力和训练效率。

2 ARMA-SVM 组合模型

售电公司下用户的用电量受到众多因素的影响， 由于其为月度统计， 因此以年为单位会呈现一定的周期性规律，ARMA 作为1 种时间序列方法，可以较好地对用电量的线性相关性做出预测。 同时，用户的用电量还受到用电负荷、温度、计划用电量等因素的影响， 且这些因素之间也有着错综复杂的关系，将这些因素作为变量输入SVM 模型进行非线性回归，可以较好的完成对用电量非线性部分的预测。

本文针对售电公司用户用电量的预测问题， 基于ARMA和SVM 模型采用1 种组合的预测方法， 把用电量时间序列看成由线性自相关结构和非线性结构两部分构成， 分别发挥ARMA 模型和SVM 模型对线性模型和非线性模型处理的优势，将二者组合进行用电量的预测。 通过组合模型进行预测的具体步骤如下：

（1）获取历史用电量实际数据；

（2）构建ARMA 模型得到t 时刻的线性部分的预测结果Lt；

（3）重复步骤（2），对最后n 个样本进行预测，得到预测结果序列L；

（4）将上一步得到的预测结果序列L 与历史用电量数据相减，得到残差序列N；

（5）获取负荷、计划用电量、温度的历史数据；

（6）将步骤（5）获取的数据与步骤（4）得到的残差序列N进行归一化处理：

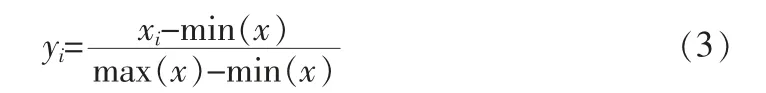
式中：yi为归一化结果；xi为原始数据；max （x） 为最大值；min（x）为最小值。

（7）得到归一化后的数据集，作为SVM 模型的样本集；

（8）选择核函数，确定SVM 参数，生成预测结果Nt；

（9）将线性部分预测结果Lt和非线性部分预测结果Nt组合，得到最终预测结果Yt=Lt+Nt。

通过组合模型进行用电量预测的流程图如图1 所示。

3 算例对比分析

本文采用的实验数据来自某售电公司的用户用电数据，将5 家用户企业的历史用电量数据以及用电负荷、温度、计划用电量等相关数据作为样本数据输入， 根据第2 节所述步骤建立预测模型，并利用模型预测用户企业的每月用电量数据。依次采用ARMA 模型、SVM 模型和ARMA-SVM 组合模型对5家用户企业的用电量分别进行预测， 并对比分析这3 种模型的预测效果。

为考察用电量的预测效果， 本文选取平均绝对百分误差（Mean Absolute Percentage Error，MAPE）作为定量反映模型预测精度的指标，其计算公式如下：

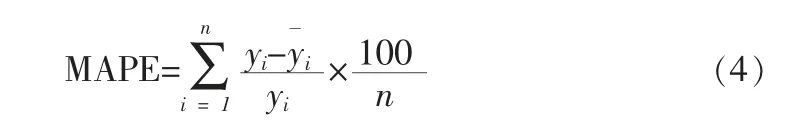
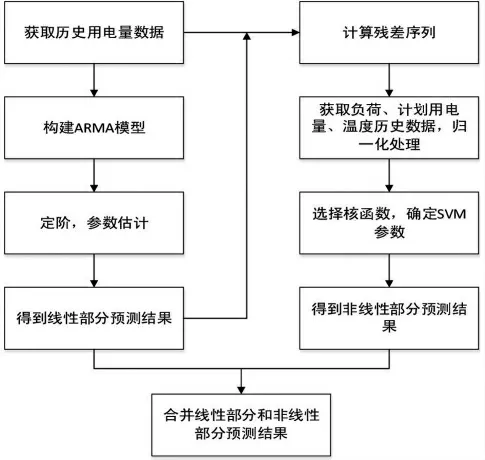
图1 组合模型预测过程

式中：yi为实际用电量，为预测用电量，n 为实验样本的总数量，MAPE 值越小，说明预测值与实际值的差异越小，预测精度越高。

以用户企业A 为例，分别用ARMA、SVM 和组合模型对其连续24 个月的用电量进行预测，将预测结果与其实际用电量进行对比。

用户企业A 从2016 年1 月至2018 年12 月各月份的实际用电量数据如表1 所示。

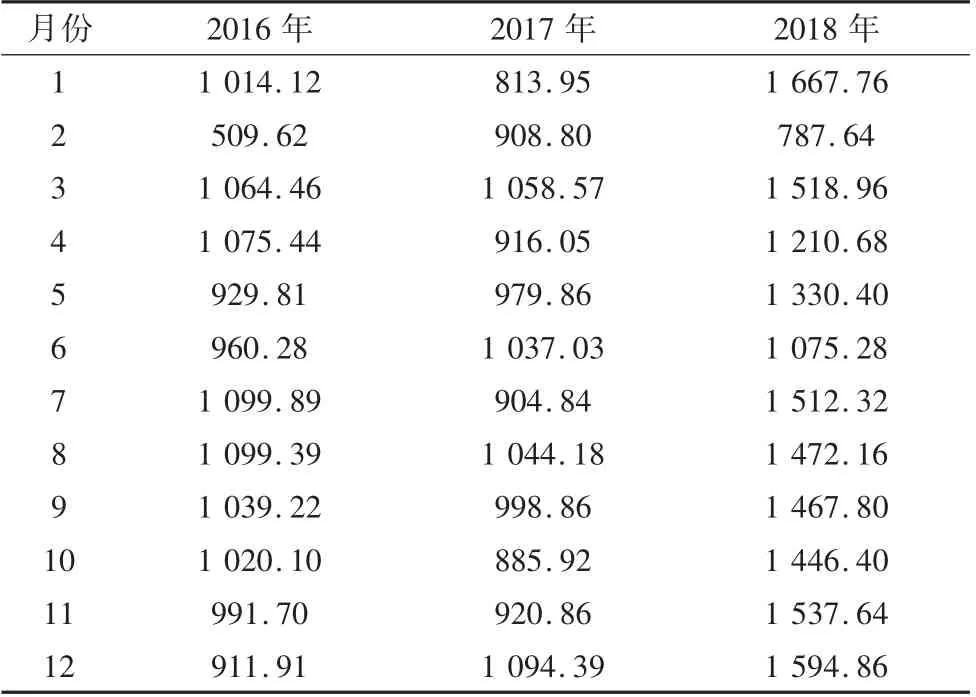
表1 用户企业A 实际用电量数据 单位：MWh

分别利用ARMA、SVM 和组合模型的预测结果与实际用电量的对比如图2～图4 所示。

A、B、C、D、E 5 家用户企业分别用ARMA、SVM 和组合模型预测的结果与相应的实际用电量计算出的MAPE 值对比情况如表2 所示。

表2 预测结果的MAPE 值情况

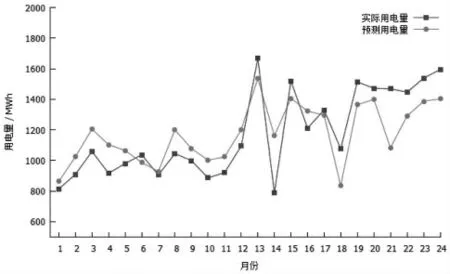
图2 ARMA 模型预测结果与实际用电量对比

图3 SVM 模型预测结果与实际用电量对比

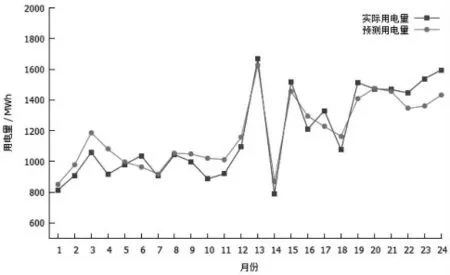
图4 组合模型预测结果与实际用电量对比

通过对比结果可以看出，SVM 模型的预测结果普遍优于ARMA 模型， 这说明了非线性因素的作用对用电量的预测有关键的影响，特别是在数据波动较大时（如春节期间用户用电量下降趋势明显），SVM 模型的预测更加精准，而ARMA 模型更适用于较为平稳的训练数据。而综合了ARMA 和SVM 的组合模型预测精度普遍优于单一的ARMA 和SVM 模型，有较好的稳定性，说明其充分利用了原始数据中的信息，避免了单一模型的局限性， 验证了综合考虑线性和非线性作用的组合模型的合理性与必要性。

4 结论

售电公司作为电力市场的新兴主体， 其对用户用电量预测的准确性是关乎其减少偏差考核风险和提高竞争力的关键。针对用电量预测的线性和非线性特征，本文利用ARMA 模型捕捉其线性趋势，利用SVM 模型预测其非线性规律，据此建立ARMA 和SVM 的组合模型， 对用户企业的用电量进行预测。 实验结果表明，组合模型既兼顾了单一预测模型各自的优势，又弥补了彼此的不足，相较于单一的ARMA 和SVM 模型，其预测结果具有有效性和更高的精确性， 可以为售电公司的预测用电量工作提供很好的技术支持。