车路协同下基于冲突规避的匝道合流优化控制方法

陈润超

(厦门市城市规划设计研究院有限公司 厦门 361012)

驶入匝道瓶颈的汇入行为是强制性换道行为，瓶颈点是快速路连续流交通设施的咽喉，驾驶员的换道行为是触发瓶颈失效的因素之一。减少匝道合流过程中的冲突、控制匝道车辆汇入过程的换道行为有利于瓶颈区域的车辆有序行驶。而车路协同技术(cooperative vehicle infrastructure system, CVIS)为车辆合流过程的冲突识别及驾驶员换道行为指导提供了技术支持。

CVIS环境下的匝道控制方法研究一直受到学者们的关注。文献[1]以车辆的燃油经济性最优为目标提出了合流区智能车辆集中控制的方法。文献[2]考虑了主线车速调节和车辆换道因素，提出基于车路协同的匝道车辆汇入引导方法。文献[3]提出了一种车联网环境下的交叉口冲突管理算法。文献[4]针对匝道合流区搭建了智能网联车辆控制方案并验证了方案的有效性。文献[5]以车辆油耗和行程时间最优为目标提出了一种匝道合流的自动驾驶车辆协调方法。从现有的研究来看，主要集中主道和匝道车辆间隙的关系，对于冲突管理的角度考虑较少。

本文通过分析匝道合流区域的车辆合流过程，以冲突规避为原则，提出了一种CVIS环境下的匝道合流优化控制方法，以期降低合流区的冲突，避免车辆在合流过程中走停带来的安全隐患。

1 冲突规避方法

图1为车辆合流场景，主道和匝道交叉的区域称为合流区。匝道车辆在合流区向主道汇入，汇入的过程中与主道车辆可能会存在冲突。

图1 车辆合流场景

按照先到先服务的原则，智能车辆需要调节自身车辆的加速度以顺利依次通过合流区，降低发生冲突的风险。图2为车辆在合流时空轨迹图，假设合流区上游的车辆通过合流区的运行轨迹见图2，xi(t)为车辆随时间变化的轨迹,ti(o)为车辆i到达冲突区的时间，ti(d)为车道离开冲突区域的时间。其中车辆的速度为vi，加速度为ai，以车辆i为例，在经历了t时间后距离车辆起始位置的位移计算方法见式(1)。

xi(t)=xi(0)-0.5ait2-vi(t)

(1)

式中：xi(0)为t=0时车辆i的初始位置。

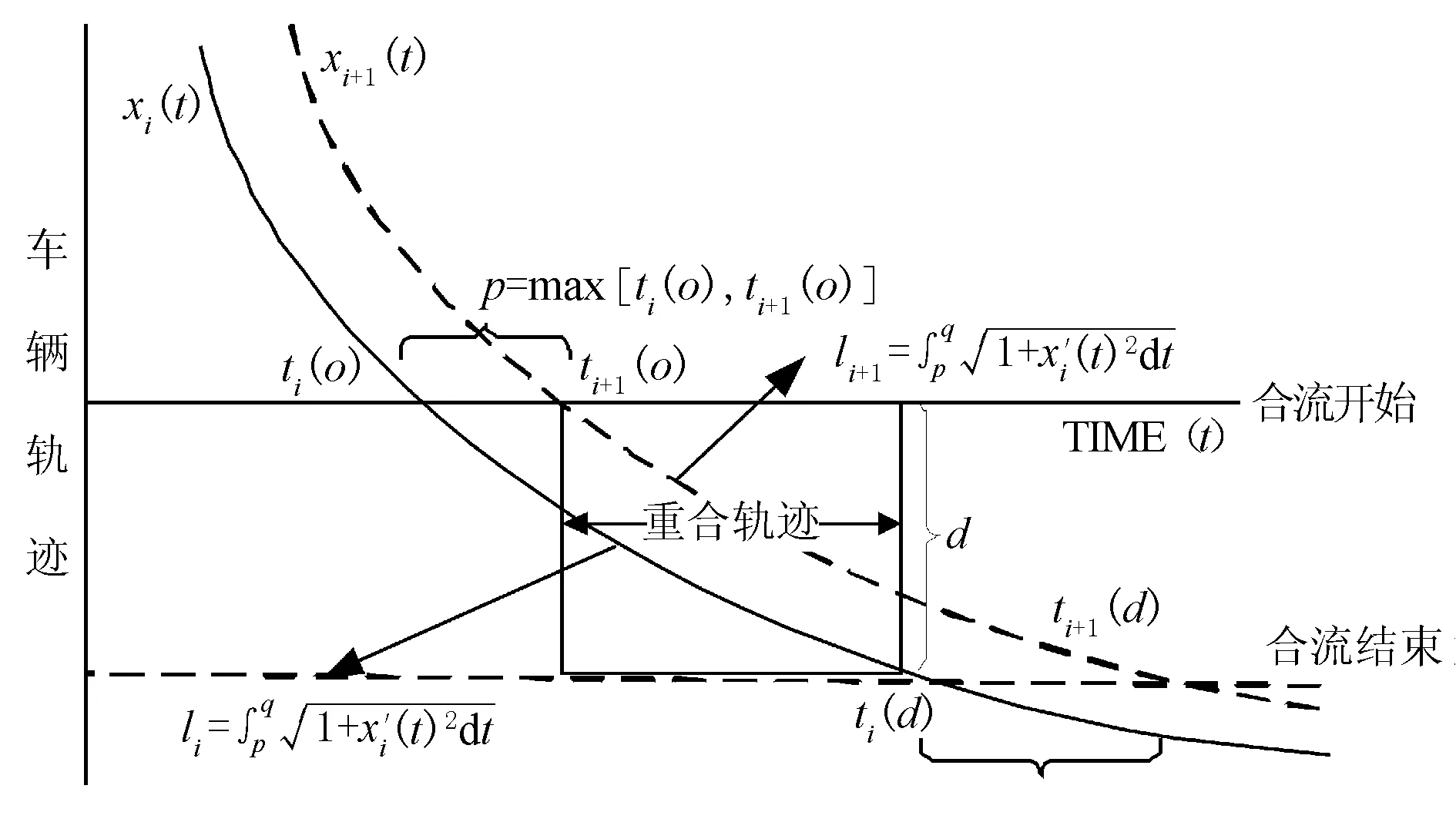
图2 车辆在合流区的时空轨迹图

p为车辆i与i+1到达匝道合流区的最晚时间；q为车辆与离开匝道合流区的最早时间；li与li+1分别为车辆i与i+1在重叠区域的曲线长度。如果p>q，则li与li+1不存在，两车不会同时出现在合流冲突区，也就没有发生冲突的可能。因此，车辆在匝道合流区域的时空轨迹重叠越小，处于合流区域的车辆就越不容易发生事故，车辆也就越安全。车辆i重合的轨迹长度l的计算方法见式(2)。

(2)

因此，可以把匝道合流区域内车辆的安全协作问题转化为合流区域内时空轨迹图的曲线长度问题。

2 基于冲突规避的车辆控制方法

2.1 控制场景搭建

CVIS环境下车辆合流过程见图3。

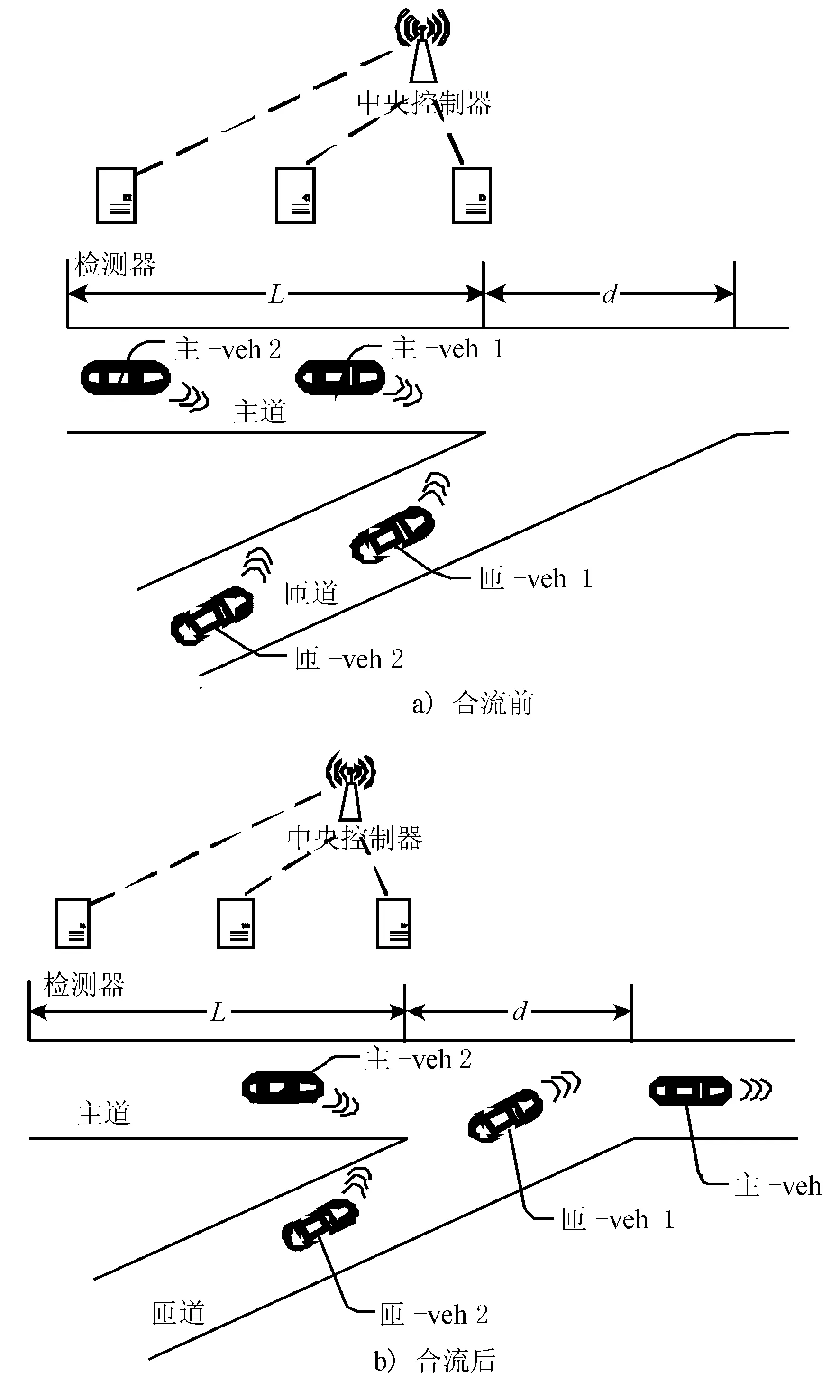
图3 CVIS环境下车辆合流过程

由图3可见，合流区长度为d，合流控制范围为合流区上游长度为L的区域。传统合流路段的车辆通行是受信号灯或交通标识控制的，这就意味着合流的其中一方必须停车等待，而后才能通行。在CVIS环境下，路侧检测器收集周围车辆的行驶信息(包括车辆位置、速度、加速度)，发送至中央控制器处理，中央控制器将后续的行车指令发送给相应车辆，实现主道和匝道车辆的协同合流。

2.2 车辆动力学模型

车辆运动学方程为

设T为离散时间的1个步长，则得到离散化的车辆运动学模型如下。

式中：Δv为车辆的加速度；x(i)为第i个时间步的车辆位移；v(i)为第i个时间步的车辆速度。

2.3 车辆合流的优化控制模型

2.3.1控制目标

在匝道合流过程中，控制的目标为合流区的车辆轨迹重合最小，即

式中：m,n分别指主道和匝道的车辆，m=1,2,…,M;n=1,2,…,N；ti指第i个时间步；x为车辆的轨迹的微分，即车辆速度。

2.3.2约束条件

1) 车辆间安全间距约束。

xk(ti)-xk-1(ti)≥G,k=m,n

式中：G为车辆行驶最小安全距离。

2) 车辆行驶速度约束。

0≤vk(ti)≤vmax,k=m,n

式中：vm(ti)、vn(ti)分别为第i个时间步的主道车辆m和匝道车辆n的速度。

3) 对车辆的运动过程进行离散化处理，主道、匝道车辆的位移约束如下。

式中：to,m、to,n分别为主道和匝道车辆进入合流区的时间；td,m、td,n分别为主道和匝道车辆离开合流区的时间；xm(t0)、xn(t0)为在初始时刻t0时，车辆m、n距离合流区起始点的横向位移；d为合流区的长度。

3 匝道合流优化控制仿真分析

3.1 控制参数设置

初始状态。

xm2(t0)=-100 m，xm1(t0)=-80 m；

xn2(t0)=-100 m，xn1(t0)=-80 m

所有车辆的初始速度均为5 m/s，初始加速度为0 m/s，d=20 m，G=10 m，vmax=8 m/s。

3.2 控制结果分析

通过对优化控制策略进行数值模拟，优化控制后行驶队列效果见图4，优化合流位移效果见图5。

图4 优化控制后行驶队列

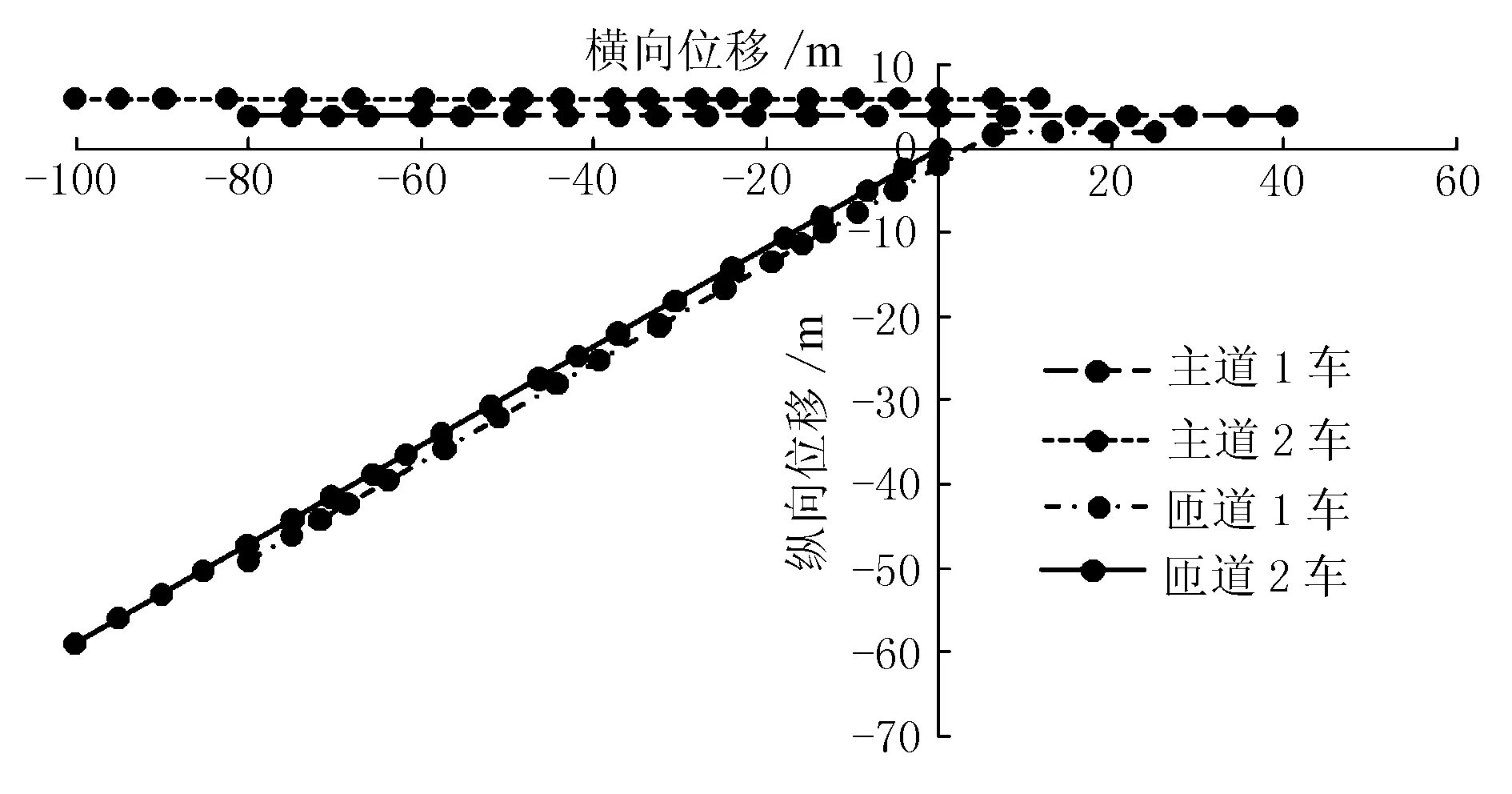
图5 车辆优化合流位移

由图5可知，在优化控制过程中，车辆轨迹比较分散，整个合流过程车辆间距均能保持10 m左右,最后在主道上能够使车辆实现较均匀排列行驶。表明在优化控制算法下，车辆可以按照一定的顺序合流，能够比较充分地利用道路资源，避免合流时车辆间冲突。

3.3 仿真验证

为验证控制策略的效果，数值模拟无控制下的合流过程，设置对照组。其参数设置和初始条件不变。

对照组车辆的合流位移见图6。

图6 对照组车辆的合流位移

由图6可知，在不控制情况下，车辆进入合流上游，其运行轨迹较为分散，靠近合流区时，车辆的运行轨迹较为密集，合流完成后，车辆排成一列继续行驶。整个过程中，车辆间距离保持在安全范围。表明在不控制条件下，车辆仍可完成合流，但是在合流区附近，车辆会发生拥挤，甚至停车等待。

为进一步比较不同条件下的车辆运行效果，选取2组仿真过程中所有车辆的平均速度、速度标准差和加速度标准差进行对比分析。

控制组和对照组的车辆速度、加速度图见图7，车辆仿真指标表见表1。

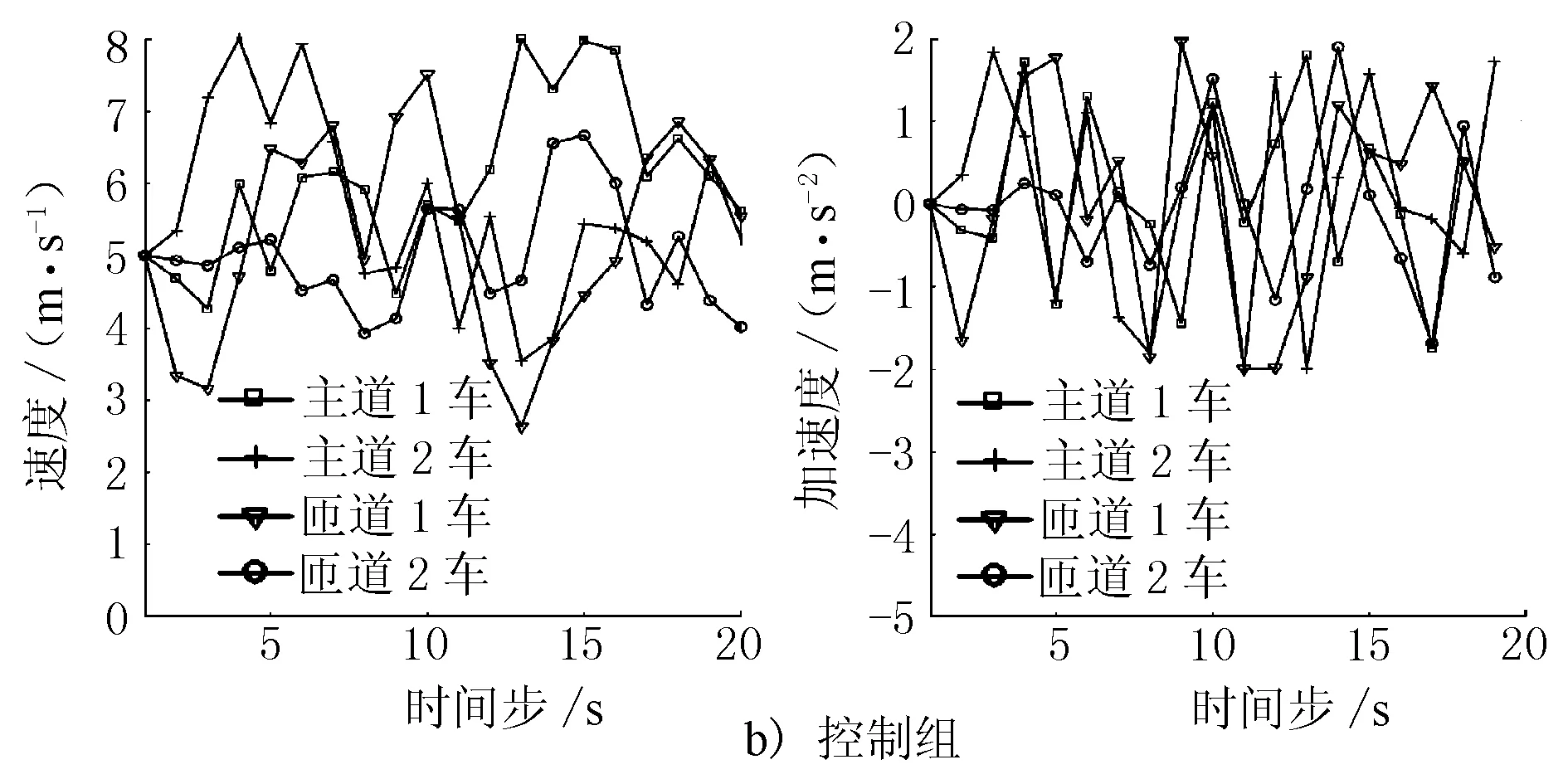
图7 车辆速度和加速度

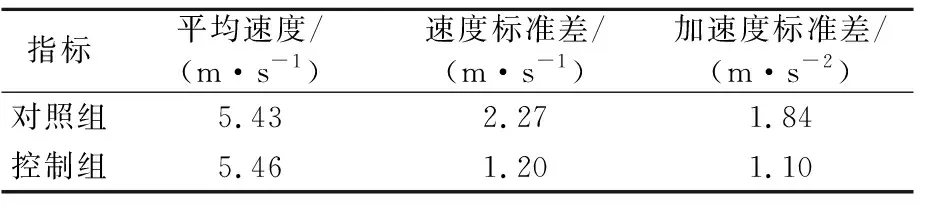
表1 车辆仿真指标

由图7及表1可知，2组平均速度基本相同，这表明实施控制策略不会降低合流区车辆的运行速度；速度标准差方面，对照组的车辆速度波动较大，为2.27 m/s，特别是靠近合流区附近，而控制组的车辆速度波动较小，运行相对平稳，为1.2 m/s，表明实施控制策略有利于平稳车辆速度，降低车流的波动；且由加速度标准差可见，对照组的车辆加速度在合流区附近波动较大，为1.84 m/s2，控制组车辆的加速度维持在-2～2 m/s2区间，为1.10 m/s2，表明实施控制策略能够增强车辆行驶的舒适性，不会出现突然加速和急停的情况。

4 结语

本文以匝道合流区为研究对象，根据合流区的特性，以冲突最小为目标，构建了匝道合流区优化控制模型，并进行了数值仿真，表明本文的控制方法能够使得车辆在避免冲突的前提下顺利合流。随后将其与无控制匝道合流进行对比，以车辆平均速度、速度标准差、加速度标准差为指标进行评价分析，发现控制策略下车流更加稳定，车辆行驶的舒适性、安全性有所提高，表明匝道合流优化控制方法具有一定的现实意义。

本文在研究过程中将匝道合流区的合流情况有所简化，一些问题仍需进一步的研究。比如，讨论更多车辆的合流情况，多车辆合流冲突会增多，也许会更加凸显优化控制的优势；另外在合流过程中多车道间车辆的换道过程本文也未讨论。