施工荷载作用下岩质边坡稳定性及影响因素研究
满 立 徐伟忠 庞劲松
(1.同济大学道路与交通工程教育部重点实验室 上海 201804; 2.上海城建市政工程(集团)有限公司 上海 200065)
边坡稳定问题一直是相关学科关注的重点,多样的演化规律使其难以形成统一的控制标准。针对公路边坡施工风险,魏小楠[1]考虑了岩土体材料在施工扰动等因素作用下表征的应变软化特性,通过数值计算,揭示了路堑边坡渐进性破坏过程,指出滑裂面强度的折减速率与剪应变增量有关;郭建军[2]分析了岩质边坡中,顺层边坡与反倾边坡的案例,基于室内模拟试验,揭示了反倾岩质边坡次生倾倒的形成过程和灾变机制;宋杰等[3]基于LiDAR扫描技术和模糊聚类分析,对边坡岩体出露的结构面进行识别和统计,获取其空间几何信息用于数值模型构建;刘红岩[4]采用FLAC中的弹脆性模型和Null模型描述完整岩体和宏、细观缺陷,计算分析了两类缺陷对边坡岩体力学特性的作用机制;蒋明镜等[5]利用植入微观接触模型的离散元软件,实现边坡失稳过程的演化模拟,表明顺层岩质边坡的滑裂面由共面节理贯通破坏形成,反倾岩质边坡则由非共面节理贯通破坏形成;樊炼等[6]分别采用强度折减法和极限平衡法计算开挖对边坡稳定性的影响,结果表明边坡开挖施工,其稳定性逐步提高;Penalba、向茂等[7-8]基于可靠度和可变模糊集理论等数理方法,进行边坡失稳风险评估和成本预测,并对公路高边坡开挖风险进行了评价。
已有研究主要聚焦于边坡的整体失稳破坏,较少结合具体施工过程,探究其对边坡的影响。本文通过有限元数值计算,分析开挖施工中,岩质边坡的稳定状态及不同影响因素的作用效果。
1 计算理论
现有的边坡稳定性计算方法中,以Morgenstern-Price法最为严谨,其在静力平衡要求、滑裂面性状等方面均不作任何假定。但该方法基于Mohr-Coulomb破坏准则,并不适用岩质边坡;而更为适用于岩体的Hoek-Brown破坏准则,在边坡安全计算中,又缺乏与具体方法的结合。本文首先将Hoek-Brown破坏准则的判据融入Morgenstern-Price法的原理推导中,实现对岩质边坡工程的准确判断。
为计算抗剪强度-法向应力曲线,需要4个参数分别为:σci,岩块单轴抗压强度;mi,岩块性状;GSI,地质强度指标(0~100);D,岩体扰动因子(0-1)。
用D、GSI、σci和mi计算中间参数mb方法见式(1)。
(1)
曲线参数α和s计算方法分别见式(2)、式(3)。
(2)
(3)
原岩的GSI为100,此时s为1.0。在早期的破坏判据中,参数α假设为常数0.5。现在认为它是一个与GSI相关的变量。
破坏时,主应力计算方法见式(4)。
(4)
式中:σ1,σ3分别为第一、第三主应力。
通过一系列给定的σ3来计算σ1,从而建立强度曲线。
σ3缺省范围从岩石抗拉强度值(负值),到单轴抗压强度值的50%。抗拉强度计算方法见式(5)。
(5)
基于破坏时的σ1-σ3值,τ-σn数据点计算方法见式(6)~(8)。
(6)
(7)
(8)
由软件计算每个条块底面的法向应力,找出样条曲线的斜率,作为材料的内摩擦角,将曲线的切线延长到τ轴,截距设为黏聚力。这样每个条块都有不同的c、φ值,将其代入M-P法计算边坡安全系数。
2 计算案例背景
依托工程为杭绍台高速公路,采用JTG B01-2014《公路工程技术标准》中双向四车道标准,设计车速100 km/h,路基标准宽度26.0 m,汽车荷载为公路-I级。计算案例选取K157+250-K157+550处路堑边坡。
2.1 工程地质概况
工程位于浙东南低山丘陵区,山峦起伏,沟谷狭窄。受构造控制,河流、山脉走向多呈北-北东走向,沿线山体多在100至500 m之间。工作区以断裂构造为主,走向以北东向、北西向为主,所选取路堑边坡发育2组次级构造带:Fc46,产状198°∠64°;Fc47,产状24°∠73°,影响宽度约15 m,节理密集,构造面平直,岩体破碎。工作区地震强度弱、频率低、震级小,地震基本烈度小于IV度区。
该边坡岩性主要为凝灰岩、角砾凝灰岩,路基基底为强~中风化。沿线丘陵山体总体覆盖层较薄,自然山坡基本稳定。
2.2 现场工况
以K157+335处边坡断面为例,左侧分5级开挖,第一~四级坡高10 m,第五级开挖到坡顶,自下而上坡率分别为1∶0.75,1∶0.75,1∶1,1∶100,1∶1.25,各级间设置2 m宽碎落台。右侧分二级开挖,第一级坡高10 m,第二级开挖到坡顶,其坡率均为1∶1,各级间设置2 m宽碎落台。开挖过程自上而下进行,开挖一级防护一级,每级施工完成后约有5 d的间隔,进行坡面锚固结构的施工,锚固形式见表1。

表1 K157+335边坡断面锚固形式
3 数值计算模拟
3.1 基本假定
为便于计算,本文对所建立的边坡有限元分析模型进行假设简化,基本假定如下。
1) 边坡表层覆盖层较薄,忽略不计。各岩层层间完全连续,在各层交界面上,只考虑垂直方向上的摩擦与位移,不考虑接触面的穿刺问题。
2) 岩层材料的力学特征以弹性模量和泊松比等进行表征;凝灰岩及角砾岩,采用Mohr-Coulomb模型联合Hoek-Brown破坏准则进行描述。
3) 模型两侧施加水平(X)位移约束,模型底部施加双向(X和Y)位移约束;水平位移向右为正,向左为负;竖向位移向上为正,向下为负。长度单位除特殊标注外,默认为m。
4) 锚固结构等效为加固力,当加筋体的作用线和滑面相交时,将其视为作用在焦点的集中荷载。层间接触仅考虑摩擦作用。
3.2 模型建立
以K157+335处边坡断面构建计算模型,模型长165 m,模型最高72 m,考虑开挖,边坡净高52 m。边坡修筑形式及锚固结构已在前文叙述,计算模型见图1,共计2 315个节点,2 245个单元,5个特征点。
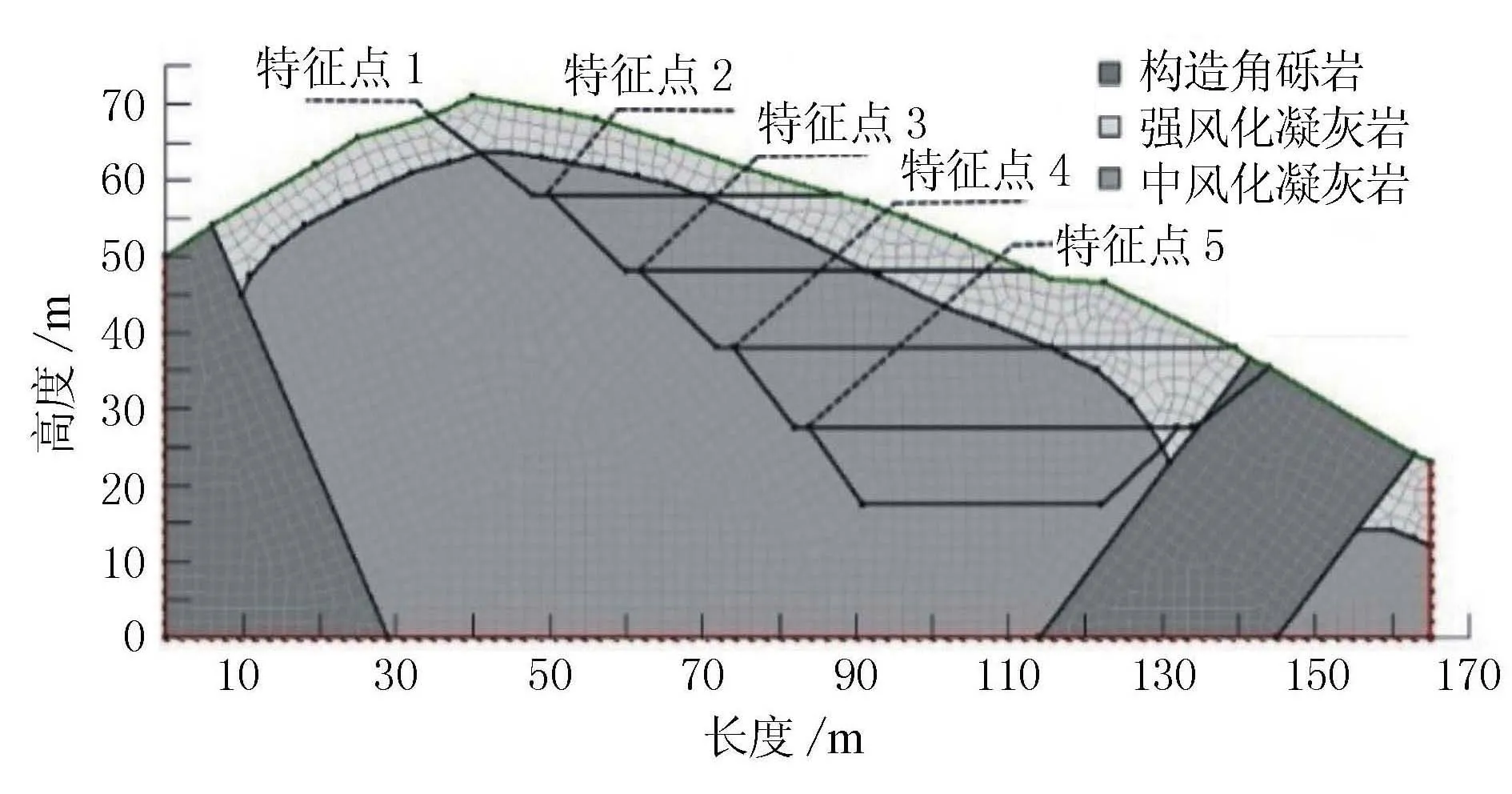
图1 有限元模型示意图
3.3 计算参数
本文的材料参数基于相关工程地质勘查报告、设计资料以及相应的土工试验获得,具体参数取值见表2与表3。

表2 材料弹-塑性参数
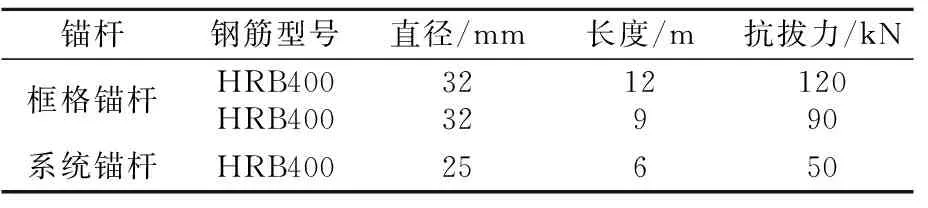
表3 锚杆性能参数
3.4 荷载施加与计算工况
首先计算路堑边坡长期作用下的力学响应,待其变形稳定后提取各点的应力值。利用提取的应力值作为边坡模型的地应力平衡初始应力输入量,将地应力平衡后的模型作为边坡模型的初始状态进行加载,初始最大剪应力分布云图见图2。
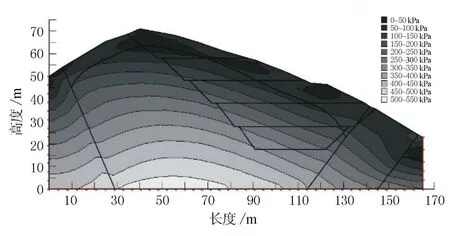
图2 初始最大剪应力图
分别计算不同施工间隔,即各级边坡开挖完成后的间隔时间和有、无锚固结构作用下边坡稳定性。施工间隔分别取3,5,8 d,锚固作用分为有、无锚固。取实际施工过程中的5 d间隔和有锚固作为标准工况,其他工况设定见表4。

表4 模拟工况
4 结果分析
4.1 边坡开挖变形规律
标准工况下边坡累计变形见图3。随着施工开挖的进行,边坡出现了明显的“应力释放”现象,在X方向和Y方向,位移均呈现背离坡体的趋势。其中,X方向位移前期呈向内发展的趋势,变形最大特征点1(即边坡顶点)的位移量约2 cm,在第三级边坡开挖后,位移方向出现了明显的背离坡体的趋势,位移量自上而下增加,大小为1.06~4.65 cm不等。
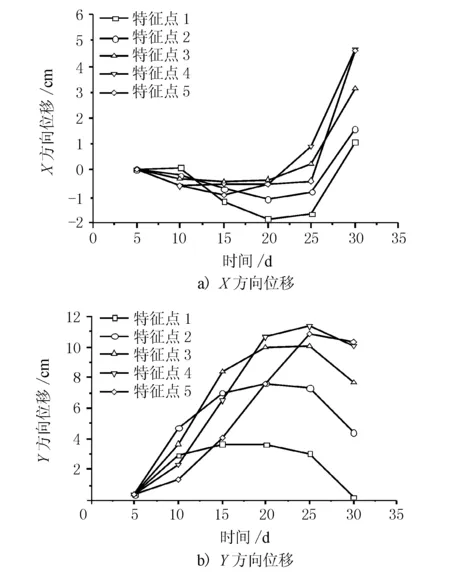
图3 特征点累计位移
随着应力释放的缓解和边坡结构的改变,Y方向位移变化由隆起变为沉降。变形量随着开挖深度的增加而增加,最大隆起值为2.67~11 cm,值得注意的是,各级边坡出现最大隆起的时间点是不相同的,越高处出现的越早,也更早进入下降区间。
总的来看,随着施工的进行,路堑开挖由较为松散的强风化层,过渡到高地应力的完整岩层,应力释放明显加强,背离的边坡的位移发展趋势开始凸显。但X与Y方向的变形机理并不完全一致,其变形过程也并非高度相关,需要结合具体情况进行分析。
施工完成后累计位移云图见图4。由图4a)可见,X方向位移主要集中在第三级边坡中部至第五级边坡中部区域,受开挖卸荷和应力释放叠加作用影响,最大变化量约为6 cm;Y方向位移也主要集中在上述区域,但沿高度方向分布更为均匀,最大变化量约为11 cm。综合认为在路堑边坡施工过程中,应特别注意中下部区域的变形状态,尤其在完整岩层开挖过程中,应防范由较大变形引发的岩质边坡局部剥落。

图4 施工完成后累计位移云图
该边坡岩体完整,且坡比较缓,其整体稳定性较好,整体滑塌的风险不高。安全系数变化见图5。
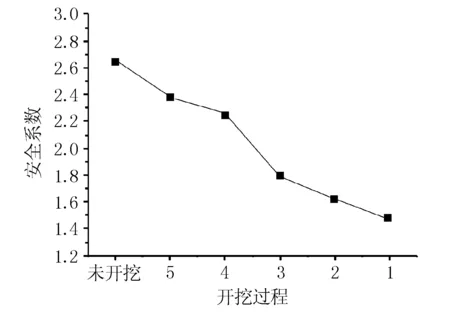
图5 开挖过程中安全系数变化
由图5可见,随着边坡开挖的深入,安全系数由2.66下降到1.47,降幅显著,其中最大降幅出现在第三级边坡的开挖过程中,这与前文分析的该处应力释放现象加剧相契合。虽然最小安全系数1.47较为可靠,但在计算过程中发现,中风化岩层中出现浅表层滑坡,这一现象应在该类边坡的施工过程中引起注意。
4.2 施工荷载影响因素与控制标准
在分析标准工况下边坡变形演化过程的基础上,进一步计算了开挖时间间隔及有无支护措施对边坡状态的影响。
4.2.1开挖间隔
开挖间隔分别设置为3,5,8 d,最大矢量位移(X与Y方向位移的平方根)见图6。随着边坡开挖的进行,矢量位移也随之增加,随后在第三级边坡开挖完成后趋于平稳。分析认为,施工时间间隔与最大矢量位移负相关,但这一趋势并不明显,其中3 d状态下,最大位移为12.12 cm;5 d状态下,最大位移为11.15 cm,即3 d的92%;8 d状态下,最大位移为10.39 cm,即3 d的85.7%。不难看出,随着施工间隔的增加,对边坡变形的缓冲作用也在下降。
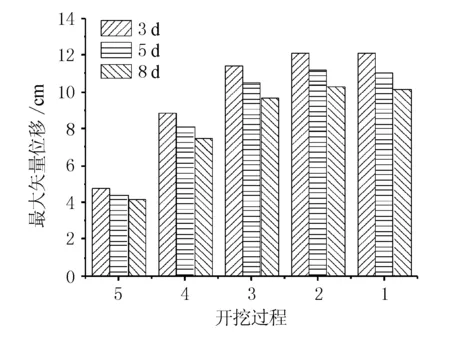
图6 不同时间间隔的开挖过程中最大矢量位移
不同时间间隔下安全系数的变化规律见图7。
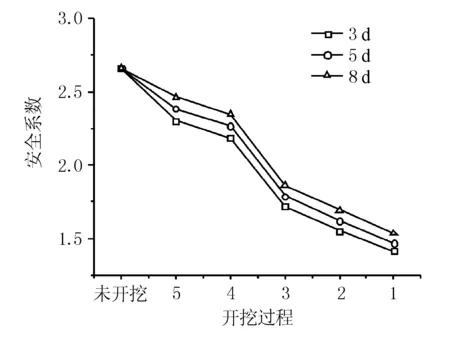
图7 不同时间间隔的开挖过程中安全系数变化
由图7可知,变化趋势基本相同,安全系数的下降速率与施工间隔负相关,即施工间隔越大,边坡安全系数的下降趋势越平缓,其最终值分别为1.533,1.465,1.412,相互之间的差别不超过±5%。可见施工间隔对边坡整体稳定性影响不大,在边坡施工安全能得到保证的前提下,应尽量选取较小的施工间隔,缩短施工工期。
4.2.2锚固作用
最大矢量位移见图8。

图8 开挖过程中最大矢量位移(有无锚固)
由图8可见,其变化趋势与前述相似,但有、无锚固对边坡变形量影响较大。相较于无支护状态下的13.38 cm,锚固结构可以使变形量减小16.6%,下降至11.15 cm。分析认为,锚杆结构对制约岩质边坡的变形量效果显著,应在高风险边坡的施工过程中加强应用。
有、无锚固状态下的安全系数变化见图9。
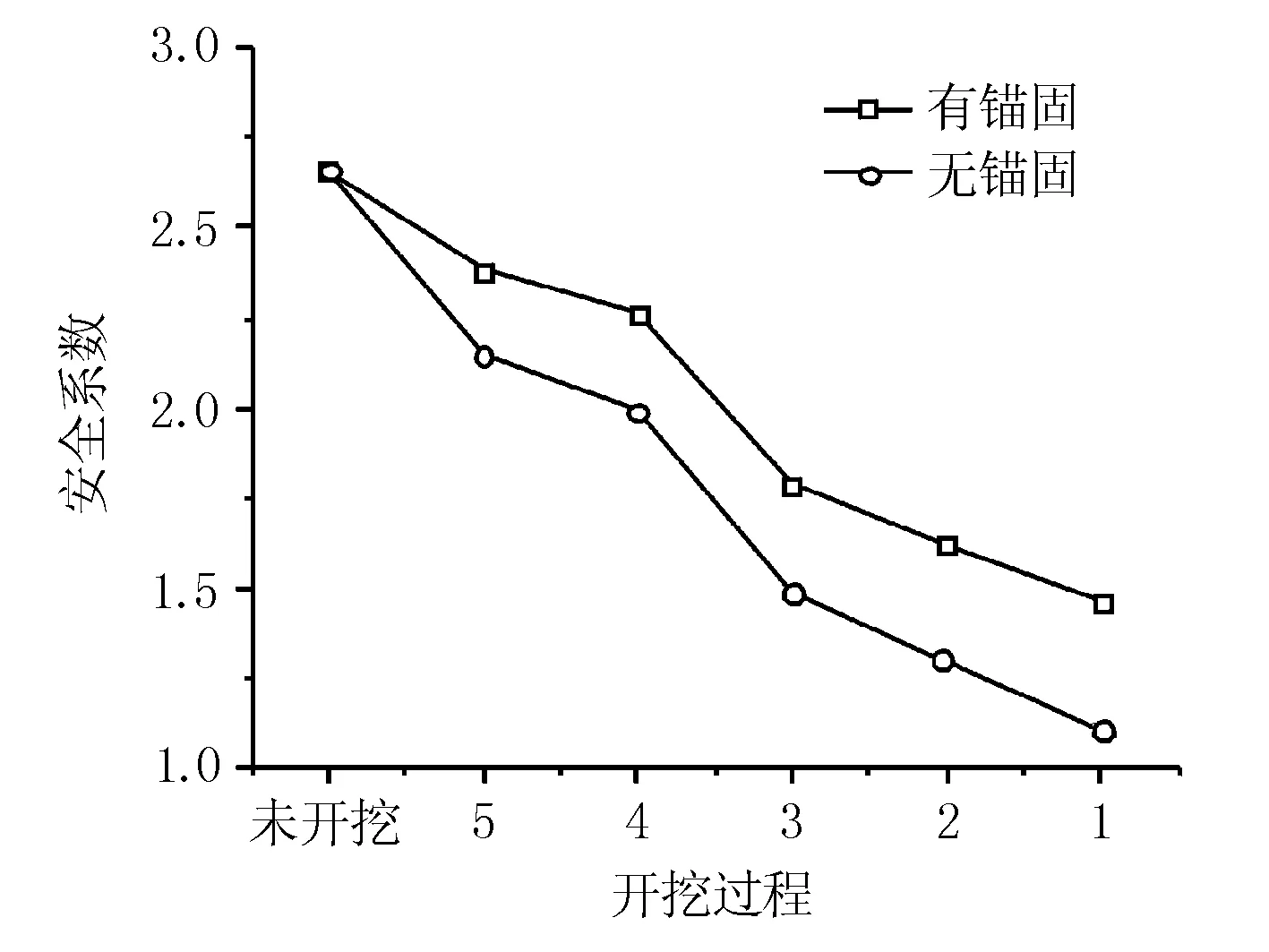
图9 开挖过程中安全系数变化
由图9可知,两者呈现出较大差别,随着开挖过程的进行,这一差别逐渐放大。在最后一级边坡施工完成后,有锚固作用下的边坡安全系数为1.47,对比无支护作用的1.11,提高了32%。故认为,锚固类的支护结构对提高岩质边坡整体稳定性起到显著作用。
5 结论
1) Hoek-Brown破坏准则较为适用于岩体,通过将其作为判据融入Morgenstern-Price计算方法,可实现对岩质边坡工程的准确计算,文中未体现的现场监测数据与标准工况数值计算结果基本一致。
2) 对于低风化的凝灰岩质边坡,随着开挖后地应力的释放,边坡变形整体呈现背离坡体的趋势,从时间上看,X方向前期较为平稳,后期明显外凸,Y方向前期隆起,后期沉降;从空间上看,变形集中在边坡的中下部区域及低风化岩层处。
3) 施工时间间隔对边坡变形和稳定性的影响较小;而有、无锚固结构对边坡变形和稳定性的影响显著,建议在保证施工安全的前提下尽量减小施工间隔,但针对高危岩质边坡,应加强对锚固结构的应用,开挖一级,锚固一级。

