基于极限分析法原理的浅埋隧道围岩受力监测对比分析

黄华鹏

(中铁十八局集团第一工程有限公司，河北 涿州 072750)

由于浅埋段软弱围岩自稳能力较差，在隧道开挖时受到扰动较显著，浅埋段发生延伸至地表塌陷灾害事故的可能性远高于深埋段[1-3]。围岩埋深较小时，隧道围岩塌落体将持续发生延伸至地表，且隧道所需支护力往往随埋深的增加而增大；埋深较大时，隧道围岩塌落范围较为稳定，埋深对其不再有明显影响。为了保证浅埋隧道开挖施工的安全性和隧道围岩稳定性，有必要对隧道围岩压力变化规律、顶部塌落范围及隧道浅埋段影响范围进行研究，为取得适当的围岩支护参数提供理论支持。现阶段，已有大量学者对深埋段隧道两种状况进行隧道围岩塌落问题的研究[4-12]。黄阜[13]从考虑隧道围岩支护力和锚杆支护效果角度出发，对深埋段隧道支护作用下的围岩塌落内部机理进行分析。这些研究有力地推动了深埋围岩破坏时的崩塌范围和隧道变形机理研究的发展，然而浅埋隧道与深埋隧道由于地层特性不同，因而在围岩塌落机理上存在较大的差异，且考虑到浅埋段隧道具有随埋深以及地形变化而有较大变化的特性，不能简单地定性为浅埋隧道或深埋隧道，两者界限并不明确；构建隧道顶部恰当的塌落区是分析隧道稳定性及围岩压力的前提条件，由此探究不同埋深条件下隧道围岩压力分布关系显得十分必要。本文在Hoek-Brown破坏准则的基础上，分析了浅埋段隧道坍塌上限解，并基于隧道围岩压力沿隧道轴向变化规律确定隧道浅埋段的范围，通过实际工程验证公式的适用性，为类似工程提供借鉴。

1 工程概况

1.1 工程简介

新建云桂铁路云南段(小坡头隧道六标工程)工程，位于弥勒—石林板桥区间，双线隧道，隧区属构造剥蚀滇东南低中山剥蚀丘陵地貌，地形起伏小，地面高程1523～1467m，相对高差约40m；地面横坡陡峻，自然坡度10°～25°，坡面植被较发育。监测段隧道出口为小坡头村，有便道通向隧道进出口及洞身附近，交通较为便利。全隧道均位于曲线半径为5000m(左线)的右偏曲线上，线路设计为17.3‰单面上坡，本隧进口位于DK637+180，出口位于DK637+755，中心里程DK637+467.5，全长575m。隧道最大埋深约46m。

1.2 工程地质

2 浅埋隧道围岩顶部塌陷面上限分析

2.1 浅埋段坍落面方程推导

在山岭隧道掘进过程中如围岩支护不及时，极易出现“冒顶”的灾害事故，隧道顶部塌落体(见图1)在隧道埋深较小时，将持续延伸至地表，假设塌落体顶部宽度与底部宽度分别为L1、L0，在均质岩石或岩土体中，坍塌落体具有左右对称的规律表现。稳定岩体与塌落体被塑性临界面隔离开，可将其视为塑性理论中的速度渐变断面。为了不受人为假定的主观因素带来的脱离工程实际的影响，不对塌落体外观形状进行预先假设。设定塌落面由函数f(x)表达，在主动极限条件下，隧道塌落范围内岩体塌落方向向下，其速度为u，沿速度断面f(x)的岩体发生分离，分界面上作用有岩体破坏时的剪切应力τ和法向应力σn，因此，本文对Hoek-Brown破坏准则采用莫尔平面上的表达形式[14-15]：

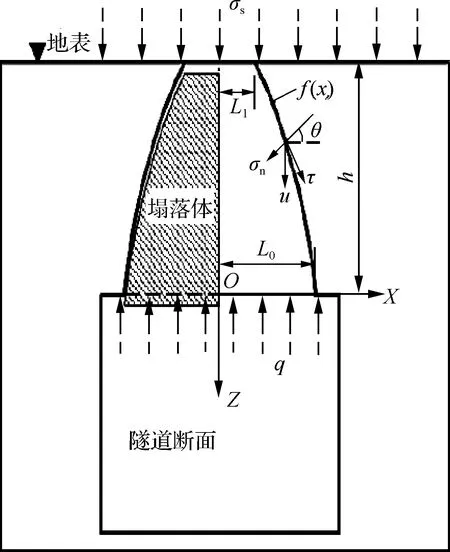
图1 浅埋隧道塌落

(1)

式中σc——岩体的单轴抗压强度；

σt——岩体的单轴抗拉强度,MPa；

A、B——三轴试验所得无量纲常数。

隧道岩体材料与流动法则相关联时，屈服面与塑性面为一共同体，因此，塑性函数可表示为

(2)

屈服面剪切应变γ与正应变ε可表示为

(3)

基于极限分析的上限分析定理，可得隧道岩体坍落面上任意点处的耗散功率Di

(4)

耗散能可表示为

(5)

重力所做的功为

(6)

式中h——隧道埋深；

γ——围岩上部土体重度，kN/m3。

地面因超载所做功为

Pσs=σsL1u

(7)

隧道围岩支护力q的功率可表示为

Pq=quL0cosπ

(8)

根据虚功原理[16]，将外力做功与总内能耗散之差定义为待求解的目标函数，可表示为

(9)

其中，函数Λ[f(x),f′(x)，x]为

Λ[f(x),f′(x)，x]=σt-σc[ABf′(x)]1/(1-B)

(1-B-1)+γf(x)

(10)

采用变分法原理对式(10)进行求解，得到其相应的欧拉方程为

(11)

对式(11)进行化简可得

(12)

进一步计算其通解为

(13)

将式(13)分别代入式(10)和式(9)，可得

+C1γ

(14)

(15)

考虑边界条件，地表位置剪切应力为0，即

τxy(x=L1，y=0)=0

(16)

求解可得

C0=γL1

(17)

在隧道塌落面的两个端点位置边界条件为

(18)

联立求解，可得

(19)

由能量守恒定理，外力所做功与塌落面上消耗率相等，对式(9)进行化简，可得

(20)

可解得塌落面方程为

(21)

2.2 隧道围岩压力理论计算

令L0=b，b为浅埋隧道截面宽度的1/2，对变分公式进行优化，可通过上限解析法对隧道围岩压力进行解析，所得表达式为

(22)

式(22)中，h为变量，沿浅埋段隧道纵向埋深产生变化。

结合隧道浅埋段地表单一方向倾斜(见图2)，可假定

图2 浅埋段隧道围岩压力

h=Ltanα

(23)

将式(23)代入式(22)，计算得到隧道围岩压力为

(24)

2.3 各参数对浅埋偏压隧道围岩压力的影响

首先分析边墙侧压力系数k和底部支护力系数u对围岩压力的影响。参考已有相关文献，u取0.8、1.0、1.2，k取0.6、0.8、1.0、1.2、1.4进行计算。浅埋偏压隧道的围岩压力计算的结果如图3(a)所示。由图3(a)可知，当隧道其他参数确定时，偏压隧道的极限围岩压力随k与u的增大而显著减小，随着k值的增大，对于浅埋侧和深埋侧的围岩压力差距也在逐渐减小，且系数k对深埋侧的影响大于浅埋侧。即浅埋偏压隧道的稳定性随着隧道两侧和底部支护结构功率增大而提高。这也符合工程实践中适当合理地加强隧道两侧和底部支护，进而可减小维持顶部稳定所需要的支护力，提高隧道整体稳定性的实际情况。在隧洞开挖后，受到影响的围岩和土体应是一个包含隧道顶部、两侧和底部的整体，在进行隧道稳定性问题研究时，不应忽略底部支护作用，只考虑隧道两侧和顶部支护力。

保持其余参数不变，u、k取为1.0。变化强度参数取值，黏聚力取5MPa、10MPa、15kPa，内摩擦角取10°～20°进行计算。从浅埋偏压隧道的围岩压力计算结果[图3(b)]中可以得到，随着围岩黏聚力、内摩擦角的增大，深埋侧和浅埋侧围岩压力都呈显著减小趋势。这说明，增强岩土的抗剪强度，隧道破坏时所需内耗能也相应增加，维持围岩稳定性所需的极限围岩压力也随之降低，进而隧道稳定性得以提升。因此，在工程实践中，可通过施工工艺，如错杆、预注浆等措施来提高围岩强度参数，进而提高隧道围岩稳定性。

图3 参数对围岩压的影响

3 理论计算与现场监测对比研究

以小坡头隧道工程为例，将实测浅埋段围岩压力与本文计算值进行对比(见图4)。隧道采用双侧隔壁导坑法施工，隧道开挖面高8.09m、宽12.485m，隧道洞口高程为530m，隧道轴向线路最大坡度为5.2%，隧道采用钢拱架初期喷混和二次衬砌的方式进行支护，试验测试的压力盒安置于钢拱架外侧，与围岩紧密粘贴。初期喷混厚度为25cm，二次模筑厚度为42cm，仰拱厚度设置为65cm，开挖轮廓到二次衬砌横面见图4，由于沿隧道轴线方向地势起伏变化较为平缓，可将隧道浅埋段假定为单项倾斜，倾斜18°。隧道轮廓由多心圆构成，隧道拱顶位置处圆弧最大，为了计算方便，将隧道上方围岩设置为水平，取隧道宽度的一半作为横断面的半宽(b=6.3m)，围岩岩体的平均重度为19.2kN/m3。隧道围岩力学参数：内摩擦角(φ)为26°，黏聚力(c)为12.3kPa。令Hoek-Brown破坏准则中参数B=1，所得相应计算参数等效方法如下：

图4 隧道剖面

τ=-σtA+Aσn=c0+σntanφ

(29)

经计算得：σt=0.026MPa，A=0.49。

采用高精度振弦双模压力盒(YT-200A)对隧道围岩压力进行监测，压力盒分辨率大于0.05%F.S，其有效测量压力范围为0～2MPa。监测点在隧道断面的左右拱脚分别设置一个、左右拱肩均设置一个及拱顶处设置一个。监测范围为隧道口向内60m，由隧道口起始断面开始向内每5m设置一个监测断面，共设有12个。根据图4监测布置方式，得到随洞口向内延伸土压力的变化关系(见图5)。

施工时，随着开挖施工以及临时构筑物的拆除，测得围岩压力总体表现为渐渐增大，随后逐渐趋于稳定。本文研究选取测试所得围岩压力趋于稳定后的最大值。由图5隧道浅埋段围岩压力对比曲线可知，围岩压力随着隧道埋深的增大呈现出逐渐增大的趋势。经本文公式理论计算所得的围岩压力值与实测值变化规律相似，其值略大于实测值，预测结果偏安全。根据实测结果，试验截面与隧道洞口距离超过30m时，围岩压力达到其峰值，上覆盖土厚度对其影响明显减小，围岩压力趋于稳定，该规律与公式计算结果基本吻合，表明新建公式对本工程具有良好的适用性。

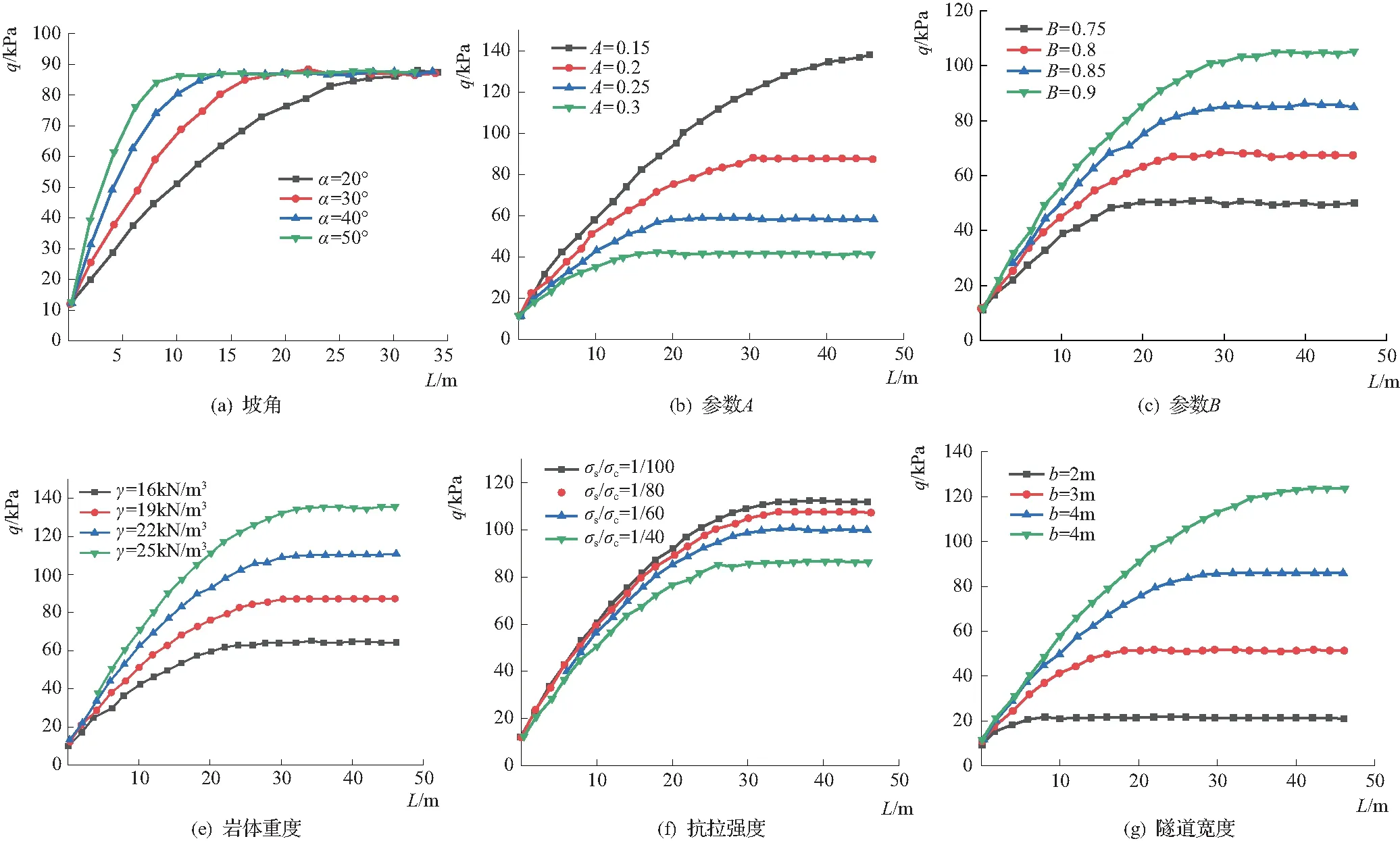
图5 隧道浅埋段围岩压力

4 结 语

本文结合隧道上方覆盖层塌落体围岩自承能力及形成机理，基于塑性理论对隧道浅埋段围岩压力进行分析，所得结论如下：覆土厚度和围岩力学参数是塌落面形状主要影响因素，坡角对隧道围岩压力峰值影响较小，但其增大时会使得隧道浅埋段范围内的土体压力增大，使隧道围岩压力达到峰值时间点有所提前；浅埋偏压隧道的稳定性随着隧道两侧和底部支护结构功率增大而提高，随着围岩黏聚力、内摩擦角的增大，深埋侧和浅埋侧围岩压力都呈显著减小趋势；对实际工程进行的监测结果表明，围岩压力达到其峰值，上覆盖土厚度对其影响明显减小，围岩压力趋于稳定，该规律与理论计算结果基本吻合。