一种炸弹投放通用控制策略的研究与实现

梁凯，李伟

1.洛阳电光设备研究所

2.空装驻洛阳地区第二军事代表室

国内攻击型飞行器机载非制导炸弹拥有多种挂载构型，控制逻辑复杂。为满足实战环境下的炸弹安全和精准投放要求，本文分析当前典型攻击型飞行器机载炸弹的挂载构型，建立数学控制模型，设计并实现了多约束条件下的安全投放控制策略。通过仿真验证，炸弹投放控制策略有效规避了炸弹投放过程中的安全风险，提高了炸弹投放控制管理效率，对攻击型飞行器机载武器管理系统的智能化发展具有重要意义。

炸弹作为一种常规非制导空地武器，具有杀伤力大，覆盖面广，抗干扰能力强，操作简单且成本较低的特点，成为多种攻击型飞行器的标准配装武器，广泛应用于各种空地作战。

影响因素分析

随着先进制造技术和前沿科学技术的不断进步，攻击型飞行器与机载武器的性能取得了质的提升，各种小型多功能炸弹不断升级迭代，增强了各类攻击型飞行器的打击能力。但是，原有炸弹的投放控制策略变得越来越不适应实战应用，主要表现在以下三个方面。

（1）多枚弹投放时可能出现弹体干涉。

（2）炸弹投放出现异常情况时，攻击型飞行器的重心会不平衡。

（3）炸弹挂载数量多，导致其投放控制复杂且执行效率低。

为解决上述问题，本文研究一种炸弹通用投放控制策略，以满足当前各类攻击型飞行器挂载炸弹，执行多元化作战任务的要求，提高炸弹投放可靠性及任务完成效率，降低炸弹投放安全风险和机载武器控制系统维护成本。

不同类型炸弹在攻击型飞行器上的挂载位置分布截然不同，导致其投放控制逻辑也不尽相同。通常，攻击型飞行器的武器初始挂载状态采用对称分布形式，即在对称挂点安装相同的挂架，用来挂载相同类型和数量的炸弹。对称分布可以确保攻击型飞行器在给定的初始状态下，能够按既定计划执行任务，满足最大目标期望。但是，炸弹投放过程存在挂载位置布局的变化，由此增加了投放安全风险，加剧机体重量不平衡，增加了炸弹投放控制逻辑的难度。因此，炸弹投放控制过程要解决以下三方面问题。

图1 多弹投放产生弹体干涉的示意图。

弹体干涉

当攻击飞行器的某个单挂点挂载多枚炸弹时，在一定程度上会压缩该挂点与相邻挂点间的空间距离。在攻击型飞行器执行任务过程中，若炸弹采用齐投方式，即相邻挂点的两枚或多枚距离较近的炸弹同时投放（如图1所示），可能产生弹体间的空中相互干涉，这种干涉一旦出现，就会危及攻击型飞行器的安全。

配平安全

在执行任务过程中，存在炸弹投放、燃料消耗和任务变更等各种阻断当前计划执行的因素，使得攻击型飞行器挂载布局逐步向非对称分布发展，并导致攻击型飞行器的重心趋于不平衡状态。这时须要机载武器控制系统对炸弹投放控制策略进行自适应调整，根据新的分布状态及其他约束条件，自动调整控制逻辑，保证攻击型飞行器在执行任务过程中不超出重心包线，保持机体重量平衡，提高攻击型飞行器的操纵稳定性。

投放控制复杂

攻击型飞行器的武器挂载能力不断增强，并借助于各种异构形式的挂架，使可挂载炸弹的数量快速增多。攻击型飞行器可挂载的炸弹数量增多，导致炸弹投放控制变得越来越复杂且执行效率低。炸弹投放控制逻辑复杂会降低炸弹投放的可靠性和安全性，增加了过程中的不可控因素。

根据上述三方面影响因素的详细分析，现确定炸弹投放控制策略的限制条件。

投放限制条件制订

攻击飞行器根据自身特性、设计要求和原则，制订挂点优先级顺序以及所采用的挂架挂位的优先级顺序，并分析相应的炸弹投放限制条件。在攻击型飞行器涉及的炸弹投放规则中，大部分规则具有相同性，主要差异表现在挂载能力、挂载方式以及适配的运载悬挂物。通过对典型攻击型飞行器的规定性限制条件进行分析、提取、简化，得到三个主要投放限制条件。

（1）挂点的优先级顺序。

（2）挂架挂位的优先级顺序。

（3）挂点及挂架挂位间的干涉位置。

任务执行条件制订

针对目标特性，应考虑攻击型飞行器所使用炸弹的类型，以及环境对炸弹投放产生的影响等因素。影响因素被确定后，攻击型飞行器在执行目标任务时，须要多个系统共同参与并相互协作运行。为隔离系统间协作产生的影响，任务执行条件中忽略系统间的协作运行要求和各独立系统参与的重要性等条件，重点阐述攻击型飞行器机载武器控制系统中在整个任务环节中所须要考虑的条件。

当攻击型飞行器中的其他系统处于理想工作状态时，机载武器控制系统进行武器投放须要满足下列基本条件。

（1）识别出可用于执行任务的武器。

（2）满足武器优先级使用要求。

（3）武器投放系统处于可投放状态。

安全条件制订

在执行任务过程中，根据安全性要求以及机载武器控制系统的控制范围，对可能影响攻击型飞行器安全与人员安全的因素进行合理和规范化处理。

（1）重量平衡

根据攻击型飞行器的配挂限制、任务规划、炸弹挂载数量和规格，炸弹应对称分布在机翼两侧，以防止攻击型飞行器重心偏移，超出重心包线。

在炸弹实际投放过程中，攻击型飞行器机翼及机身的重量在不断变化，会使机体两侧产生扭矩偏差，导致攻击型飞行器重心不断偏移。因此，炸弹投放后必须尽量保证机体重量的平衡，避免影响攻击型飞行器的飞行稳定性。

基于上述原因，在炸弹投放过程中，为保证机体重量平衡和重心偏差在设计范围内，在假设攻击型飞行器燃料为均匀消耗的基础上，仅考虑对机翼两侧任务载荷的重量偏差进行控制，以实现投放控制逻辑的条件限定。

（2）投放安全

炸弹投放安全须从分时投放和弹体位置两方面进行阐述。

①分时投放

分时投放是指，攻击型飞行器在投放多枚炸弹时，为避免弹道相同而发生弹体碰撞，须采用分时处理，炸弹分时投放过程一般采用时间间隔法。该方法是根据攻击型飞行器挂点分布、挂点使用的挂架、挂载炸弹的特性以及炸弹投放方式等因素来确定采用的时间间隔。分时投放可以确保连续投弹的时间分配合理有效。

②弹体位置

弹体位置是指炸弹处于攻击型飞行器各挂点或各挂架挂位的具体挂载位置。确定当前待投放炸弹的位置分布，通常以当前弹体位置分布为基础，并根据安全原则，规避投放时存在空间重叠危险的弹体位置。例如，当相邻位置存在多枚炸弹时，应设置规则，避免相距最近的炸弹同时投放，确保投放时炸弹受到该规则约束。

理论模型

模型假设

算法策略仅考虑常规挂载模式下的任务过程并简化理论模型，依据本文分析的影响因素建立相应的数学模型。

假设Pn型攻击型飞行器的炸弹挂点集合合S={s1,s2,···,sn}，(n≤N)，，其中n为可挂载炸弹的挂点数量，N为Pn型攻击型飞行器最大挂点数量。假设该型攻击型飞行器能够挂载x，y，z三种类型炸弹，该型飞行器挂载的x，y，z三型炸弹的数量分别为Bx，By，Bz。另外，Pn型攻击型飞行器对某一种类型炸弹的最大挂载数量有限制，采用Qimax表示i型炸弹在该型飞行器上的最大挂载数量，即有Bx≤Qxmax，By≤Qymax，Bz≤Qzmax。根据任务特性和Pn型攻击型飞行器挂载构型要求，Pn型攻击型飞行器挂载多种类型炸弹时须满足以下四个条件。

（1）同类型炸弹必须对称挂载在攻击型飞行器上，且保证挂架类型一致。

（2）不论采用何种挂架类型，单个挂点只能挂载同类型炸弹。

（3）单个挂点挂载的炸弹数量不能超过该飞行器规定的该型炸弹最大挂载数量。

（4）攻击型飞行器挂点的优先级顺序Ps与挂架挂位的优先级顺序Ph已知。

假定挂架类型分为两联挂架H2、三联挂架H3、四联挂架H4、六联挂架H6。如果攻击型飞行器挂点下不存在多联挂架，则默认为单点挂载。单点挂载的优先级顺序实际为攻击型飞行器挂点优先级顺序。

根据挂架结构，上述各类挂架投放的优先级顺序满足如下要求。

（1）后端先于前端投放。

（2）中部先于左侧投放。

（3）左侧先于右侧投放。

因此，可得出各类型挂架一般优先级排序Ph(j),j为挂架类型且满足(j=2,3,4,6)。即可得，

模型建立

设计人员综合考虑攻击型飞行器的作战用途和性能指标后，从已有炸弹类型中选择并确定每个挂点可挂载的炸弹类型。那么，已知Pn型攻击型飞行器各挂点可挂载炸弹类型和数量的配挂信息表g(i,S)，其中，i表示炸弹类型，S为挂点集合。为i型炸弹在Pn型攻击型飞行器各挂点配挂弹量的集合，则各类型炸弹满足挂载要求有如下情况。

（1）x型炸弹，满足各挂点配挂弹量

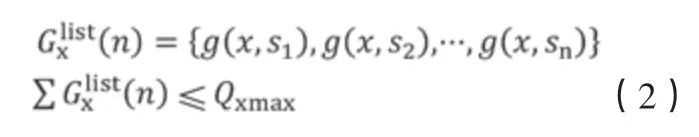
（2）y型炸弹，满足各挂点配挂弹量

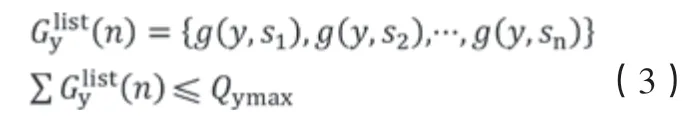
（3）z型炸弹，满足各挂点配挂弹量

在实际应用场景下，攻击型飞行器须要依据任务目标以及当前可使用的炸弹类型来规划炸弹投放控制逻辑。假设具有k个挂点的攻击型飞行器为Pk型，可挂载炸弹挂点集合为Sk= {s1,s2,…sk},(k≤M)，M为Pk型 攻击型飞行器的最大挂点数量。在某次任务中，Pk型攻击型飞行器须要配挂x，y，z三型炸弹数量的集合{Bx，By，Bz}，根据Pk型攻击型飞行器配挂信息表g(b, Sk)。那 么，由 式（2）（3）（4）计算并合并同类项可得到该型攻击型飞行器当前挂载三型炸弹数量的分配集合

再计算Pk型攻击型飞行器机体两侧炸弹挂载分配情况，分别由代表左右两侧挂点炸弹数量集合。则有：

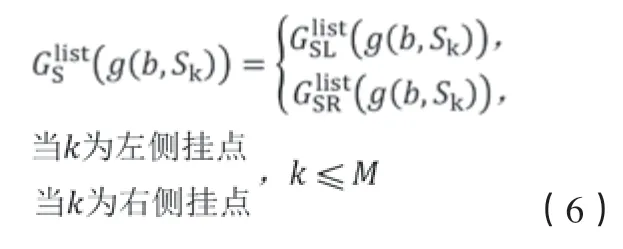
同时，已知x，y，z三型炸弹的质量大小集合为Q={Qx,Qy,Qz}，则机体重量平衡要求可表示为：

在机体挂载重量平衡要求的重量偏差基础上，结合攻击型飞行器挂点优先级顺序、挂架优先级顺序、炸弹优先级以及投放时间间隔等约束条件，参考背包算法原理，可计算出当前炸弹优先投放序列，其控制策略目标函数如下所示。

其中，q为本次须投放炸弹数量；w为要求的重量偏差；t为投放间隔时间；攻击型飞行器挂点优先级顺序Ps为已知约束条件；挂架优先级顺序Ph为已知约束条件；炸弹优先级Pb是根据任务规划和炸弹特性得出的炸弹选择优先级。

此外，结合作战实践，若出现炸弹挂载构型导致攻击型飞行器重量平衡偏差超出要求的特殊情况，则须从策略层面考虑采用以下两种方式处理这种情况，以实时动态地完成机体重量重心包线回归。

（1）重新调整炸弹优先级

按照使用等级，形成次优级、高级、中级、不可用等类别序列，进行降级使用。

（2）重新评估重量平衡偏差的范围

在攻击型飞行器重量重心和操纵系统允许的情况下，通过计算重量平衡偏差的方差，

判断与LimVal的离散趋势，并根据趋势判定LimVal的调整范围。

算法设计

依据上文给出的算法模型，利用伪代码进行算法描述。

已知算法输入条件如下。

（1）外挂物清单矩阵L

（2）挂点优先级序列Ps

（3）挂架优先级序列Ph

（4）炸弹优先级Pb

（5）投放数量m

（6）投放时间间隔t

（7）重量偏差阈值w

输出结果为炸弹最优投放序列，可根据实际须要进行定义。该算法伪代码采用队列结构描述HitQ，表示当前计算出的最优投放序列。算法伪代码如图2所示。

效率分析与应用仿真

复杂度

对上述实现策略算法进行测试与分析后可知，该算法执行效率主要由所要查找的炸弹数量及炸弹在攻击型飞行器挂点挂架位置分布决定。假设挂载z型炸弹Bz枚，Bz≤Qzmax，Qzmax为该 型炸弹的最大可挂载数量，依据配挂和选择规则，可得出最大的查找次数公式：

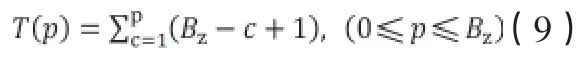
其中，p表示当前选择的炸弹数量，T(p)表示选择p个炸弹数所须要的最大查找次数。

可以将公式（9）进行变换，即：

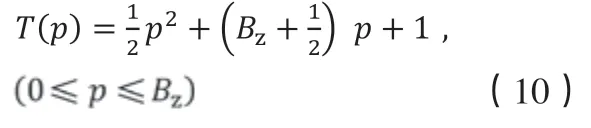
由变换后的公式（10）可以看出，该算法最大时间复杂度为O(Bz2)，最小时间复杂度为O(Bz)。

仿真验证

在综合试验平台上，试验人员通过配置实验数据，模拟了9个挂点挂载3种类型、共27枚炸弹的攻击型飞行器，并验证其中某型炸弹在算法执行后的投放顺序。

第一次，人工选择7枚炸弹作为投放数量。所选炸弹的数量及投放顺序标号详见图3（a），挂点下标出了占位框的位置。

图2 炸弹投放动态控制算法伪代码。

图3 动态选择炸弹投放策略的仿真界面。

第二次，人工选择6枚炸弹作为投放数量。从第一次人工选择后的剩余挂载炸弹中选取本次所选炸弹的数量及投放顺序标号，模拟器画面显示了投放顺序标号，详见图3（b）。

通过验证，该算法满足在保持机体重量平衡，不选择处于未准备好或故障状态的炸弹，同时保证同一挂点的挂架相邻挂位不能同时被选择等策略运用，实现了飞行器在不同重量重心、炸弹类型及预设优先级顺序等约束条件下，动态地选择炸弹投放。

总结

攻击型飞行器执行任务时，炸弹的投放精度越高，离机环境越安全，大幅提高了飞行器的攻击效率和战场生存率。本文采用数学建模方式，设计一种适用于攻击型飞行器机载炸弹投放的控制算法，可有效保障机载设备的任务完成率，降低武器使用过程中的风险。另外，在研究过程中，仅针对外挂点挂载场景进行分析和验证，研究人员未考虑内埋弹舱挂载情况，后续将优化算法，不仅考虑内埋弹舱的挂载情况，也会针对新型炸弹的挂载、任务交叉、复杂环境等方面，开展协同作战环境下的投放策略研究，逐步实现炸弹智能化精准投放和控制能力。

美国海军陆战队采购2架MQ-9A“死神”无人机

美国通用原子航空系统公司于2021年10月15日 将2架 第5批 次MQ-9A“死神”无人机、两套地面控制站和相关支持设备交付美国海军陆战队。根据通用原子航空系统公司与海军航空系统司令部之间的租赁协议，这2架无人机自2018年以来，已经累计飞行12000飞行小时，一直由美国海军陆战队使用，支援该部队的紧急作战行动以及美军在中东的作战行动，同时开展了海军陆战队空地特遣队无人机远征项目测试。