电压驻波比测量不确定度的评定和表述

高申翔， 夏 伟， 顾卫红， 柏永斌

(中国卫星海上测控部，江苏 江阴 214431)

1 引 言

电压驻波比(voltage standing wave ratio,VSWR,简称驻波比)是表征射频/微波器件反射特性的传统参量[1]，现在仍有应用场景。比如很多厂家仍用驻波比作为仪器输入/输出端口的反射特性技术指标；用来校准网络分析仪的标准失配器仍用驻波比标称其量值。表1是几个大型实验室在CNAS网站上公布的驻波比测量能力。

对表1测量不确定度的质疑：1)小信号的测量不确定度应该大于大信号的测量不确定度，整个测量范围的不确定度不应该用一个数值表示；2)给出的不确定度对于某个范围的测量值是否偏小？

本文将针对以上问题开展研究，并给出表述驻波比测量不确定度的建议。

表1 部分实验室公布的驻波比测量能力Tab.1 Measurement capability for SWR of some famous laboratories

表2为当前某主流型号网络分析仪电压反射系数ρ的测量不确定度,表中MPE为最大误差。显然，反射系数越小，不确定度越大。

表2 ZVA24型网络分析仪反射系数模值测量不确定度(50 MHz～24 GHz)Tab.2 Measurement uncertainty of reflection coefficient’s amplitude at frequency 50 MHz to 24 GHz of ZVA24

2 SWR测量不确定度的GUM法评定

现在几乎所有实验室都用矢量网络分析仪测量驻波比，然而，产品手册一般只给出电压反射系数的测量不确定度，它们之间的关系为

(1)

式中：S是电压驻波比；ρ是电压反射系数模值。

根据不确定度传播律[2～4]，用GUM法可以从ρ的不确定度计算出S的不确定度。但是，式(1)明显为非线性函数，函数图形如图1所示。用幂级数将式(1)展开[5]

S=(1+ρ)(1+ρ+ρ2+…)

=1+2ρ+2ρ2+2ρ3+…

(2)

图1 公式(1)函数图形Fig.1 Curve of equation(1)

对于式(2)，一阶近似不确定度传播律为

u(S)=2u(ρ)

(3)

三阶近似不确定度传播律为

(4)

式中:u(S)、u(ρ)分别为S和ρ的标准不确定度；S′、S″、S‴分别为S的一阶到三阶导数。

3 公式(4)的推导

引理根据文献[6]，若X服从标准正态分布，即x～N(0,1)，则E(X2)=1，E(X3)=1，于是

(5)

证毕。

4 驻波比不确定度的蒙特卡洛法评定

为了比较公式(3)和公式(4)计算结果的误差，本文以蒙特卡洛法评定[7～9]的驻比标准不确定度为参考值。蒙特卡洛法的基本算法为：

1) 假设ρ服从正态分布，这是公式(4)成立的前提；

2)ρ的数学期望ρ0和标准偏差δρ的水平根据表2设置，其中σρ=ρ0·MPE/3；

3) 用Excel内置函数NormInv产生ρ的正态样本，代入式(1)产生S的样本；

4) 用Excel内置函数Stdev计算S的标准偏差。

具体算法见文献[10]，仿真结果见图2、图3和表3所示。

图2 ρ服从正态分布时S的概率密度曲线Fig.2 Probability density curve of SWR when ρ obeys normal distribution

图3 ρ服从均匀分布时S的概率密度曲线Fig.3 Probability density curve of SWR when ρ obeys uniform distribution

4.1 仿真结论

由表3可以看出，当驻波比大于1.4时，公式(3)的估算误差已超过30%。对于公式(4)，当驻波比不大于2时，估算误差不超过11%；但是当驻波比大于3时，估算误差将超过30%。

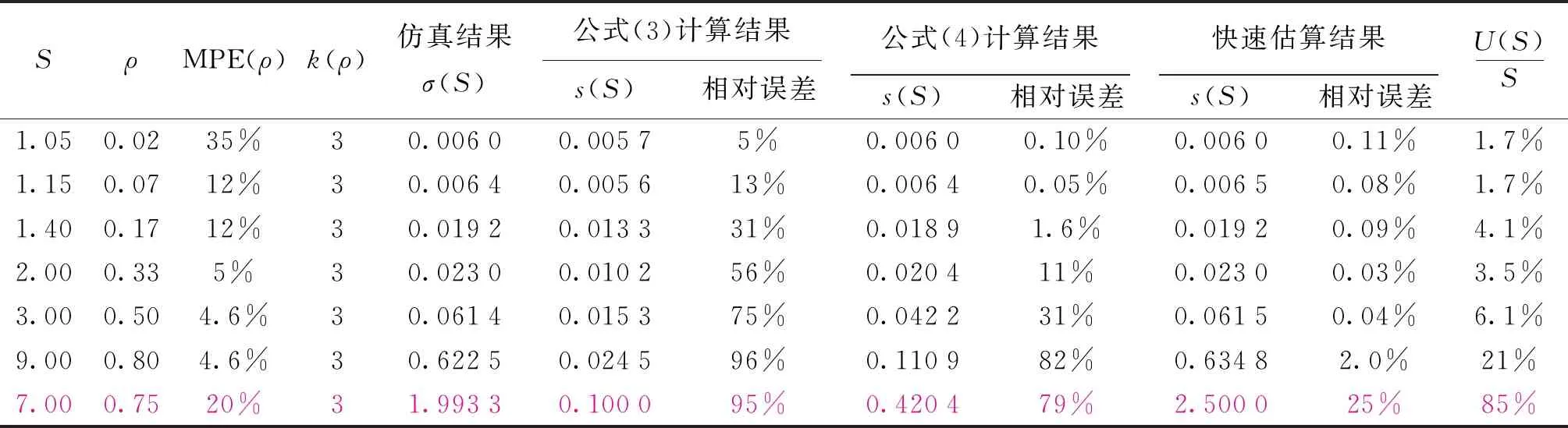
表3 蒙特卡洛法仿真结果(ρ服从正态分布)Tab.3 Simulation results of MCM when ρ obeys normal distribution

由图2和图3可以看出：在假定ρ服从正态分布或均匀分布的前提下，S与ρ具有相同的分布。由此可以得到一种快速估算S标准不确定度的方法：

1) 根据ρ的最佳估计值及其最大测量误差(或扩展不确定度)，利用公式(1)计算S的分布区间，进而得到其分布区间半宽度a(S)；

2) 假设k(ρ)是ρ的标准不确定度的包含因子(如表3列4)，则S的标准不确定度为

u(S)=a(S)/k(ρ)

这里不打算定量检验S的分布类型，对于工程计算来说，关心的是估算结果的误差是多大[11]。由表3倒数第2列可以看出，即使ρ=0.8，估算误差不超过2%(不含最后一行)。

4.2 快速估算法的数学基础及推广

由图1可以看出，当ρ趋近0时，曲线近似为直线；当ρ趋近1时，曲线的非线性增强，但是根据表2，此时ρ的测量误差变小，使得在ρ的变化区间内曲线可近似为直线。因此，在表2给定的条件下，图1在任何一个ρ的邻域内均可近似为直线；于是公式(2)的高阶项可以忽略，从而在整个测量范围内S与ρ同分布；进而该方法可以推广到满足下述条件的测量模型：

1) 输出量与输入量是一元函数关系；

2) 在输入量测量值的误差范围内，函数是单调的且近似为线性函数；

3) 经蒙特卡洛法验证，以上近似带来的标准不确定度估算误差是可以接受的。

表3最后一行是人为增大ρ的测量误差后的仿真结果，此时快速估算法的误差明显增大，达到25%。

5 驻波比测量不确定度的表述

表3最后一列给出了驻波比的相对测量不确定度，即扩展不确定度与测量值的比[12]。根据表2的参数水平，将表3的结果扩展到驻波比的常见测量范围，如图4所示。

图4 驻波比为1～5时的相对扩展不确定度Fig.4 Relative expanded uncertainty when SWR is 1 to 5

由图4可见:驻波比的不确定度随着反射系数不确定度的变化分为3段。因为测量值越大，图1的非线性越强，所以每个分段内，不确定度随测量值单调递增。对照图4和表1，可见目前一些实验室给出的不确定度当驻波比大于3时是偏小的。

本文建议，可以根据反射系数测量不确定度的分段，用相对扩展不确定度分段表述驻波比的不确定度，每段用最大值或“最小值-最大值”的形式表述。在简要表述场合(例如CNAS校准能力表),也可以用整个测量范围的“最小值-最大值”的形式表述，但是实验室应提供详细表述文本。

6 结 论

1) GUM法评定驻波比的不确定度误差较大，当驻波比大于1.4时，一阶近似的估算误差已超过30%；当驻波比大于3时，高阶近似的估算误差将超过30%。

2) 在常规测量条件下驻波比与反射系数同分布，因此,可通过估算驻波比分布区间快速计算其标准不确定度。在反射系数为0.5，相对扩展不确定度为4.6%时，驻波比不确定度的估算误差约为6%。

3) 驻波比的不确定度应该用相对扩展不确定度分段表述。