局部围线积分双谱的雷达信号源指纹识别技术
江西工业职业技术学院 龚再兰
在处理和分析非最小相位系统、非高斯过程和非线性系统的一种重要方法是双谱分析法,双谱的重要特征是高阶谱能够反映出其信号的相位信息,除了线性相位以外,双谱包含了全部的信号信息,且双谱分析法中雷达信号的双谱具有平移不变性,因此双谱分析法有效的应用在雷达信号源指纹特征提取中。虽然双谱在理论可以完全抑制任何对称分布的非高斯噪声和高斯噪声,但是直接应用双谱分析作为识别雷达信号源的特征向量,不仅有很大的信息冗余,而且还需要有足够大的目标模板库。
为了减少双谱的数据量,以达到减少目标模板库存储量和信息冗余以达到实时处理信息的目标,本文提出了局部围线积分双谱的辐射源个体识别的方法,即利用双谱分析双谱估计值中具有最强鉴别能力的部分双谱估计值,对辐射源个体特征参数进行提取、优化,作为辐射源分类识别的特征向量,并用重构核函数的支持向量机完成识别三部不同雷达信号源个体的信号。实验结果表明,该方法具有较高的识别率。
1 局部围线积分双谱及二次特征提取
1.1 局部围线积分
在区分M个雷达信号源时,每个雷达信号源发射信号可记为{N1,N2,...,NM},围线积分双谱定义式为:

式(1)中,i=1, 2,...,M为雷达信号源数目,v=1, 2,...,Ni为捕获的信号数据组数,Rl(l=1, 2,...,L)为围线双谱积分路线。鉴别函数表达式为:
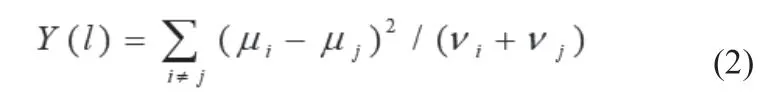
式(2)中,μi、μj为第i、j类信号积分双谱的平均值,vi、vj为信号的积分双谱的方差。局部围线积分双谱法,即在围线积分双谱中利用鉴别函数Y(l)来筛选出相对大的参数值,把筛选出来的参数值重新组合成一维矩阵数组。
1.2 二次特征值提取
在局部围线积分双谱重新组合成的一维矩阵数组的基础上提取特征值,因为双谱的奇异值具有稳定性、转置不变性和位移不变性,因此,在雷达信号源的信号识别过程中把双谱的奇异值作为识别和分类的特征向量。为了不遗漏或不丢失有用的奇异值信息,并且最大限度降低特征向量的维数,本文利用信息熵理论,二次特征提取双谱的奇异值熵、能量熵和波形熵。
2 重构核函数
本文在支持向量机解决两类分类问题的基础上,衍生出支持向量机一对多的设计理念,即进行有M类信号时,就需要M个判决函数。分类判决的优劣在于判决函数中核函数的选取,因为核函数的选择不同就会识别出不同的分类效果。为了解决提高分类识别率的问题,本文有机的融合了两种核函数的优点,采用了由多项式核函数和高斯径向核函数线性相关的重构核函数,重构核函数的设计理念找到最优的线性参数值,即筛选出最优核函数,其表达式可写为:
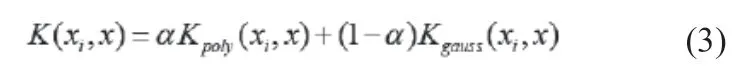
式(3)α∈(0, 1)。由实验经验值可知,Kpoly(xi,x)中的参数q和Kgauss(xi,x)中的参数δ,构成最优核函数的参数值为重构权重系数α = 0.98、q= 2和δ = 0.6。
3 分类器的设计
在分类器的设计过程中,可分为两个步骤:训练样本库和测试样本库。
第一步,训练王本库。针对M类雷达源信号分类器设计,本文采用逐次分类法的原理,即在训练第N类的分类器时,把属于第N类的训练样本记为I类,其余所有其他类的样本都标记为II类,根据重构核函数由支持向量机解出第N类的判决函数fN(xN, X),依次类推,直到训练出M个判决函数即M个分类器为止。对于每一类的类心,采用样本的质心代表,由支持向量机训练后得到的判决函数集为{f1(x1,x),f2(x2,x),...,fM(xM,x)}。
第二步,测试样本库。把测试样本x代入到各类已经训练完成的判决函数集,输出最大值的判决函数所对应的类别即为测试样本的所属类别。
4 实验数据分析及结果
实验分别采集由Agilent83752A信号源、Agilent E4438信号源和Anritsu MG3694B信号源发射的CW信号,并用Agilent型号为DSO6032A的示波器采集数据。CW信号的参数设置:载频分别为20MHz、40MHz、80MHz、100MHz、200MHz,采样频率为1GHz,每个载频采集六组实测数据,每组采样点数为1000个,重复周期为15μs,发射功率为6dBm,发射的脉冲宽度为1μs。为了能更突出地体现本文技术的优势,实验数据分别利用围线积分特征值提取及识别和局部围线积分特征值提取及识别进行对比。
4.1 围线积分特征值提取及识别
对所采集的数据的双谱值进行围线积分特征值提取,得到能量熵En,波形熵Eb,奇异值熵Es,利用重构核函数支持向量机,分类识别时以二维特征向量[Es,En]、[Es,Eb]、[Eb,En]识别参数。
图2和图3是载频为100MHz时利用围线积分法二维特征向量的识别结果。
表1为实载频分别为20MHz、40MHz、80MHz、100MHz、200MHz时,围线积分法进行分类识别率。由图1、图2、图3分类结果和表1可以看出,围线积分双谱法的分类识别率随着载频的增加而有所降低。
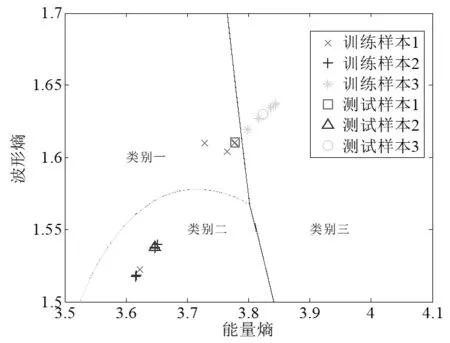
图1 En和Eb组成的二维特征向量的识别
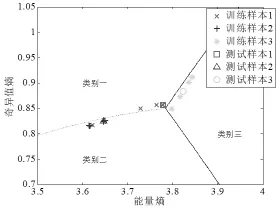
图2 En和Es组成的二维特征向量的识别

图3 Es和Eb组成的二维特征向量的识别
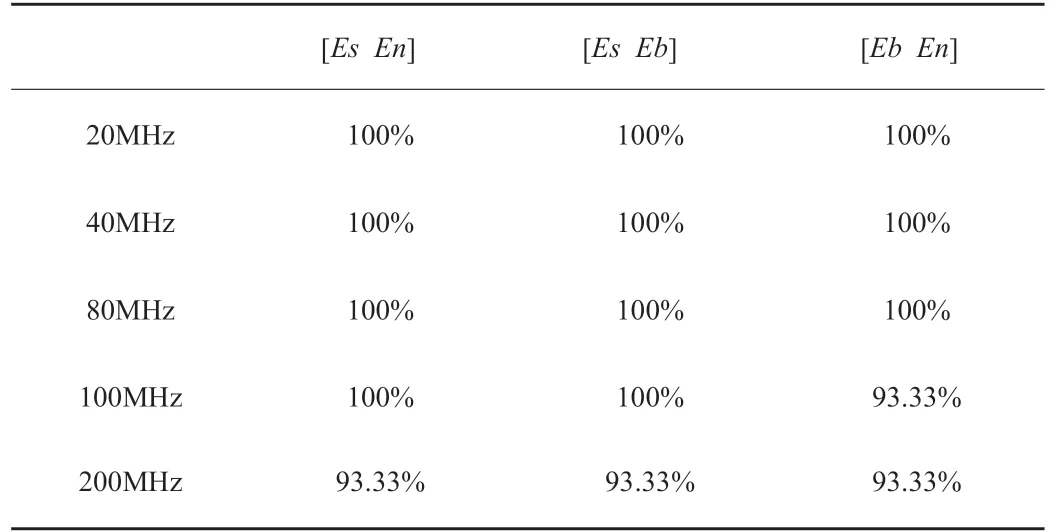
表1 围线积分法分类识别率汇总表
4.2 局部围线积分特征值提取及识别
局部围线积分在进行特征向量提取时,经鉴别函数计算,求解出围线积分双谱中鉴别能力最强的前40圈,为了进一步减少测试模板库存储量和信息冗余以达到实时准确处理信息的目的,且更加直观的看出鉴别能力最强的前40圈的圈数与能量熵、波形熵的关系,图4、图5画出了鉴别能力最强的前40圈的圈数与能量熵、波形熵的变化曲线图,其中S1、S2、S3分别代表三部雷达信号源信号的双谱。
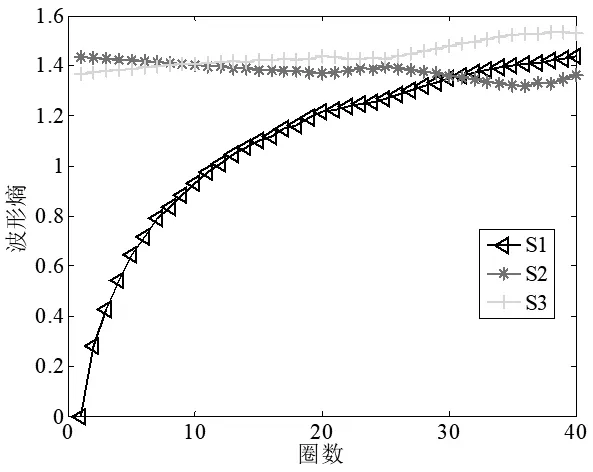
图4 波形熵与积分圈数的关系图
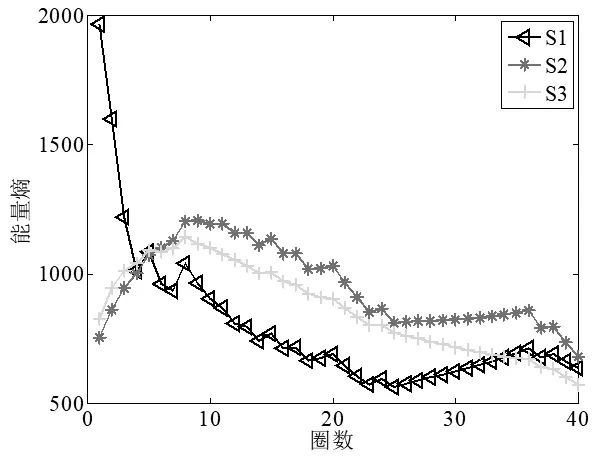
图5 能量熵与积分圈数的关系图
由图4、图5积分路径圈数与能量熵、波形熵的变化曲线可知,在利用能量熵、波形熵作为特征向量识别时,三部雷达信号源信号的双谱在局部围线积分中前18圈积分路径已具备了具有最优鉴别能力。因此,针对局部围线积分双谱中前18圈积分路径的波形熵和能量熵,与计算出奇异值熵两两组成二维特征向量,利用已经设计好的分类器进行分类识别,仿真图如图6、图7、图8所示。
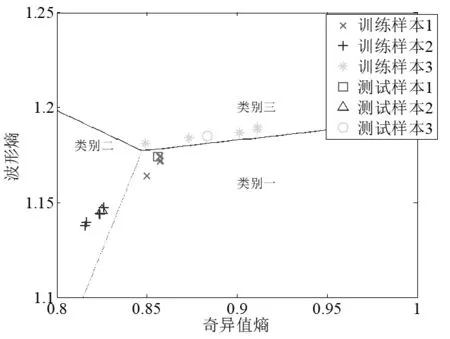
图6 Es和Eb二维特征向量的识别
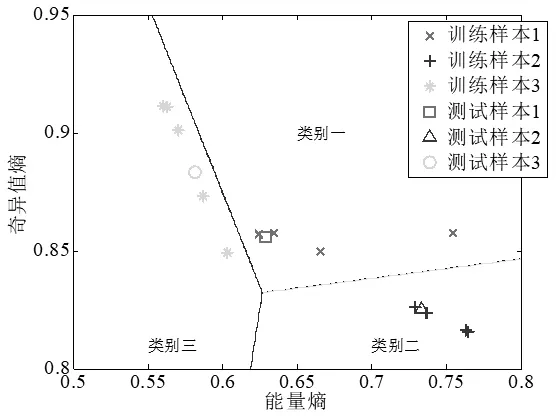
图7 En和Es二维特征向量的识别
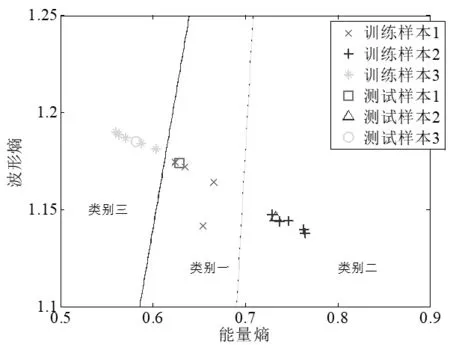
图8 En和Eb二维特征向量的识别
表2为实载频分别为20MHz、40MHz、80MHz、100MHz、200MHz时,局部围线积分法进行分类识别率。
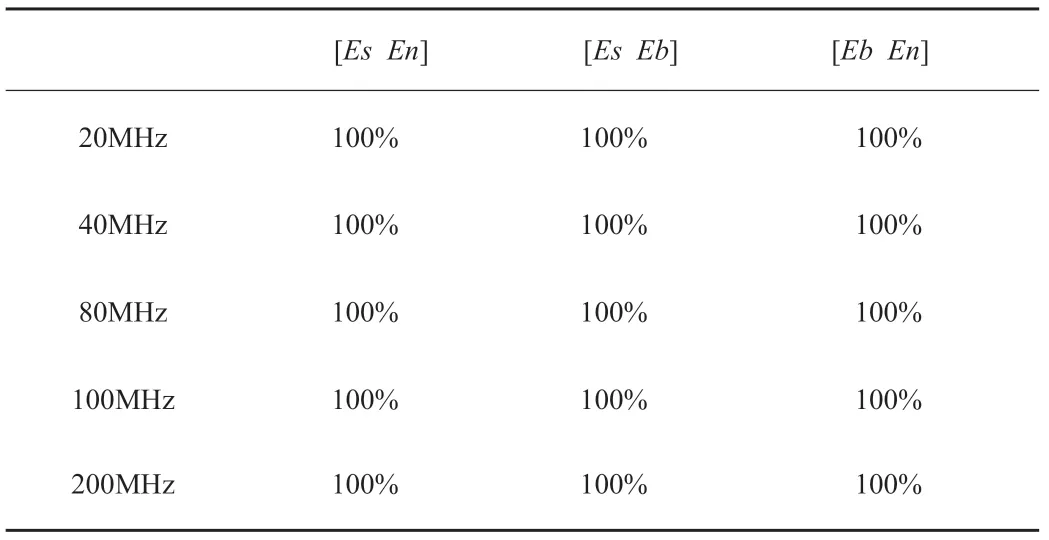
表2 局部围线积分的分类识别率汇总表
由图6、图7、图8和表2可知,局部围线积分法识别率随着载频的增加没有改变,提高了分类识别率。
本文根据围线积分双谱分析时存在目标模板库巨大存储量和信息冗余的缺陷,提出了局部围线积分双谱分析法,并进行二次特征值提取能量熵、波形熵和奇异值熵,构成雷达信号源分类识别的特征向量。通过实验数据分析可知,与直接的围线积分双谱分析雷达信号源的识别率进行对比,验证了局部围线积分的二次特征值提取有效地提高了分类识别率。

