一种适用于水声环境的变步长LMS算法
杭州应用声学研究所 罗 斌 张海生 王晓林
随着自适应信号处理在理论上的不断发展和实践应用,国内外研究学者从各方面着手,对自适应算法进行系统性研究。在自适应算法中,应用最为广泛的是Widrow等人提出的最小均方(LMS,Least Mean Square)算法,该算法具有成熟的理论基础、结构简单、稳定性好,易于工程实现,在水声信号处理中起着举足轻重的作用。
本文通过对LMS算法理论推导,分析算法性能影响因子,并提出一种适用于水声环境的变步长LMS算法,通过仿真对比,验证了该算法的性能。
1 LMS算法
1.1 算法原理
LMS算法原理框图如图1所示。
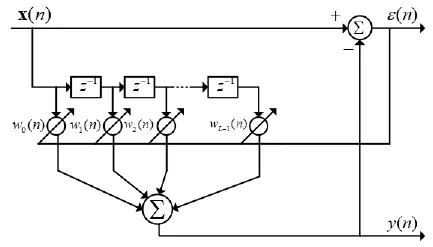
图1 LMS算法原理框图
图1中,输入信号矢量x(n)可表示为[x(n) x(n-1) … x(n-L+1)]T:L为滤波器阶数,T表示转置运算。
自适应滤波器的权矢量表示为[w0(n) w1(n) … wL-1(n)]T:则输出信号y(n)可表示为输入信号矢量与权矢量的乘积。
而自适应系统输出与期望信号的偏差则用ε(n)表示。根据LMS算法的思想,权系数更新表达式为:

式中,μ表示固定步长。
1.2 算法性能
研究LMS算法性能一般需综合衡量其收敛性、收敛速度、稳态误差及计算复杂度四项指标。研究表明,该四项指标可以用下面式子表示:
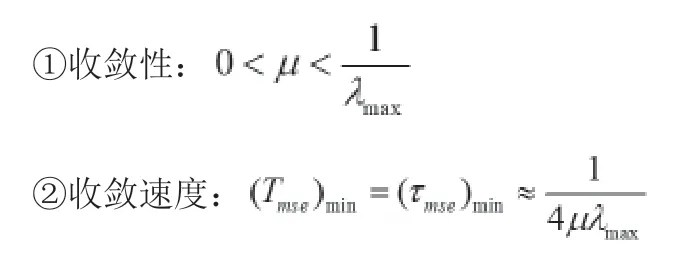

③中,tr[●]是迹运算,R表示输入数据自相关矩阵,对于自适应横向滤波器,该式亦可表示为:步长×滤波器阶数×输入功率。
结合收敛速度和稳态误差表示式可以看出,μ越大,算法可以获得较快的收敛速度,但同时也会带来较大的稳态误差;反之,μ越小,可以获得较小的稳态误差,但同时也会牺牲算法收敛速度。所以使用LMS算法时,要权衡收敛速度和稳态误差两者之间的关系,这对步长μ的选择提出了很高的要求。
2 变步长LMS算法
步长μ在LMS算法迭代过程中是一个矛盾量,它在控制LMS算法收敛速度的同时也决定了算法的稳态误差。因此,很多学者投入大量时间研究如何权衡两者之间的关系,提出了许多变步长LMS算法,这些算法的根本思想是在初始阶段选用较大的步长,使算法可获得较快的收敛速度,收敛到一定程度后逐渐减小步长,使算法最终能有较小的稳态误差。
在水声信号处理中,通常我们均假定噪声服从高斯分布,在较为理想情况下,噪声可看成为高斯白噪声。
在高斯白噪声背景下,噪声环境完全不相关,LMS算法步长可利用相邻时刻误差的互相关函数控制,能有效避免不相关噪声在步长迭代过程中的影响,因此上述算法能较好地适用于不相关噪声环境背景。但往往水声环境噪声不会这么理想,总会存在一定的相关性,如典型的高斯色噪声背景,在此种环境背景下,上述算法达不到预期效果。
下面引入一种适用于水声环境的变步长LMS算法,该算法步长利用误差的高阶函数控制,步长计算公式可表示为:步长与误差函数2阶和4阶指数函数相关。
上述算法步长利用了高斯信号的特性。只要噪声信号服从高斯分布,步长就不受噪声环境所干扰,从而使得步长迭代在高斯噪声环境下具有较强鲁棒性。实际的水声噪声环境通常均服从高斯分布,所以该方法具有较强的环境适应性和使用性。
3 仿真分析研究
下面通过权系数收敛曲线和输出误差曲线来比对分析第2章中所述的两种变步长LMS算法性能。
为方便说明,后续表述中用“算法一”代表利用相邻时刻误差的互相关函数表示的变步长LMS算法,用“算法二”代表利用误差的高阶函数表示的变步长LMS算法。图2、图3给出了仿真结果。

图2 高斯白噪声环境下算法性能对比
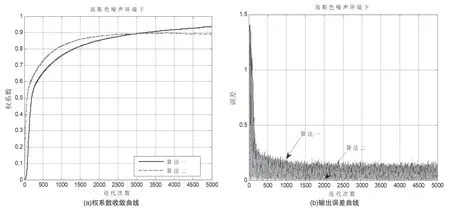
图3 高斯色噪声环境下算法性能对比
从图2和图3可见,在高斯白噪声环境下,由于噪声是不相关的,算法一性能较好,而当噪声环境为高斯色噪声时,由于噪声变得具有相关性,算法一性能大大降低,体现在收敛速度变慢,输出误差变大。但是算法二在上述两种环境下,均表现出较高的性能。
综上分析,本文提出的变步长LMS算法,能较好地适应于高斯噪声环境(即水声环境),可为水声信号处理提供良好的理论基础。
本文在分析LMS算法基础上,研究了变步长LMS算法理论,并在常规变步长LMS算法基础上,提出一种适用于水声环境的变步长LMS算法,该算法可在通常的水声环境下,很好地保证算法的收敛速度和稳态误差。仿真分析研究结果验证了该算法的正确性及有效性。

