辽河口生态环境监测浮标抗冰结构设计方案研究

吕奇鑫，许 宁，陈 元，袁 帅，张大勇，岳前进

(1.大连理工大学 运载工程与力学学部，辽宁 大连 116024；2.大连理工大学 海洋科学与技术学院，辽宁 盘锦 124221；3.国家海洋环境监测中心，辽宁 大连 116023)

海冰在我国北方海域属于一种特殊的生态环境因素，伴随着每年冬季的来临，海面都会经历长达3～4个月的冰期。我国最严重的冰情海域位于辽宁省南部沿海的辽河口与辽东湾地区，这两者也是“渤海综合治理攻坚战”的重点区域。海冰的生长与消融对于气候与海洋环境的变化有重要影响[1]，由于在结冰海域内，海水的水质在各种干扰因素条件下会有很强的波动性，需要对该海域内的海洋环境进行实时监测。但由于常规监测设备耐低温性能差且易损毁、现场人工操作危险性高且工作效率低、海上突发环境风险性高等客观问题的存在，加之针对于重污染监管区的长序列环境数据积累、重点海域特征参数在线监控、水质状况指标快速解析等需求，使得冰区海洋生态环境监测浮标成为一种优先选择的支撑性海洋生态环境监管手段。

以航标为例，为了尽可能降低海冰对于正常浮标的损坏，北方港口在冰期来临前大都会把正常浮标更换为冰标，次年3—4月根据冰情再更换回来。数据显示：1991—1995年，北海航海保障中心季节性航标更换的数量为763座，而2011—2015年，季节性航标更换数量上升到6165座[2]，随着海洋经济的不断开发，浮标更换的工作量日益繁重，不仅不能获得良好的航标性能，还增大了海上施工人员工作的危险性。

我国国家海洋技术中心2003年就在北极安装了自行研制的极区卫星跟踪水文气象观测浮标，并成功获得北极地区连续的海冰与气象数据[3]。但极区浮标通常是通过在冰层上打孔，将浮标固定在冰层之上[4]，不会出现季节性冰期消融就无须考虑破冰问题，当布放在漂流冰上时，海冰的观测数据即为漂流轨迹数据[5]。因此在我国的周期性结冰海域也无法应用此类海洋监测浮标，亟需研制一种有一定抗冰能力的浮标结构。

目前国内外还没有以抗冰为需求的浮标设计理论体系，抗冰浮标的研究涉及冰力学、流体力学、结构力学、浮体静力学以及系泊等相关理论知识，是多学科知识交叉问题，具有一定的学术前沿性。

1 提出问题

1.1 浮标被推翻

浮标在严重冰情时受到的冰力很大，由于系泊存在使得浮标不能跟随冰排移动，在冰力的作用下浮标的姿态将发生改变，冰力与系泊力给浮标施加一个倾覆力矩，且由于一般浮标储备浮力空间不足，浮标排水体积改变产生的复原力矩远远不能达到恢复正常姿态的需求，因此造成浮标的倾覆失效。导致太阳能板与风力发电仪器无法正常工作，切断了浮标的能源供给，无法连续完成日常监测任务。

1.2 浮标整体入水

当标体无法破冰时，浮标的正浮姿态发生偏转，倾斜角度加大，冰排有沿着标体侧壁爬升至顶部的趋势，同时浮标受到向下的压力被冰排压至海面以下，浮标主体全部入水，上部太阳能板或风力发电装置将遭受海冰的冲击破坏。

1.3 系泊失效

一般海域内浮标的系泊设计不考虑海冰因素，但冰区内海冰的水平作用力对于浮标造成的响应要远高于风浪流等载荷，冰区浮标的失踪率也要远远高于常规海域内的浮标，最主要原因就是系泊缆绳断裂，浮标在冰力作用下摆脱系泊缆绳的限制。系泊是保证浮标被限制在某一海域内不发生丢失的唯一手段，当水平系泊力无法约束冰力作用下的浮标运动时，将引起浮标的系泊失效。

2 研究方法

2.1 理论依据

该种浮标设计思路具有开创性，是首次以抵抗海冰为主要需求的浮标设计方案，由于浮标与海冰相互作用时的姿态大都具有一定倾角。为保证浮标不会发生整体入水致使上部自发电结构损毁，标体边缘水密舱室顶端到达海平面相比标体正浮时的姿态有一倾斜角度，将这一倾角设置为在冰力作用下标体允许的最大倾角。

由于浮标与海冰相互作用时浮标侧壁呈正锥体斜面形式，无法保持倒锥体斜面形式进行破冰，因此需要根据水密性储备浮力空间的基本尺度明确浮标的正倒锥。设计破最大厚度冰的结构方案，只需考虑最危险倾角下标体能否破冰即可。确定标体形式及各角度的方法如图1所示。其中α为标体侧壁与底部之间夹角，β为标体允许的最大倾角，γ为标体姿态处于最大倾角时，侧壁与海平面之间的夹角。

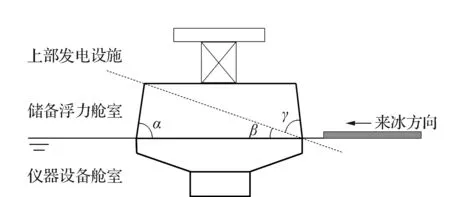
图1 标体结构简图及角度

研究表明，锥体的水平静冰力主要由冰的弯曲强度与上爬力两部分组成，计算窄锥体时通常不考虑上爬力[6]，即在海冰爬升至标体顶部之前完成破冰。取Hirayama-Obara冰力计算模型[7]进行浮标侧壁所受水平冰力F冰X的计算如式(1)所示：

(1)

式中：B为经验系数，取3.7；σf为海冰弯曲强度，Pa；D′为海平面处锥体的直径，m；由于海平面处浮标的吃水线非正圆形，可以取来冰方向的水线宽度近似计算,m；t为海冰厚度，m；LC为海冰的特征长度，由式(2)得到：

(2)

式中：E为海冰的弹性模量，E=5×108Pa；ρw为海水密度，取1.025×103kg/m3；g为重力加速度，取9.8 m/s2。

以上公式计算的是海冰作用于带有一定刚度的锥体结构其水平方向的极值静冰力，竖直方向的极值静冰力F冰Y可以通过斜面角度γ进行计算，如式(3)：

(3)

同时可以获得该倾角下由于上部水密空间入水所增加的实际最大储备浮力增值F″浮，如式(4)。

F″浮=ρwV′排g

(4)

此外对于浮标姿态有重要影响的还有系泊力，详细的受力分析如图2所示。图中虚线表示将倾斜的力分解为水平和垂直两个方向。

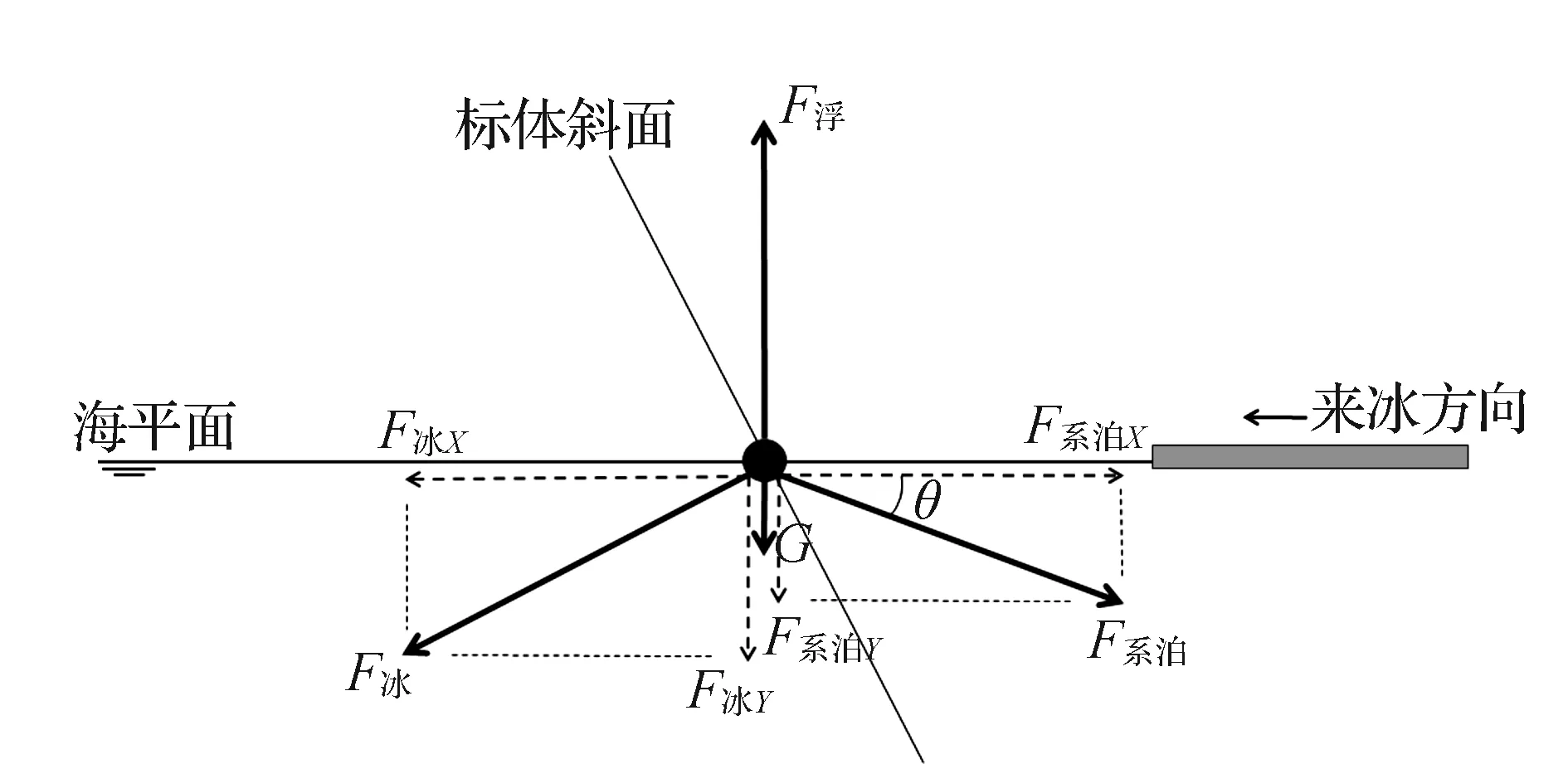
图2 标体受力分析简图

当浮标成功破冰前，处于动态平衡状态，水平与垂直的方向合力为零，当浮标入水体积继续增大时，冰力与系泊力不发生改变，总浮力增大，进而可使冰排发生弯曲破坏。通过受力分析可得以下结论，如式(5)、式(6)：

水平方向：

F冰X=F系泊X

(5)

垂直方向：

F浮=G+F冰Y+F系泊Y

(6)

式中：F系泊Y=tanθ·F系泊X，θ角为绷紧的系泊缆绳与海平面之间的夹角。

由于重力G始终不发生改变，抵消了一部分总浮力F浮，因此动态平衡时有式(7)：

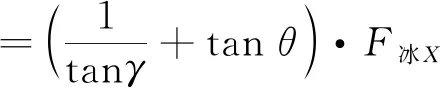
(7)

当水密标体实际增加的最大储备浮力值F″浮大于海冰发生弯曲破坏时需要的储备浮力值F′浮时，即可达到成功破冰的目的。

3 结果分析

小型浮标基本尺度以浮标锥体水密结构最大直径3 m，水密部分海平面以上最大高度1 m为例，针对储备浮力进行设计计算。通过对水线以上结构进行CAD软件建模得到不同α角度下(50°～88°)，对应浮标倾斜至规定的最大倾角β时的排水体积增量V′排以及侧壁与海平面之间的夹角γ，由公式(4)计算得到如图3所示的实际最大储备浮力值F″浮。

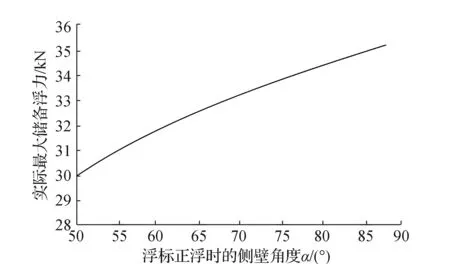
图3 不同α角度下标体的实际最大储备浮力值

图3可以看出在该基本尺度下，浮标的设计储备浮力基本大于30 kN，但随着α角度的增加，储备浮力增幅较小。当锥体斜面α角度继续增大时(α>88°)，γ角度大于70°，超出海冰只发生弯曲破坏的计算范围，海冰将发生挤压破碎，冰力会显著提高[8-9]，因此仅以海冰发生弯曲破坏为目标，浮标在该基本尺度下增加的实际浮力值最大约为35.3 kN。

以目标冰厚0.1 m为例，根据公式(1)、式(2)、式(3)、式(5)、式(7)可以计算该冰厚下浮标处于不同α角度时破冰需要的储备浮力值F″浮。其中海冰弯曲强度取σf=700 kPa；采用单点系泊，系泊点位置距海底7 m，系泊缆总长30 m，此时tanθ=0.2447。将其与浮标的实际最大储备浮力值F′浮比较，即可判断不同角度浮标的结构设计方案是否具有抗冰能力。判断方法以图4为例：当α<71.5°时，F′浮F″浮，即浮标结构具有破0.1 m厚冰的能力。

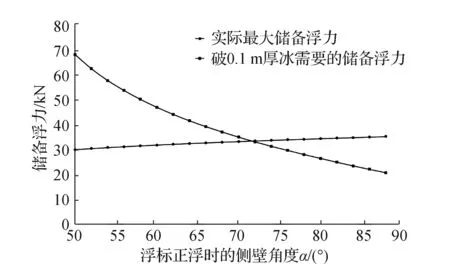
图4 不同α角度下标体破0.1 m厚冰的能力

当设计冰厚不变，改变浮标侧壁角度时，随着α角度增加，破冰需要的储备浮力值F″浮呈明显减小趋势，对于浮标结构其破冰行为安全性更高。但α角度的最大值由γ角决定，因此在设计范围允许内尽可能增大α角度为结构设计的优先方案。

取该基本尺度下浮标侧壁角度最大值α=88°为例，研究表明：随着冰厚的增大，标体破冰需要的储备浮力增幅明显加大，浮标最大可破13.5 cm厚的冰。在相同的海冰条件下，浮标破冰需要的储备浮力值都相同，增大浮标的最大储备浮力(增大基本尺度)即可有效提高标体的抗冰能力。

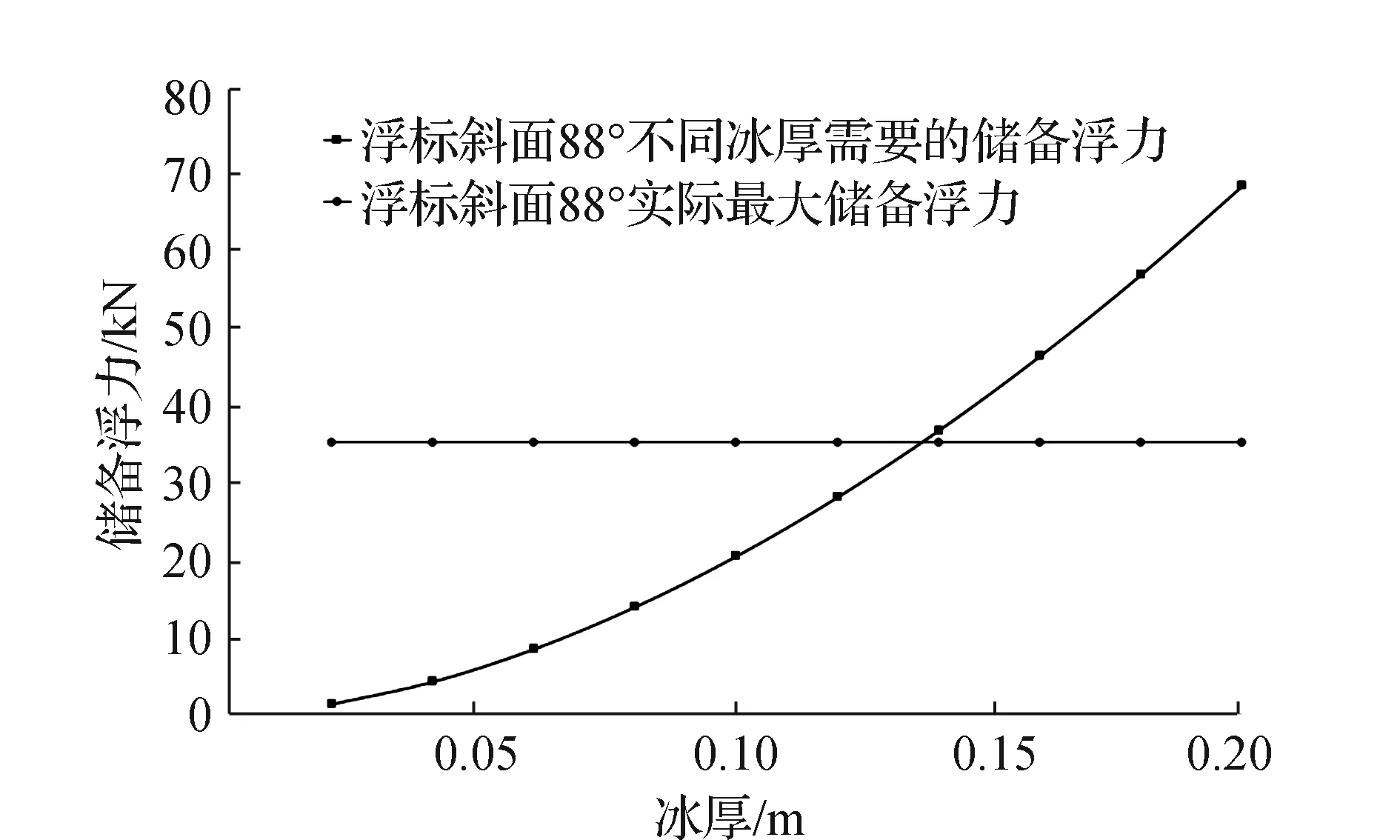
图5 α=88°时标体破不同厚度冰的能力

除此之外，海水深度一定(H=7 m)时，还可以通过延长系泊缆绳的长度进一步加大浮标的抗冰能力。图6为不同冰厚下，系泊力的垂向分量F系泊Y随系泊缆绳长度的变化趋势，曲线开始时F系泊Y迅速降低，后降幅逐渐趋于零。在考虑经济性的同时，适度增大系泊缆长度，可减小tanθ值，根据式(6)与式(7)长系泊缆破冰需要的储备浮力相比短系泊缆可大幅降低。

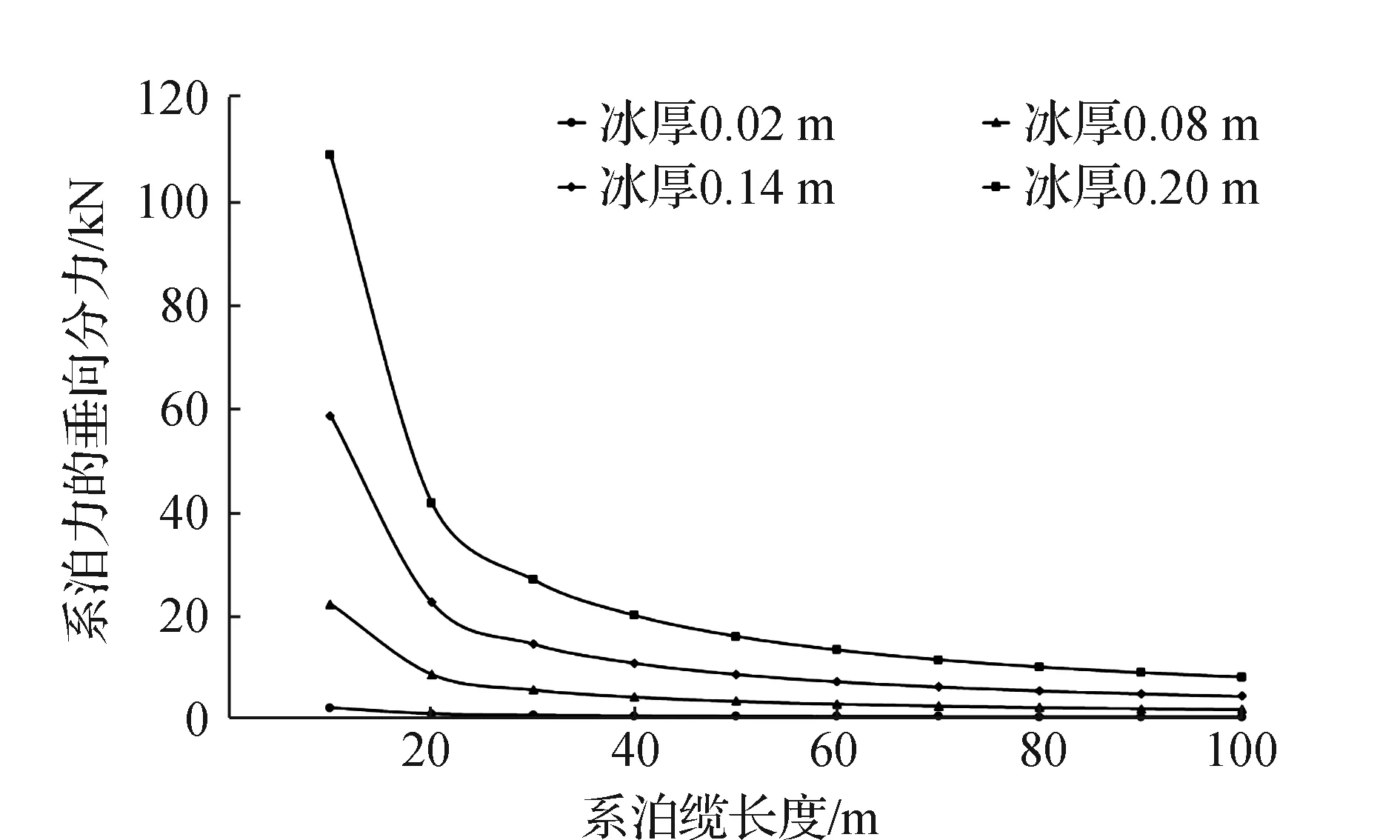
图6 不同系泊缆长度下系泊力的垂向分量

4 结 语

根据分析计算，小型浮标利用储备浮力使冰排发生弯曲破坏存在理论性可能，但基本尺度较小时无法提供足够的水密性空间，抗冰能力较差。此外在常规的浮标设计过程中，储备浮力按照以上抗冰理论方法进行设计，浮标的基本尺度越大、系泊缆绳长度越长，可以抵抗越厚的海冰。