海上风电大直径单桩基础固有频率影响因素的数值分析

孙肖菲，马东，苏冠瑜，吴伙桂，陈帮

(明阳智慧能源集团股份公司，广东 中山 528400)

海上风机基础的制作和安装费用约占风电机组工程总成本的20%～30%[1]。目前，国内海上风电场的风电基础结构类型主要有重力式基础、单桩基础、导管架基础、负压桶式基础、浮置式基础等结构形式[2]。其中，大直径单桩具有结构型式简单，设计方法成熟以及施工维护较为方便等优点，是海上风电场近浅海水域开发过程中应用最多的基础型式[3]。由于风、波浪、海流等外部环境荷载作用，使风电结构承受相当大的水平力和弯矩荷载。整机的低阶固有频率应避开叶轮转动频率区间，以保证机组整体不会发生共振，满足安全使用的要求。为此，重点分析大直径桩的桩土相互作用以及桩内土芯、冲刷深度等因素对整机固有频率的影响。

1 桩土作用数值模型验证

1.1 有限元模型

验证阶段所选取的黏土模型是出自Matlock[4]在Sabine地区的试桩及土壤材料，荷载作用位置距泥面处0.3 m，钢管桩的入土深度为12.81 m。三轴试验中最大主应力差一半时的应变值ε50取值为0.02，量纲一的量经验参数J取值为0.5。黏土及桩基参数见表1。具体的黏土模型网格划分方式见图1。

表1 Matlock试验材料参数

图1 黏土有限元模型

砂土模型则取自Pedro[5]等人在水下中密砂和粉砂为主的土层中进行的一系列单桩试验，荷载作用的位置距泥面处2.1 m，钢筋混凝土桩的入土深度为14.5 m。现场试验土层分为2层，上层为水下中密砂，分布在距离泥面4 m范围的土层；下层为粉砂，分布在中密砂层以下的土层中。砂土地基的初始反应模量为13.8 MN/m3。砂土及桩基参数见表2。具体的砂土模型网格划分方式见图2。

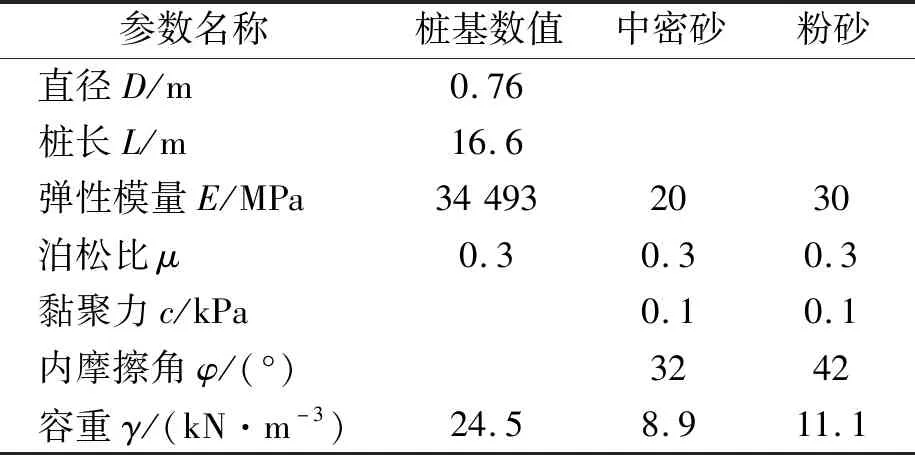
表2 Pedro试验材料参数

图2 砂土有限元模型

采用有限元分析技术分析水平向作用下小直径桩的桩身及桩周土特性。由于桩基、土体在正常承载力的作用下均变形相对较小，因此，土体网格采用拉格朗日单元进行计算。土体模型采用8节点实体单元，桩基采用线弹性模型，土体遵循Mohr-coulomb塑性准则。为避免边界层效应影响，桩周土体直径取24倍桩径，桩端至底部取6倍桩径。对模型底部边界施加X、Y、Z方向位移约束，侧向曲面边界施加X、Y方向位移约束，侧向直面边界施加Y方向位移约束。桩与土体界面间建立面-面接触关系，法向接触采用硬接触，切向接触采用罚函数法。

1.2 模型验证分析

黏土层的验证分析中，参照Matlock试验设置，在桩顶施加17.8，35.6，80.1 kN水平荷载，对比分析所得到的计算结果与现场试桩试验结果、API规范计算结果，结果见图3、4。

图3 沿桩身弯矩分布

图4 桩顶位移及荷载

砂土层分析参照Pedro等的试验设置，在桩顶施加了138 kN的水平荷载，计算结果与现场试桩试验结果、API规范计算结果进行对比分析，对比结果见图5、6。

图5 沿桩身弯矩分布

图6 桩顶位移及荷载

从有限元计算所得沿桩身弯矩、桩顶位移-荷载曲线与实测值的对比分析可以看出，对于黏土，有限元方法的弯矩计算结果与实测值及API规范计算结果有一定的偏差，但偏差很小，在可接受的范围内；有限元方法得到的桩顶位移-荷载曲线相较于API规范方法更接近实测值。

对于砂土，有限元方法所得沿桩身弯矩、桩顶位移-荷载曲线均比API规范方法更接近实测值。

上述结果表明，本文所选用的桩-土有限元模型较为合理和准确。因此，将该模型继续用于海上风电大直径单桩的整机固有频率研究中。

2 风电机组整机固有频率

海上风电大直径单桩结构需进行整机模态分析，使得固有频率避开波浪、叶轮转动等激励荷载频率，避免共振情况的发生。适当简化模型，利用经典解析计算理论或有限元计算方法预测结构自振频率，以便指导工程设计。依据有限元方法对风电机组基础结构及整机系统，即叶片+轮毂+机舱+塔筒+基础+地基系统进行模态计算分析。计算风机基础与整机系统的多阶模态，用以评价基础结构设计是否满足海上风电机组动力特性需求。

2.1 大直径单桩基础整机有限元模型

采用有限元分析方法建立三维有限元模型，见图7。

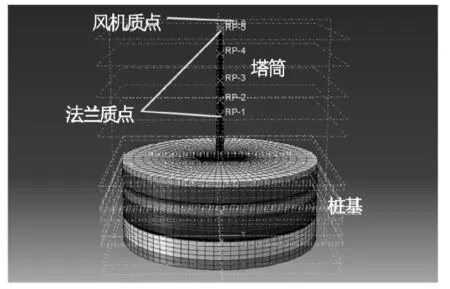
图7 海上风电整机有限元模型

风电机组机舱和叶片所组成的局部系统及其他附属构件可简化为质点[6]。因此，风电机组共设置5个法兰质点，叶片+轮毂+机舱质量以施加质点的方式分布在三者的重心坐标处。其中，法兰质量大小自下至上依次为8.11，12.93，51.90，6.53，1.67 t/m3；叶片+轮毂+机舱质量大小为425.56 t/m3。水动附加质量对于海上风电大直径单桩体系的一阶固有频率的影响可忽略[7]，故本章建模时未考虑水体的影响。

地基土体共划分15层，多层土网格划分方式见图8。模型的桩周径向长度取24倍管径，桩端至底部取6倍桩径。位移约束条件以及模型面-面接触关系与第1.1一致，此处不再赘述。塔筒长度为91 m，泥面以上桩基长度为47.28 m，泥面以下桩径为8.5 m，单桩入土深度为51 m。

桩基础及塔筒采用线弹性材料，地基土体采用8节点实体单元类型，桩-土相互作用采用无连续体效应模拟，且遵循Mohr-Coulomb弹塑性屈服准则。各土层材料参数通过现场地勘报告获得，见表3。

2.2 有限元方法的计算结果对比分析

对于传统的梁单元及非线性弹簧单元体系计算方法，桩体、塔筒采用梁单元模拟，地基基础借助侧阻T-Z曲线和桩端Q-Z曲线、水平向P-Y曲线实现桩土相互作用，P-Y、T-Z、Q-Z曲线可根据地勘报告提供土的摩擦角、不排水剪强度等参数描述。分析时采纳API规范中所推荐的P-Y曲线法，此方法被公认为比较有效的桩土作用分析方法，此处将其定义为“方法一”；将实体单元模型(有限元方法)定义为“方法二”；使用两种方法分别计算大直径单桩结构的整机一、二阶固有频率，提取计算结果并对比，见图9。

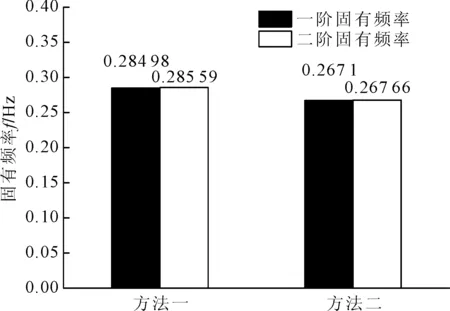
图9 有限元方法影响下的固有频率分析

由图9可知，有限元方法计算得到的一、二阶固有频率要明显大于传统的“梁单元+土壤非线性弹簧单元”方法所得结果，这也与众多学者研究得到的结论相一致[8～9]。说明对于大直径单桩结构而言，基于梁单元计算方法得到的计算结果存在一定的误差，主要原因是由于此方法求得的土壤刚度偏小导致。

2.3 桩内土芯及叶片+轮毂+机舱影响分析

表4为固有频率的影响。

表4 固有频率影响分析 Hz

由表4可知，在考虑桩内土芯时，整机模型的一、二阶固有频率减小约为0.007%，表明桩内土芯对整机一、二阶固有频率影响很小。因此，在使用有限元方法分析海上风机固有频率时，可忽略桩内土芯的影响。另外，通过表4可以看出，是否考虑叶片+轮毂+机舱对整机一、二阶固有频率有显著的影响。

2.4 表层土置换措施对固有频率影响分析

在原有限元模型的基础上分析2种桩内土层置换方式，一种方式是通过挖除泥面以下5 m范围内的桩内土芯，并用C15混凝土灌注至泥面以上5 m范围内，此时，整机一阶固有频率为0.288 31 Hz，整机的二阶固有频率为0.288 95 Hz。另一种方式是挖除泥面下10 m范围内的桩内土芯，同样用C15混凝土作为替换材料灌注至泥面处，此时，整机一阶固有频率为0.290 28 Hz，整机二阶固有频率为0.290 60 Hz。2种置换并填充桩内土层的做法对固有频率有一定提升，在综合考虑施工可行性和成本因素的情况下，可以作为增大钢管桩直径的一种替代措施。

2.5 冲刷深度影响分析

在波浪、潮流荷载作用下，风电桩基础周围土体会产生局部侵蚀、冲刷，影响桩基的性能[10]。国内外设计中，结构计算预留冲刷深度有时可达6 m以上，但只考虑了对其承载力的影响，很少考虑对系统自振频率的影响[11]。对海床冲刷深度为0.5～5 m范围内的一、二阶整机固有频率进行有限元计算分析，见图10、11。

图10 冲刷深度对一阶固有频率影响分析

图11 冲刷深度对二阶固有频率影响分析

随着冲刷深度的增加，一、二阶固有频率均有所减小。方法一计算结果仍明显大于方法二结果。在冲刷深度从0.5 m增加至5 m范围内，一、二阶整机固有频率减小的幅度均较小。

3 结论

1)基于梁单元及非线性弹簧单元体系计算的一、二阶固有频率均明显小于基于实体单元有限元计算的一、二阶固有频率，因此传统p-y方法在求解海上风电大直径单桩的固有频率时结果偏小，需通过试桩试验等方法对其进行进一步分析。

2)桩内土芯对整机一、二阶固有频率影响甚微，在分析海上风机固有频率时，可忽略桩内土芯的影响。

3)在冲刷深度一定范围内，整机一、二阶整机固有频率增长的幅度均较小，此时冲刷深度可不作为决定一二阶固有频率的主要因素。