让思维导图“导”出学生思维的灵气
何正锋

【摘要】通过思维导图的应用能够全面地调动左脑对逻辑、顺序、条例、文字、数字以及调动右脑对图像、想象、颜色、空间、整体等的思维,使得大脑的潜能和创造力得到最充分的开发,从而极大地充分激发人们的科学创造性和思维能力。思维导图的应用于我国小学和初中数学的教学中既完全具备了学习方法和工具的强大实用性和优势,又充分符合了小学生的学习思维过程和创造性认知的特点。
【关键词】思维导图;小学数学;思维能力
波利亚认为,教师要把三分之一的努力花在学生教些基本的数学上,而把三分之二的努力花在培养对学生有益的数学思维表达方法和良好的思维习惯上。精彩的课堂数学和思维课堂教育不一定要强调教学形式如何新颖,内容如何丰满,当教师能够引领学生在精彩的数学和思维的世界里自由遨游时,我们的基本数学思维在课堂就已经可以说明它是有效的、深刻的、灵动的。那么,如何才能实现?用思维导向图可以实现我们这个愿望。思维导图是二十世纪英国著名学者东尼·博赞(tonybuzan)在20世纪60年代所创的一种新型记忆与思维方法。它主要是表达各种发散性抽象思维的有效工具,可应用于所有认知功能领域,尤其是记忆、创造、学习和各种形式的抽象思考,它被研究者描述为“大脑的瑞士军刀”。它既可以是呈现数学知识的网络,是间接组织学生陈述抽象性知识的良好工具,同时也可以直接呈现思维过程,是组织程序性知识的良好工具。思维导图工具应用于我国中小学数学的教学中既完全具备了学习思维导图工具的强大功能和优势,又充分符合了中小学生的学习具体思维过程和其认知特点。一方面,思维导图可以通过图像、色彩等手段,把难于表达的隐性数学知识转化成一种形象化的显性数学知识,使得中小学生在学的具体思维过程中完全能够很好地理解和领悟隐性的知识。另一方面,学生在自主学习的过程中,可以通過思维导图自主地建构知识结构,加工整理数学概念,参与组织数学抽象性问题的分析和讨论,做到对于数学知识的深入系统理解和有效运用,培养小学生形象思维的能力和对信息处理的能力,以新的高度有效地充分开发小学生的思维潜力。在小学数学教学中,学生思维形象极其活跃,有利于教师在教学中引入思维导向图来辅助教学。
一、“导”出学生思维的发散性
发散性的思维图模式又称发散性辐射求异思维或发散性求异思维,是指学生的大脑在发散性思维时呈现出一种高度扩散和延展状态的思维导向图模式,从一个目标或者事物的思维中心或者起点开始出发,沿着不同的方向,各个的角度向学生提出各种的设想,寻找各种的途径,解决具体的问题。而发散性思维的导向图模式能让学生用发散性的思维把每一个人的想法都按需要从一个思维中心或者主题方向放射出去,进行360度全方位的辐射和多角度的延展。
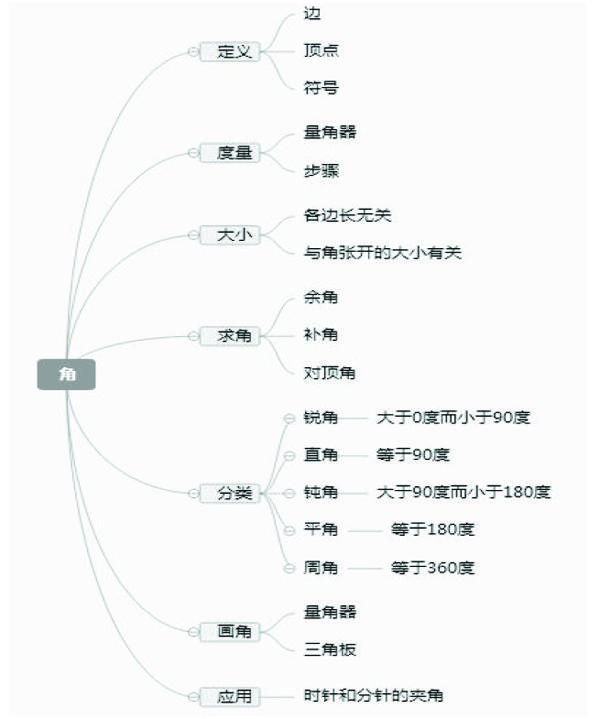
教师引导学生在整理和复习《角》的思维联想相关内容和知识的时候,先引导学生提出一个联想的关键词——角,然后可以引导其他学生尽兴地思考这个联想的关键词,把自己需要联想的关键词和内容分成几个版块记录下来,再按照联想的版块一级一级地进行各个分支的联想,能够进行联想得到多少就能够进行联想得到多少。学生可以与其他同学进行商量,向教师和学生寻求联想上的帮助,完善自己的联想和思维导图。在课堂教学中,有一位学生绘制了下面的联想和思维导图。从这幅思维导图中,我们可以清楚地看出,学生在导图绘制时的思维发散导图过程,越是层层往下,分支越多,联想得到的关键词和内容也就越多。值得一提的是,在“应用”版块,学生已经能联想到“九点整”“六点整”“一点整”等一系列更深层次的思维导图问题。可见,对学生的思维导图发散的能力非常强。思维导图促进了学生的“学”和教师的“教”,为学生提供了一种积极活跃的探讨氛围,以发散性的思维激发学生的兴趣,以图示的方式给学生提供了无限遐想的思维空间。
二、“导”出学生思维的独创性
思维导图在解决问题中运用的是“数形结合”的思想。作为数学思维,数形结合的应用就是借助于形的几何直观性来阐明数之间的某种关系。因此,在教学实践中,学生独立联想和绘制思维导图的绘制过程就是学生自主创造的一种实践过程,学生需要具有广泛独立联想的思维能力,可以根据自己的兴趣喜好自由设计绘制符合条件的各种思维方法和导图。在对思维想法和导图的设计绘制和展示过程中,学生先要对问题进行大量的思考,然后把自己头脑中产生和迸发出的各种思维想法,用文字和图画的各种表现方式完美地组合在一起。当学生在课堂中构建自己的独立联想思维方法和导图后,与其他教师对学生的思维作品内容进行了比较时,还可能会产生新的思维想法,这样就有利于更好地培养和提高学生的自主创新探索精神和自主实践的能力。教师和学生的绘制和认识思维过程实际上是由学生感性到理性再到感性循环往复、螺旋上升的一个过程,为此,学生通过对思维导向图的绘制和展示可以更好地帮助教师和学生在更高的层次上引导学生展开有理有据的探索和思辨,提高主动地应用所学知识主动解决实际问题的意识和能力,让教师和学生的绘制思维导图变得更具独创性。
三、“导”出学生数学模型建构
教师要立足于学生已有的知识和生活经验,引导学生亲历学习过程,将实际问题抽象成数学模型并进行解释与应用,让学生获得发现和解决数学问题的机会,让学生能够通过“经历”和“体验"”来了解数学思想和模型理论建构的具体形成和应用过程,因为具体可操作性强可以清楚地让学生了解四年级的学生通过什么样的数学活动、什么思维方式可以获得数学知识技能及其思想方法。在教学人教版四年级上册《沏茶问题》的过程中,以平时已经帮家里做了大量的家务,有一定的家庭生活经验的四年级的学生作为课堂教学的起点,把一个学生自己比较熟悉的“沏茶”问题作为教学的引例,通过自己设计学生沏茶活动的顺序和时间,再通过与同学的交流,便有了学生初步的体会。教师不仅要引导学生考虑做一件事情的时间安排和顺序还要引导学生考虑自己是否可以“同时做”这两个问题思维的方式和角度。学生可以通过用数学思维的导向图对学生进行观察和比较为什么同样可以增加一件新的事情,一种方案的增加时间为什么不变,而另一种方案的增加时间为什么变了呢?
通过观察和横向的比较,让学生进一步体会到两件事情横向发展的顺序和我们同时可以做的两种事情思维方式和角度的不同,所以我们花的时间也可能会随着不同。通过对观察和纵向的比较和分析,让学生进一步地明白,我们同时可以一起完成的两件事情越多,那么越可能节省时间的基本道理。学生也从中形成了自己的知识体系,建立自己的时间管理模型。
思维导图的出现让数学不再冷冷清清,不再是单调乏味,而是色彩缤纷,犹如游走在艺术之境,让我们缔造美、欣赏美、使用美。思维导图促进了学生的“学”和教师的“教”,为师生提供了一种积极活跃的探讨氛围,打破了学生的思维定式,借助思维导图这“大脑使用的说明书”,让学生彻底爱上数学,爱上思维,需要我们去努力挖掘、探讨、研究,以图示的方式给学生提供了无限遐想的思维空间,让学生在学习中体验到学习的快乐。
参考文献:
[1]东尼·博赞.教学思维模式导图:让您了解你的大脑如何灵活使用的一本说明书[M].外语教学与研究出版社,2002.
[2]刘艳.你一旦开学就有机会的现代英语教学思维模式导图[M].大学中国语言文化与经济发展社会科学技术研究出版社,2017.

