一种风电机组的定场址评估优化方法*

王瑞良，孙 勇，刘 为，李 涛

（1.浙江运达风电股份有限公司，杭州 310012；2.浙江省风力发电技术重点实验室，杭州 310000）

0 前言

风电是目前最有竞争力的可再生能源发电生力军[1]。近年来，风电行业发展迅猛，中国风电装机量一直稳居世界第一排名，随着风电行业的发展以及平价市场的普及，针对实际的投标项目，各整机厂家在机组塔架设计上均采用定场址计算来保障机组的经济性与可靠性。定场址计算的主要数据来源于风资源的微观选址报告，其中确定风电场风力发电机选型以及安装高度的一个重要参数就是风切变指数[2-4]。近年来，风能资源利用力度逐渐加大，近地风切变的研究工作越来越受重视[5-7]。

微观选址报告中一般为一年以上的测风数据，风切变的拟合是采用不同高度下的年平均风速来计算的，采用该方法拟合的风切进行载荷评估，并不能真实反映场址的载荷状态，甚至低估了风场的实际载荷，严重影响机组的可靠性以及疲劳寿命，因此开展风切对载荷影响的评估显得尤为必要。

本文基于传统的风切计算方法从统计学角度进行分析，依据风场实测数据得到载荷计算输入的风切变，并通过仿真与测试比对，验证方法的可行性。

1 传统风切变计算方法

传统计算风切变有两种方法，一种是采用不同高度的全年平均风速求风切变指数值；另一种是求每个10 min的风切变数据。

1.1 全年平均风速法

该方法是微观选址常用的方法，首先计算不同高度的年平均风速，由不同高度的年平均风速依据式（2）来计算风切[8-9]：

式中：vi(h)为高度为h的600 s风速均值；n为测得的样本总数；α 为风切变。

1.2 风切取平均法

本方法计算每个600 s 的风切值，然后对数据采集周期内的所有风切取平均。

2 概率统计法

在定场址的载荷评估中，往往采用上述的风切取平均的方法，而实际的风机载荷与风切又不是单纯的线性关系，采用均值往往会低估了在该风场下的实际载荷，严重影响风机的可靠性。

本文依据测试数据，提出了采用正态分布概率法来等效评估风机载荷。某风场风切实测数据如图1所示。

图1 某风场风切实测数据

采用概率统计法既考虑了平均风切变，同时也考虑风切的波动大小即标准差带来的影响。

假定风切服从正态分布，定场址下的载荷输入风切计算方法为：

式中：αsite为定场址输入风切，为风切标准差。

3 数据测试

为验证概率方法的可靠性，对某机组的风切变以及载荷进行了测试与数据分析，如表1所示。测试机组如图2所示。

表1 测试机组基本信息

图2 测试机组

本文对叶片挥舞方向的疲劳载荷进行了数据分析，得到测试机组每个风速下的1 Hz 等效疲劳，等效疲劳载荷计算方法[10]如下：

式中：LN为等效疲劳载荷；Li为区间i内的载荷变化范围；ni为区间i内的雨流个数；m为材料系数；N为循坏次数。

由于风机设计寿命一般为20 年，因此不仅要考虑1 Hz 的疲劳载荷，还要联合年平均风速分布计算20的等效疲劳载荷。

假定风场风速服从以6 m/s 平均风速的瑞丽分布，那么累计概率分布方程如下：

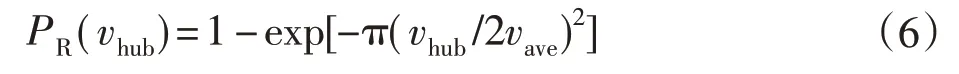
式中：vave为年平均风速；vhub为风速；其概率密度分布图如图3所示。

图3 风速概率密度分布

4 仿真与测试载荷对比

本文根据测试机组的场区数据计算得到，风场的实际风切变数据为0.24，该数据对应的90 分位数的值为0.65；本文基于Bladed软件对载荷进行仿真模拟并于实测数据进行对比[11]。风切散点图如图4 所示；风切概率分布柱状图如图5所示。

图4 风切散点图

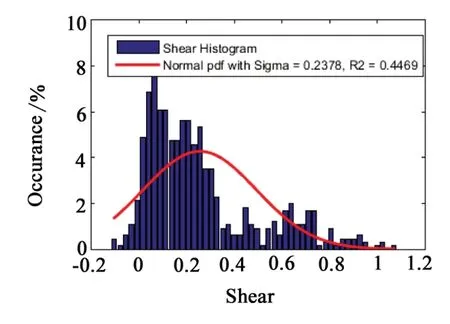
图5 风切概率分布柱状图

在平均风切0.24 下仿真的各风速下等效疲劳载荷与测试载荷对比如图6～7所示。

图6 平均风切0.24 下仿真与测试等效疲劳载荷对比

图7 90%分位数风切下仿真与等效疲劳载荷对比

假定年小时数为8 766 h，联合式（6）可求得20年的等效疲劳载荷如表2～3所示。

表2 平均风切下20年等效疲劳

表3 90%概率下风切20年等效疲劳

通过上述统计分析，采用平均风切变0.24 仿真的疲劳载荷低于测试载荷，而采用正态分布90%分位数的风切变作为定场址评估的风切输入计算得到的统计结果更接近疲劳载荷，而且比实际风场载荷略大，保障了机组的可靠性。

5 结束语

本文通过对风切变以及疲劳载荷的研究，提出了一种采用正态分布统计方法来有效评估风机载荷的方法，并且通过与测试数据的对比分析发现，该方法较传统方法能更准确地评估叶片实际的疲劳损伤，具有一定的实际指导意义。