XZ-Ⅱ型旋转式倒立摆智能非线性控制实验

陈虹丽，刘凌风，夏晓靖，王显峰

（1.哈尔滨工程大学智能科学与工程学院，哈尔滨 150001；2.上海机电工程研究所，上海 201109）

0 引言

倒立摆控制是一类十分典型的非线性控制问题，文献［1-2］中对倒立摆系统采用滑模控制算法，文献［3］中利用拉格朗日方程对倒立摆系统建模，设计PID和反向传播（Back propagation，BP）神经网络控制演示平台，文献［4-6］中将非线性模型转化为线性系统，再进行极点配置和PID控制等，文献［7-8］中利用牛顿第二定律，建立XZ-Ⅱ型倒立摆系统模型，将倒立摆非线性模型转化为线性系统，进行状态反馈控制［9］及状态观测器设计。本文将科研成果［10］应用到倒立摆非线性控制实验中，直接进行非线性输出（负）反馈控制器设计。

1 XZ-Ⅱ型倒立摆控制器设计

XZ-Ⅱ型倒立摆系统结构和模型如图1 所示。

图1 系统结构和模型

根据牛顿力学，XZ-Ⅱ型倒立摆非线性模型为［11］：

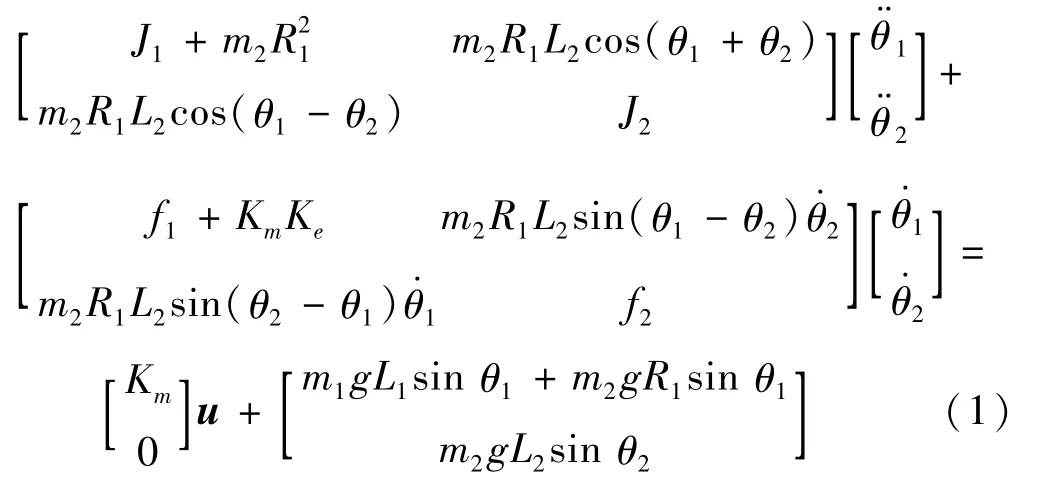
式中：u为电动机的电压，θ1、θ2分别为旋臂、摆杆与纵轴的夹角。各机械参数含义见表1。

表1 机械参数及数据

显然，式（1）的相对阶数［12］r＝2，对其进行坐标变换

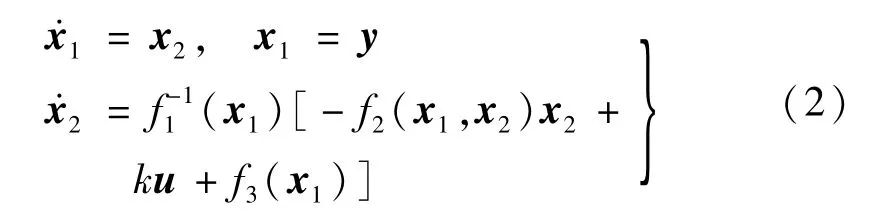
式中：

式（2）可改写为：

设计虚拟控制ux，使y最终在有界误差范围内光滑达到有界期望轨迹yd。这里要求有界。利用式（4）将虚拟控制转化为作用在倒立摆上的实际控制。在虚拟控制定义下，输出动态方程为：

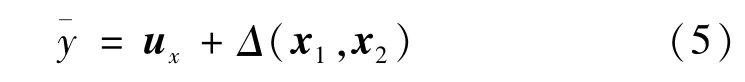
式中，

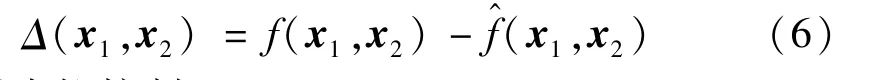
选择虚拟控制：

式中：u1为引入的动态补偿器的输出项，是线性部分，用于稳定动态误差；u2为自适应控制项，用来抵消Δ（x1，x2）。控制原理如图2 所示。

图2 控制原理图

将虚拟控制式（7）代入式（5），得：

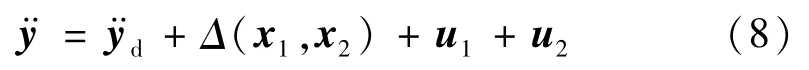
下面分别给出u1、u2的设计过程。

2 动态补偿器设计

定义输出跟踪误差：

将式（8）代入，得：

设线性动态补偿器状态方程为：

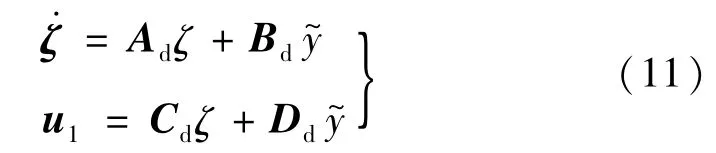
式中，ζ∈R2为线性动态补偿器的状态。由式（10）、（11）得跟踪误差动态方程：

3 自适应控制项设计

（x1，x2）由非线性神经网络自适应得到，实验中采用BP神经网络［3］。自适应控制项

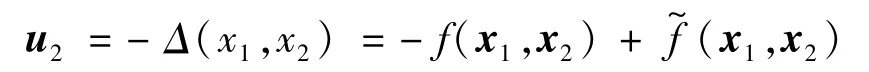
在自适应控制项设计中，需要用到速度信息，实际工程中，它们无法通过测量直接获得，即使能够测量得到，也带有一定的随机测量误差。所以设计一个Kalman滤波器来估计它们［13-14］。

4 Kalman滤波器的设计

5 实验步骤及结果分析

图3 学生实验控制结果

图4 基于问题的探究式学习

学生成绩定量分析见表2。

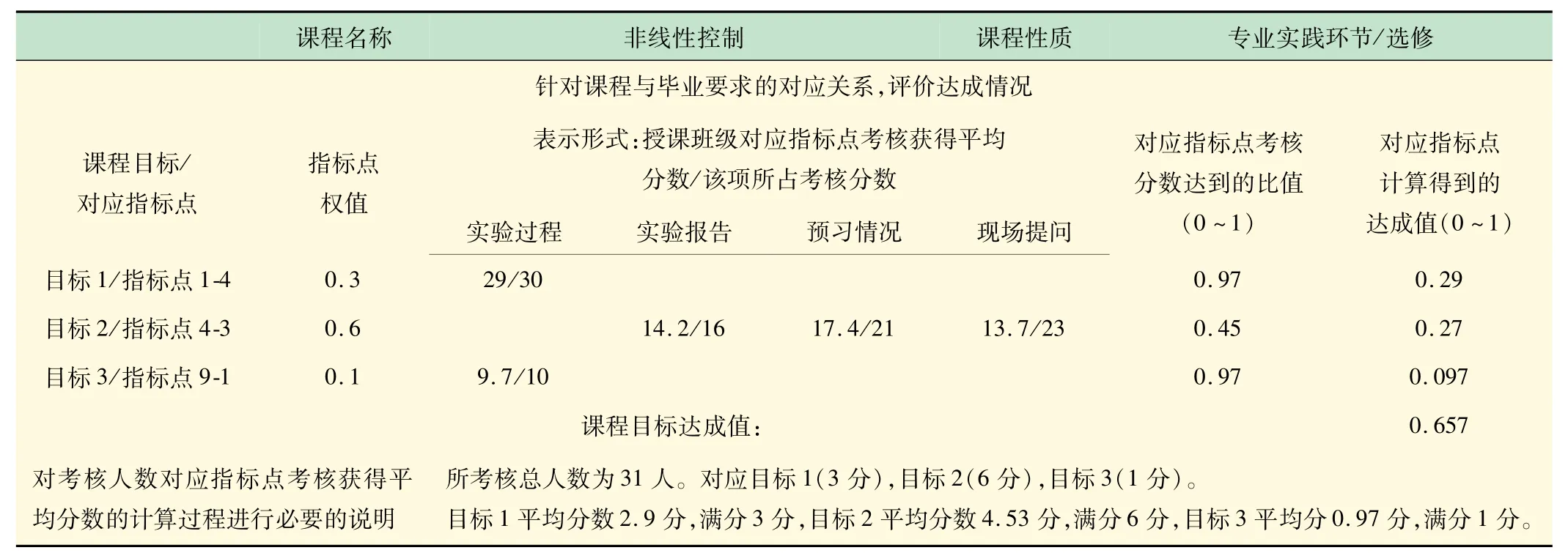
表2 专业课程达成度评价表（成绩定量分析法—授课教师）

目标1掌握现代控制系统设计方法，掌握非线性控制系统的组成及测量元件的选择、被控对象建模、非线性控制器设计等，能够运用所学知识进行实验方案设计、实验方案实施和实验系统搭建；

目标2熟练掌握线性系统设计及稳定条件、掌握Kalman滤波器及应用、神经网络及应用。能够根据非线性控制理论知识对获得的实验数据和观察到的实验现象进行分析和解释，以获得有效结论；

目标3实验中能够明确个人责任，以协作方式完成各实验项目。

指标点1-4掌握智能自动化科学与工程专业基础知识，能够综合运用所学知识分析解决相关领域复杂工程问题；

指标点4-3能够参照理论模型对实验数据进行分析和解释，并得到有效结论；

指标点9-1能够在多学科背景下的团队中承担独立个体的责任。

由表2 知道，目标2 平均分数偏低，原因是有些学生在现场提问＋预习考核方面分数偏低，大部分是在线性系统设计及稳定条件和卡尔曼滤波器这2 个知识点掌握的不太好，说明这些学生没预习或理论基础不扎实。

6 结语

基于问题的探究式学习，达到了实验（实物＋仿真）目的，学生加深理解和掌握了一个复杂控制系统设计过程，熟悉了kalman 滤波器的应用、自适应控制（包括基于数据的非线性建模-神经网络，并且可以给学生拓展利用神经网络预报、故障诊断等功能）等。利用成绩定量分析找到学生实验出现的普遍问题，为后续改进提供依据。