几种典型盲复原算法对光学遥感图像质量提升效果对比分析

林 峰，刘世杰，韩 杰

（同济大学 测绘与地理信息学院，上海 200092）

0 引 言

随着遥感卫星成像传感器的快速发展，图像空间分辨率越来越高。时间延迟积分耦合装置（TDICCD），通过多片CCD 对同一地物进行多次扫描，利用时间延迟积分技术成像，提升了成像传感器的灵敏度和图像的信噪比，这一优势使其成为了成像设备的主流［1］。遥感卫星在飞行过程中受到外界环境（如地球引力、温度等）和内部因素（如姿态控制系统等内部荷载运转）的影响，不可避免地产生颤振，颤振会降低相机姿态的稳定性，使成像姿态随时间发生变化，产生指向角误差，使得TDICCD 成像时，每片CCD 对同一地物成像的像素位置不同，导致CCD 合成后的图像出现模糊［2］。与此同时，卫星的飞行速度和地球自转的速度不相等造成相机和地物出现相对运动，使得图像出现整体性的运动模糊［3］。成像传感器自身的元器件存在物理畸变，也会造成图像模糊。综上，造成遥感图像模糊的原因错综复杂，无法一一区分所有因素对成像的影响。因此，本文从图像的角度出发，研究盲复原方法对遥感图像进行去模糊处理，提升图像辐射质量。

1 相关工作

图像模糊在数学模型上表示为清晰图像与模糊核的卷积再加上一定的噪声。典型的噪声模型有高斯噪声和泊松噪声。当模糊核未知时，从图像模糊到图像清晰的过程称为图像盲复原。在图像盲复原中，已知量只有模糊图像，待求量有潜像、模糊核和噪声，求解过程是病态的。因此，图像先验信息和模糊核模型建立成为图像盲复原中的研究重点［4］。文献［5］中基于规范化稀疏先验，提出了新的盲复原算法，为获得真实清晰的图像仅需要较少的计算量。由于算法的简单高效，使得该算法是快速和鲁棒的。文献［6］对模糊核和图像同时进行组稀疏L1范数正则化，解决了同一场景的多幅模糊图像进行盲复原的问题。文献［7］提出了小支持度正则化反卷积方法，对环境卫星遥感图像进行去模糊，该方法用高斯退化模型拟合复杂原因造成的模糊效应。文献［8］提出了一种有效的基于暗通道先验的盲图像去模糊算法。由于暗通道的稀疏性，引入了线性近似，来解决非凸非线性的优化问题。文献［9］提出了极值通道先验，在复原过程中同时利用了亮通道先验和暗通道先验，该方法较好地复原了合成图像和自然图像。文献［10］结合负对数泊松对数似然法，对图像梯度的L0 范数、潜像和模糊核的L1 范数分别进行正则化。该方法在合成图像和真实图像上，能够获得高质量的复原图像。文献［11］提出了混合梯度稀疏先验约束下的图像盲复原，其中利用图像高阶梯度的稀疏性，并与低阶梯度相结合来构造混合梯度正则项。文献［12］基于维纳滤波和综合评价因子对遥感图像复原。该方法采用维纳滤波复原退化图像，并利用直线运动方法估算图像的退化函数。文献［13］中通过观察文本图像的不同属性，提出了一种基于强度和梯度的L0 正则化先验，该算法可有效地应用于文本图像和低光照图像的去模糊。文献［14］中提出了一种简化的局部最小像素稀疏先验，在最大后验估计框架下，灵活地对局部最小像素进行稀疏诱导，避免了现有算法的非严格逼近，提高了计算效率。文献［15］在最大后验框架下，提出了迭代Lp 范数正则化和数据驱动策略对图像复原。

综上所述，尽管图像复原方法不断发展，然而目前这些先进的方法并没有在遥感图像的应用上进行过对比分析。因此，本文将基于不同先验信息的复原方法，应用于遥感图像，对比分析不同算法的复原效果，为图像辐射质量提升处理的算法选择提供参考。

2 方法

2.1 基于强度和梯度的L0 正则化先验的盲复原法［13］

基于强度和梯度的L0 正则化先验对图像进行去模糊。L0 范数是指约束项中非0 值的个数。复原模型如下：

其中，x为潜像；∇x为潜像梯度；k为模糊核；y为模糊图像。

上式优化表达式中包含两个变量，求解时拆分为x子问题和k子问题。

x子问题：

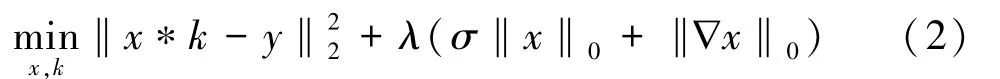
由于L0 正则化具有非凸性，难以直接求解，采用辅助变量u替代x，g替代∇x。求解公式如下：

模糊核估计时，在梯度下求解更为精确，则模糊核求解模型为：

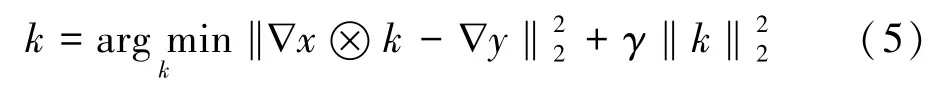
上式为凸函数，则可利用与x子问题求解类似的方法求解，求解公式如下：

2.2 基于学习迭代自适应先验的盲复原法［15］

基于学习迭代自适应先验的盲复原法的复原模型为：

求解公式如下：

其中，K为模糊核k的矩阵形式，w为辅助变量。

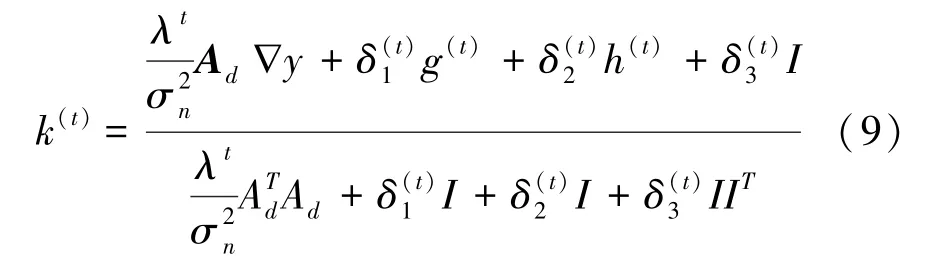
其中，Ad为∇x的矩阵形式；h，g为辅助变量；I为单位矩阵；II为元素全为1 的矩阵。

该方法将广义收缩阈值（GST）算子推广到具有负p值的Lp 范数，通过学习迭代自适应先验获取GST 算子。GST 算子可以提升模糊核估计的精度，以实现动态显著边缘选择和时变正则化。

2.3 基于局部最小强度先验的盲复原法［14］

基于局部最小强度先验的盲复原法的复原模型为：

其中，‖P(x)‖0表示对潜像的稀疏诱导。

求解上式时，首先求解‖P（x）‖0，对遥感图像中的各个图像块最小像素进行稀疏诱导，更新潜像x。步骤如下：

Step 1确定图像块尺寸r，将遥感图像分割成多个图像块；

Step 2确定稀疏诱导的阈值；

Step 3求算每个图像块中的最小像素值，判断其是否小于阈值，若小于阈值，则将该像素值替换为0，否则不变。

上式包含变量模糊核k和潜像x，在优化过程中采用交替迭代优化法。

x子问题：

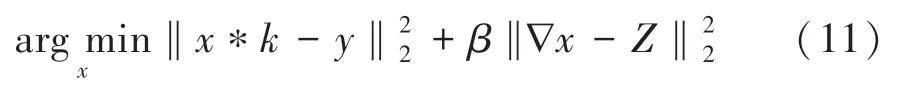
频域求解公式：

k子问题求解同2.1 节中的方法，采用公式（6）求解。k子问题求解之后，使用拉普拉斯先验［16］和L0 正则化先验复原图像［13］得到I1和I2；随后计算两个复原图像之间的差值ΔI，将ΔI进行双边滤波处理得到伪影；最后用I1减去伪影得到复原后的图像。

3 实验

3.1 实验数据

实验数据使用吉林一号高分03A 和03B 微纳卫星的全色波段影像。波段范围为480－700 nm，分辨率1 m。高分03A 影像拍摄时间为2019 年11月，高分03B 影像拍摄时间为2020 年10 月。本文从两景遥感影像中分别截取了两幅1000*1000 像素的影像进行实验。

3.2 实验结果分析

本文分别采用3 种典型盲复原方法，对遥感图像进行去模糊处理。根据文献提供的参考参数，并调整各个参数，对比实验结果，得到不同方法在遥感图像应用上的最优参数设置。具体设置如下：

基于强度和梯度的L0 正则化先验方法的参数设置：λ＝4×10－4，γ＝2，σ＝1；基于学习迭代自适应先验方法，通过学习的方式为图像复原提供先验信息，参数设置：Kernel Size＝27、NoiseSD＝17；基于局部最小强度先验方法的参数设置：μ＝5×10－3、β0＝10－2、βmax＝105、γ＝2、r＝5、σmin＝0.1。图像复原前后的结果对比情况如图1 和图2 所示。

图1 吉林一号高分03A 遥感图像复原前后对比Fig.1 Comparison of remote sensing images of Jilin－1 GF－03A before and after restoration

图2 吉林一号高分03B 遥感图像复原前后对比Fig.2 Comparison of remote sensing images of Jilin－1 GF－03B before and after restoration

由图可见，对于高分03A 遥感图像，基于强度和梯度的L0 正则化先验方法复原的结果含噪声较多，基于学习迭代自适应先验方法复原的结果细节信息较少，而基于局部最小强度先验方法复原的结果包含的细节信息更多、噪声更少，复原效果最佳。对于高分03B 遥感影像，基于学习迭代自适应先验方法复原的结果含有较多噪声，图像更加锐化；基于强度和梯度的L0 正则化先验方法和基于局部最小强度先验方法复原的结果相差较小，都较原始图像更清晰。

为进一步对比分析不同方法的复原效果，本文采用无参考度量线性回归（LR）指标［17］评价不同方法的复原结果。该评价指标用于评价图像复原前后的模糊对比情况，LR值越大，图像更加清晰。评价结果见表1。

表1 吉林一号高分03A、03B 遥感图像辐射质量评价指标复原前后对比Tab.1 Comparison of radiation quality evaluation indexes of Jilin－1 GF－03A and GF－03B remote sensing images before and after restoration

由此表明：对于吉林一号高分03A 遥感影像，基于局部最小强度先验方法复原后图像的LR值最高，复原效果最佳；对于吉林一号高分03B 遥感影像，基于学习迭代自适应先验的复原结果LR值最大。

4 结束语

本文分别采用了基于强度和梯度的L0 正则化先验、学习迭代自适应先验、局部最小强度先验的图像盲复原方法，对吉林一号高分03A、03B 卫星全色波段遥感图像进行去模糊处理。实验结果表明，3 种盲复原方法均能在一定程度上较好地提升遥感图像的辐射质量；对于吉林一号高分03A 遥感影像，采用基于局部最小强度先验的图像盲复原方法复原后的遥感图像较其它两种方法细节信息更多、噪声更少、LR值更高；对于吉林一号高分03B 遥感影像，基于学习迭代自适应先验方法复原的图像LR值更高，图像更加锐化，但产生的噪声较多。