蚂蚁花呗和京东白条的个人信贷风险分析

向玉婷 潘莉

摘 要：近年来网络借贷业务竞争激烈，个人信用贷款的风险控制已无法忽视。因此为帮助金融平台规避个人不良借贷的信用风险，本文以蚂蚁花呗和京东白条为例，运用R软件，通过建立关于还款理想程度的定序回归（probit）模型寻找影响还款状况的显著因素。研究表明，对数平均信用额度（累计信用额度/平台开户数），性别，常住地、网络贷款频率均为显著影响因素。并对该模型的预测准确度进行验证，结果显示：该定序回归模型的精确度可以达到67.69%，但该模型对类1，类2的判断准确率较低。

关键词：个人贷款风险;定序（probit）回归;还款理想程度模型

1研究背景

随着网络金融不断发展壮大，网络借贷作为互联网金融的一部分，因其借贷门槛低，放贷速度快的信用贷款模式成为当前市场上小额贷款的首选方式。当前最受追捧的网络贷款类型当属网络信用贷款，例如蚂蚁集团的蚂蚁花呗、蚂蚁借呗，京东金融的京东白条、金条，度小满金融有钱花等。与传统贷款发展相同，网络小额信用贷款也存在风险控制问题，如逾期还款、不还款、金额套现等。由于很多平台对个人信用的风险把控不严，导致部分资信不良的个人成功借贷，使金融平台遭受损失。本文针对目前互联网金融和个人信用贷款的大背景，欲通过收集用户基础信息与历史借还款状况信息去构建个人信用贷款风险模型，帮助金融平台规避个人不良借贷的信用风险，构建互联网金融借贷的优质客户画像。

2模型构建

2.1数据说明及变量选择

本文数据共涉及1个被解释变量（还款理想程度）和9个解释变量（性别、常住地、学历、收入、是否理财、支出、网络贷款频率、累计信用额度和平台开户数）。

被解释变量（还款理想程度）共分为三个等级：1-还款理想状态-按期最低还款;2-还款较理想状态-按期部分还款（还款金额>最低还款金额）;3-还款不理想状态-按期全还款和逾期还款。

由于被解释变量为定序变量，为深入挖掘影响还款理想程度的影响因素，本文选择Probit定序回归模型进行拟合。

2.2Probit定序回归模型

定序回归与传统的线性模型不同，其因变量为有序的分类变量，比如不合格、合格、优秀等。为了方便分析，定义解释变量为X= （1，X1…，Xp）^'，其中p是解释变量个数，相应的回归系数记作β=（β0，β1…，βp）' ，其中 是截距項。由于因变量Y是一个分类变量，为离散型的定性指标，定序回归模型直接定义为Y= X'β+ε是不合适的，这时考虑潜变量Z，帮助将定序数据模型表达出来：

其中， ci  （i=1，2，3，4）是未知的阈值，Z是一个连续变量，假设Z服从标准正态分布，可以计算出Y在各个取值下的条件概率，此时将等号左边因变量Y映射为[0，1]区间的连续概率值，等式就可以构成如下模型：

k表示不同Y的取值，取值为1，2，3…， 表示截距项，i，j均为正整数。 Ф（.） 代表Probit回归模型。同简单的0-1型Probit回归一样，对定序Probit回归而言，也是采用极大似然准则进行对被解释变量的估计。

在自变量的选取过程中，全模型的构造不会剔除变量，可能会导致模型的自变量过多或存在不显著因素，导致模型精度降低。而AIC准则可以有效防止模型复杂度过高，在保证模型精度的前提下筛选出最优子集，使拟合精度与位置参数个数实现最优化配置。

2.3AIC信息准则（Akaike Information Criterion）

AIC准则是由日本统计学家赤池弘次（Akaike）在1974年提出，AIC全称是最小信息准则（An Information Criterion），它建立在熵的概念之上，是一种考评综合最优配置的指标，是拟合精度和参数未知个数的加权函数：

AIC=-2ln（模型中极大似然函数值）+2*（模型中未知参数个数）

3 AIC准则下模型实证分析

本文运用R语言，分别对全模型和AIC、BIC准则下最优模型进行试算，最终选择AIC准则模型进行分析。

AIC准则下模型运行结果如下：

P（还款理想程度<=1）=Ф（-3.789-0.378*对数支出+0.134*对数均信用额度+0.343*性别2（女）-0.414*常住地2（乡村）-0.174网络贷款频率2（2～3个月）+0.155*网络贷款频率3（半年左右）+0.643*网络贷款频率4（偶尔））       （3.1）

P（还款理想程度<=2）= Ф（-2.228-0.378*对数支出+0.134*对数均信用额度+0.343*性别2（女）-0.414*常住地2（乡村）-0.174网络贷款频率2（2～3个月）+0.155*网络贷款频率3（半年左右）+0.644网络贷款频率4（偶尔））        （3.2）

在5%的显著性水平下，式子（3.1）和（3.2）分别给出了还款理想程度小于等于1及还款理想程度小于等于2的累计概率，由于正态分布函数在定义域内单调递增，因此对式子（3.1）和（3.2）中回归系数作简要的分析如下：

1）. 对数支出：对数支出的参数估计系数为负，说明在给定其他条件相同的情况下，相较于对数支出低的用户来说，对数支出高的用户，其还款理想程度取值偏小，还款状况更理想;

2）. 对数均信用额度：对数均信用额度的参数估计系数为正，说明在给定其他条件相同的情况下，相较于对数均信用额度低的用户来说，对数均信用额度越高，还款理想程度取值偏大，还款状况越不理想;

3）. 性别：性别2（女）的参数估计为正，说明在给定其他条件相同的情况下，相较于男性用户来说，女性的还款理想程度偏大，还款状况更不理想;

4）. 常住地：常住地为乡村的参数估计为负，说明在给定其他条件相同的情况下，相较于常住地为城市用户来说，常住地为乡村用户的还款理想程度偏小，还款状况更理想;

5）. 网络贷款频率：网络贷款频率（偶尔）的参数估计系数为正，说明在给定其他条件相同的情况下，相较于网络贷款频率（每月）的用户来说，网络贷款频率（偶尔）的用户的还款理想程度偏大，还款状况更不理想。在给定其他条件相同的情況下，对于标准组（网络贷款频率—每月），网络贷款频率3（2～3个月）和网络贷款频率4（半年左右）均不显著。

4模型预测

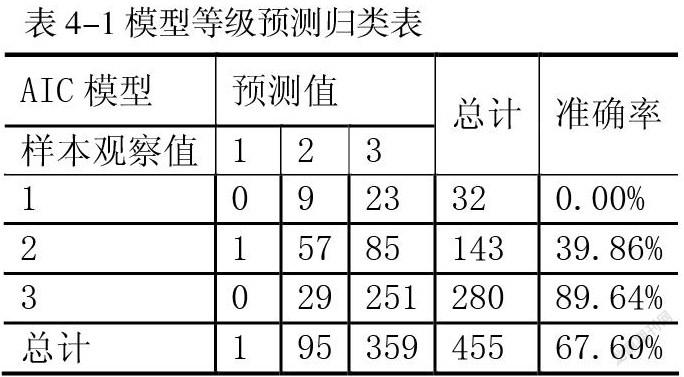
根据模型预测原理，结合R软件输出的概率预测值和混淆矩阵整理得到表4-1：

如表4-1所示，类别1的32个样本中，没有预测正确的，正确率为0.00%;类别2的143个样本中，有57个预测正确，正确率为39.86%;类别3的280个样本中，有251个预测正确，正确率为89.64%;全部455个样本中，有308个预测准确，准确率为67.69%。由此可知，该模型的总预测准确率中等，对类3预测准确性较高，对类1和类2的预测准确性很低。

5结论及展望

对AIC模型解读，发现相较于其他用户，对数支出越高、对数均信用额度越低、男性、网络贷款频率为偶尔的用户的还款状况更理想，平台承担的风险也会更低。同时，通过AIC模型预测结果表明，AIC模型的准确率为67.69%，具有一定的预测能力。预测结果表明，尽管模型AIC对于样本等级判定具有一定的准确率，但该模型对类1和类2的预测准确度很低，模型准确度有待进一步提高。后期可考虑在模型中加入优势比（OR）概念，计算优势比（OR），明确每增加一个单位X，对于Y变化幅度的影响，更好的解读模型。

参考文献：

[1] 陈春香.浅论商业银行个人消费贷款风险管理[J].经济视角，2019（10）：61-63.

[2] 王汉生，成慧敏.商务数据分析与应用——基于R[M].北京：中国人民大学出版社，2020：160-215.

[3] 范欣欣，陈立明，许军.公务员亚健康状况影响因素的有序多分类Logistic回归分析[J].中国卫生统计.2017（05）：770-773.

作者简介：

[1]向玉婷，成都信息工程大学统计学院学生

[2]潘莉，成都信息工程大学统计学院讲师，硕士;研究方向：金融数量分析。