传染病在噪声影响复杂网络上引起的同步

张晓磊，刘茂省

（中北大学 理学院，太原 030051）

如今，许多现实世界的系统可以用复杂动态网络描述，如互联网、神经网络，生物系统。研究并探索复杂网络中出现的不同动态行为之间的相互作用是增强对其理解与运用的有效举措［1］。在不同的动态行为中，网络上个体应对传染病引起的集体行为和传染病传播之间的关系已经引起大多数人的关注。随着传染病的传播，个体会收到来自政府、媒体或人与人之间等其他途径得知的传染病信息来适应性地改变各自的行为，即采取集体行为以避免被感染，如经常用清水洗手，避免去拥挤地方等，以提高自我保护，这意味着在传染病传播的过程中，个体之间有关传染病信息的传播可以自发地诱发集体行为，这表明网络上个体应对传染病引起的集体行为和传染病传播，可以同时发生并自适应地相互作用。

在过去的几年中，复杂动态网络的同步问题受到广泛关注，如在小世界［2］和无标度动态网络［3］中，推导出了动态网络完全同步的准则，其中指出网络拓扑结构和节点动态之间的相互作用对于网络实现完全同步十分重要。就传染病传播过程中的同步研究，李科赞等［4］集中在传染病传播如何影响个体的集体行为方面开展研究，提出了基于异质平均场（HMF）理论的SIS（易感－感染－易感）和SIS（易感－感染－恢复）传染病同步模型，得出传染病的传播会引发个体行为的变化，进而影响传染病的演变。李科赞等［5］研究了在复杂网络上个体行为的同步和传染病传播之间的相互作用，即不仅研究传染病传播对个体行为同步的影响，还研究个体行为同步对传染病传播的影响，更分析了传染病传播的控制问题。孙孟锋等［6］在传染病传播过程中，引入了在个体之间传染病信息传播与传染病传播之间的耦合时滞，构建了3种不同（无时滞、耦合时滞和双重时滞）的数学模型，并分别研究了在复杂网络上个体行为的同步与传染病传播之间的相关性，分析了传染病同步数学模型的局部和全局稳定性。李俊民等［7］研究了具有未知周期时变耦合和随机噪声扰动的复杂动态网络的同步问题，得到了复杂动态网络同步的充分条件。

然而，目前对传染病传播过程中个体行为同步的研究大都是不受噪声影响的复杂网络模型，为了更好地评估复杂网络中传染病传播与个体行为之间的相互作用，研究了在受随机噪声扰动影响的复杂网络上，个体应对传染病引起的集体行为与传染病传播之间存在的相互作用的问题。在受噪声影响复杂网络模型的基础上，应用实际网络中观察到的自适应机制，通过向网络上节点添加合适的控制器，构造传染病同步的数学模型来研究受控噪声影响复杂网络的同步问题。

1 模型的建立

基于文献［5］的复杂网络模型（1），建立具有N个节点组成的受噪声影响复杂网络（4），

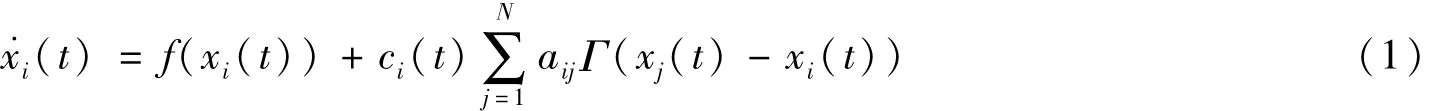
其中xi（t）＝［xi1（t），xi2（t），…，xin（t）］T∈Rn，代表第i个节点在t时刻的状态变量，t∈［0，＋∞），f∶Rn×R→Rn是一个连续非线性向量值函数，描述节点的局部动态；ci（t）＞0表示耦合强度；Γ＝diag（γ1，γ2，…，γn）∈Rn×n代表内部耦合矩阵，是一个正定对角矩阵；A＝（aij）N×N是网络的邻接矩阵，若节点i与节点j（i≠j）之间有连接，则aij＝aji＝1，否则aij＝aji＝0。基于邻接矩阵A，网络的Laplacian矩阵L＝（lij）N×N可表示为

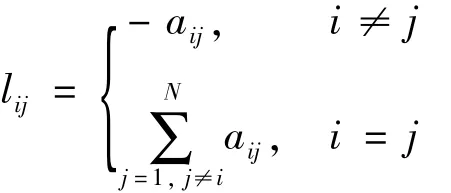
Laplacian矩阵L＝（lij）N×N的对角元素满足以下等式：

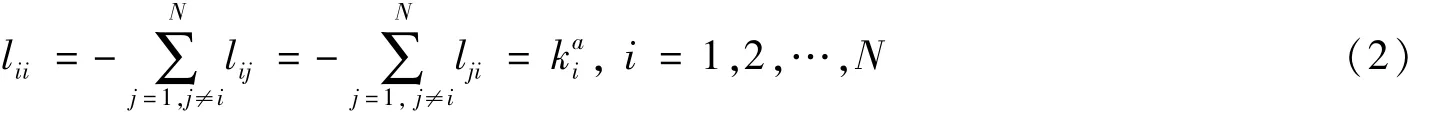
这里kai表示节点i的度。假设L是不可约矩阵，意味网络是强连通，没有孤立集群。根据文献［8］可知0是L矩阵的重数为1的最小特征值，并且其他特征值都严格为正。

复杂网络模型（1）可用Laplacian矩阵表示为

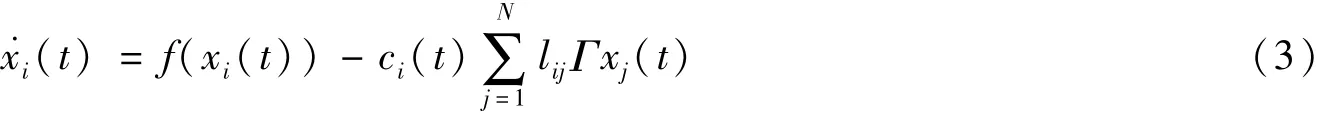
具有N个节点组成的受噪声影响复杂网络，如下所示：

对于（4）与（1）（3）相比，除多了最后一项gi（x1，x2，…，xN）dωi（t）以外，其他符号表示一致，其中gi∈C（Rn×… ×Rn，Rn×n）是噪声强度函数矩阵，ωi（t）＝（ωi1，ωi2，…，ωin）T∈Rn是n维向量Wiener过程，当i≠j时，假设 ωi（t）和 ωj（t）是相互独立的过程。

对于一个孤立节点的解s（t）满足

由于传染病的信息传递具有时滞或其他特殊原因导致传染病暴发时，人们不能在短时间内对其做出相应的反应，此时，对人们的行为进行一些指导，包括在医院获得治疗和隔离，或经常洗手和休息等，以达到抑止传染病爆发的目的。这种行为的指导都可在反馈控制器下实现，本文中，通过在每个节点上增加一个反馈控制器ui（t）来控制个体的行为，以便传染病在网络中传播期间实现所期望的行为同步。受控噪声影响复杂网络描述如下：

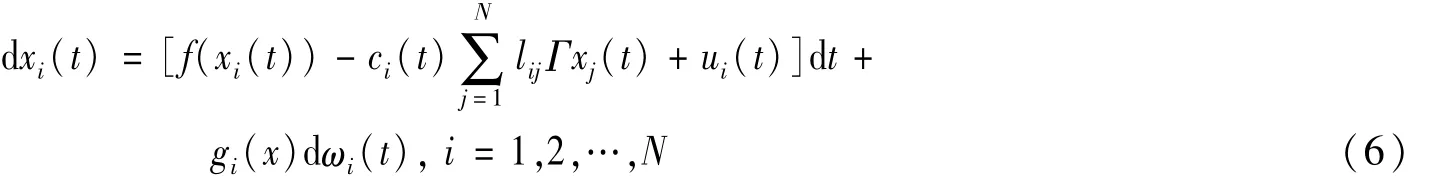
如果对于任何给定的初始状态向量xi（0），受控噪声影响复杂动态网络（4）的解满足以下条件，则称其在均方意义下实现渐近同步，

SIS模型是一种典型的传染病传播模型，在这种传染病传播模型中每个节点处于易感或感染这2种状态中的一种。感染节点以单位速率恢复为易感节点，易感节点以感染率为λ被其邻居感染，变为感染节点。考虑复杂网络上标准SIS模型，其中ρk（t）表示在t时刻度为k的感染节点的密度，则度为k的节点的演化方程可描述为

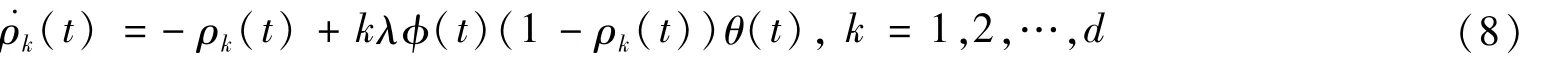
这里θ（t）为从一节点出发与其他节点随机连边，与感染节点相连的概率表易感节点连接到感染节点，它被感染的概率。在实际中个体会根据传染病信息适应性地改变各自的行为（减少个体间接触的频率，并更经常地采取集体保护措施）以避免被感染，因此这样会导致感染率变化，用 （t）来量化这种影响，感染率λ变为λ （t）。对于个体根据传染病信息适应性地改变各自的行为以避免被感染的情况，可以看作是个体受到同步信息（即当传染病传播开来，政府、媒体发出公示或个体互相交流信息：如果采取某种行为可以预防或减少被感染的风险）进而采取同步行为的影响，同时 （t）＝（1－α）E（t）＋α，α∈（0，1）也可看作是准入率［9］，作为同步的信息，可以被认为是个人意识（或风险认知），即如果一个人在公共场合做出同步行为来达到感染控制的目的，这时由于一个人的反应有一种集体化，就可能会使这种同步行为更容易被接受，进而有更多的人去效仿，最终有利于感染得到控制，在整个过程中体现了个体由于受到同步的信息影响进而引起行为的同步。所有个体实现同步时，t→∞，E（t）→0，准入率 （t）达到最小值α。参数α值越小，相对应感染率λ （t）则变小，说明对集体行为的感知程度越高，当α＝1表示传染病传播不会受到同步的影响。

在制定具体的传染病同步模型之前，做出以下基本假设［4－5］：

1）当传染病开始传播时，动态网络中的个体之间存在弱线性耦合；

3）当集体保护行为显著增加时，个人之间的保护信息交流将因达成保护协议而变得饱和。因此，耦合强度变化同步间的比例关系始终保持有效。

在以上假设的基础上，用模型（8）描述传染病传播的特征，用模型（6）描述传染病传播过程中个体保护行为的演化过程，然后可以构造如下SIS传染病同步模型：

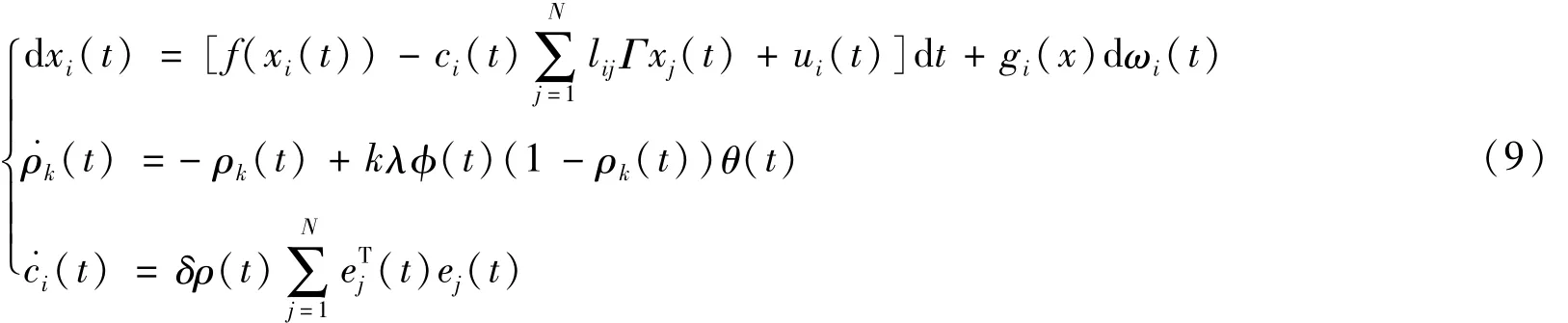
2 受噪声影响的复杂网络上传染病同步的稳定性

定义1 系统（9）的同步流形可定义为

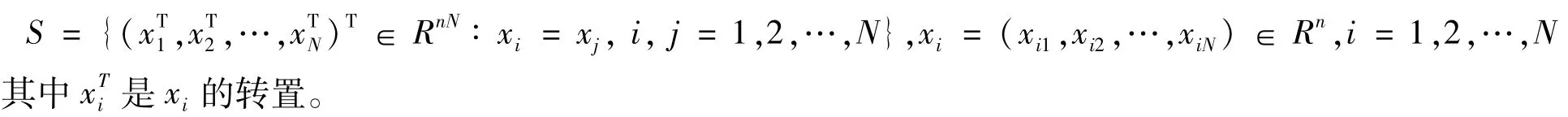
设Ω＝｛（S1，ρ1，…，Sd，ρd）∈R2d＋0≤Sk≤1，Sk＋ρk＝1，k＝1，…，d｝，Ω为系统（8）是正不变集，Ω0在Ω的内部。

从上式可以看出θ＝0是该方程的一个平凡解，下面导出该方程存在正解0＜θ＜1的条件，为了分析θ（t）的性质，构造辅助函数F（θ）：

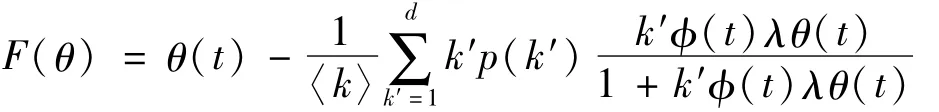
经计算可以得到，

从R0的推导可知当R0＞1，则传染病模型（8）存来，将考虑无病平衡点E0的全局稳定性。

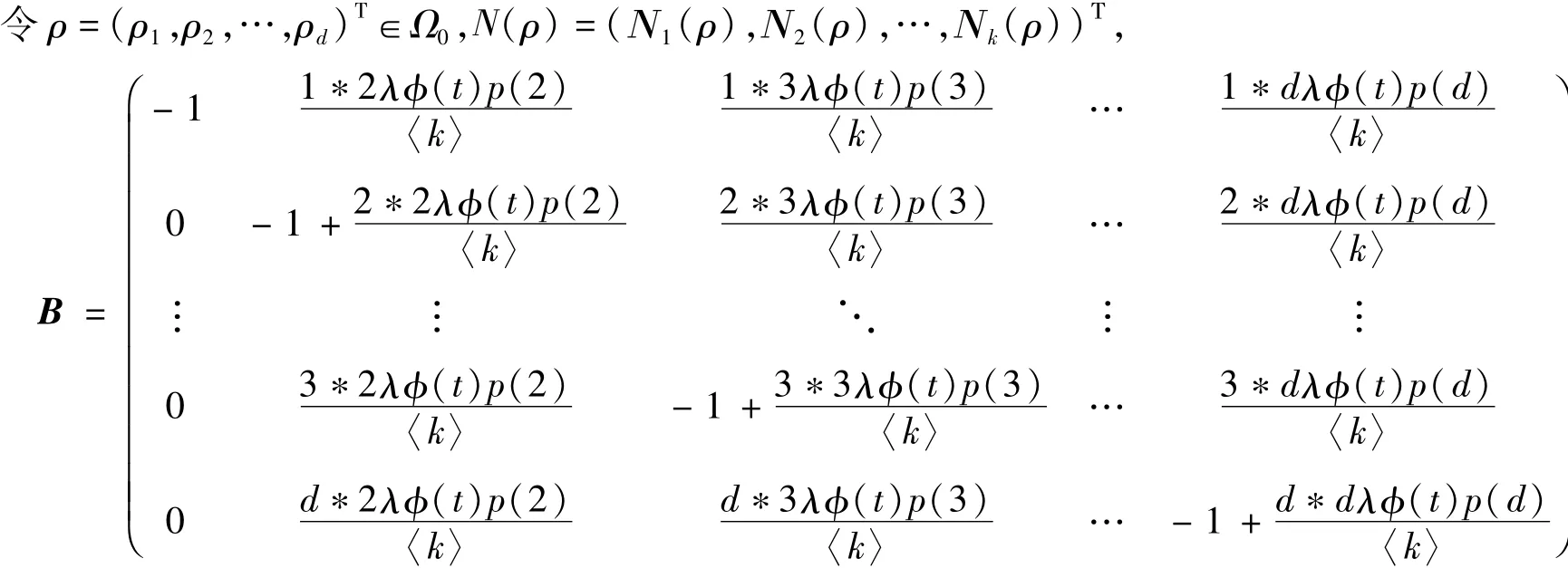
其中Nk（ρ）＝－kλ （t）ρk（t）θ（t），则传染病模型（8）可写为： ρ＝Bρ＋N（ρ），

令B＝－I＋珟B，I表示单位矩阵，

已知Ω为传染病模（8）是正不变集，且Ω0在Ω的内部，所以只需要考虑解在Ω0的全局渐近稳定，对传染病模（8）的两边同时乘以kp（k），并求和得：

构造Lyapunov函数

沿着传染病模型（8）求导，得

为得到定理2，接下来给出以下数学预备知识。

假设1 在受噪声影响复杂网（4）中，假设存在li＞0，满足

假设2 存在非负常数rij，i，j∈1，2，…，N，使得

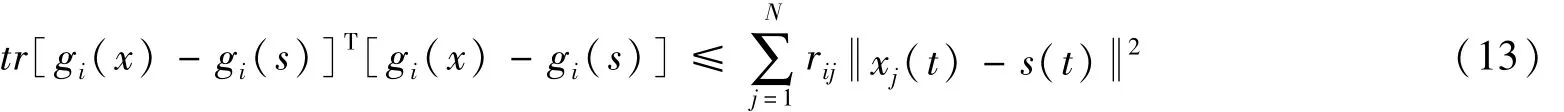
定义2 （It formula）对于n维随机微分系统

V（x（t），t）∈C2，1（Rn×R＋；R＋），这里C2，1（Rn×R＋；R＋）表示所有非负函数的簇，它们关于x是2次连续可微的，关于t是一次可微的。算子LV（x（t），t）被定义为

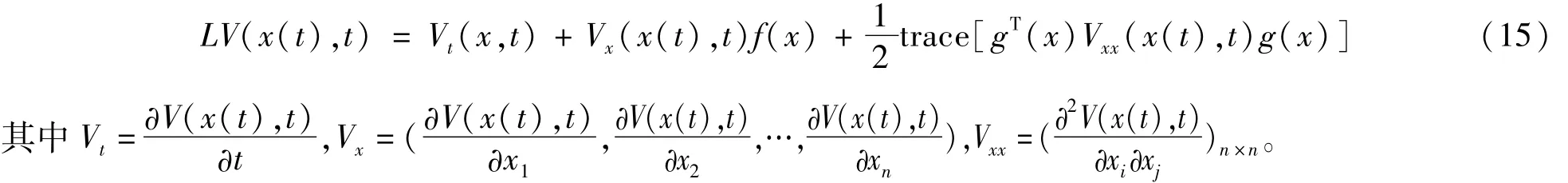
引理1［11］考虑系统（14）设q1、q2、q3为正数，假设存在函数C2，1（Rn×R＋；R＋），使得

那么平衡点x＝0在均方意义下是全局随机渐近稳定的。此外，对于任何∞＞t＞t0≥0，只要积分的期望值存在，则有

考虑受噪声影响复杂网络（4）的同步，为了实现同步目标（7），每个节点上增加的自适应控制器ui（t），（ki（t）是自适应参数）如下所示：

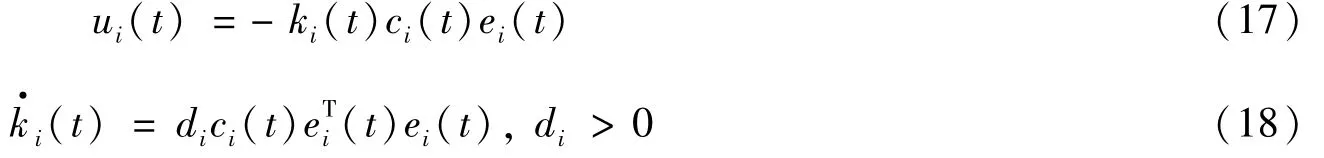
将控制器（17）应用于（6），通过ei（t）＝xi（t）－s（t），则受控噪声影响复杂网络的误差系统可表示为

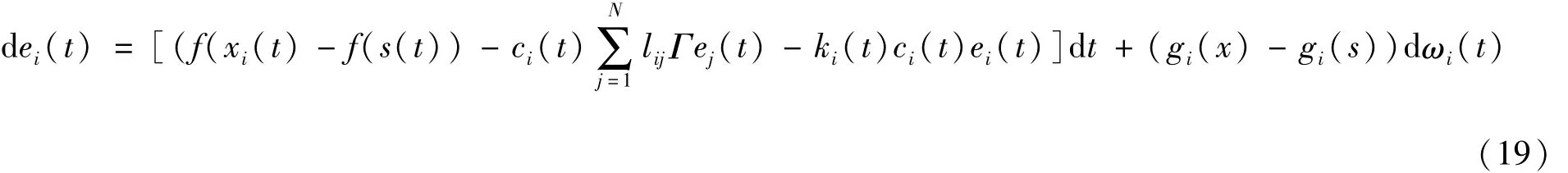
以下定理描述了受控网络（6）全局渐近同步的一个充分条件。

定理2 当R0＞1，传染病模型（8）的地方病平衡点E ，它在Ω0内是全局渐近稳定的，在假设1、2下系统（4），通过控制器（17）和自适应律（18）可保证受控网络（6）在均方意义下全局渐近同步，也就是传染病同步模型（9）的动态行为网络的同步流形是全局渐近稳定的。

证明：因为Si（t）＋ρi（t）＝1，i＝1，2，…，d，则传染病模型（8）可表示为

定义如下矩阵：

对于V1（t），沿系统（8）的解对t求导，相似的分析过程可参考文献［13］，可以得到对于函数V1（t）＝

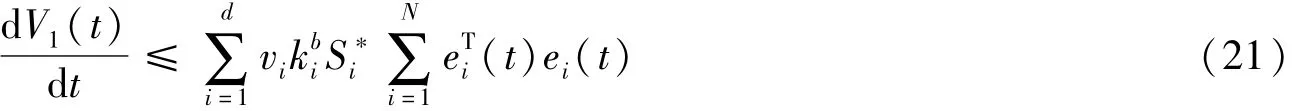
对于

从上两式和假设1、2下，可得

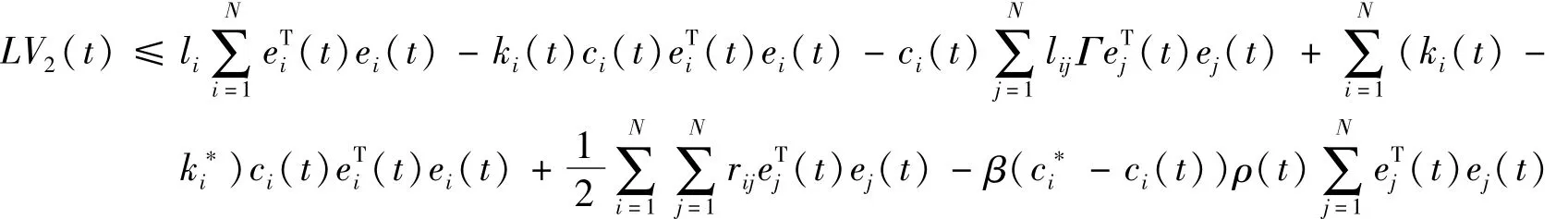
从引理1和式（24），可知

根据引理1，可知误差动态系统（19）在均方意义下是全局渐近稳定的，网络（4）在均方意义下实现渐近同步。

同步流形S也是全局渐近稳定的。

3 数值模拟

为了验证上述结果，对SIS传染病同步模型（9）进行数值研究，嵌入模型（9）中的网络被看成大小为N＝200的BA无标度（优先连接）网络，这个网络是从m0＝4的初始网络演变而来的，我们给每一个新节点添加m＝3新边。不失一般性，假设模型（9）中的f为混沌洛伦兹振荡，尽管从实际传染病传播过程的角度来看，这一假设很难证明是正确的，只是将其用于数值模拟。这种振荡可以描述为

在这里a1＝10，a2＝28，a3＝8／3，Γ看作是单位矩阵，其他参数为 δ＝0．001，α＝0．5，di＝0．01。噪声强度函数矩阵gi（x）＝diag（xi1－xi＋1，1，xi2－xi＋1，2，xi3－xi＋1，3），其中xN＋1，3＝x11，i＝1，…，N。xi的状态初值是从服从均匀分布的［0，1］中随机选取的，初始耦合强度为ci＝0．001，初始感染密度为 ρ1＝ρ2＝0．01，ρi＝0，i＝1，…，d，初始自适应参数为ki＝di＝0．01。

图1中（a）、（b）表示模型（9）的 λ分别等于0．2，0．8时，同步误差E（t），感染密度 ρ（t）和耦合强度

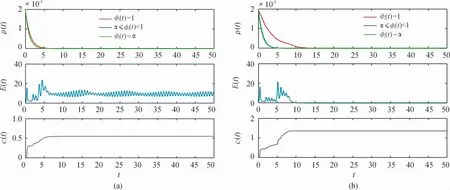
图1 同步误差E（t），感染密度 ρ（t），耦合强度ci（t）分别在 λ＝0．2，0．8时的变化

从图1（a）可知：当λ＝0．2时，传染病不会爆发，没有形成地方病，此时E（t）不等于0，意味着同步没有实现，个体没有表现出集体行为，但是从图上可以看出当传播过程中， （t）满足以下条件α≤ （t）＜1， （t）＝α时，个体之间存在同步信息，此时传染病感染密度收敛为0的速度比 （t）＝1时个体之间不存在同步信息要快，说明个体之间同步信息的存在会加速传染病的灭绝。从图1（b）可知：当λ＝0．8时， （t）＝1传染病感染密度曲线表明个体之间由于不存在同步信息传染病会爆发，但是由于模型中存在自适应控制器导致传染病生成的规模不是很明显，但此时可以明显看到个体之间存在同步信息，传染病感染密度收敛为0，同时E（t）等于0，意味着同步实现，同步信息的存在会使个体表现出集体行为，说明个体的集体行为可以抑制流行病传播行为，反之，这种流行病传播行为可以加速个体的集体行为。

图2是当λ＝0．8时，自适应控制器ui的变化曲线和自适应参数ki的变化曲线。

图3 （a）、（b）表示模型（9）的 λ分别等于1．2，2时，同步误差E（t），感染密度 ρ（t）和耦合强度ci（t）的变化。

从图3（a）可知：当λ＝1．2时，由于模型中存在自适应控制器ui的原因导致传染病生成的规模不明显，从图3（b）可知：当λ＝2时，尽管模型中存在自适应控制器ui，若个体之间不存在同步信息，传染病会爆发，说明模型中的自适应控制器只在感染率在一定范围内才有效，但此时可以明显看到若个体之间存在同步信息，传染病感染密度收敛为0，同时E（t）等于0，意味着同步实现，同步信息的存在会使个体表现出集体行为，从而抑制传染病的传播。

4 结论

研究了受噪声影响复杂网络上由传染病动力学引起的个体同步行为，构建了能刻画这类现象的传染病同步数学模型，研究了模型的感染率与同步稳定性之间的关系，得到了同步模型的全局稳定性条件。数值模拟结果表明：集体行为可以抑制传染病的传播行为，反之，这种传染病的传播行为可以加速集体行为，这一结论与实际复杂网络上传染病的传播特征吻合。因此，在研究复杂网络上的传染病同步问题时，本研究可为更好地理解和控制这类复杂网络系统提供基本框架。