基于MOOC数据的学习行为分析与成绩预测

陶利莎 马燕 爨力源 邹富源 田媛 黄洪琳

摘要：近年来，线上教育的迅速发展给教育者提供了数据化的学习情况反馈，利用这些学习情况的反馈对学生进行成绩预测便是一个新兴研究点。该文记录了研究过程中对学习者行为数据集的分析，对数据进行处理，利用Matlab进行聚类分析等方法进行分析并得出结论。利用数据分析的方法预测学习者成绩在教育者的工作上有着很大帮助。

关键词：数据处理;成绩预测;聚类分析;学习行为

中图分类号：TP399        文献标识码：A

文章编号：1009-3044（2021）35-0027-03

Analysis of Learning Behavior and Performance Prediction Based on MOOC Data

TAO Li-sha， MA Yan， CUAN Li-yuan， ZOU Fu-yuan， TIAN Yuan， HUANG Hong-lin

（The College of Information， Mechanical and Electrical Engineering， Shanghai Normal University， Shanghai 200234， China）

Abstract： In recent years， the rapid development of online courses has provided educators with data-based feedback on study situations. An emerging research focus is to use the feedback of these learning situations to predict the performance of the students. This paper records the analysis of the learner's behavior data set during the research process， processes the data， and uses Matlab to perform cluster analysis and other methods to analyze and draw conclusions. Using the method of data analysis to predict learners' performance is of great help to the work of educators.

Key words： data processing; performance prediction; cluster analysis; learning behavior

在全球化的大背景下，在线学习领域的全球化趋势也越来越显著。特别是由于疫情的原因，线上教育越来越普遍。随着互联网 Web2.0和云计算等技术越来越成熟，大型网络教育平台——慕课 （massive open online course ，MOOC）也正在快速兴起，由于互联网技术的记忆功能，学习者在慕课平台上的所有学习活动和行为都会被以多种形式的数据形式记录下来[1]，基于数据挖掘和机器学习对学习者行为进行建模，分析慕课的发展趋势和优化方案，吸引着越来越多研究人员的参与其中[2]。

由于慕课出现的时间还很短，目前为数不多的研究大致包括关于单维度数据的统计分析、对不同学科、不同线上学习平台数据的综合分析和研究学习者的退出率、论坛的活跃程度、课程完成率等模型[3]。本文在借鉴为数不多的模型，对学习者的学习行为数据进行分析。基于不同的分类模型，建立了预测学习者是否能获得证书和预测学习者成绩的模型，可为慕课课程的教学改进提供借鉴。

1开发思路

利用教育数据分析和挖掘技术，通过大量数据驱动的方式构建在线学习者学业成绩预测模型是目前课题研究的热点。然而，采用人工神经网络、决策树等算法训练的单一预测模型的性能不稳定，由于数据变化导致预测结果误差较大。

对MOOC学习者行为数据分析发现，学习者行为数据分布较为散乱，且成绩分布在低分段的学习者较多。经统计分析发现，与传统的教学模式相比，慕课学习者的学习目标和知识背景分布多种多样，学习者利用平台的方式也各不相同 ，大多数学习者并不是为了获得证书而去学习。仅仅根据选择相关性较强的特征向量对学习者成绩进行预测无法得到较好的预测效果，因而基于学习者的多样性将学习者聚类分析归为不同的类别[4]，再对每类进行线性回归分析得到线性回归方程，最后将测试集代入到预测模型中进行回归方程的显著性检验、拟合优度检验和回归系数的显著性检验[5]用于实际问题中。

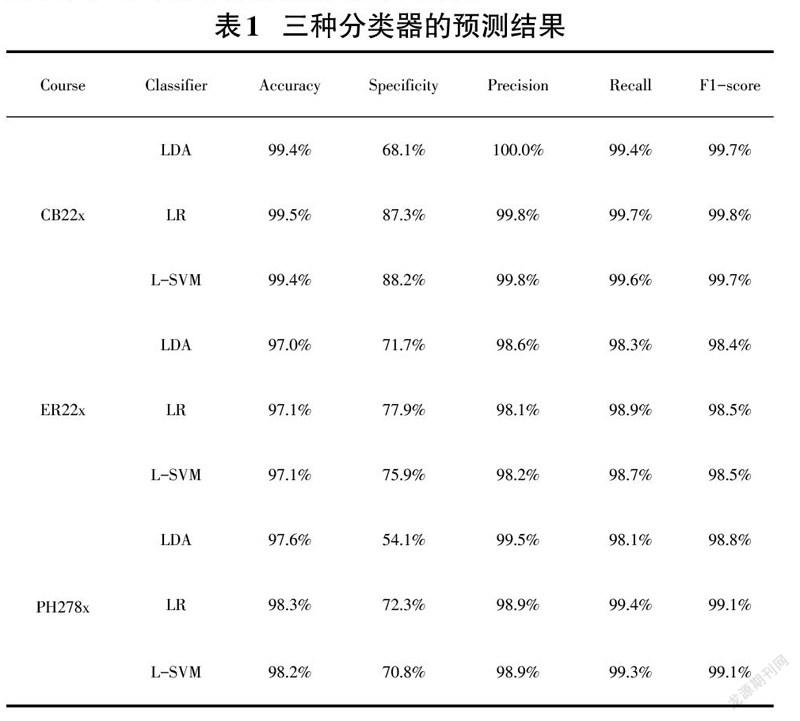
此外，能否获得证书也是平台效用的一个重要体现，本文筛选重要影响变量，采用3种二元分类模型 ：线性判别分析（linear discriminant analysis ，LDA ）、逻辑回归 （logistic regression ，LR）和线性核支持向量机（linear support vector machine ，l-SVM），进行是否能获得证书的预测，准确率均较高。

2预测模型的介绍

2.1用于预测是否获得证书的模型

预测是否获得证书属于典型的二分类问题，本文采用三种适用于该问题的分类模型。

2.1.1线性判别分析

线性判别分析，也称作Fisher线性判别，是模式识别的经典算法。LDA的基本思想是想办法将样本数据投影到一条合适的直线上，使投影到直線上的同类样本之间差异尽可能的小，使不同类样本间的差异尽可能的大，这样就可以直观且简便地判断某个样本数据属于哪一类了。使用该种方法可以使投影后的模式样本在新的空间中有最小的类内距离和最大的类间距离，即模式在空间中拥有最佳的可分离性。因此，它是一种有效的特征提取方法，采用该方法也能将学习者进行准确地分类。

2.1.2逻辑回归

逻辑回归模型是针对二分类问题的一种易于实现而且性能优异的分类模型。逻辑回归目的是从特征学习出一个0/1分类模型，其中，用1表示获得证书，0则反之。这个模型是将特性的线性组合作为自变量，即选择学习者的特征向量数据作为自变量，由于自变量的取值范围是负无穷到正无穷。因此，使用logistic函数（或称作sigmoid函数）将自变量映射到（0，1）上，映射后的值被认为是属于y=1的概率，也就是获得证书的概率。然后将映射后的值在（0.5，1）的归为一类，将处于（0，0.5）的归为另一类，便完成了学习者的分类。

2.1.3线性核支持向量机

支持向量机（SVM）是一种监督式学习的方法，它广泛地应用于统计分类以及回归分析中，同样也是解决分类问题的经典模型。考虑到学习者的特征向量数据是非线性的，本文的处理方法是选择线性核函数，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。在分开数据的超平面的两边建有两个互相平行的超平面，分隔超平面使两个平行超平面的距离最大化，可以对数据进行有效地划分。

2.2用于预测成绩的模型

2.2.1K-means聚类模型

聚类和回归是两类主要的预测问题，聚类是预测离散的值，形成的离散的“簇”对应着潜在的离散概念的划分。回归是预测连续的值，将两者进行结合能得到适应性较强的预测模型。对于无标签的学习者样本，采取无监督的K-means聚类分析对学习者进行划分，这种方法的主要缺点是随机选择初始质心，如果数据存在离群值，可能会收敛到一个不稳定的结果，采用LOF算法剔除离群值可以提高模型的准确率。

实现K-means算法主要包括以下四点：

（1）簇个数 k 的选择;

（2）各个样本点到“簇中心”的距离;

（3）根据新划分的簇，更新“簇中心”;

（4）重复上述2、3过程，直至"簇中心"不再移动。

2.2.2线性回归模型

主要包括以下几个步骤：

（1）对K-means聚类后的各数据点求取线性回归方程;

（2）测试集检验，将测试数据点归到距“簇中心”距离最小的一类;

（3）代入该类的线性回归方程中，得到预测值;

（4）方程通过回归方程的拟合优度检验[5]，评估预测模型确定最优回归模型。

3具体实现

本文利用matlab及其工具箱进行应用程序的编写，建立了一个分类预测模型，对在线学习的学习者是否获得证书和学习成绩进行预测。

3.1学习者是否获得证书的预测

首先，导入与获得证书相关的两个特征向量数据：页面访问量和学习章节数。对数据进行异常值的剔除：

for i = 1：m

for j = 1：m

dist（i，j） = norm（K_train（i，：）-K_train（j，：））;

end

end

lof = LOF（dist）;

for i=1：m

if lof（i）>1

K_train（i，：）=NaN;

end

end

K_train = K_train（all（～isnan（K_train），2），：）;

其次，對数据进行归一化处理，归一化代码如下：

[x，y]=size（data）;

tackledata=zeros（x，y）;

maxd=max（data）;

for i=1：y

for j=1：x

tackledata（j，i）=data（j，i）/maxd（i）;

end

end

调用matlab的classification learner工具箱，选择线性判别、逻辑回归和线性支持向量机进行训练。

其中，将模型导出后，可以通过如下语句检验模型：

trainModel.predictFcn（data）;

3.2学习者成绩的预测

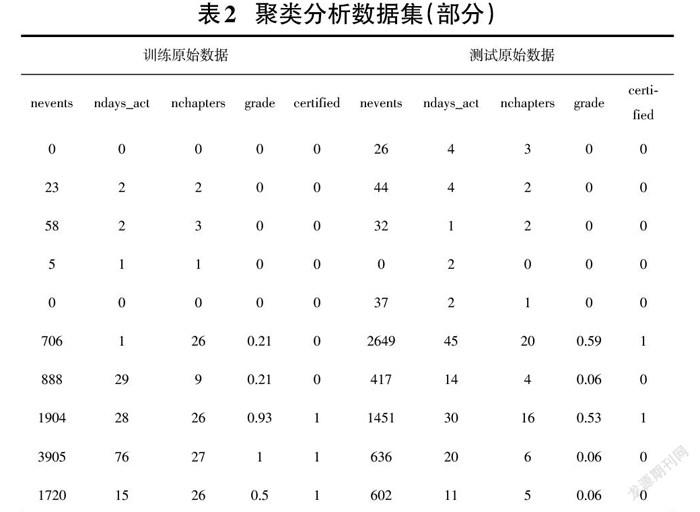
首先，导入与学习者成绩相关的三个特征向量数据：页面访问量、参与课程互动的天数和学习章节数。对数据进行异常值的剔除和归一化处理。

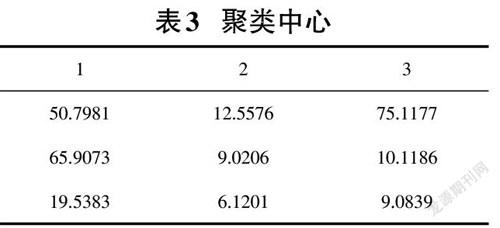
其次，对数据进行K-means聚类分析，得到如表3所示的聚类中心，关键语句如下：

k=3; [cluster2，C，sumD，D]=kmeans（K_train（1：3），k，'Start'，'uniform'，'Distance'，'sqEuclidean'，'Replicates'，5）;

再通过如下代码：

CoeMatrix=[];

for i=1：k

[m，n]=size（K_train（cluster==i，1：3））;

linear = fitlm（K_train（cluster==i，1：3），K_train（cluster==i，4））;

CoeMatrix=[CoeMatrix linear.CoefficientCovariance（：，1）];

end

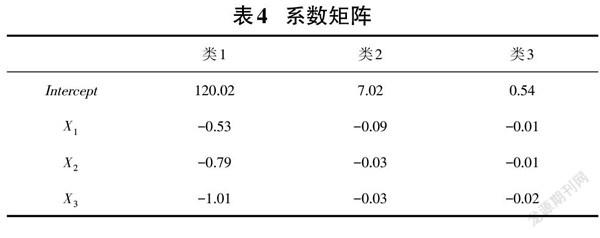
得到各类的线性回归模型，其中，CoeMatrix为三类学习者特征向量的系数矩阵，如表4所示。

结果表达式：

[Y1=120.02-0.53X1-0.79X2-1.01X3]

[Y2=7.02-0.09X1-0.03X2-0.03X3]

[Y3=0.54-0.01X1-0.01X2-0.02X3]

最后，导入测试数据对模型的预测效果进行检验，代码如下：

[Error1，Predition1，clunum]=prediction（CoeMatrix，K_test，C，k）;

[allx，ally]=size（K_test）;

grade=K_test（：，4）;

MSE = sum（（Predition1-grade）.^2）./allx;

RMSE = sqrt（mean（（Predition1-grade）.^2））;

MAE = mean（abs（Predition1-grade））;

R2 = 1 - （sum（（Predition1-grade）.^2） / sum（（grade - mean（grade））.^2））;

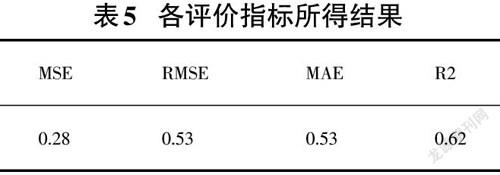
其中，调用prediction函数，可以将测试数据划分到不同的类同时得到预测值和误差，MSE、RMSE、MAE、R2为线性回归模型的评价指标。这是该模型最核心的代码，其余代码在此不做过多赘述。

决定系数R2越趋近于1表明拟合效果越好[5]，实验所得的R2为0.62，说明该模型具有较好的拟合效果。

4 结束语

在宏观方面运用K-means聚类然后进行多元线性回归分析，构建出一种适应性更强的成绩预测模型，微观方面依据判定系数 R2 和估计标准差来检验[5]，具有不错的实际应用效果，可以将需要进行预测的学习者学习行为数据导入，得到相应的预测值。预测结果为教师和管理者对教学计划和教学模式的改进提供了可靠的数据保障，为后续学习行为分析及成绩预测起到借鉴和促进作用。

参考文献：

[1] Breslow L，Pritchard D，DeBoer J，et al.Studying learning in the worldwide classroom：Research into edX’s first MOOC[J].Research & Practice in Assessment，2013，8（1）：13-25.

[2] Waldrop M M. Online learning：Campus 2.0[J].Nature，2013，495（7440）：160-163

[3] 蔣卓轩，张岩，李晓明.基于MOOC数据的学习行为分析与预测[J]. 计算机研究与发展，2015，52（3）：614-628.

[4] 张强. MOOC 学习者学习行为聚类分析[J].通化师范学院学报，2015，36（2）：37-39.

[5] 郝巧龙，魏振钢，林喜军. MOOC学习行为分析及成绩预测方法研究[J].电子技术与软件工程2016（7）：167-168.

【通联编辑：王力】