考虑多公差耦合的几何要素误差建模及产品装配精度预测

刘玉鑫,张根保,冉 琰

(重庆大学 机械传动国家重点实验室,重庆400044)

零件的加工误差是导致装配误差的重要因素之一,也是制造阶段中无法避免的误差,因此,建立零件几何要素的误差模型,是求解装配精度的重要前提,几何要素误差建模主要包括公差带的描述与变动后的几何要素的描述[1]。最早的公差表达模型是Requicha[2]提出了基于变动簇的实体漂移法,漂移实质上是在保持实体外形不变的情况下的拓扑变换,允许漂移的区域即为公差区域。在实体漂移模型的基础上,Jayaraman[3-4]发展完善了漂移理论,提出了一种虚拟边界要求的模型,提高了漂移理论的实用性。Bourdet等[5]在特征恒定度以及TTRS的基础上提出了SDT(small displacement torsor)模型,该模型用于表示几何要素由于公差引起的位置和方向变动。Roy[6-7]、刘玉生等[8-12]在SDT模型基础上通过对常见几何要素的自由度分析,建立了尺寸公差、定向公差、定位公差和形状公差的数学模型,并给出了几何要素各误差旋量参数之间的约束关系,提高了公差分析的精度,使公差建模理论的发展向前推进了一大步。唐水龙等[13]通过构建虚拟平面进行了尺寸公差与平面度公差的耦合作用下的几何要素的误差变动分析;吕程等[14]完善了几何要素在各类公差耦合作用下的误差变动数学表达。

上述研究大多针对某一类公差进行误差建模和讨论,缺少对多公差作用下误差建模的系统研究。现有的多公差作用下的误差建模常采用蒙特卡洛法建立几何要素实际变动与公差之间的关系,其求解过程复杂,故文中提出了一种在公差耦合作用下的几何要素误差建模方法,利用约束方程的不合格率p,更为简便地推导出了各个误差分量参数的实际分布规律,建立几何要素误差模型。基于雅可比旋量模型将该方法扩展应用于复杂装配体的装配误差建模中,实现了装配精度的预测,并结合可靠性理论提出了通过装配精度可靠度来评价装配精度指标,即可用概率来评价装配体满足精度要求的能力,更符合实际生产情况。

1 基于SDT平动公差与固定公差耦合作用下几何要素的误差建模

几何要素误差建模主要需要解决以下2个方面问题:①公差带的形成及表达。公差带是由一个或几个理想的几何线或面所限定的、由线性公差值表示其大小的区域,用来描述允许几何要素尺寸、形状及位置变动的范围。②变动后的几何要素的形成与表示。几何要素在公差带内发生变动后,其尺寸、位置及形状均会发生变化,不是以前的理想状态,因此存在着如何描述变动后几何要素的问题,即如何使变动后的几何要素上表达出公差的效果。本节将采用小位移旋量SDT以理想平面为参考,描述各类公差带以及变动后的几何要素,具体分析过程如下。

1.1 公差带的基本属性与分类

公差带是产品在设计阶段,设计人员给予产品实际尺寸、形状及位置的变动范围,也是产品制造及检测的依据。几何要素的公差带具有形状、大小、方向和位置四个要素,可以根据公差带的方向和位置是否确定来对公差进行分类,具体可以分为3类[8]:公差带固定的公差、公差带平动的公差和公差带浮动的公差,如表1。其中固定的公差带不仅可以控制几何要素对基准的位置变动,还能控制其对基准的方向变动,故如要控制几何要素对基准方向变动,其平动的公差带应小于该几何要素固定的公差带,同理,如要控制几何要素的形状,浮动的公差带应小于该几何要素平动的公差带。

表1 公差的分类Table 1 Classification of tolerances

1.2 基于SDT公差耦合作用下几何要素的误差建模

在SDT公差模型中,将零件实际几何要素的误差通过公称表面的一种微小的刚性变动来表示,并用理想几何要素来代替实际零件实际几何要素[15],小位移旋量可以描述几何要素六个自由度的微小变动,可表示为D=(α,β,γ,u,v,w),其中α、β、γ代表着绕着x、y、z轴旋转的微小转动量,u、v、w代表着沿着x、y、z轴平动的微小移动量。在文中研究范围内,SDT各个变动量是用来描述零件几何要素的误差,故后文也将SDT各个变动量称为误差分量。

由1.1节可知,几何要素误差受多项公差控制时,其的位置分量由固定公差控制,方向由平动公差控制。由于浮动公差不能控制几何要素位置和方向,对SDT各个变动量没有约束作用,故SDT模型对浮动的公差的表示还不够完善,且浮动的公差对装配体的误差累积作用相对较小,故文中仅对固定公差和平动公差进行耦合建模,浮动的公差建模的详细内容见参考文献[16]。

鉴于平面几何要素在实际工程中应用较为广泛,文中将重点讨论平面在固定公差和平动公差耦合作用下的几何要素SDT建模。其中,约束平面的平动公差有平行度、垂直度和倾斜度,固定公差有定位尺寸公差、位置度和对称度,下面以平面定位尺寸公差与平面度公差的耦合作用为例,对几何要素的误差变动情况进行分析,建立多公差耦合作用下的平面公差带。

如图1所示,长b,宽a的平面,以理想矩形平面的几何中心为坐标系原点,坐标系法线方向为Z轴,建立坐标系。TD表示平面的定位尺寸公差带,其方向平行于基准平面,位置距离于基准L处。Tp表示平面的平行度公差带,其方向平行于基准平面,位置不确定。定位尺寸公差与平行度公差耦合作用下的公差带取两个公差带的交集,根据产品几何技术规范(GPS),方向公差带小于该要素的位置公差带,故耦合公差带的大小为Tp,方向与基准平面,位置在尺寸公差带内平动,可由图1的阴影区域表示。在SDT公差模型中,将实际平面用理想表面SS表示,平面几何要素误差由理想表面SS的α,β,w3个分量的变动描述。则由图1可知,理想表面SS移动误差分量w的变动区间为TD,由尺寸公差控制,转动误差α,β的变动区间为Tp,由平行度公差控制。

综上分析,在尺寸公差与平面度公差耦合作用下,平面几何要素的SDT分量变动不等式为

图1 多公差耦合作用下的平面公差带Fig.1 Plane tolerance band under multi-tolerance coupling

式中,TDU、-TDL分别为尺寸的上下偏差。

为使理想表面位于耦合公差带内,应对SDT公差模型中的分量添加约束关系为

利用2组数学不等式来表示耦合公差的数学模型,式1为误差分量的变动不等式,它表示了平面几何要素单个误差分量所允许的变动范围。式2为误差分量的约束不等式,它表示了平面几何要素各分量参数之间的变动约束关系,确保了误差分量取值的合理性。

通过上述分析可知,几何要素在SDT模型中移动误差分量由固定公差Ts决定,转动误差分量由平动公差Tt决定,其误差变动不等式可表示为:

约束方程可表示为

式中:T Smax、T Smin分别为固定公差的上极限和下极限;T tmax、T tmin分别为平动公差的上极限和下极限。

1.3 几何要素误差分量实际分布规律求解

在SDT模型中,约束不等式限制了几何要素的各误差分量在变动不等式所确定的变动区间内的运动,为了得到各分量的实际分布规律,文中依据误差分量值的随机性特点,以及约束方程的不合格率p,推导出约束不等式限制情况下的几何要素的各个误差分量参数的实际的分布规律,此方法相较于传统蒙特卡洛模拟法更为简便地建立误差分量实际分布规律与公差之间的函数关系。

在实际加工过程中,由于人、机、料、法、环等各类因数的影响,使得几何要素的各误差分量呈现一定的分布规律[17],其实际分布情况难以确定。因此,文中主要研究当各个误差分量服从正态分布且相互独立的情况下的实际分布规律[18]。当各误差分量符合正态分布时,各分量的分布特征可用均值μ和方差σ2来描述,当耦合公差都为对称分布时,均值μ=0。由于形位均为对称分布,尺寸公差可以通过改变公称尺寸化为对称分布公差,为了方便计算,可将各公差化为对称分布公差,此时耦合公差带服从对称分布,均值μ=0,故仅通过方差σ2就可表达各误差分量的分布特征。

1.3.1 蒙特卡洛模拟法求解几何要素误差分量实际分布规律

在传统的基于蒙特卡洛模拟法求解误差分量的实际变动区间中,首先根据式(3)中误差分量φ的变动不等式对其进行抽样(φ{α,β,γ,u,v,w}),模拟实际公差表面的变动,再根据式(4)对满足约束不等式的样本加以保留,不满足约束不等式的则剔除,当产生足够多满足条件的随机数样本后,对样本进行分析,求解出对应误差分量的均值与方差。具体流程如图2所示。

图2 各误差分量模拟抽样流程Fig.2 Simulated sampling process for each error component

1.3.2 以约束方程的不合格率求解几何要素误差分量实际分布规律

为了体现误差分量间的约束关系,文中将利用约束方程的不合格率p,推导各个误差分量的实际分布规律。

由于几何要素的各个误差分量服从正态分布,各分量可表示为

几何要素的各个误差分量标准差之间关系与分量变动区间有关,可表示为

式中:T i表示误差分量i变动区间的大小;σi表示几何要素误差分量i的标准差。

由于几何要素各个误差分量相互独立,约束函数由各分量线性组成,可知约束函数f也服从正态分布,可表示为

式中,σ2表示约束函数的方差。

当约束函数f的取值在[Tmin,Tmax]范围内的不合格率为p时,可知:

2 装配精度可靠度计算

雅可比矩阵模型是一种由机器人运动学理论发展而来的装配体误差传递模型[19],可用于表达零件功能元素由于制造或装配误差引起的微小变动,对装配功能要求的作用关系。文中基于该方法提出雅可比方差矩阵,用于表达各误差分量的方差对装配要求的影响关系,可表示为

式中:R为功能要求误差分量的方差,E i表示为特征i误差分量的方差,由于JEi为的雅可比矩阵,现定义JEi为的雅可比方差矩阵,用于表达特征i各误差分量的方差对R的影响关系,n为对R有影响的特征的个数。

基于雅可比旋量方差模型对实际误差传递路径上的各误差分量进行累积计算,最终可获得装配体各误差分量的分布情况。笔者提出通过装配精度可靠度来评价的装配体精度指标,以可靠度作为评价装配精度性能的依据,即可用概率来评价装配体满足精度要求的能力,更符合实际生产情况。假设精度指标要求允许的最大误差范围为Ω,则可通过计算装配精度指标的分布密度函数在Ω上的积分求解装配精度可靠度,用R(t)表示可靠度,具体的表达式为

式中,E(X)为装配精度指标的分布密度函数。

3 实例分析

以Peng[20]论文中的简易顶尖尾座装配体为例,详细阐述了零件几何误差建模及装配精度预测流程,并通过分析对比误差预测结果,论证了文中方法的可行性及合理性。图3为简易顶尖尾座,其关键组成零件有顶尖、阶梯型底座和L型底座组成。零件的关键几何要素精度公差取值范围如表2所示。假设不考虑由于定位操作等引起装配误差,为了保证易顶尖尾座装配精度,要求顶尖轴线在w方向的允许误差为±0.3 mm,可靠度为98%。其中,小结合面F3和F4装配误差仅对顶尖v移动方向误差分量有影响,故可忽略不计,文中假设几何要素的误差分量均服从正态分布,则具体计算流程如下。

图3 顶尖尾座装配简图Fig.3 Top tailstock assembly diagram

表2 顶尖尾座关键几何要素公差项Table 2 Top tailstock key geometry feature tolerances

3.1 几何要素误差分量的方差求解

1)以约束方程的不合格率求解几何要素误差分量方差以平面3.1为例,其的误差分量的方差计算方法具体如下:

由式(3)可得到误差分量的变动不等式:

由式(4)可得到误差分量的约束不等式:

现假设约束方程的不合格率p=1.24%,根据式(5)～式(9)可求出各误差分量实际变动区间。

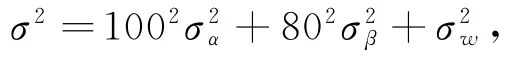
联立以上3个方程可得:

3.2 蒙特卡洛模拟法求解几何要素误差分量方差

在传统的基于蒙特卡洛模拟法求解误差分量的实际变动区间中,首先根据式(3)中误差分量φ的变动不等式对其进行抽样(φ={α,β,γ,u,v,w}),模拟实际公差表面的变动,再根据式(4)对满足约束不等式的样本加以保留,不满足约束不等式的则剔除,当产生足够多满足条件的随机数样本后,对样本进行分析,求解出对应误差分量的方差,以平面3.1为例,具体流程图2所示。

图2中,K为合格样本数量,N1、N2为常量,目的是为了防止前面的误差分量抽样值过大,导致后面的误差分量无法取到满足约束不等式的值而使抽样过程陷入死循环。

对保留的样本进行分析,求解出对应误差分量的方差。

通过对比2种求解误差分量方差的方法发现,求解结果近似相同,且以约束方程的不合格率求解几何要素误差分量方差相较于蒙特卡洛模拟法更为简便,故验证了以约束方程的不合格率求解几何要素误差分量方差合理性及可行性。同理可以约束方程的不合格率求解各几何要素误差分量的方差:

柱面轴线2.3误差分量的方差:

柱面2.1误差分量的方差:

柱面1.1误差分量的方差:

柱面1.2误差分量的方差:

3.3 基于雅可比旋量方差模型的装配体精度可靠度计算。

由式(10)可知,装配体的雅可比旋量方差模型为

经过计算:

则w方向误差分量标注差为σw=0.096 5。

在误差预测结果中,顶尖轴线在w方向废品率为5%时,对应的允许误差变动范围为[-0.328 74,0.328 74],经计算可知w方向的误差分量标准差为0.168,Peng的误差预测模型中未考虑误差分量之间的相互约束关系,使得各几何要素误差分量的变动范围大于实际值,进而令最终装配误差预测值偏大。文中装配误差预测值为0.096 5,略小于Peng的预测值,相对而言更为合理。

由式子(11)可知,装配体精度可靠度为

经过计算,顶尖尾座装配精度可靠度为99.81%,故装配体达到装配精度要求。

4 结 论

1)提出了一种在多公差耦合作用下的几何要素误差建模方法,利用约束方程的不合格率p,推导出了各个误差分量参数的实际的分布规律,建立了几何要素误差模型。

2)基于雅可比旋量模型,提出了雅可比方差矩阵,表达各误差分量的方差与装配体精度指标方差的之间影响关系,进而建立了装配误差建模,实现了装配精度的预测。

3)提出了以可靠度作为评价装配精度性能的依据,使得可用概率来评价装配体满足精度要求的能力,更符合实际生产情况,最后以顶尖尾座装配精度预测为例,验证了该方法的合理性及可行性。