燃料电池空气供应系统非线性鲁棒控制

马彦，朱添麟

(1.吉林大学通信工程学院，吉林 长春 130012；2.吉林大学汽车仿真与控制国家重点实验室，吉林 长春 130012)

随着人们对环境以及能源问题的日益关注，燃料电池广泛应用在汽车混合动力系统中。燃料电池种类很多，质子交换膜(Polymer Electrolyte Membrane,PEM)燃料电池因其高效率、低运行温度和零排放而被认为是未来电动汽车最有潜力的电源之一[1]。PEM燃料电池系统中，空气供应子系统消耗最多电能，其所需的寄生功率可占PEM燃料电池总输出功率的25%。因空气压缩机和空气供应管道动力学特性，在供应空气时有时间延迟。负载电流阶跃上升，较大时间延迟可能会导致电堆阴极中氧气短缺，电池输出电压下降和电池堆阴极被淹没，这会缩短PEM燃料电池使用寿命；空气供应量过高，空气压缩机会消耗过多功率，降低了系统的净输出功率[2]。电堆阴极压力也影响燃料电池系统电压[3]。阴极压力逐渐增大，水蒸发速率将会减小，质子交换膜含水量增加，质子传递速度加快，燃料电池内部电化学反应变剧烈，燃料电池电压升高。不断提高阴极压力，扩散层中的水含量逐渐上升，有效的孔隙率降低，燃料电池电压缓慢变化[4]。

在空气供应系统模型研究方面，Pukrushpan基于PEM燃料电池系统机理建立了系统级的九阶非线性系统模型，将电堆阴阳两极的流体动态特性加进模型中。由于该模型有九个状态变量，基于模型的控制器的实现会更加复杂[5]。在此基础上，K. W. Suh通过合理的假设，建立了空气供应系统四阶模型，并利用文献[5]进行模型精度验证[6]。Talj通过用电堆阴极压力代替空气供应系统四阶模型中的氧气和氮气的分压，建立了简化的空气供应系统三阶模型[7]。Zhao dongdong将文献[5]中回流管道固定开度的背压阀替换成可调开度的背压阀，控制背压阀的开度来调节电堆阴极压力，建立了面向过氧比与电堆阴极压力控制的六阶多输入多输出模型[8]。

在空气供应系统控制方法研究方面，W. Ki Na利用简化的燃料电池电堆模型，设计了反馈线性化的非线性控制器来调节电堆阴阳两极压力，但是忽略了空气供应系统模型及系统存在的参数不确定性，这会对系统性能有很大影响[9]。马彦在考虑了空气压缩机电压以及过氧比的约束条件下，应用模型预测控制对燃料电池空气供应系统进行控制与试验验证，在负载小范围变化时取得较好控制效果[10]。F. Zhang使用非线性三步控制方法对空气供给系统过氧比进行调节，同时添加辅助电源来避免过氧比下冲过大，通过试验证明该控制方法的有效性[11]。Zhao dongdong使用分数阶PID控制方法实现了对期望的过氧比与阴极压力的跟踪控制，结果表明系统参数变化影响控制效果[8]。

本研究针对PEM燃料电池空气供应系统的过氧比和阴极压力的控制进行了如下研究：1)建立PEM燃料电池空气供应系统多输入多输出模型；2)考虑模型在实际运行过程中存在的参数不确定性，设计了微分观测器观测不可直接测量的电堆阴极压力，同时设计了非线性鲁棒控制器实现期望过氧比和阴极压力的跟踪控制；3)仿真试验验证模型精度及控制策略的有效性。

1 PEM燃料电池空气供应系统建模

PEM燃料电池进气系统是由空气供应子系统和氢气供应子系统组成，系统结构见图1。空气供应子系统由空气压缩机、空气供应管道(含加湿冷却器)、电堆阴极、回流管道(背压阀)等装置组成[6]。以下对空气供应子系统各部分进行机理分析。

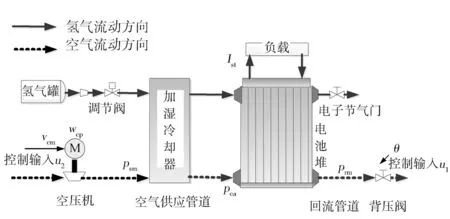
图1 PEM燃料电池进气系统结构

1.1 空气压缩机模型

空气压缩机是由转矩所控制的永磁同步电机驱动，用于向燃料电池系统的电堆阴极提供氧气。压缩机角速度wcp动态模型为

(1)

式中：Jcp为空气压缩机转动惯量；τcm和τcp分别为电机电磁力矩和空气压缩机负载转矩。τcm和τcp表达式如下：

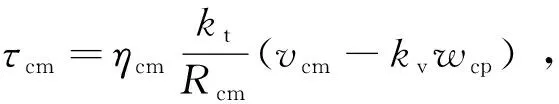
(2)

(3)

式中：kt，Rcm和kv为空气压缩机机械系数；ηcm为电机机械效率；vcm为空气压缩机输入电压；Cp为空气的比热容；γ为空气比热系数；ηcp为空气压缩机效率；psm为空气供应管道压力；Tatm和patm分别为空气压缩机入口空气温度以及压力；Wcp为离开空气压缩机的空气质量流量。

1.2 空气供应管道模型

空气供应管道为空气压缩机和冷却加湿器以及电堆阴极之间管道的集总部分。由理想气体定律、能量守恒定律以及空气热力学，可得空气供应管道压力psm表达式：

(4)

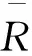
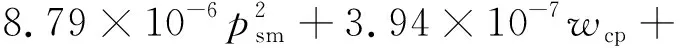
(5)

离开压缩机时空气温度Tcp为

(6)

1.3 电堆阴极气体模型

由质量与能量守恒原理，可得阴极内部氧气压力pO2和氮气压力pN2表达式：

(7)

(8)

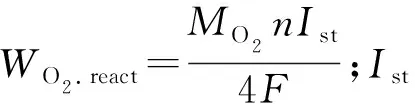
1.4 回流管道模型

回流管道是电堆阴极出口处与外界空气之间的管道，包含背压阀。回流管道模型可由质量守恒以及理想气体定律求出，表达式为

(9)

式中：Trm,Vrm和Wrm.out分别为回流管道的温度、体积和出口处质量流量。

Wrm.out可由非线性的喷嘴方程求出：

(10)

式中：CD,AT分别为回流管道中背压阀的阀门因数、阀门面积；θ为阀门开度，阀门开度范围在0～1。

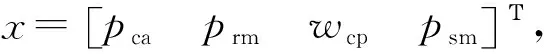
(11)

式中：u1为回流管道的背压阀阀门开度；u2为空气压缩机控制电压；d为可测的负载电流；状态量x1为电堆阴极压力pca；x2为回流管道压力prm；x3为空气压缩机转速wcp；x4为空气供应管道压力psm；ci(i=1,…16)是常数，如附录A所示。

PEM燃料电池系统过氧比λO2定义为[5]

(12)

式中：WO2,in和WO2,react分别为电堆阴极内部氧气进气量和电化学反应消耗氧气量；c17和c18是常数，如附录A所示。当λO2小于1时，燃料电池系统将会出现氧缺乏现象，当λO2较大时，空气压缩机消耗功率过高，本文参考文献[5]、文献[12]和文献[13]，选取过氧比期望值为2。

阴极压力影响燃料电池电压(见图2)。燃料电池系统在实际运行时电堆电流密度通常在0.5～1.3 A/cm2区间内，电堆阴极压力为200 000 Pa与阴极压力为250 000 Pa条件下，燃料电池单体输出电压接近。当阴极压力小于200 000 Pa时，燃料电池电压明显增加，当阴极压力大于200 000 Pa时，燃料电池电压提高明显变慢，同时极化损失会相对增加。在考虑系统性能和极化损失情况下，阴极压力期望值200 000 Pa时电池性能得到改善[4]。

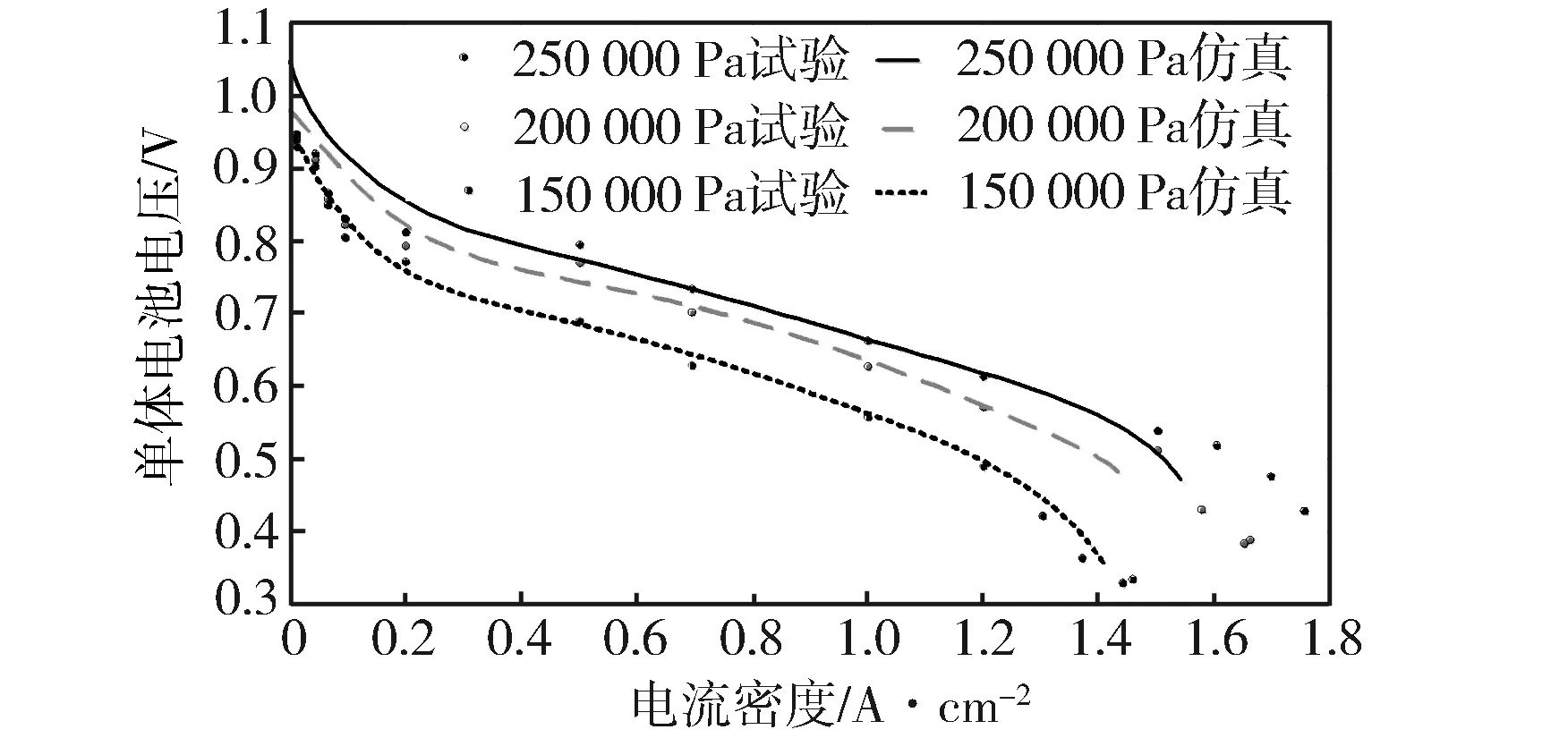
图2 不同阴极压力下，电流密度与单体电池电压曲线

2 非线性系统鲁棒控制器设计

为了跟踪系统期望的过氧比和电堆阴极压力，需要空气压缩机和回流管道背压阀协调控制。由于存在干扰负载电流d，对过氧比微分会使控制器设计更复杂。可定义虚拟输出

(13)

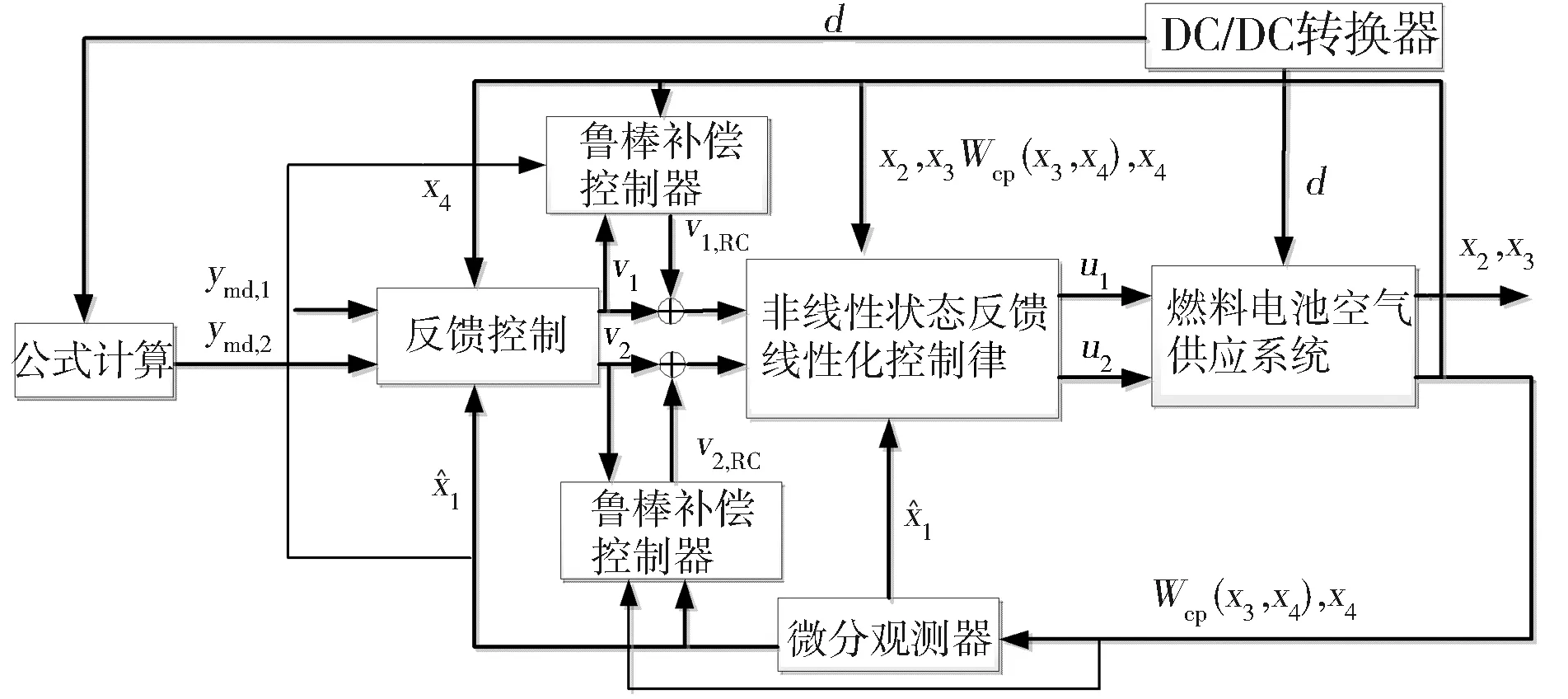
图3 系统结构

2.1 微分观测器设计

x4是可测量的状态变量，而在燃料电池堆内部湿气流环境下，使用传感器进行电堆阴极压力x1测量困难。为了能得到控制输出，需设计观测器估计电堆阴极压力x1。因此，可使用状态观测器替代物理传感器，得到不可测电堆阴极压力。通过调整式(11)中空气供应管道压力状态方程，得到电堆阴极压力x1的表达式：

(14)

电堆阴极压力可通过空气压缩机转速和空气供应管道压力，以及空气供应管道压力微分计算得到。空气供应管道压力可通过传感器得到，但其微分信号无法通过物理方法来获得。用数学微分器通过已知状态来获取其微分信号是有必要的[14]。蒲明提出采用Terminal吸引子函数代替符号函数的微分观测器，具有快速收敛的特性和强大的鲁棒性[15]。文中构造的观测器结构如下所示：

(15)

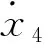
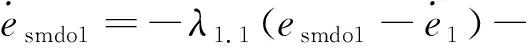
(16)

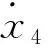
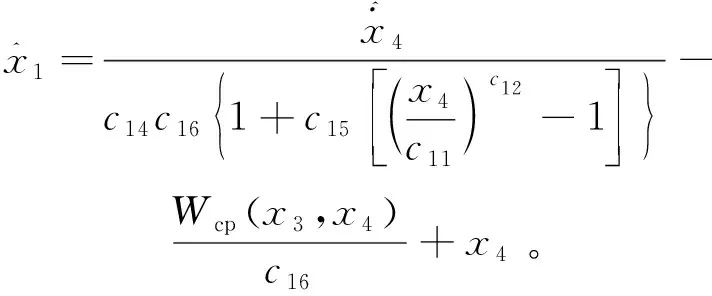
(17)

2.2 非线性鲁棒控制器设计

通过对系统进行反馈线性化，使电堆阴极压力通道和空气供应管道与电堆阴极之间压力差通道解耦成线性模型，对两个通道的线性标称模型分别进行标称控制器的设计，使标称线性的闭环控制系统具有期望输出特性。文中标称控制设计为状态反馈控制。考虑到基于反馈线性化的标称控制器不能去处理参数不确定性和外界的扰动等对闭环系统影响，所以在已进行标称控制器设计后的闭环系统基础上设计了鲁棒补偿器。最后，将状态反馈控制器与鲁棒补偿器结合构成了非线性系统鲁棒控制器。

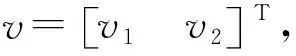
(18)

(19)

(20)

2.2.1反馈线性化控制设计

反馈线性化控制是对线性标称模型进行的控制器设计，是对被控系统进行的状态反馈控制。

(21)

由此得出状态反馈矩阵ki.FB，这里i=1,2，进而得到以下控制律：

(22)

对于被控系统，确定出状态反馈矩阵ki.FB，使得闭环系统为

(23)

进行傅里叶变换后为

(s2+k1.FB.2s+k1.FB.1)E1(s)=0，

(24)

(s2+k2.FB.2s+k2.FB.1)E2(s)=0。

(25)

合理调节参数ki.FB(i=1,2)，满足k1.FB.22≫4k1.FB.1，k2.FB.22≫4k2.FB.1，使式(24)和式(25)中所有根的实部是负数，或者实部是负数的复数，保证了标称闭环系统稳定性[16]。

2.2.2鲁棒补偿器设计

在对非线性系统控制器进行设计的过程中，不仅仅需要考虑模型非线性以及多变量耦合等因素带来的影响，还需要考虑系统中多种不确定性所带来的影响。系统的不确定性包含参数结构不确定性以及无法得知的未建模动态，本研究把这些不确定性都统一称之为等价扰动。存在的等价扰动会使所建立数学模型与真实的控制对象之间有差异，这会影响系统非线性控制。所以为了能够保证设计的非线性闭环系统性能稳定，需设计鲁棒补偿器来减小等价扰动带来的影响[17]。文中未给出不确定项的表达式，这里将这些不确定性的项归总为等价扰动，这些不确定性范数有界，设计的鲁棒补偿器可减小等价扰动对闭环系统的影响。在进行反馈线性化控制后，闭环系统为

(26)

电堆阴极压力通道和空气供应管道与电堆阴极之间的压力差通道的传递函数Gi(s)(i=1,2)可表示为

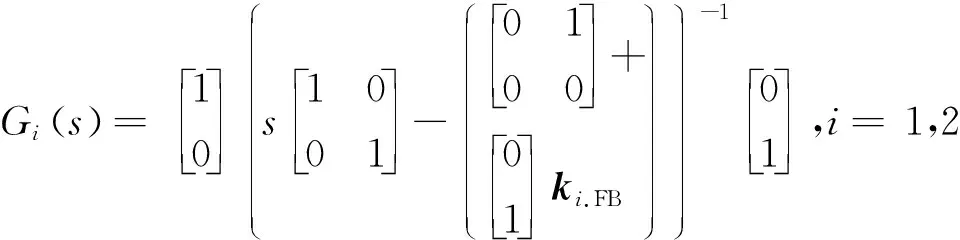
(27)

式中：s是拉普拉斯算子。结合等式(26)，得到以下系统输入输出关系：

(28)

设计的鲁棒补偿器为

(29)

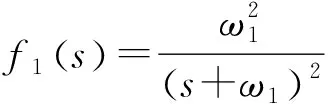
和ω2足够大，则滤波器增益接近1，可减小Δi(i=1,2)对闭环控制系统影响。但Δi(i=1,2)具体值却无法得到，在忽略Ei(0)(i=1,2)时，可得到：

(30)

进而可得到Δi(i=1,2)表达式：

(31)

最后，结合式(29)和式(31)，可得到不包括不确定项Δi(i=1,2)的鲁棒补偿输入：

vi.RC(s)=
-(1-fi(s))-1fi(s)Gi-1(s)Yi(s),i=1,2。

(32)

3 仿真及结果分析

3.1 模型精度与观测器效果验证

文献[5]中Pukrushpan九阶模型是经典的燃料电池系统级非线性模型，文献[7]、文献[13]和文献[18]用其针对改进的空气供应系统模型进行验证。为了验证本研究建立的模型以及微分观测器的效果，在MATLAB/Simulink中构建了空气供应系统模型。在负载电流、空气压缩机控制电压以及回流管道背压阀阀门开度都相同的条件下，与文献[5]中Pukrushpan模型进行可测输出的空气压缩机转速与空气供应管道压力比较，仿真参数见附录B。图4a示出给定的负载电流曲线，图4b和图4c分别示出空压机转速与空气供应管道压力响应曲线。由图4b和图4c仿真曲线可见，在仿真时间里Pukrushpan模型与本研究模型的输出曲线变化趋势相同，且最大的相对误差小于8%，而且存在的建模误差会在控制器设计过程中进行补偿，因此可基于本研究模型进行后续观测器和控制器的设计。

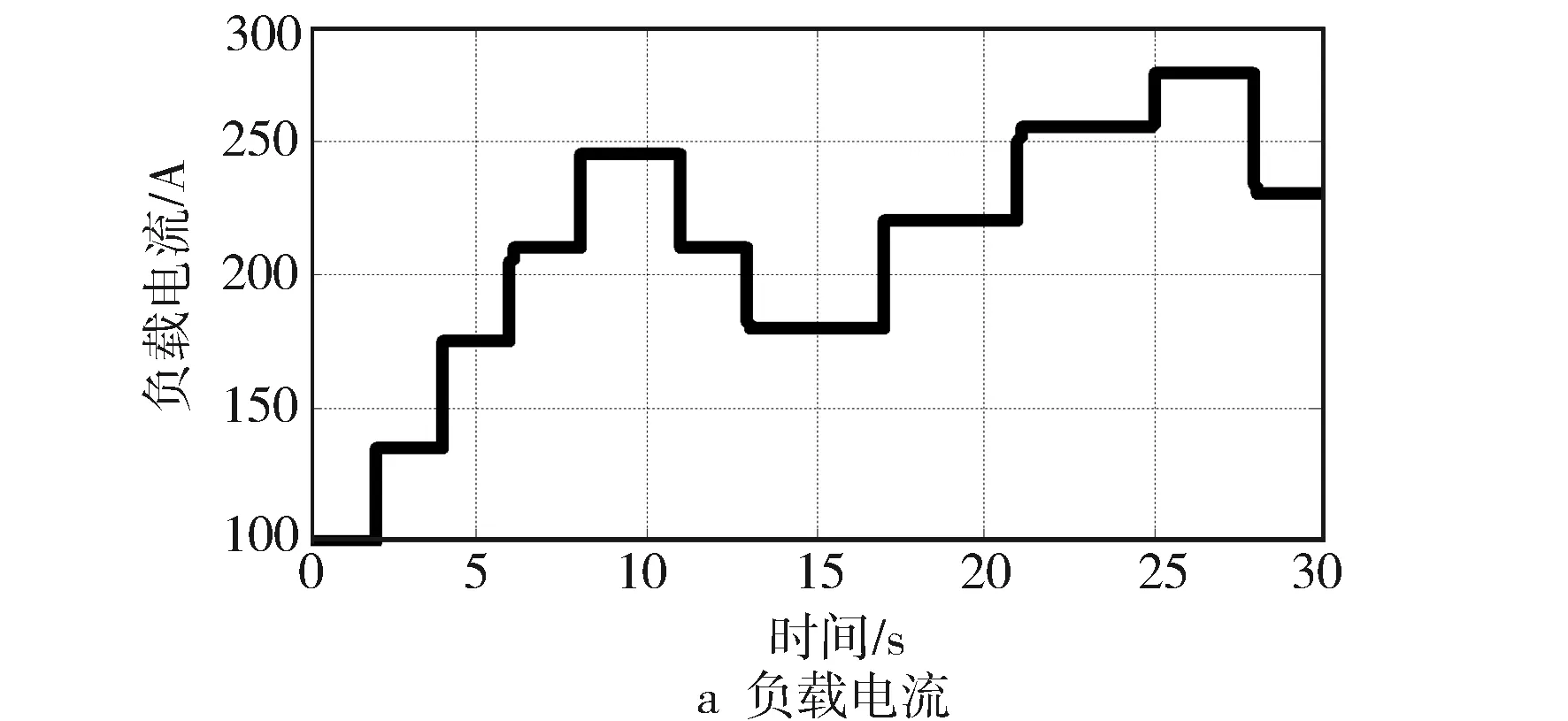
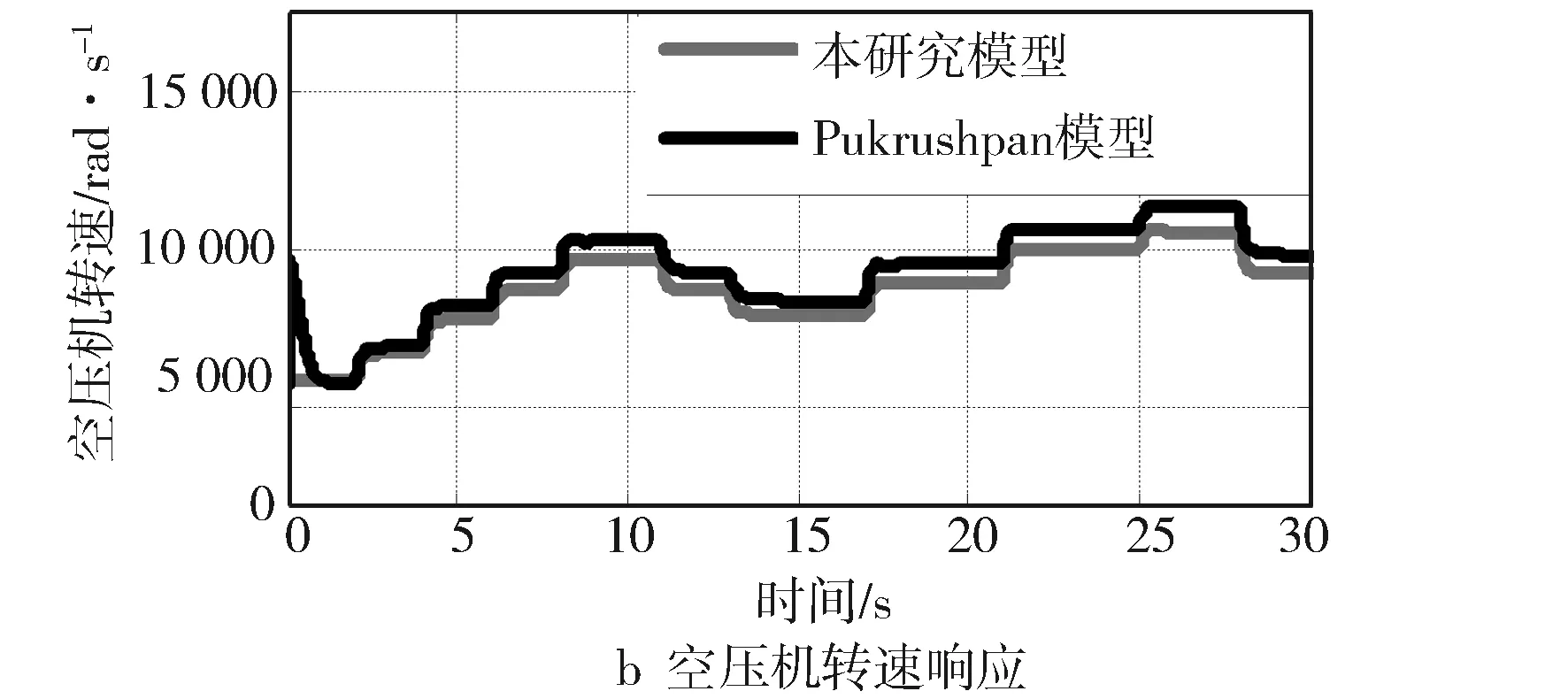
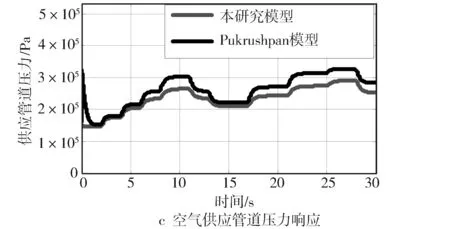
图4 Pukrushpan模型与本研究模型输出曲线对比

燃料电池空气供应系统中部分参数会在长时间运行过程中发生变化，参数调节为λ0.1=100，λ0.2=106，λ1.1=220，λ1.2=12.5，terminal吸引因子参数为l1=5，l2=7。图5示出系统参数在额定值附近变化(见表1)时的电堆阴极压力响应曲线和观测器误差曲线。观测值在实际值附近抖动，尤其是在负载电流阶跃变化时阴极压力观测误差变大，但电堆阴极压力的观测误差在±500 Pa范围内。观测精度低于0.3%且所设计的微分观测器抗干扰能力强，验证了所设计的微分观测器的鲁棒性和有效性。

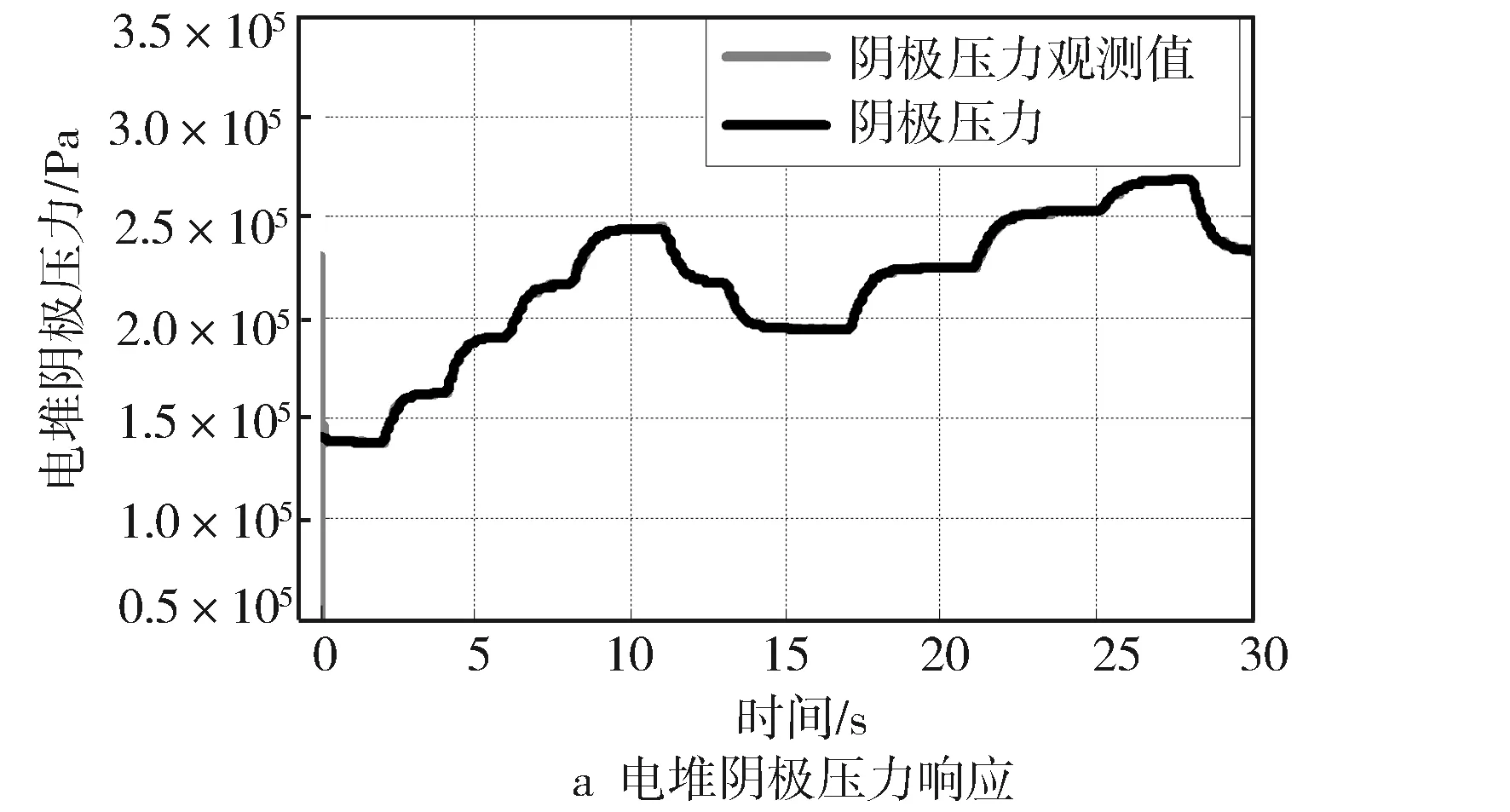
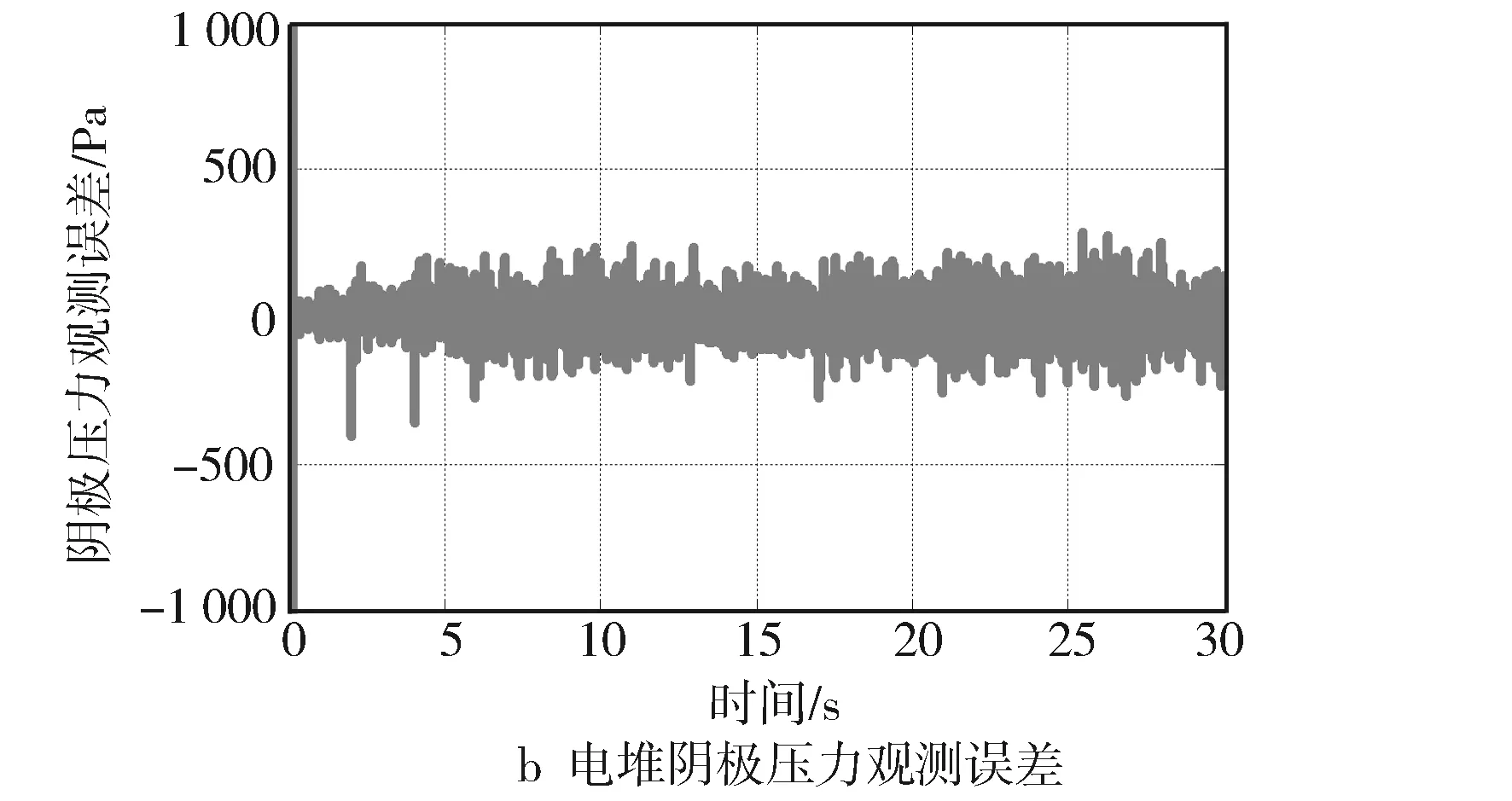
图5 电堆阴极压力观测和误差曲线

表1 PEM燃料电池系统参数变化

3.2 非线性鲁棒控制器效果验证

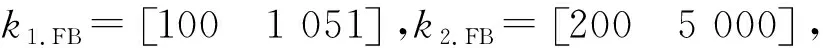
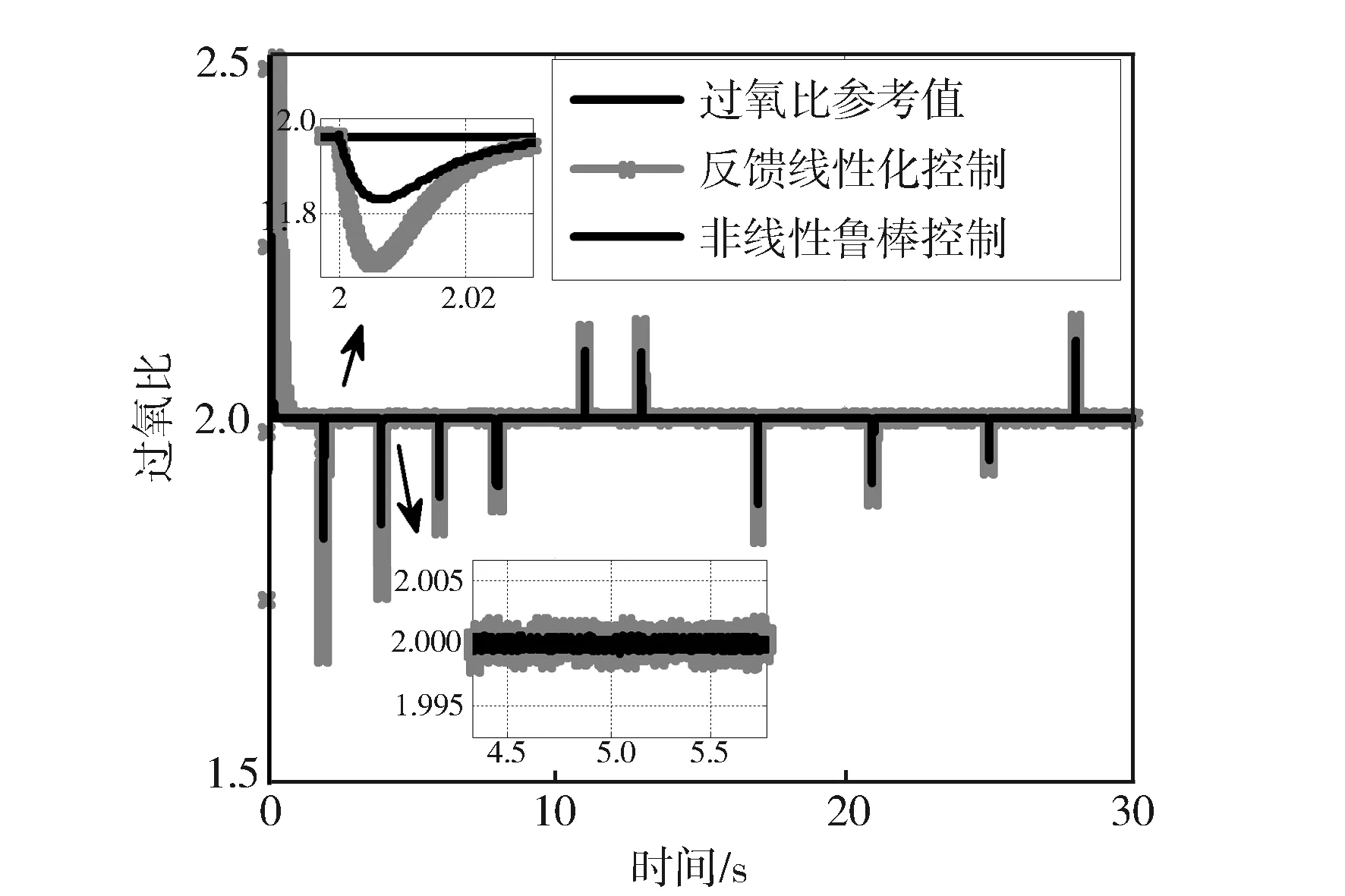
图6 不同控制器下过氧比响应曲线

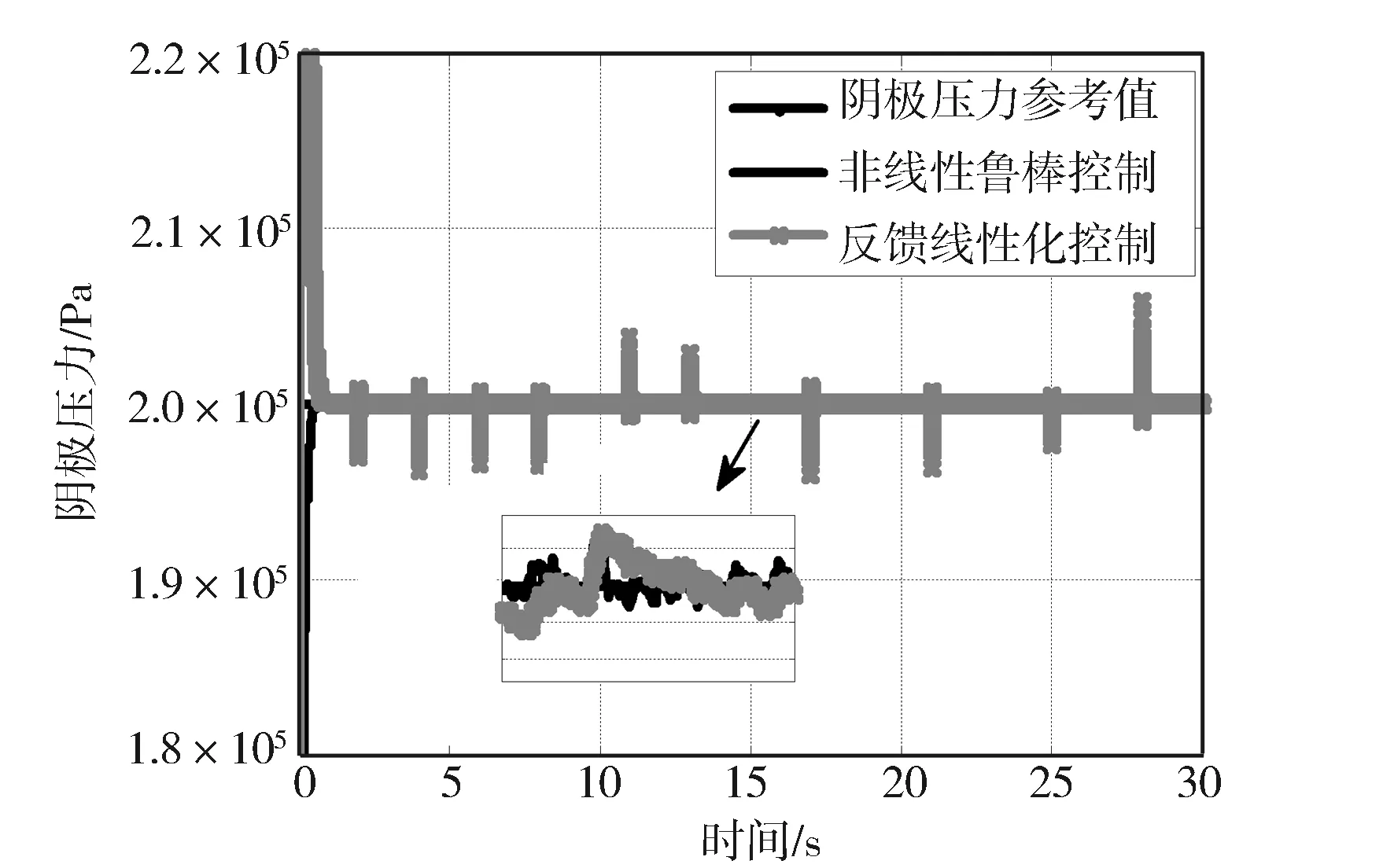
图7 不同控制器下阴极压力响应曲线

4 结束语

建立了面向过氧比与电堆阴极压力控制的PEM燃料电池空气供应系统多输入多输出模型，并进行了模型验证；在模型参数不确定时，采用微分观测器能够快速观测电堆阴极压力，最大观测误差小，表明微分观测器具有鲁棒性；对空气供应系统模型中电堆阴极压力与过氧比通道进行了解耦并分别设计了非线性鲁棒控制器,所设计的控制方法能够减小系统模型误差以及参数不确定性对PEM燃料电池空气供应系统控制的影响。该控制方法计算量小，在实际中可根据情况调节鲁棒补偿器参数，直至达到系统期望跟踪性能，表明了所设计的非线性鲁棒控制器的有效性和实际可操作性。

文中未给出系统不确定性的表达式，可对系统不确定性进一步研究；文中过氧比与电堆阴极压力期望值为定值，在后续研究中会根据实际负载电流进行期望值寻优；建立的模型是用Pukrushpan模型进行验证，后续研究应在PEM燃料电池试验台架进行验模和控制器效果验证。