增程式电动车自适应工况辨识策略研究
顾琰浩,吴晓东,许敏
(上海交通大学机械与动力工程学院,上海 200240)
当前,国家标准中汽车节能指标和测试工况日益严格,在发动机效率和动力电池容量难以突破的前提下,混合动力汽车成为短期满足节能指标的有效方案[1]。增程式电动汽车(EREV)在纯电动车基础上增加增程系统,可以有效提高续驶里程,并改善发动机工作条件和效率。
国内外学者已经对增程式电动车能量管理策略进行了研究。基于PMP算法的全局优化策略,凭借其计算速度快、计算量较动态规划(Dynamic Programming,DP)算法小的优点成为近年全局优化理论的研究热点[2-3]。S. Onori[4]使用打靶法得到协态变量的初值。Kim[5]研究表明,PMP算法结果与DP算法非常接近,因为可以合理地假设混合动力汽车的SOC变化很小,所以PMP全局优化控制策略的最优协态变量λ*被认为是一个常数。PMP全局优化控制策略以较小的计算量获得接近最优的优化效果,在离线优化中得到广泛应用。但是,PMP全局优化控制策略需要预知全局工况数据,无法用于车辆在线实时计算。
为了能够将PMP策略用于实时在线计算,提出自适应PMP控制策略,该策略通过实时提取车辆行驶数据,计算特征参数辨识当前工况,根据工况辨识结果调整自适应PMP控制策略的协态变量λ(t)。如何选择合适的工况特征参数进行工况辨识,对自适应PMP控制策略的优化结果具有重要影响,逐渐被研究者所重视。Kuhler[6]提出10个特征参数用于辨识工况,包括平均速度、平均加速度等。Song[7]根据经验选择特征参数。Montazeri-Gh等[8]利用相关性分析方法来挑选与油耗水平相关的特征参数。谢海明[9]选择最优百公里燃油消耗量v*作为相关性参数,通过分析特征参数与工况百公里燃油消耗量v*之间的相关性,选择合适的特征参数。将与工况最优百公里燃油消耗量v*相关性最高的特征参数作为工况辨识特征参数的自适应PMP控制策略(自适应PMP(v)策略)被广泛应用。
对于两种完全不同的工况,如果在PMP全局控制策略下具有不同的最优协态变量λ*和相同的最优百公里燃油消耗量v*,自适应PMP(v)策略会将两种工况视为等效,采用同样的协态变量进行控制,显然得不到理想效果。
针对自适应PMP(v)策略存在的问题,本研究提出将与工况在PMP全局优化控制策略下的最优协态变量λ*相关性最高的特征参数作为工况辨识特征参数的自适应PMP控制策略(自适应PMP(λ)策略),提高工况辨识结果与PMP控制策略匹配性。以现有的增程式电动车工况辨识策略为基础,通过建立多微行程的优化数据库,在传统聚类方法基础上提高辨识精度。基于车辆实时运行的坐标向量,对PMP优化算法的协变量进行在线自适应调整,实现对不同驾驶工况的动态优化,提高增程式电动汽车在未知工况下的燃油经济性。
1 车辆参数与建模
增程式电动汽车的基本结构与能量流动方向[10]见图1。增程式电动汽车在结构上属于串联式混合动力汽车,只由驱动电机通过传动装置驱动车轮,发动机和ISG电机组成的APU不直接和驱动轮连接,只作发电使用。
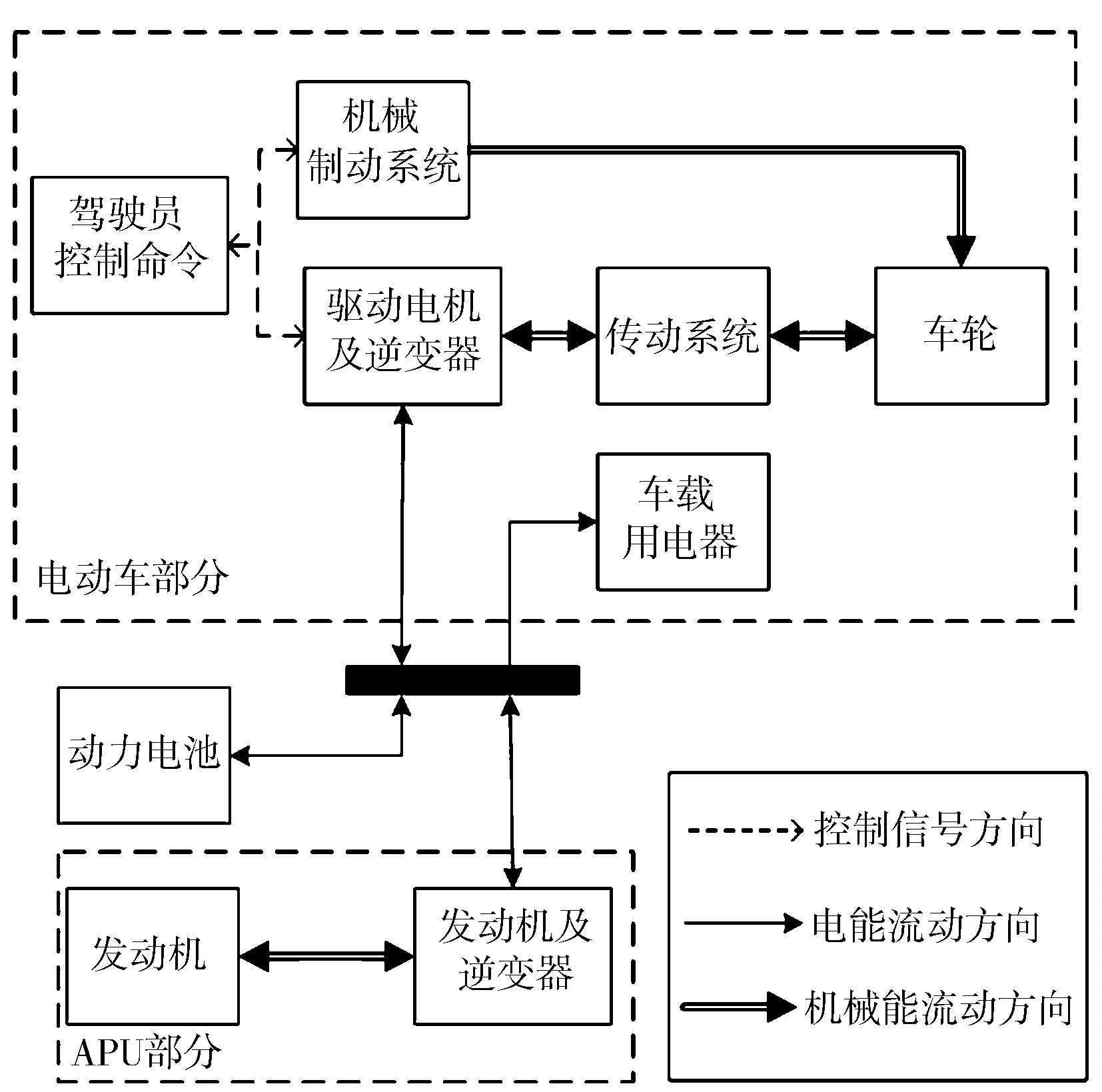
图1 增程式电动汽车基本结构和能量流
1.1 整车动力学模型
为了评价EREV的能量管理策略,建立了基于Matlab/Simulink平台的前向非线性车辆模型(见图2)。该模型拥有驾驶员模块,同时驱动电机具有制动能量回收功能,其他模块包括传动系统、制动器、动力学模型、APU模型、储能电池模型。
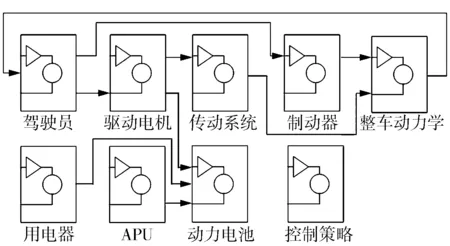
图2 Simulink平台下前向非线性车辆模型
式(1)为车辆行驶方程,驱动电机输出力矩需要克服道路荷载,这些荷载包括滚动阻力、空气动力阻力、坡道阻力和加速阻力。
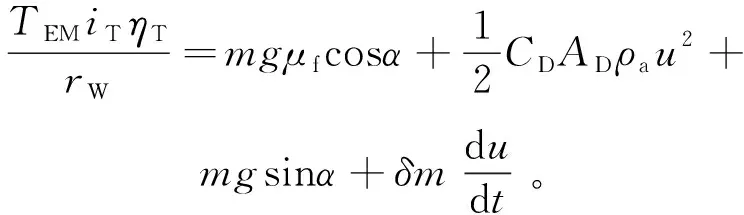
(1)
式中:TEM为驱动电机输出力矩;iT为传动系统减速比;ηT为传动系统效率;rW为车轮半径;m为车辆基准质量;g为重力加速度,9.8 m/s2;μf为滚动阻力系数;α为坡度角;CD为风阻系数;AD为迎风面积;ρa为空气密度,1.293 kg/m3;u为车速;δ为车辆当量惯量系数。
1.2 APU模型
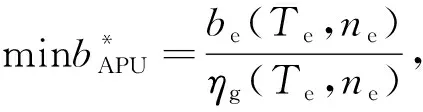
(2)

图3 APU燃油消耗率图及最高效率曲线
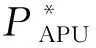
1.3 储能电池模型
增程式电动车的能量存储电池使用Rint模型进行设计[11](见图4)。这里忽略了温度和健康程度(SOH)对电池参数的影响。储能电池电流和荷电状态见式(3)和式(4)。
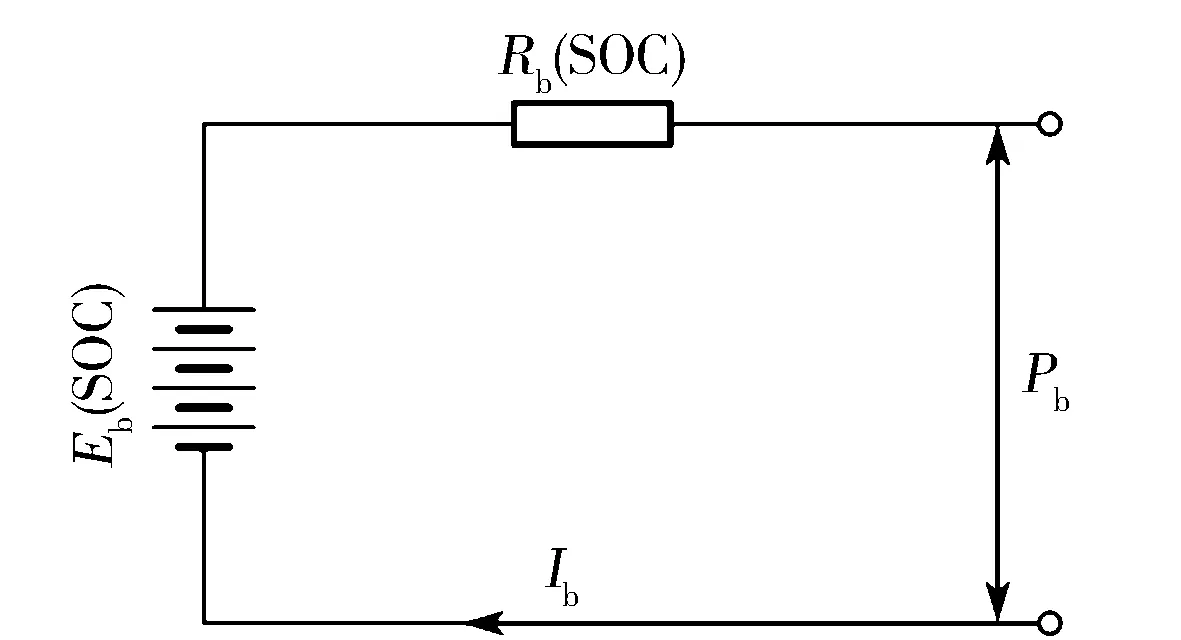
图4 电池Rint模型
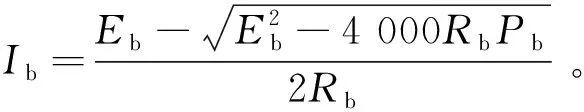
(3)
式中:Ib为动力电池输出电流;Eb为动力电池电动势;Rb为动力电池内阻;Pb为动力电池输出功率。
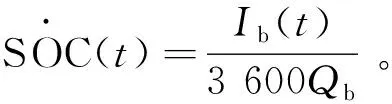
(4)
式中:SOC为动力电池荷电状态(State of Charge);Qb为动力电池电容量。
2 微行程样本与PMP控制策略
自适应控制中的样本需要有典型性、差异性和全面性。典型性是指单个样本要能突出地反映一类行驶状况;差异性是指样本个体之间要有明显区分;全面性是指样本整体需要覆盖尽可能多的现实可能。在工况循环、微行程和时间窗口这三种样本建立方案中,选择微行程作为样本创建方式,因为微行程具有完整的起停过程,微行程之间具有明显的典型性、差异性[12]。
2.1 微行程样本的建立
NEDC是欧洲、中国、澳大利亚等国家和地区现行使用的工作循环,由市区运转循环和市郊运转循环组成。WLTP为联合国推行的轻型汽车测试程序,在全世界范围内收集真实的行驶工况数据,包含低速、中速、高速和超高速4种工况区间。US06是美国高速度、高加速度工作循环。选择NEDC、WLTP、US06这3种工作循环作为样本数据,可以覆盖车辆运行的常见速度区间和加速度区间。
NEDC、WLTP、US06工作循环总计有16种微行程(见图5至图7),设微行程为M1,…M16。
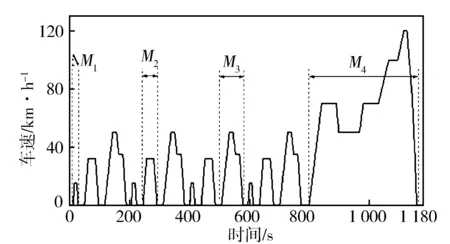
图5 NEDC工作循环和微行程

图6 WLTP工作循环和微行程
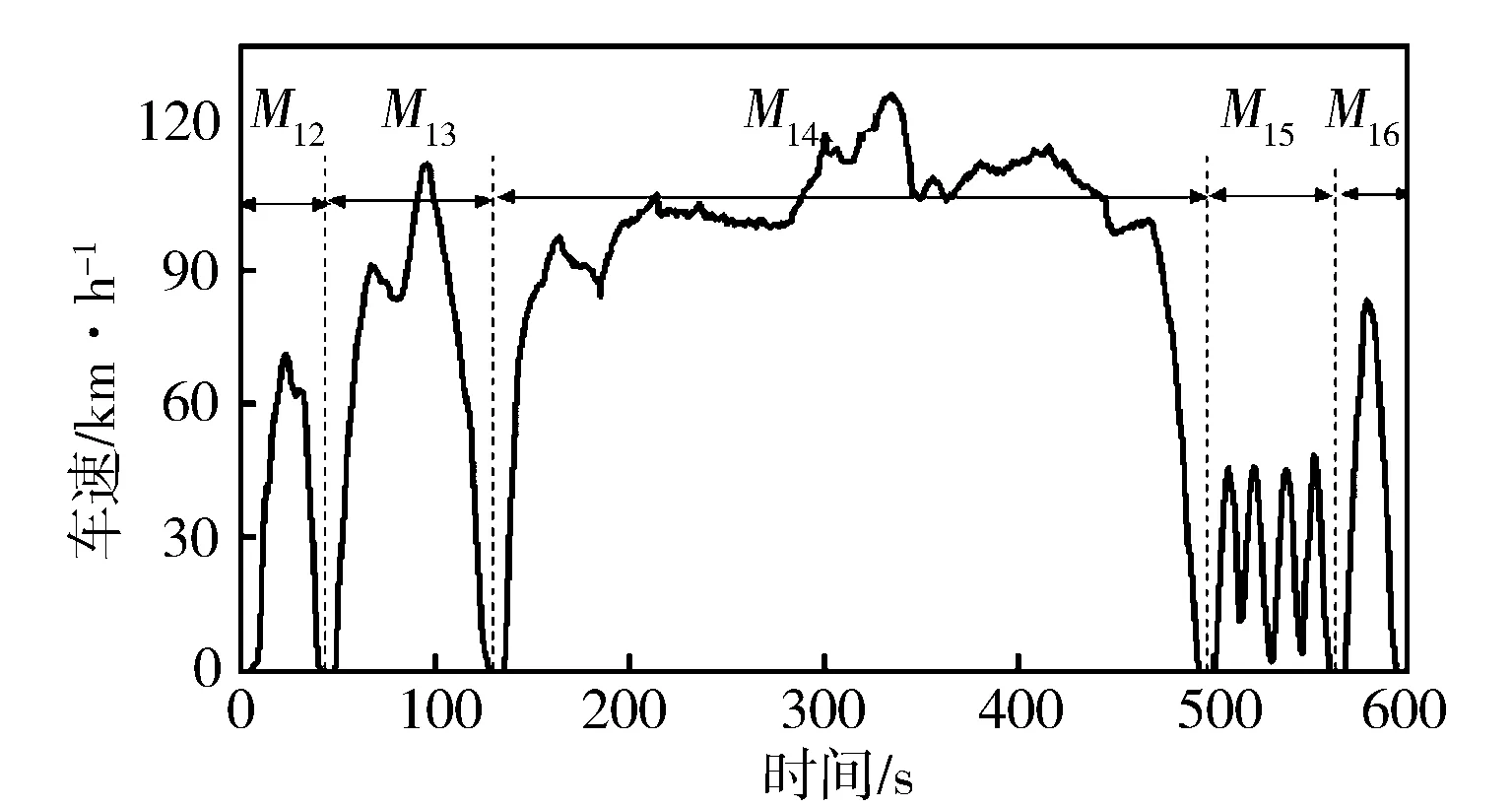
图7 US06工作循环和微行程
对于每种微行程Mi,通过以下方式获得对应的样本Yi:
1) 如果微行程Mi的时间长度不小于150 s,则微行程Mi直接作为样本Yi;
2) 如果微行程Mi的时间长度小于150 s,则重复微行程Mi,直到总时间长度不小于150 s,作为一个样本Yi。
通过以上方式,可以得到样本Y1,…Y16,样本时长Ti≥150 s。
2.2 PMP全局优化控制参数
苏联学者庞特里亚金在1957—1958年创立极小值原理。PMP控制策略目标参数:

(5)
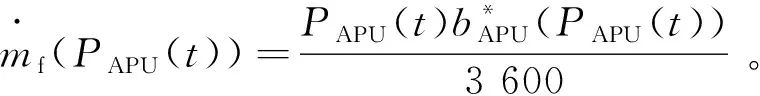
(6)
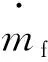
系统状态方程:
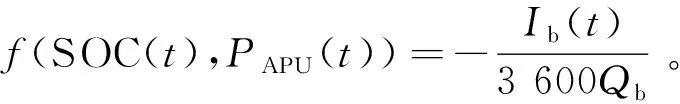
(7)
根据式(5)和式(7),建立哈密尔顿函数:
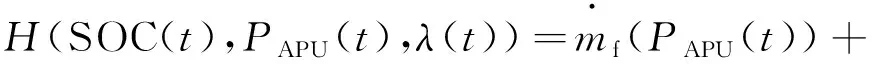
(8)
式中:λ(t)为协态变量。
当SOC在小范围内变化时,SOC(t)近似为常数[13]:
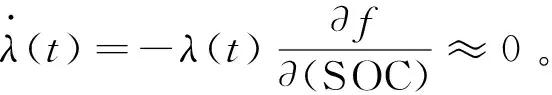
(9)
所以PMP全局优化控制策略所采用的最优协态变量λ*(t)可视为常数,且等于最优协态变量的初始值λ*(0),即有:
λ*(0)=λ*(t)=λ*。
(10)
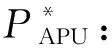
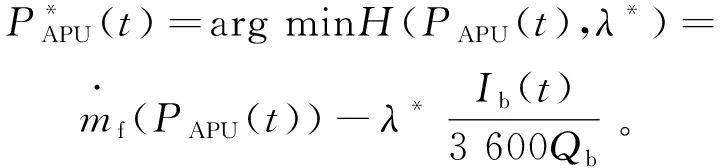
(11)
s.t. SOC(t0)=SOC0,
SOC(tf)=SOCf。
根据式(11),对16个样本分别使用PMP全局优化算法进行仿真,设定SOC0=0.3,SOCf=0.3,分别得到16个样本的最优协态变量λi*和最优百公里燃油消耗量vi。最优协变量组成向量λ*=[λ1*,λ2*,…λ16*]T,最优百公里燃油消耗量组成向量v*=[v1*,v2*,…v16*]T。
3 特征参数离线分析
为分析车辆行驶状态和样本的接近度,将样本和实际行驶的“车速-时间”关系转化为n维空间内的样本坐标向量φ和行驶坐标向量x。为保证自适应控制的精确性,降低车辆实时计算压力,样本坐标和行驶坐标应该在保留工况信息的同时具有较少的维度。
本研究选择最优协变量λ*作为相关性参数,通过相关性分析选择合适的工况特征参数进行工况辨识,并和以最优百公里燃油消耗量v*作为相关性参数的方案进行比较。
在后面的公式中,使用r代表相关性参数,两种方案中r分别是最优协变量λ*或最优百公里燃油消耗量v*。
3.1 样本特征参数提取
初步选择k个样本特征参数,本研究中k=21,特征参数列于表1,所有特征参数要求与样本时长无关。

表1 21个特征参数和意义
计算16个样本在t∈[0,Ti]区间内的k个特征参数值,得到样本参数矩阵A:

(12)
式中:aij为样本Yi的特征参数Cj的值,i=1,…16;j=1,…k。
对样本参数矩阵A进行零均值标准化:

(13)
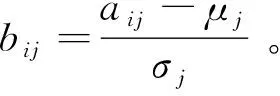
(14)
uj为特征参数Cj的样本平均值:
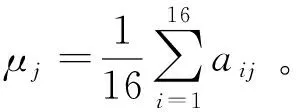
(15)
σj为特征参数Cj的样本标准差:
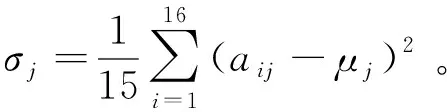
(16)
特征参数Cj的参数向量:
bj=[b1j,b2j,…b16j]T,j=1,…k。
3.2 特征参数相关性分析
特征参数Cj与相关性参数r的相关性,即参数向量bj与相关性参数向量r的相关性为

(17)
得到的特征参数Cj与相关性参数r相关性见图8。由图8可以看到,以最优协变量λ*和最优百公里燃油消耗量v*为相关性参数,分析特征参数的结果具有明显差异。对于特征参数C4,与最优协变量λ*体现正相关特性,与最优百公里燃油消耗量v*则体现负相关特性。对于特征参数C9,与最优协变量λ*体现正相关特性,与最优百公里燃油消耗量v*则相关度接近于0。
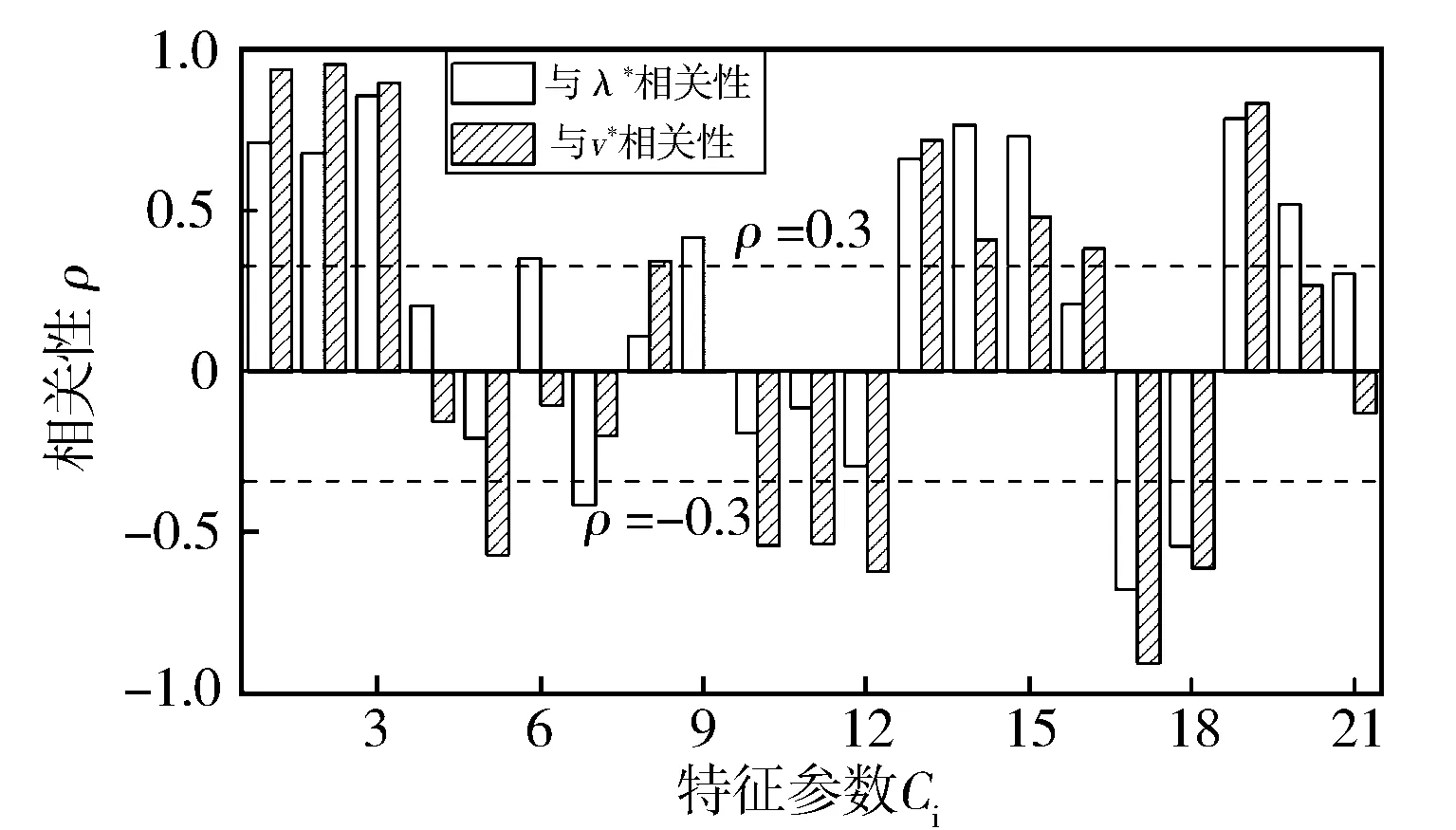
图8 特征参数与相关性参数的相关性
对特征参数Ci,Cj进行相关性分析:
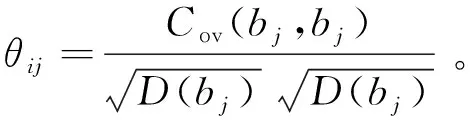
(18)
在选择的k个初步特征参数中,按照以下规则选择有效特征参数集Ω(r)。
1) 有效特征参数集Ω(r)中所有元素满足|ρj|>0.3,即Ω(r)所有特征参数Cj与相关性参数r的相关性大于0.3。
2) 有效特征参数集Ω(r)中任意两个元素满足|θij|<0.85,即当Ci和Cj相关性绝对值|θij|>0.85时,表示Ci和Cj在物理上有本质联系,只保留一种特征参数。
最终得到的有效特征参数集如下:
Ω(λ)={C3,C7,C9,C14,C15,C18,C20,C21},
Ω(v)={C2,C12,C13,C15,C16,C18}。
将Ω(r)中的特征参数重新编号,组成有效特征参数矩阵W(r):
W(r)=[w1, …wq]=[bl1, …blq]。
(19)
式中:q为有效特征参数矩阵W(r)中特征参数的数量。对于W(λ),q=8。对于W(v),q=6。wj=blj。
3.3 主成分分析
Ω(r)内特征参数之间仍然有一定的相关关系,说明这些特征参数反映的信息有一定的重叠。主成分分析是对原先提出的所有变量删去多余,建立尽可能少的新变量,使这些新变量两两不相关,而且这些新变量尽可能保持原有的信息。
对矩阵W(r)进行主成分分析,通常要求保留的主成分能够反映原来指标的85%以上。如图9、图10所示,对于W(λ)和W(v),前4个主成分方差贡献率占比分别为94.48%和98.58%,且相互独立。经过主成分分析,特征向量维度从8或者6降为4,使得车载VCU的计算量降低近50%,同时与工况信息参数r相关的信息得到保留。

图9 自适应PMP(λ)策略主成分与方差贡献率

图10 自适应PMP(v)策略主成分与方差贡献率
主成分变换公式为
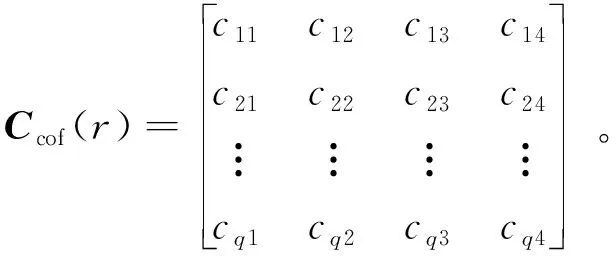
[F1F2F3F4]=W(r)Ccof(r)。
(20)
其中,Ccof(r)为变换矩阵:
(21)
3.4 坐标向量和坐标矩阵建立
对于样本Yi,样本时长为Ti,计算t时刻样本Yi的主成分,得到主成分坐标:
φi(t)=[φi,l1(t),φi,l2(t),…φi,lq(t)]Ccof,
(22)
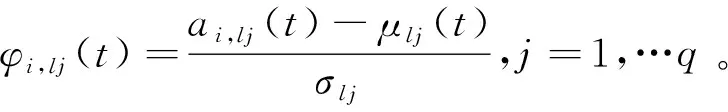
(23)
式中:ai,lj(t)为样本Yi在[0,t]区间内的“车速-时间”数据计算出的特征参数Clj的值。
将样本Yi每个时刻的样本坐标向量合并为样本坐标矩阵Φi,建立16个样本坐标矩阵:
Φi=[φi(1),…φi(Ti)],i=1,…16。
(24)
样本矩阵Φi的第t列向量代表t时刻样本Yi在空间中的坐标,从第1列到第Ti列代表样本Yi坐标从第1 s到第Tis的变化过程。
4 自适应PMP实时控制策略
4.1 在线样本识别
车辆实时运行过程中,每个微行程开始,t=0,自适应PMP控制系统开始执行,系统开始记录当前微行程内的车速信息,1 s记录一次,并转化为车辆实时行驶坐标数据库X。微行程结束时,车辆停车,自适应PMP控制系统关闭,车辆车速信息和实时行驶坐标数据库X清空。
在微行程内的t时刻,车速信息保存如下,最多保存150个车速信息。
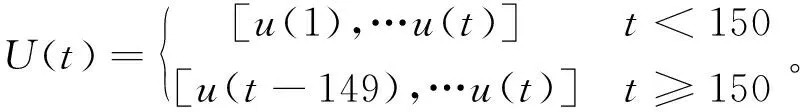
(25)
通过以下公式将U(t)中的车速信息转化为实时坐标向量:
x(t)=[xl1(t),…xlq(t)]·Ccof,
(26)
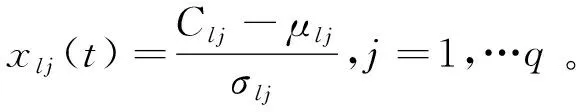
(27)
建立车辆运行过程中的行驶坐标矩阵X(t),X(t)每秒更新一次。
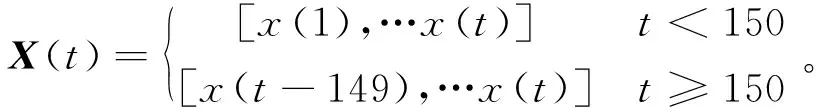
(28)
使用矩阵或者向量差的2-范数表征车辆实时行驶坐标与样本坐标的之间的距离。当t<150 s时,由于数据量少,使用全部坐标数据判别当前行驶工况与每个样本的接近度。当t≥150 s时,车辆实时工况趋向稳定,最后一个坐标向量包含了之前150 s内的所有数据,所以使用样本坐标矩阵和行驶坐标矩阵的最后一个坐标向量判断当前工况与每个样本的欧几里得距离。
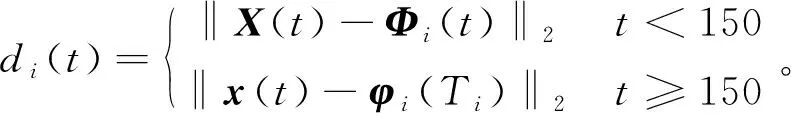
(29)
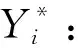
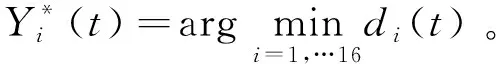
(30)
4.2 协态变量修正
对于式(9),固定SOCf=0.3,调整SOC0分别为0.29,0.295,0.3,0.305,0.31,得到PMP全局优化控制策略下SOC变化曲线与相应的最优协变量λ*。图11示出样本Y1的SOC变化曲线, SOC0=0.31时SOCf不为0.3,是因为当APU完全不启动时,依然无法达到SOCf=0.3。图12示出样本Y6的SOC变化曲线。
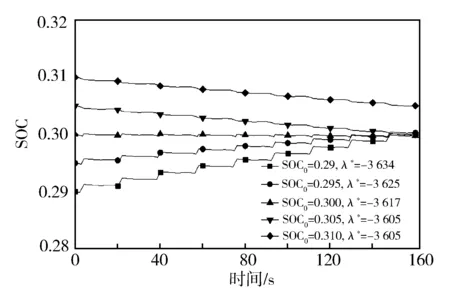
图11 样本Y1 SOC曲线与最优协变量
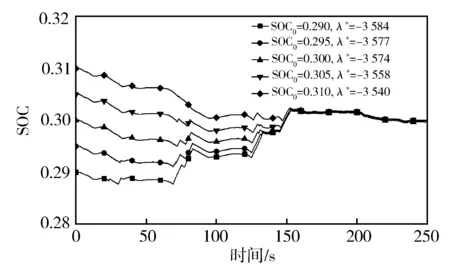
图12 样本Y6 SOC曲线与最优协变量
根据样本Yi和初始SOC0,考虑到当SOC(t)<0.287 5时电池电量过低,APU需要启动,而当SOC(t)>0.312 5时电池电量过高,APU需要关闭,修正后的自适应协态变量为
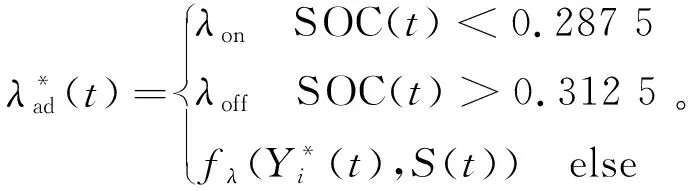
(31)
式中:λon是使APU必然启动的协态变量,本研究中λon=-3 700;λoff是使APU必然关闭的协态变量,本研究中λoff=-3 400;S(t)是实时SOC(t)进行离散化修正后的值,离散化方法见图13。
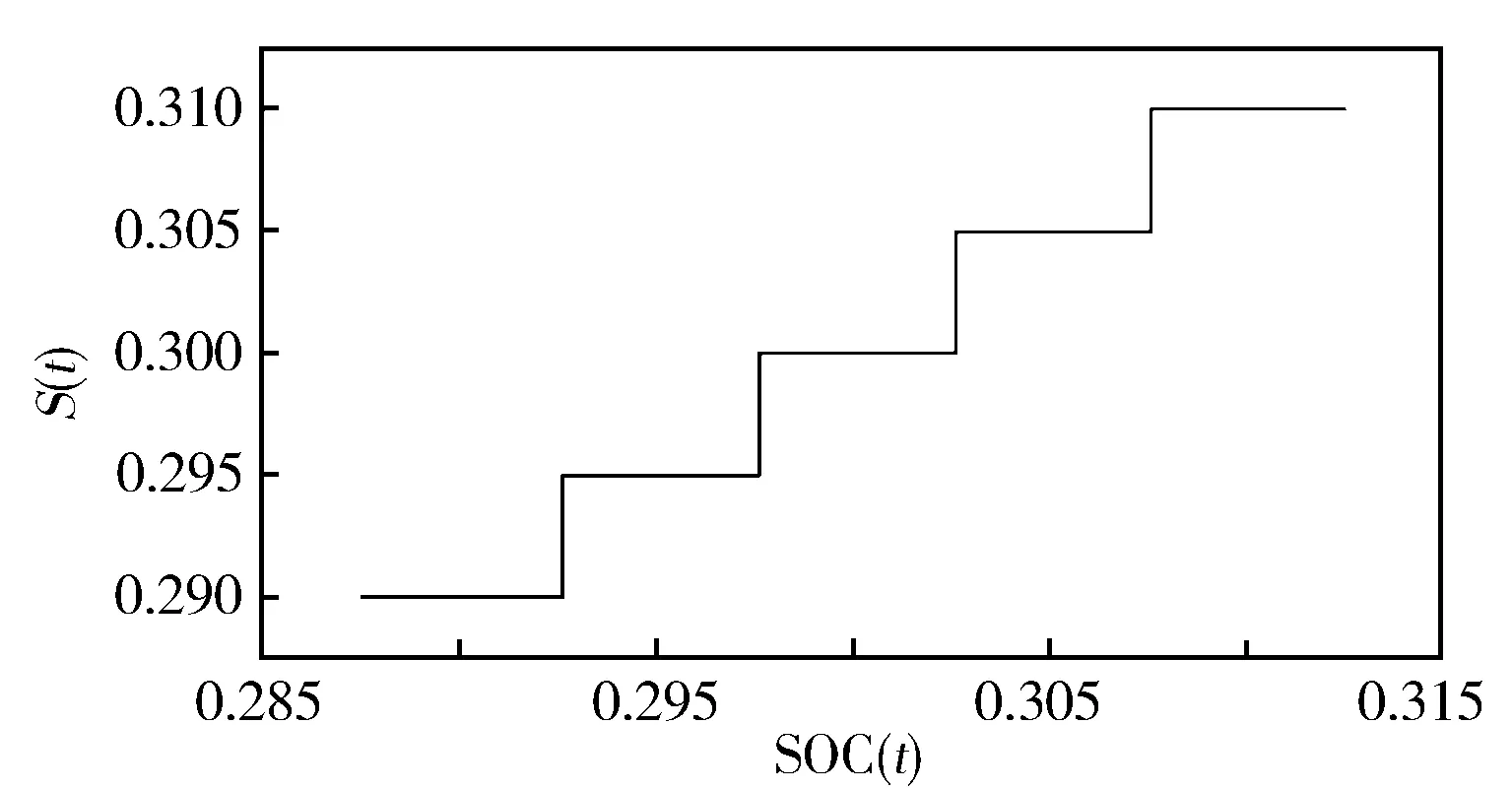
图13 SOC(t)网格离散化方式
4.3 试验仿真
分别使用SC03工况和HWFET工况进行PMP全局优化和自适应PMP控制策略的比较测试。图14示出SC03工况图,1个SC03循环过程中系统识别出的最接近样本见图15,在1个SC03循环中系统给出的最优协变量数值变化过程见图16。由图15和图16可以看出,在每一个微行程内,自适应PMP(λ)控制策略都比自适应PMP(v)控制策略更快进入辨识稳定状态。
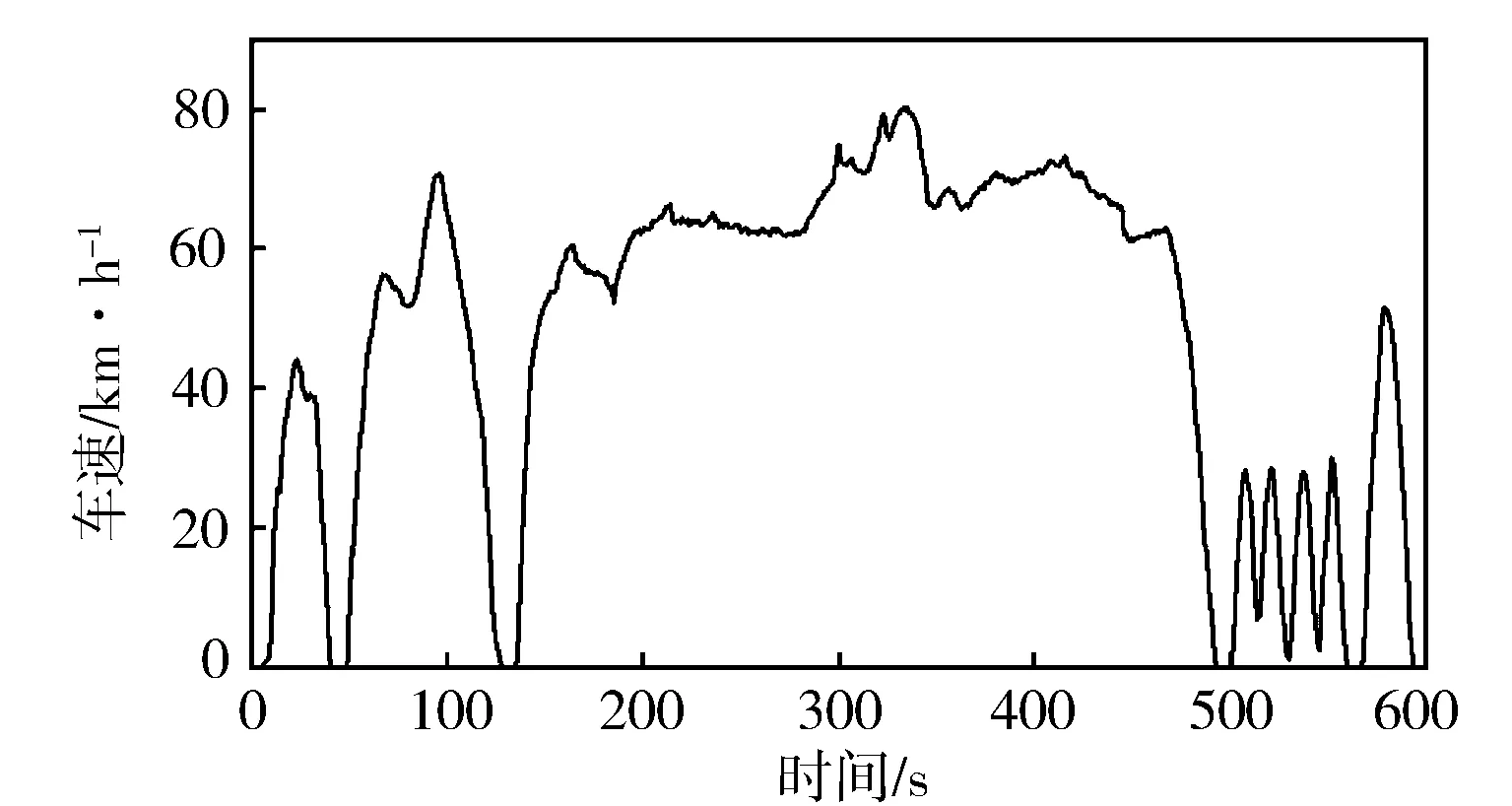
图14 SC03工作循环
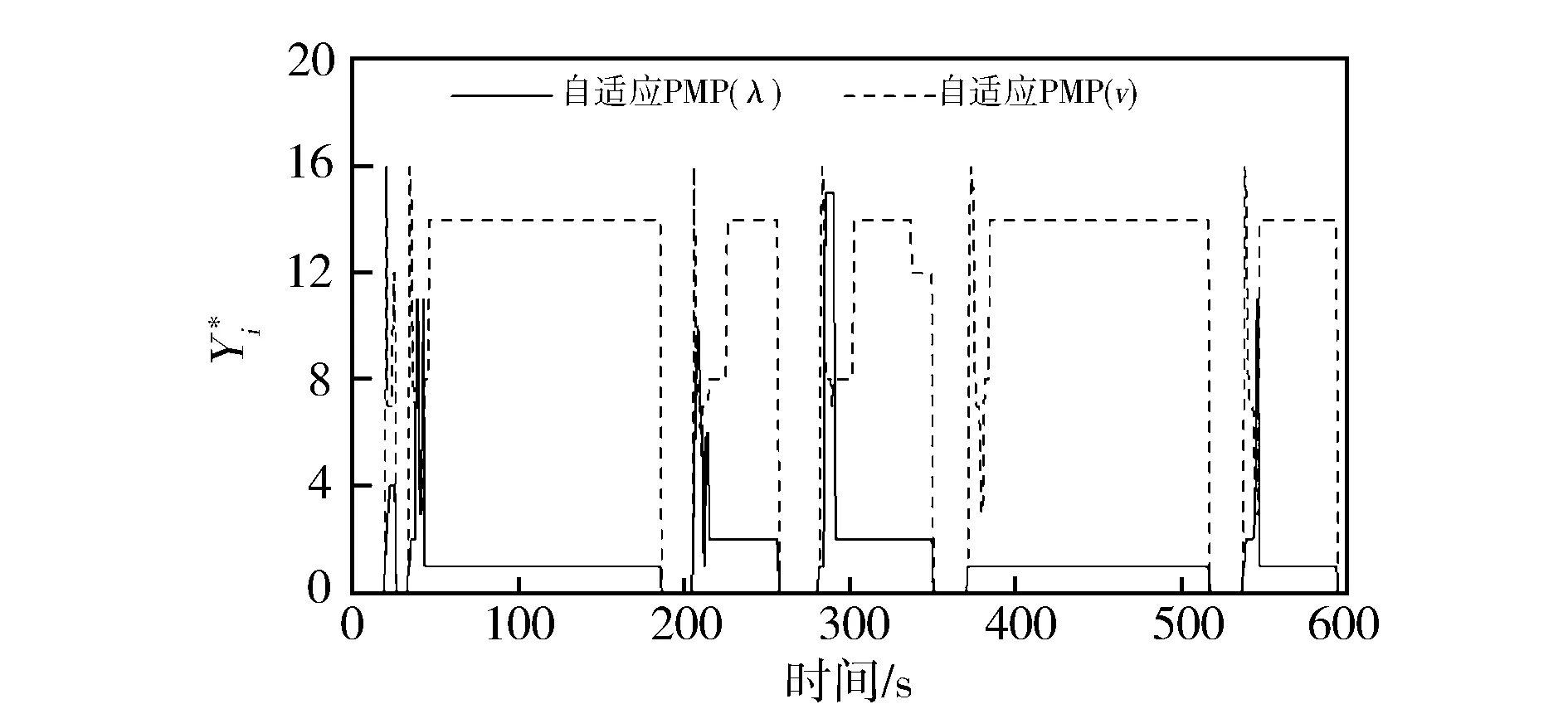
图15 自适应PMP策略对SC03工况的样本拟合
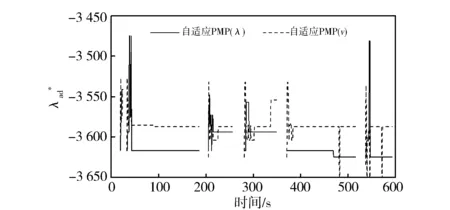
图16 自适应PMP策略在SC03工况下的协变量
图17和图18示出10个SC03工况和10个HWFET工况的仿真结果。油耗仿真结果显示,自适应PMP(λ)策略SOC边界为0.292~0.302(SC03)和0.3~0.306(HWFET),由于SOC在线修正算法,自适应PMP(λ)策略比全局优化PMP策略的SOC边界0.292~0.307(SC03)和0.275~0.31(HWFET)具有更小的SOC变化区间,有助于延长动力电池寿命。自适应PMP(λ)策略综合百公里燃油消耗量为3.700 L(SC03)和4.906 L(HWFET),比全局优化PMP策略高1.5%~1.6%。
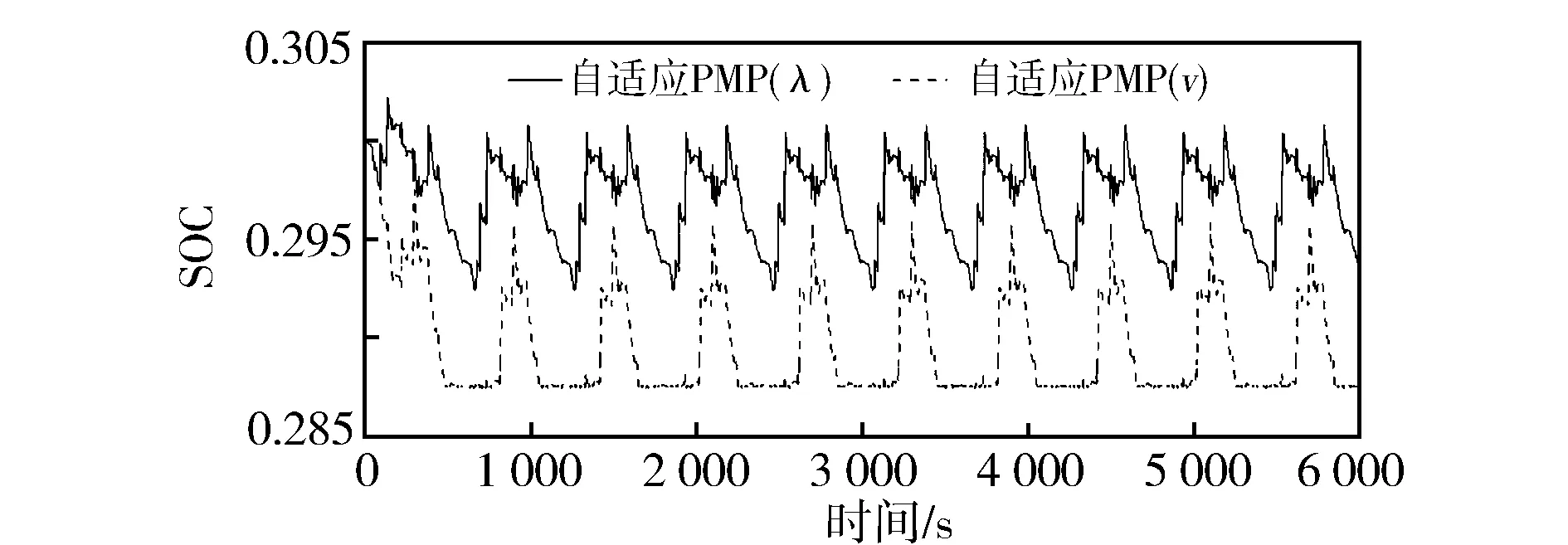
图17 SC03工况下PMP控制SOC变化曲线
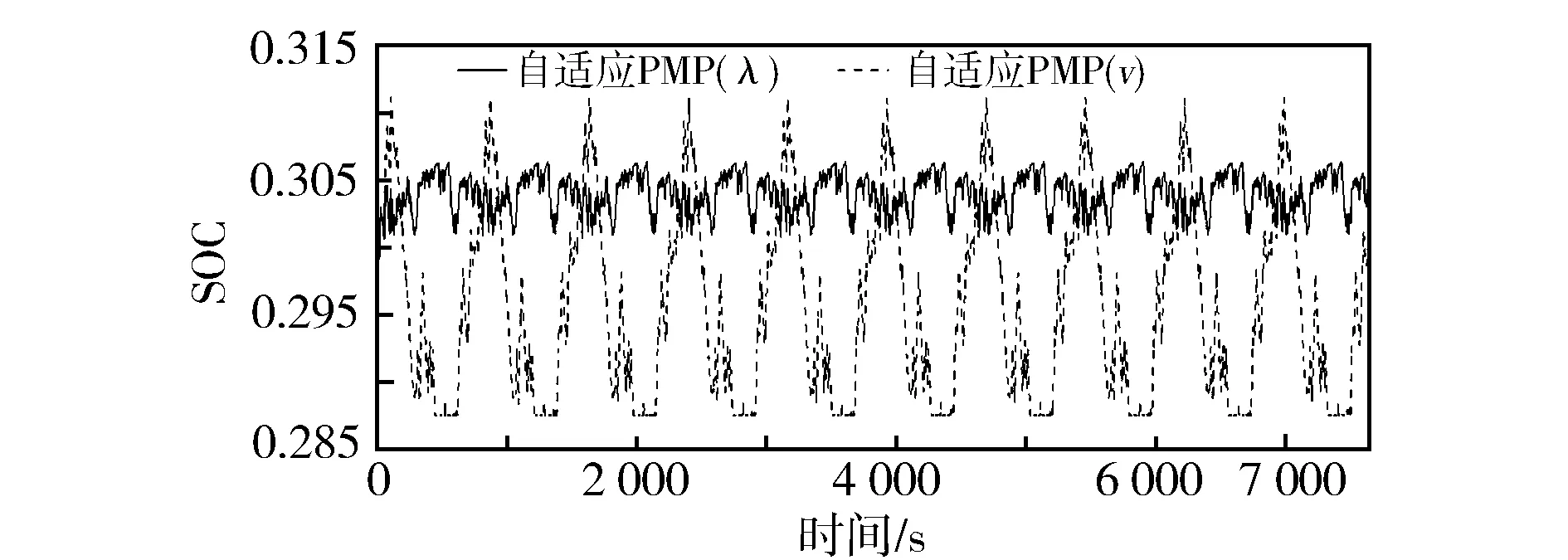
图18 HWFET工况下PMP控制SOC变化曲线
自适应PMP(v)算法SOC边界为0.287 5~0.3(SC03)和0.287 5~0.31(HWFET),实际上0.287 5是SOC在线修正策略所规定的硬边界,说明自适应PMP(v)算法无法实现SOC自适应回正。自适应PMP(v)算法综合百公里燃油消耗量为3.724 L(SC03)和4.937 L(HWFET),两种工况下均高于自适应PMP(λ)策略。
表2列出自适应PMP(λ)策略的实时优化结果。相比全局优化PMP算法提前知道工况数据下的结果,自适应PMP(λ)策略的油耗仅增加1.6%,但是无需提前知道工况数据,具有较高的工况自适应能力,有利于提高电池寿命。同时自适应PMP(λ)策略在电池寿命和油耗上都好于自适应PMP(v)策略。
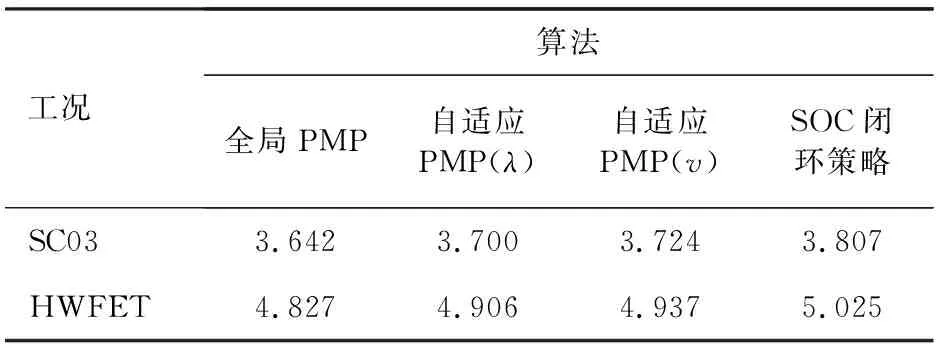
表2 百公里燃油消耗量仿真结果 L
5 结束语
以增程式电动汽车的能量优化管理为研究对象,分析了PMP控制最优协态变量与行驶工况特征参数的关系,实现增程式电动车在未知工况下PMP控制中的协态变量自适应优化。
以PMP控制策略协态变量作为特征参数相关性分析的依据建立工况识别策略,具有较好的工况识别效果,有助于节省燃油消耗,延长动力电池寿命。
在不同的控制策略下,根据控制策略的决策变量选择工况特征参数进行工况辨识,可以实现更好的自适应控制效果,优于根据经验选择特征参数和根据油耗选择特征参数进行工况辨识。

