专题式教学方法在机器学习基础教学中的应用探讨

杨荣根，陈维娜，杨 忠

（金陵科技学院 智能科学与控制工程学院，江苏 南京 211169）

0 引 言

教育分为基础教育和高等教育（专业教育），通过高考将基础教育中综合能力比较强、能够胜任更加复杂的专业学习的学生选拔出来，参加更高一阶的专业学习。无论从教育的类型说，还是从受众的对象来说，专业教学的性质都发生了改变，研究和探讨更加适合专业教学的方法非常必要。好的教学方法能够帮助学生建立系统观，将零散的知识串联起来，建立系统化知识体系，事半功倍[1-3]。

专业教学的成败事关人才培养质量的高低，所幸专业教学是可以把控的，因为专业教学也是由一门门专业课程元素构成的。针对每一门专业课程的特点，选择合理的教学方法，组织好每一门专业课程的教学，自然会提高专业教学的质量。一般而言，专业教学方法分为自顶向下、自底向上和专题式的教学方法。

人工智能专业是2018年4月设立的专业，旨在推动人工智能一级学科建设，培养我国人工智能产业的应用型人才[4-6]。机器学习是人工智能的一种方法和手段，目标是模拟或实现人类的学习行为，从纷繁复杂的数据中获取新的知识或技能，是一门新兴的交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等。机器学习基础是人工智能专业的一门专业基础课，对于这样一门新兴专业课程，涉及的内容如此之多，使得教学方法的选择显得尤其重要[7-10]。

1 专业教学一般方法

1.1 自顶向下教学法

自顶向下教学法是一种站在一定高度俯瞰式的教学，也可以看作是演绎式教学。这是应用最普遍的一种方法，例如高等数学中，先给出一般性的定理、结论，然后在这些定理成立的前提下推导出解题方法，最后在实际应用中将实际问题转化成适用这种定理使用的场景，解决实际问题[11-13]。

1.2 自底向上教学法

自底向上教学法是先给出一类具体问题的实现细节，一步步引导建立这类问题的概念模型，进一步抽象形成解决这类问题的理论模型。这种方法在专业教学中应用不是很广，但是在局部小范围可以尝试[14-15]。

需要指出的是，具有计算机科学与技术背景的人可能会联系到计算机网络教学中也有自顶向下和自底向上的教学方法，但那是针对计算机网络协议的层次模型的高低之分，协议的层次越高越接近应用，越低则越接近物理实现。所以网络的自顶向下和自底向上与这里的教学方法是有区别的。

1.3 专题式教学法

专题式教学法是在给定的专题基础上，讲述与这个专题有关的所有联系的知识，形成一个封闭的小系统。本文将重点讨论专题式教学法在机器学习基础教学过程中的应用。

2 专题式教学法在机器学习基础中的应用

机器学习基础的传统的教学过程是一种典型的自顶向下的教学方法，将与机器学习有关的所有数学理论作为一章，先行讲解，接下来介绍各种机器学习框架。对于具有一定基础的工程人员来讲这可能是一件很自然的事情，但是在本科生教学实践中，会有这样一些问题出现。在讲授第一章数学基础时，由于数学基础涉及统计概率、数学分析、矩阵论、最优化至少4门学课，所以所花的时间也不少，学生会有各种各样的困惑，有的学生会反问，难道机器学习基础就是让我们把数学重新复习一遍吗？有的学生会这样想，这么多的数学难道机器学习基础都用得上吗？其实这些数学都是用得上的，只不过学生还不知道即将用在什么地方，所以会产生这样的疑虑，后面讲到真正需要使用某一点数学的地方已经联想不起来了。专题式教学中则不会首先罗列一堆数学基础，而是以一个专题为单位，从具体问题的背景出发，建立理论模型，到理论推导，再到一类问题的解决，形成一个闭环体系。

线性回归模型是机器学习基础中最具有代表性、最简单的机器学习框架，教授好这个框架会起到以点带面的效果。下面就结合专题式教学法讲授其教学过程。

2.1 线性回归模型的起源

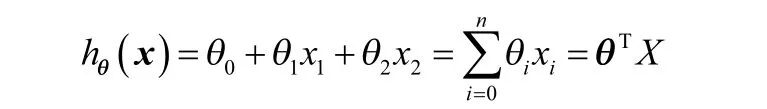
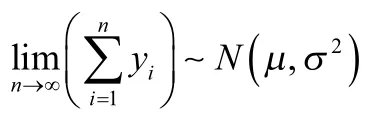
为了直观地验证中心极限定理，可以利用一门编程语言，这里利用Python模拟1 000个均匀分布的随机变量的和的分布情况，结果显示如图1所示。图1（a）是一个[0，1]均匀分布随机变量；图1（b）是1 000个这种均匀分布随机变量的和的分布，可以直观地看出，其为正态分布的曲线图。

2.2 线性回归模型的损失函数

J(θ)取最小值时对应的θ就是所要求的值。为了求到这个值，有相应算法，使用最普遍的就是梯度下降算法。这里不再展开该算法本身的教学探讨。至此，线性回归模型的框架已经建立，也就是从线性模型出发，寻找误差项的估计，利用中心极限定理，推导误差项的分布，得到每个样本的似然概率。根据样本的独立同分布的特性，得到样本集的联合分布，也就是θ的似然函数，最后线性回归模型的损失函数就悄悄浮出水面，推导过程自成一体，浑然天成。

3 讨 论

这种专题式教学方法，针对一个专题讲授与之相关的所有知识点和过程，非常符合当下的快节奏的学习方式，学生有强烈的所见即所得的体验和获得感。以线性回归模型这样一个简单的框架教学为例，传统的方法一般是直接给出损失函数，然后求解。虽然这个损失函数看似直观，但是背后的统计规律却没有讲清楚，学生听完不能以点带面，利用数学分布去思考其他模型。

专题式教学的第二个优势是现讲现用，知识的前后联系更加紧密，如果是自顶向下方法就是首先介绍数学分布、似然函数、中心极限定理等这样的数学基础，然后再讲线性模型。在没有讲到具体使用的地方，学生往往心生疑惑，究竟哪里能够用得上，甚至不知所谓。而专题式教学则避免这种情况发生，反而是让知识相互验证，印象更加深刻。均匀分布随机变量的和的分布Python代码如下：

专题式教学的第三个优势是让内容更加丰富多彩，机器学习模型中有很多数学推导，如果仅仅是过程推导会让教学变得枯燥，索然无味，如果配合相关的实践和图形展示，会让结果变得一目了然。在以上的线性模型的误差的分布估计时所讲的中心极限定理，可以用Python代码进行验证，结果显而易见，消除了公式的陌生感，而且也学会了一点儿程序实践，让过程推导变得图文并茂。

4 结 语

高等学校的专业教学非常重要，传统的教学方法有演绎式的自顶向下教学和归纳式的自底向上教学方法。本文着重探讨了专题式的教学方法，针对一个专题讲述与该专题有关的所有关联的知识，不需要前面大量的铺垫，在应用场景中现讲现用。这样做有显著的特点，即非常适合当下快节奏的学习，知识的前后联系更加紧密，容易理清来龙去脉，内容充实丰富；并且论证了该方法在机器学习基础教学中的应用，效果良好，受到学生好评。