二维BN中四种本征带电缺陷电学和磁学性质第一性原理计算*

刘雪飞,吕 兵，罗子江

(1. 贵州师范大学 物理与电子科学学院，贵阳，550025；2. 贵州财经大学 信息学院，贵阳，550025)

0 引 言

A.Zunger和合作者在1976年制备出厚度为(68.0±5.0) nm的六方氮化硼(h-BN)薄膜[1], 其测试结果表明h-BN为间接带隙半导体，带隙值为6.2 eV。20年后，有研究小组首次利用硼嗪在镍(Ni)(111)表面上的热分解反应制备h-BN单晶层[2]，开启二维h-BN的研究里程，该研究团队认为低维h-BN的带隙范围介于4.6 eV到7 eV，而且他们发现h-BN与衬底间的化学键较弱，从而使得h-BN电学性质几乎不受衬底影响，在温度高到1000 K 也能稳定存在。2004年石墨烯的成功制备并被证明具有优异物理性质之前[3- 4]，研究人员并没有意识到2D材料的优势，加之当时的制备工艺较差而无法制备出独立存在的二维材料。因此，大多数理论[5- 6]或实验[7-9]研究主要集中于h-BN/金属界面。直到2005年，Novoselov等人首次成功制备出独立存在的二维h-BN[10]。后来，随着技术的发展，Chunyi Zhi 等人报道一种利用超声波离心技术高产量制备二维h-BN，并证明h-BN可以有效改善高分子复合材料的热性能和力学性能[11]。另一个研究小组利用化学气相外延方法生长出两个原子厚度的大面积h-BN，其光学带隙为5.5 eV，并测试出其弹性模量为200～500 N/m范围[12]。随着工艺技术的不断进步，单层或少层h-BN的质量不断提高。然而，在制造h-BN的过程中，不可避免会引入空位、反位替换等点缺陷[13-14]。显然，这些缺陷将严重影响h-BN的物理性质。另外，为有意控制或改善h-BN的物理性质，需要在理论或实验上对二维h-BN中的空位、替代等点缺陷进行进一步的研究。Oba等人基于杂化Hartree-Fock密度泛函计算，通过插层法提出h-BN的双极性掺杂[15]。Wang等人在未修正形成能的情况下，计算单层和双层h-BN中4种点缺陷[16]，但会引入较大误差[17]。此外，作者在他们的研究中没有计算反位点缺陷(硼取代氮原子，反之亦然)。值得注意的是，由于二维材料中宿主波函数和缺陷波函数的量子限域效应，带电缺陷的作用与在三维体材料中的作用有很大的不同[17-18]。据我们所知，很少有文献用二维缺陷修正或外推的方法从理论上系统地研究单层h-BN中的4种本征点缺陷相关性质[15,18-26]。因此在我们发表的上一个工作中[27]，我们基于二维带电缺陷校正方法对二维h-BN中的4种本征缺陷的形成能和电荷转移能级进行系统计算，同时提出特殊真空层厚度可以进行缩放以及提出一种将局域密度近似下的(Generalized gradient approximation by Perdew John P., Burke Kieron, Ernzerhof ，GGA-PBE)下的电荷转移能级转化到杂化泛函(Heyd-Scuseria-Ernzerhof，HSE) 泛函精度的方法，然而关于带电缺陷的磁学和电学性质我们没有做深入讨论。因此，进一步深入讨论二维h-BN带电缺陷体系在各种价态下的磁学和电学性质非常必要。在本文中，我们首先计算本征h-BN 的电学和力学性质，然后计算了h-BN中4种本征缺陷：B空位(VB), N空位(VN), B反位(BN)以及N反位(NB)在最稳定价态下的电学和磁学性质，结合电子配位构型及自旋态密度解释了各价态下相应缺陷磁矩变化的机制。我们的研究结果对深入理解h-BN的缺陷性质具有一定指导意义。

1 计算参数及方法

基于第一性原理框架下GGA-PBE泛函[28]，赝势方法为投影增广波(projector augmented wave, PAW)[29]，所有计算均使用(vienna ab initio simulation package ,VASP)[30]。波函数基组截断能为400 eV，基于Monkhorst-Pack方法，倒空间K点采样密度为2×1×1，数据处理过程中，借助VASPKIT代码[31]和自编程序。结构优化过程中，原子上的Hellman-Feynman受力均小于0.1 eV/nm，能量收敛精度为10-6eV。图1(a)所示为计算中采用的6×6×1超胞，为避免非周期性方向上的伪相互作用，真空层厚度确定为3.0 nm。考虑到GGA-PBE方法会低估半导体材料禁带宽度，我们进一步使用杂化泛函(Heyd-Scuseria-Ernzerhof，HSE06)[32]能带进行修正计算。

图1 (a) 6×6超胞(144个原子)示意图，h-BN原胞被菱形描出，最小正交重复单元用矩形描绘出，4个本征缺陷用虚线圆圈标记；(b) 为h-BN原胞所对应的HSE投影能带图Fig 1 (a) Schematic diagram of 6×6 supercells (144 atoms). h-BN primitive cell is depicted by rhombus, the minimum orthogonal repeating unit is depicted by rectangle, and the four intrinsic defects are marked by dashed lines and circles; (b) The HSE projection energy band structure corresponding to h-BN primitive cell

2 结果与讨论

2.1 h-BN 基本性质计算

在进行带电缺陷计算之前，我们首先对完美的h-BN进行基本性质计算，采取的计算原胞用菱形描绘在图1(a)中，原胞计算的K点采样密度为23×23×1。经过优化，h-BN的晶格常数为0.25 nm，键长为0.145 nm，与文献中的结论[33]一致。图1(b)为原胞h-BN所对应的HSE 投影能带图，从能带图我们可以看出h-BN属于间接带隙半导体，价带顶在K点，而导带底在Γ点，其对应的带隙宽度为5.67 eV。另外，我们发现价带顶主要由N原子p轨道贡献，而导带底则主要由N原子的s轨道贡献。我们进一步计算了h-BN带边有效质量，发现电子有效质量沿K->M和K->Γ方向分别为1.08 和0.79 m0，空穴有效质量则分别为0.52 和0.66 m0，其中m0为电子质量，说明载流子有效质量具有一定各向异性。接着我们计算h-BN的力学性质，力学量主要涉及弹性模量Yk(GPa.nm，N/m，k=x，y)，刚度系数Cij(GPa·nm，N/m，i，j=1，2，6)，泊松比以及剪切模量S(GPa·nm，N/m)。二维结构中应变及应力之间的数学关系可由下式决定：

(1)

其中Cij可表达为：

(2)

S0是h-BN晶胞的x-y面积，应变能Es为：

(3)

应变由ε=(L-L0)/L决定，其中，L0和L分别为施加应变前后的晶格常数。应变施加范围从-2.5%到+2.5%，应变增量取0.5%，使用VASPKIT进行拟合得到弹性常数，从而求出杨氏模量和泊松比[34]：

(4)

(5)

计算表明h-BN弹性模量Yx(Yy)为和275.92(N/m)，与文献[35]报道结果非常接近。

表1 h-BN剪切模量S(GPa·nm，N/m), 弹性常数Cij(GPa·nm，N/m，i，j=1，2，6)，泊松比υk，k=x，y,弹性模量Yy(GPa·nm，N/m，k=x，y), 电子有效质量(me*/m0*)，空穴有效质量(mh*/m0*)Table 1 Calculated elastic stiffness constants Cij(GPa·nm,N/m),i,j=1,2,6, elastic’s modulus Yk(GPa·nm,N/m),k=x,y,Shear Modulus S(GPa·nm,N/m) and Poisson’s ratio νk,k=x,y are presented. Effective mass of electrons (me*/m0*), effective mass of holes (mh*/m0*)

2.2 h-BN 本征缺陷结构性质

对h-BN二维结构的基本物理性质进行讨论以后，我们将六方原胞进行正交化，并进行扩胞(6×6)，然后依次引入4种本征缺陷，计算了各种缺陷在-3价到+3价带电态下的磁学和电学性质。在我们前期发表的工作中，发现对于4种本征缺陷并非所有价态都是稳定的，因此我们只讨论最稳定价态(most stable charge states, MSCS)，关于最稳定价态的定义已经在我们发表的工作中[27]有详细说明，在此不再赘述。另外，进过优化，我们统计出各缺陷体系中远离(Far，F)和靠近(Near, N)缺陷位置的B-B，B-N，N-N键长，总结在表2中。

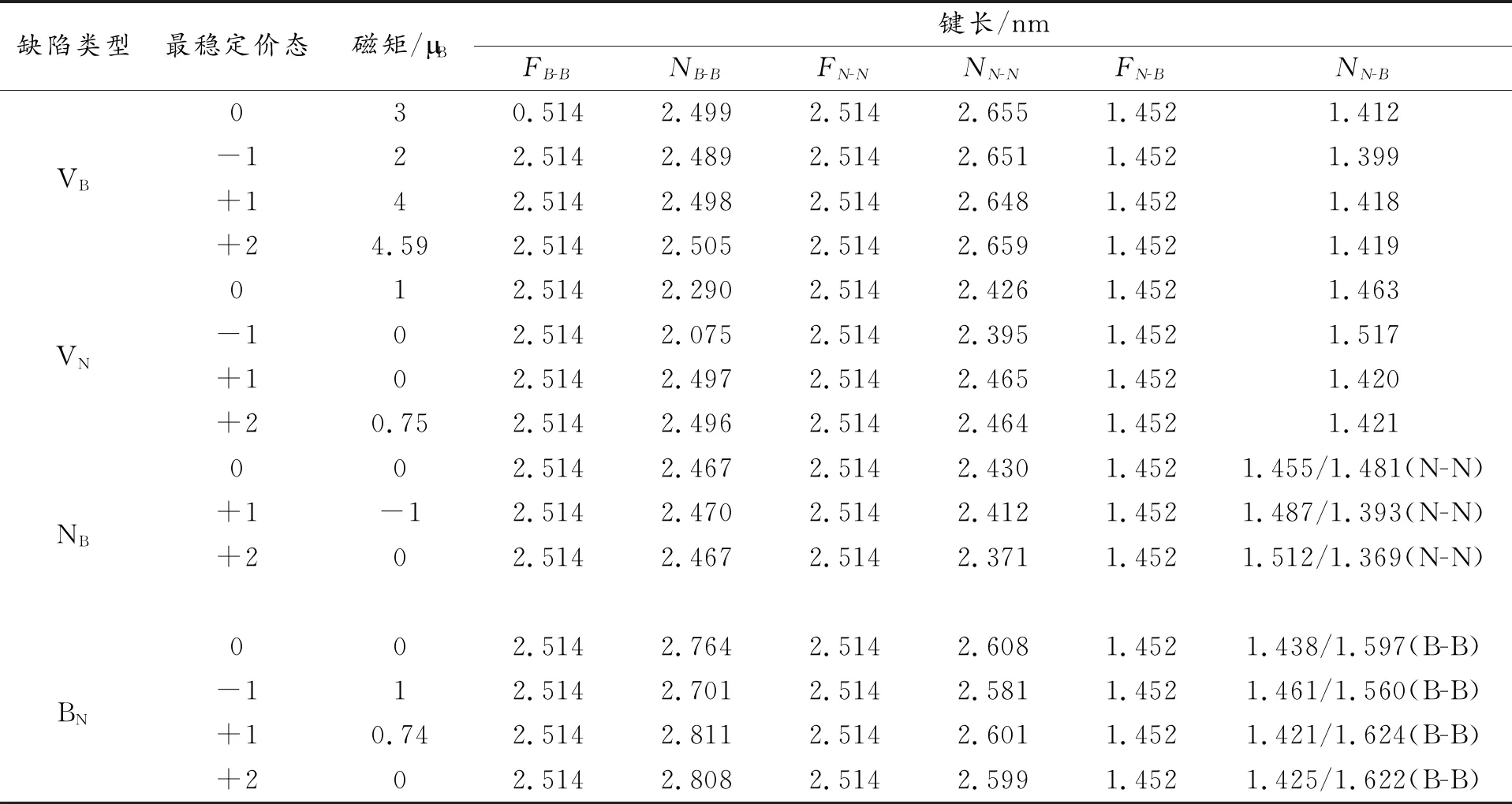
表2 最稳定价态下各缺陷附近的键长及磁矩(Mm)信息Table 2 The bond length and magnetic moment (Mm) around each defect in the most stable valence state (MSCS)

从表2数据可以看出对于VB体系，缺陷附近的B-B键和B-N键有微弱减小，而N-N键增大了5%左右；对于VN体系，缺陷附近的B-B键和N-N键较VB体系变小，说明VN体系比VB体系相对更加稳定。需要注意的是在VN附近的B-B键在+1 和+2价态有微弱减小，但在-1价和中性价态显著减小，而N-N和N-B键在各价态中则没有太大差异；对于NB体系，B-B键变化很小，而B-N和N-N键变化相对较明显；对于BN体系，3种键长都有所增大，且正价态增加更加明显。这些丰富的键长变化规律是由于体系引入缺陷后电子密度的重新分布所致。

图2所示为h-BN本征缺陷体系处于中性价态时的电荷密度分布。对于VB体系，在z方向结构未发生畸变，表明sp2杂化特点被保留，因而结构仍然维持平坦。另外，B-N和B-B键长几乎保持不变，而N-N间距则因库伦排斥作用而被拉长，结果与文献[37]一致。对于氮空位体系，缺陷附近B-B 和N-N 键长相比VB体系变小，这是由于缺陷诱发的硼原子间较强的吸引作用。需要强调的是，+1，+2价态时，B-B键变化较小，而在-1价态和0价态时，则明显变短。对于氮占据硼原子反位缺陷体系，B-N键由于较强的库伦作用而变长，B-B 和N-N键长则变化微弱。相比之下，BN体系中N-B键具有离子键特性， B-B键具有共价键特性，类似于文献[38]中研究结论。另外，BN体系中B-B和N-N键分别增大了0.025 和0.01 nm，而B-N键则几乎没变化。总体来说，具有负价态的BN体系缺陷体系键长小于正价态缺陷体系，表明该体系处于负价态时相对更稳定。

图2 中性价态h-BN中各种缺陷电荷密度Fig 2 The charge density of four native point defects in neutral charge states

2.3 h-BN本征缺陷电学和磁学性质

接下来我们将以VN体系为例进一步讨论这些缺陷体系的电学和磁学性质，对于h-BN, 在中性态时，该缺陷体系磁矩等于1B，而±1价时则无磁矩，在+2价时磁矩等于0.75B。这些丰富的磁矩变化规律，可根据其成键过程进行解释，如图3所示。

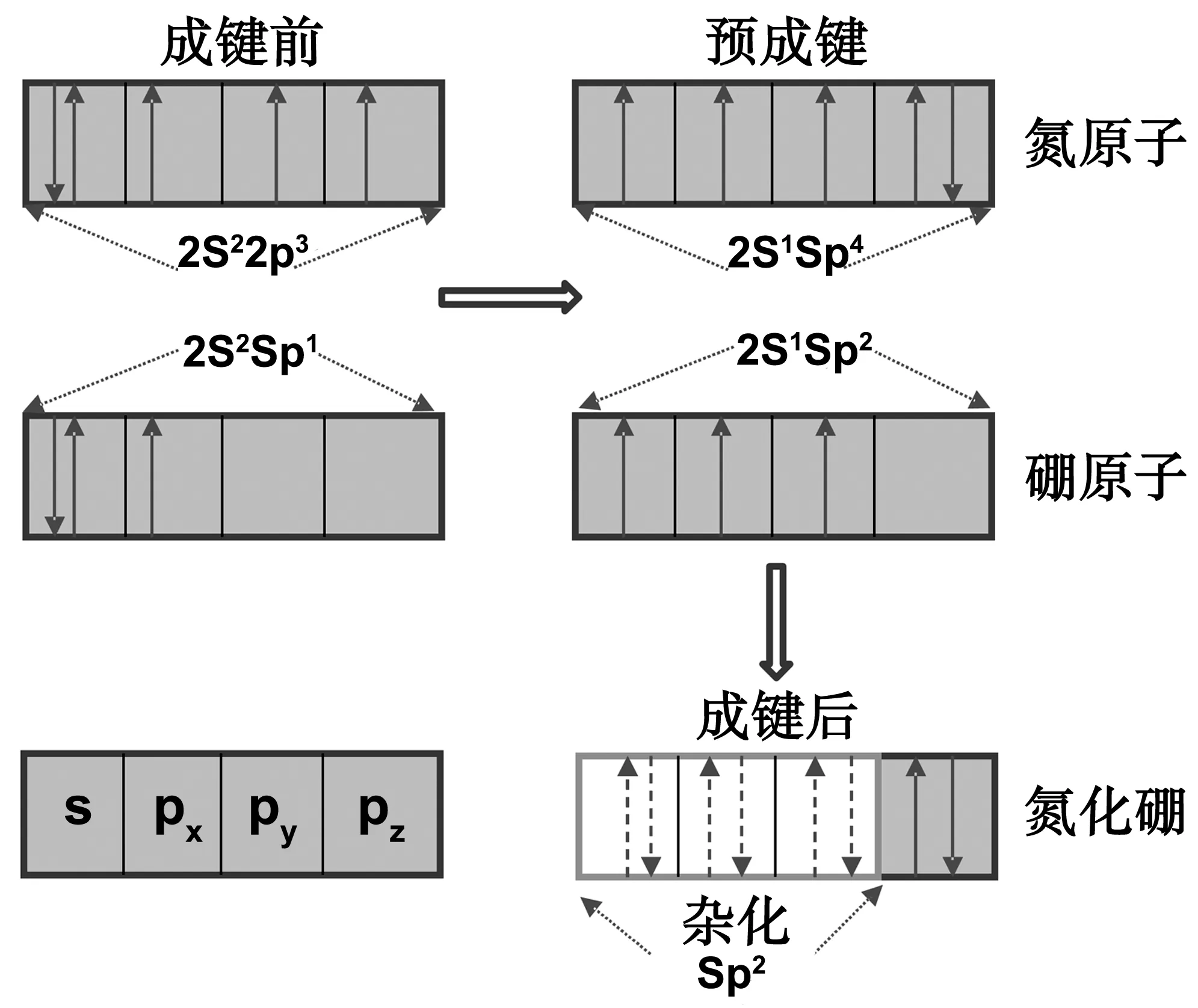
图3 h-BN中氮空位缺陷系中电子配位结构示意图Fig 3 The schematic of electron configuration of VN system in h-BN

二维氮化硼中氮原子(硼原子)电子构型在成键前是2s22p3(2s22p1)，B-N成键过程中，B 中1个s轨道电子被激发到其p轨道，形成2s12p2排布，类似的，N电子构型更新为2s12p4，根据泡利不相容原理，其中硼两个p轨道电子成对，B p和s轨道剩下的孤立电子将与N相应轨道孤立电子重新组合形成sp2杂化轨道，因此h-BN成平坦结构。sp2杂化轨道模型表明无单电子出现，因此h-BN磁矩为0B，然而，当h-BN存在N空位缺陷时，B电子构型变为2s22p1， 因此p轨道中单电子导致其磁矩为1B，体系得到或失去一个电子后，使得电子重新成对，其磁性将消失。其它体系可做类似讨论，在此不在详细展开。

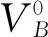
3 结 论

基于第一性原理方法，本文首先计算了二维h-BN材料的本征电子结构，带边载流子有效质量以及力学性质。其中h-BN的带隙值为5.67eV, 为间接带隙半导体，其价带顶由N原子p轨道贡献，而导带底则由N原子s轨道贡献。发现电子有效质量沿K->M和K->Γ方向分别为1.08 和0.79 m0，空穴有效质量则分别为0.52 和0.66 m0，说明载流子有效质量具有各向异性。力学性质显示其弹性模量在x和y方向均为275 N/m，泊松比均为0.23，显示其力学性质具有各向同性。在此基础上，我们进一步对h-BN中4种本征缺陷的稳定价态的结构性质进行计算，总结出缺陷附近及远离缺陷的键长变化规律。然后对各稳定价态下缺陷电学和磁学性质进行深入讨论，结合电子配位构型以及电子自旋态密度解释了缺陷在不同价态下产生不同磁矩的机制。