改进三维不规则排样构造算法

刘 虓，徐 磊，陈超核，刘嘉敏

(1.华南理工大学 土木与交通学院，广东 广州 510640；2.沈阳工业大学 信息科学与工程学院，辽宁 沈阳 110870)

0 引言

三维排样是在三维空间将多个零件在容器内进行优化布排的过程[1-5]，在船舶/航天器舱室布局设计、集装箱装运、激光烧结等领域有广泛应用。排样问题作为一类典型的优化问题，其 “设计变量”为零件排样次序；“目标函数”为零件在容器内的排布密度；“约束条件”为零件之间以及零件与容器之间不重叠/冲突。将零件依次排入容器并计算排布密度的算法称为排样“构造算法”(constructive algorithm)，因此构造算法也可看作目标函数的“求解器”。规则三维排样算法已较成熟[5]，不规则排样算法则处于前沿阶段[1-4]。三维不规则零件几何要素和运动自由度较多，相应的构造算法计算效率很低，已经成为三维不规则排样的瓶颈，有必要对其进行更广泛和深入的研究。

构造算法的核心包括零件可行域构建和零件重叠检测两个。临界多边形(No Fit Polygon, NFP)是构建二维排样[6]可行域和避免零件重叠的通行工具[1]，但NFP的生成算法比较耗时，如果将NFP推广到三维，所谓“临界多面体”的生成算法将更加复杂。此外，NFP在考虑零件旋转时会进一步增加算法耗时。因此，很多学者另辟蹊径，提出两类方法：①“像素”方法，Stoyan等[7]将零件分解成多个长方体，将两个零件之间的距离计算在两组长方体之间展开；②“矢量”方法，基于最小势能原理的三维排样启发式算法(Heuristic Algorithm based on the principle of minimum total Potential Energy for 3D packing problems, HAPE3D)[8-9]采用多面体表达零件，将重叠检测归结于“点与线”以及“线与线”的几何关系判断。HAPE3D的优点是：零件定位精确、旋转方便;缺点是：①零件顶点数较多时，算法开销大；②零件只能绕3个坐标轴旋转，实际上对零件的可行域进行了不必要的限制。

SAT等[10]在二维排样问题中，尝试将零件像素化表达，提高了零件重叠检测的效率。本文则在三维排样问题中将“像素化”和“矢量化”方法进行混合，扬长避短，很好地解决了HAPE3D的缺点①。全姿态(all attitude)主要用来描述航空、航天领域对象在空间中的方位姿态[11-12]。方位姿态的描述包含两组要素：①航向角、俯仰角和横滚角；②机体坐标系与地理坐标系之间的关系。HAPE3D没有考虑第二组要素，这是产生缺点②的根本原因。本文将“全姿态”概念引入三维排样，摆脱了零件只能绕坐标轴旋转的束缚，实现了全方向、多角度的“自由”旋转。

1 概念和预备知识

1.1 零件微粒

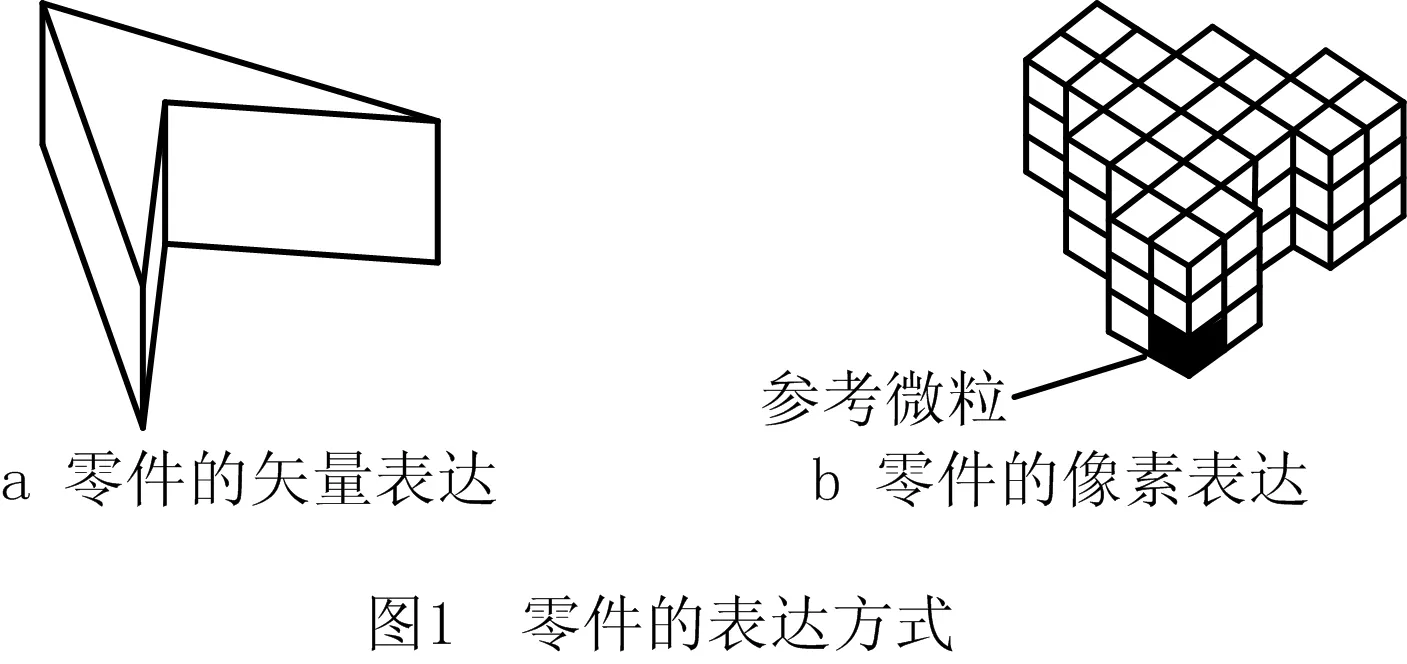
采用多面体“矢量化”表达的零件(如图1a)使用边长为PSL(particle side length)的方块微粒(particle)进行填充，即变为 “像素化”表达(如图1b)。如图1b中的黑色方块所示，可任选一个微粒作为参考微粒 (Reference Particle，RP)，零件的平移和旋转均基于RP。

1.2 排样块

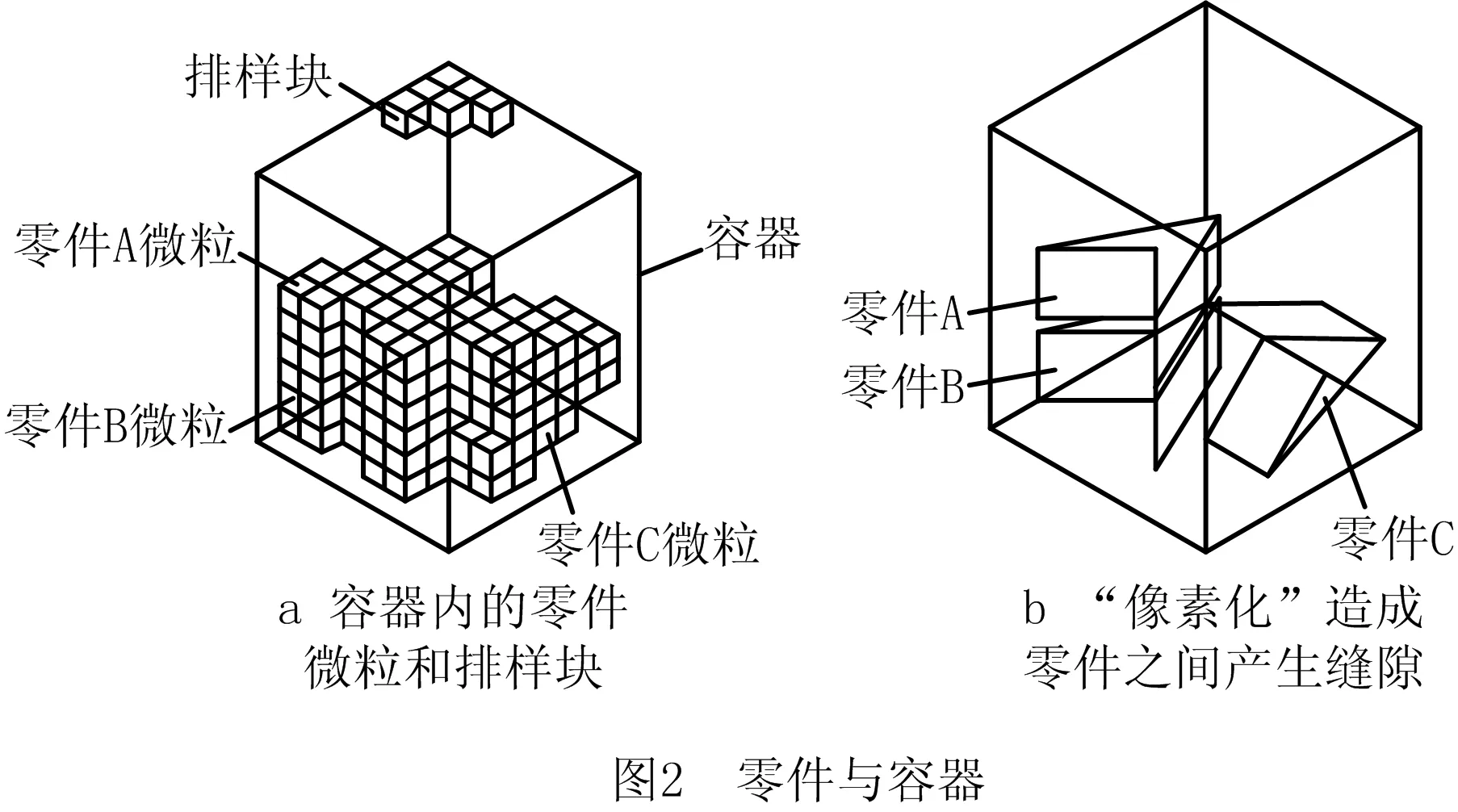
与零件“像素化”类似，也可用方块填充容器(如图2a)，该方块称为排样块 (Packing Block, PB)，其边长BSL (packing block side length)=PSL。为方便观察，图2a只绘制了容器上端一隅6个排样块。为了重叠检测，设置布尔变量BlockOccupied作为排样块的占用标志，其初始值为“空”：BlockOccupied[j]=false，其中j=0,1,…,BN-1(BN为排样块个数)。排入零件后，部分排样块被零件微粒“占据”：BlockOccupied[j]=true。

1.3 “分离”判断

如零件在容器内，且与其他零件“分离”，则其排样姿态“可行(Feasible)”。文献[9]基于矢量图将零件的分离判断归结于点与多面体的包含关系以及线段与面的相交关系，随着零件几何要素(点、线、面)的增多，该分离判断变得非常耗时。本文提出基于最小势能原理和混合图形的三维排样启发式算法(HAPE3D_Hybrid Representation Graphics, HAPE3D_HRG),将零件重叠检测归结于零件微粒和排样块之间是否重叠的布尔运算。显然，基于布尔运算的重叠检测更为简单、高效，大大提高了构造算法的执行效率。

1.4 “靠接”算法

零件和容器“像素化”之后，有可能在排入零件之间产生空隙(如图2b)，可以通过“靠接”算法消除之。

两个零件A、B分离，A固定，B向A靠拢直至接触(但不重叠)，该过程称为零件的靠接[9]，如图3所示。为保证足够的精度，靠接算法需要零件为“矢量化”表达。

1.5 全姿态(all-attitude)

全姿态(all-attitude)在航空航天领域用来描述飞机、导弹和卫星的姿态。本文将其加以改造并用于三维排样。

如图4所示，零件姿态包含两个要素：①零件局部坐标系zL轴的指向；②零件绕zL轴的旋转角。

(1)zL指向的确定方法

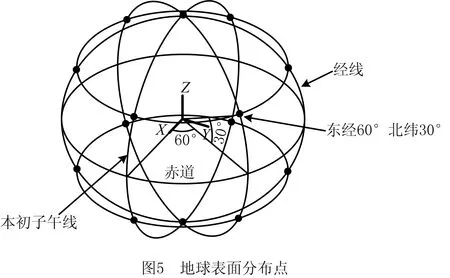
如图5所示，以地球中心为起点，球面某点为终点，即可确定zL指向。设定正整数RN(Rotation Number)，就可在球面布置多个点作为zL的终点，步骤如下：

步骤1沿经线从南极到北极经过180°，分为RN等份，可确定RN+1个等分点。

步骤2沿纬线从本初子午线向东出发，直至回到原点，经过360°，共分为2RN等份，可确定2RN个等分点。

步骤3综上共有2RN(RN+1)个分布点，另考虑到南北极各有2RN个点是重复的，故分布点个数为：

2(RN2-RN+1)。

(1)

当RN=3时，球面上有14个分布点(如图5)。

(2)零件绕zL轴的旋转角

如零件绕zL轴旋转2RN个角度，即每隔180°/RN旋转一个角度，则每个分布点对应2RN个姿态。如图5所示，假设RN=3，从球心到东经60°、北纬30°分布点可以确定某个zL轴，零件绕其旋转可以确定6个姿态，如图6所示。

考虑到式(1)，零件姿态个数AN为：

AN=4RN(RN2-RN+1)。

(2)

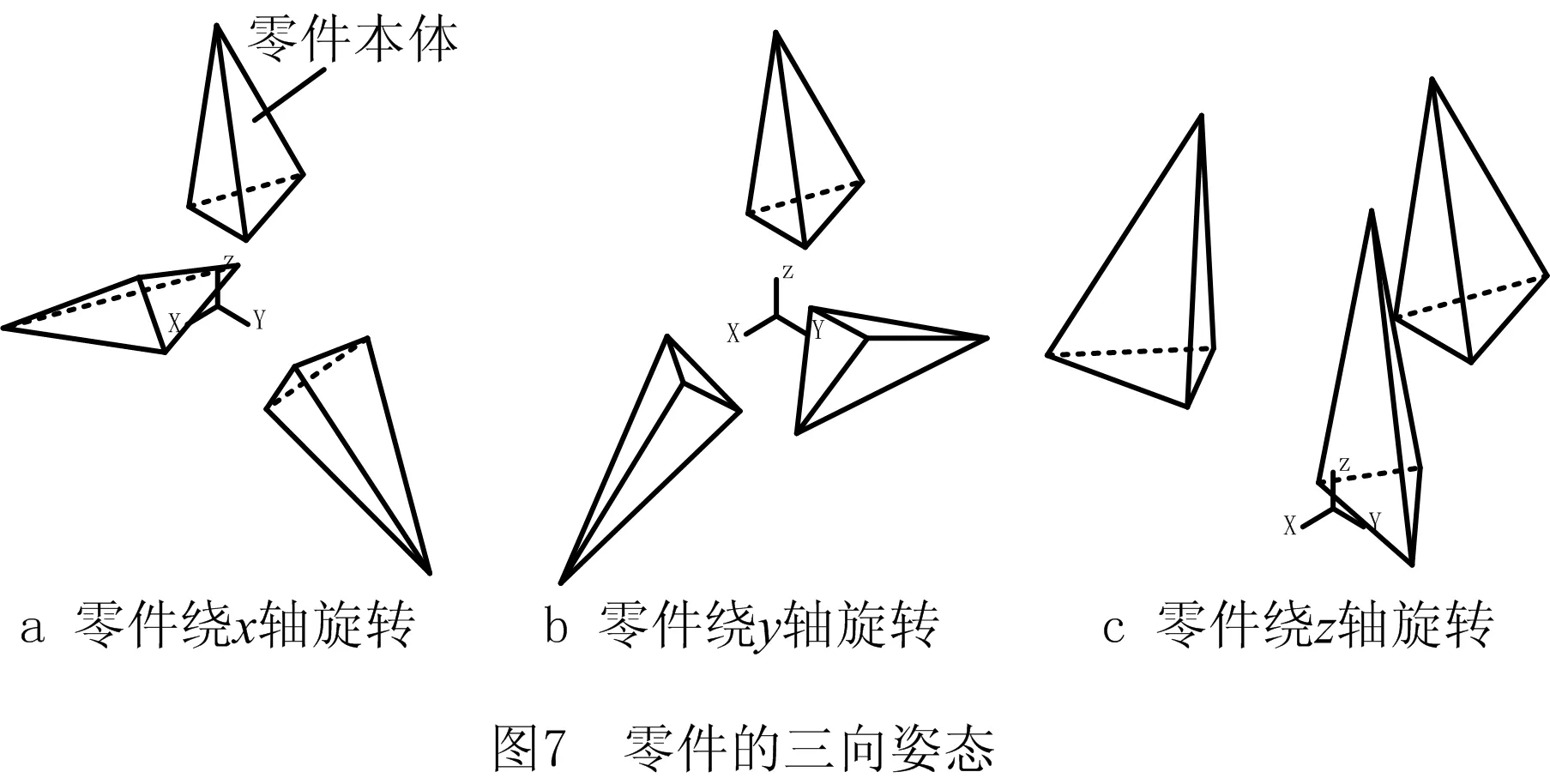
三向姿态[9]下，零件绕x、y、z轴旋转RN个角度。当RN=3时，三向姿态只具备9个姿态,如图7所示。

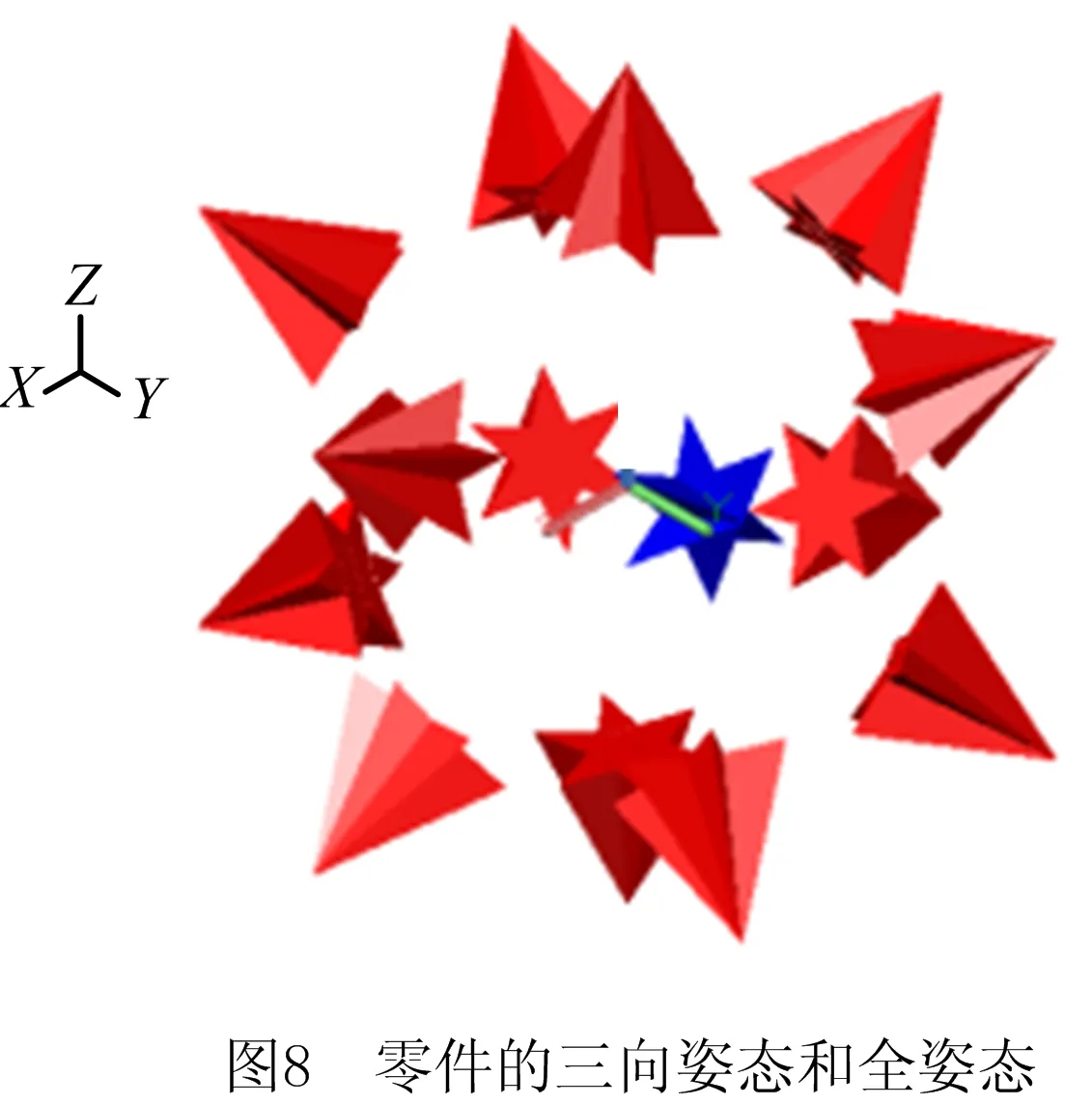
“全姿态”下，零件在14个方向上共有84个姿态(如图8)。理论上，只要RN足够大，“全姿态”可以充分考虑零件姿态的各种可能，从而令构造算法更有可能在容器空间找到更为优化的姿态。

2 算法描述

零件在容器内的运动遵循“最小势能原理”：零件总是试图通过平移和旋转降低其重心高度，从而得到更加紧密的排列[9]。本文在HAPE3D基础上利用混合表达图形(Hybrid Representation Graphics, HRG)提出了一种改进三维排样构造算法(HAPE3D_HRG)，算法流程如下：

(1)为所有零件指定某种排样次序(比如按照零件体积大小排序)。

(2)多个排样块PB完全充满容器(PB边长为BSL)，令所有排样块处于“空置”状态。

(3)按照既定排样次序选择某个零件作为当前待排零件。

(4)确定当前零件AN个姿态：Attitude[i] (i=0,1,…,AN-1)。

(5)某个姿态下，当前零件分解为多个微粒(微粒边长PSL=BSL)，任选一个作为参考微粒RP。

(6)零件访问BN个排样块PB[j](j=0,1,…,BN-1)，即零件平移直至RP与PB[j]重合。

(7)找到最优可行排样姿态(在此姿态下，零件重心高度最低，且零件微粒与排样块不冲突)。

(8)因为零件和容器分别被微粒和排样块“离散”，当前零件有可能与“已排”零件之间存在空隙(如图2b)，可用 “靠接”法[9](如图3)消除之(靠接之前零件恢复为“矢量化”表达)。

(9)与当前零件冲突的排样块置为“被占据”。

(10)如果还有待排零件,则返回步骤(3)。当所有零件完成步骤(3)～步骤(9)，则HAPE3D_HRG结束。

步骤(3)～步骤(9)为单个零件的排样，具体实现如图9所示。

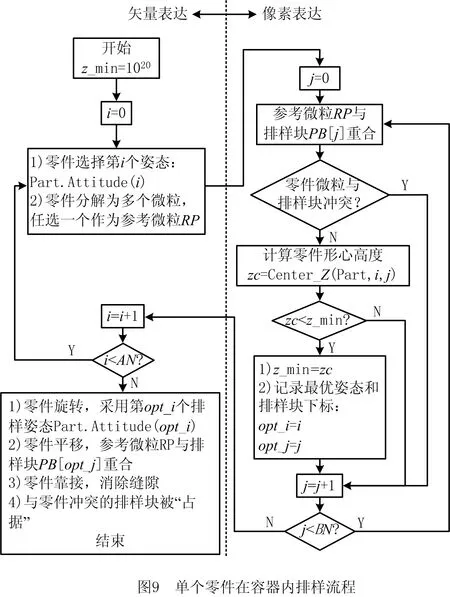
在步骤(1)～步骤(4)之间，所有零件采用“矢量化”表达;步骤(5)～步骤(7)之间， “待排”零件采用“像素化”表达(如图9虚线右侧)，零件重叠检测由过去复杂的几何关系计算[9]转化为零件微粒和排样块之间是否冲突的逻辑判断，这正是算法速度提升的关键所在; 从步骤(8)开始，待排零件恢复为“矢量化”表达，以方便零件的靠接[9]，也保证了构造算法在后期能够输出精确的排样图并计算排样密度。

3 算例

为了对HAPE3D_HRG进行算法验证和对比，本文编写了程序(http://www.huagongchuanhai.cn/packing/)，进行了两组算例研究。算例1研究零件表达对于计算速度的影响，由于零件的旋转方式也会影响算法速度，算例1限制了零件的旋转;算例2则用来测试HAPE3D_HRG的综合表现，并与国外同类算法进行比较。

3.1 算例1

文献[7]中多面体算例有10种零件类型(如图10)，每种零件的数目为n。令n从2～5取值，共进行4组实验(零件不允许旋转)。表1中，零件总数N=10n：第1组n=2，零件总数N=20；第2组n=3,零件总数N=30，…，依此类推。文献[9] (PC主频3.1 GHz，排样点距PPD=1.0 mm)使用HAPE3D基于矢量图得到的排样密度和时间分别列于表1第3、4列。本文(PC主频3.0 GHz， BSL=1.0 mm)编程实现HAPE3D_HRG算法，进行了同样的实验(如图11)，排样密度和时间分别列于表1第5、6列。图11中：l、w和h分别为容器的长、宽和零件排样高度(单位：mm); 排样密度=所有零件体积/(l×w×h)。

表1 HAPE3D[9] (主频3.10 GHz)与HAPE3D_HRG(主频3.0 GHz)排样密度和时间对比(零件不旋转)

如图11所示，HAPE3D_HRG可处理不规则三维零件，并具备孔洞填充功能。如表1第3列、第5列所示， 在零件不允许旋转的情况下,新老算法的排样效果基本相当，但后者的计算效率有了显著的提升。如表1最后一列所示，HAPE3D_HRG对老算法的加速比最低为4.24，最高为10.64，平均加速比为8.43(已考虑PC主频差异)。

3.2 算例2

为了进一步测试HAPE3D_HRG的综合性能，令零件全姿态旋转(RN=4)，利用HAPE3D_HRG作为目标函数(排样密度)的求解器，以零件排样次序为设计变量，以模拟退火算法SA为迭代优化方法，最终得到的排样图如图12所示。作为参照，同样将HAPE3D与SA进行搭配，得到排样图如图13所示；另外还将Romanova等[3](主频2.7 GHz)的排样结果列于图14中。3组对照实验的排样密度和时间如表2所示。

表2 HAPE3D_HRG+SA(主频3.0GHz)、HAPE3D+SA(主频3.0GHz)、COMPOLY[3] (主频2.7GHz)排样密度和时间对比

由表2可得以下3点结论：

(1)在前3个算例的比较中，本文算法所得排样密度最好。

(2)HAPE3D+SA的计算时间比本文算法要短很多，这是因为在RN=4的前提下，前者只考虑零件绕x,y,z三个坐标轴的旋转，即一共考虑4×3=12个姿态；而根据式(2)，本文算法在全姿态条件下，要考虑208个姿态。

(3)在排样密度相当的前提下，本文算法的迭代时间比COMPOLY要短得多(已考虑PC主频差异)。

4 结束语

本文提出一种改进的三维不规则排样构造算法HAPE3D_HRG，并做了两个方面的工作：

(1)在重叠检测阶段，零件由矢量表达变为像素表达，从而将复杂的几何算法转为简单的布尔运算。整体算法效率提升显著。

(2)零件以“全姿态”旋转，大大扩展了零件姿态的寻优空间。实验证明HAPE3D_HRG是一个性能优良的构造算法，将其作为目标函数的“求解器”，可令优化迭代在更短的时间内搜索更大的可行空间，从而有可能得到更优的排样结果。

目前本文只将HAPE3D_HRG与模拟退火算法结合进行了初步的研究，与别的优化算法(遗传算法、人工神经网络等)将会擦出怎样的“火花”？这是未来值得研究的课题。此外，零件由矢量表达转为像素表达后，像素越精细，排样效果越好，但同时也会增加存储和计算的负担。如何在排样效果、存储空间以及计算效率之间进行平衡，也需要在未来继续展开研究。