一种指数形式时变加权的机载双基雷达STAP算法*
赵 军,吴 迪,沈明威,朱岱寅
(1.空军工程大学 航空机务士官学校 雷达成像与微波光子技术教育部重点实验室,河南 信阳 464000;2.南京航空航天大学 电子信息工程学院,南京 210016;3.河海大学 计算机与信息学院,南京 211100)
0 引 言
机载双基地雷达具有作用距离远、抗干扰能力强、反截获性能好等优点,并且通过收发分置在提高战场生存能力和隐身目标探测方面具有独特优势[1]。但采用收发分置后,由于收发平台同时运动,使得地面杂波的多普勒频率展宽比单基条件下更加严重,地面慢动目标被广泛分布的杂波“淹没”,造成雷达系统的动目标检测能力严重下降。空时自适应处理(Space Time Adaptive Processing,STAP)技术采用空域和时域信息联合处理进行二维自适应滤波,实现地面杂波有效抑制[2]。经过四十多年的研究发展,STAP技术在单基雷达的应用研究已较为成熟,双基雷达STAP技术受到了广泛关注。
为适应复杂多变的外部环境,STAP技术需要从待检测单元两侧选取相邻距离单元的杂波数据进行协方差矩阵估计。为确保估计的有效性,相邻距离单元的杂波必须是独立同分布(Independently and Identically Distributed,IID)样本[3]。机载双基雷达收发分置的特殊结构导致杂波产生距离依赖性,各距离单元杂波不再是IID样本,由此训练出的滤波器凹口变宽变浅,不仅造成杂波抑制性能急剧下降,而且会把与杂波相邻的慢动目标直接滤除。因此,双基STAP技术应用首先要解决杂波的距离依赖性问题。
减小或消除机载雷达杂波距离依赖性的方法有三类:一是局域处理类,包括局域联合处理法(Joint Domain Localized,JDL)[4]、三通道先时后空自适应级联处理法(3 Doppler Time Space Adaptive Processing,3DT-SAP)[5]等。该类方法通过减少训练样本的数目以降低杂波非均匀程度,但协方差矩阵的有效估计需要足够多的样本才能保证,两者的矛盾使得该方法性能急剧下降。二是杂波补偿类,包括角度-多普勒补偿(Angle Doppler Compensation,ADC)法[6]、多普勒频移(Doppler Warping,DW)法[7]。该类方法通过杂波补偿使各训练样本在某一点重合。但该类方法需要精确知道雷达工作参数和载机运动信息,受载机惯导系统误差影响较大,而且增加了运算复杂程度。三是权值扩展类,主要包括时变加权(Time-Varying Weighting,TVW)法及其改进非线性TVW(Nonlinearly TVW,NL-TVW)法[8-10]等。该类方法无需知道载机的参数和几何配置,直接对样本数据进行扩展。但TVW法假定自适应权矢量随距离的线性变化,而且变化速度保持不变,这与真实情况不符。
针对以上问题,本文在分析双基杂波非平稳特性和TVW法不足的基础上,提出一种基于指数形式时变加权(Exponent TVW,ETVW)的STAP算法。该方法采用距离的指数函数来表示最优权矢量的非线性变化,可以有效补偿杂波的距离非平稳,在不同距离条件下都能有效抑制双基杂波,性能优于原有的权值扩展类方法和局域处理法。
1 双基杂波的非平稳特性
建立空间直角坐标系如图1[11]所示,发射平台位于TX且飞行高度为HT,接收平台位于RX且飞行高为HR,基线长度为收发平台之间的距离L,发射平台以速度vT沿与基线夹角为αT的方向运动,接收平台以速度vR沿与基线夹角为αR的方向运动。雷达发射脉冲经过距离RT到达地面散射点P,经反射后到达接收机,行程为RR,收发距离之和为RS。发射、接收波束指向相对于基线方向的方位角分别为θT和θR,发射、接收波束指向相对于地面的下视角分别为φT和φR,发射、接收平台相与杂波散射点P的锥角分别为ψT和ψR。
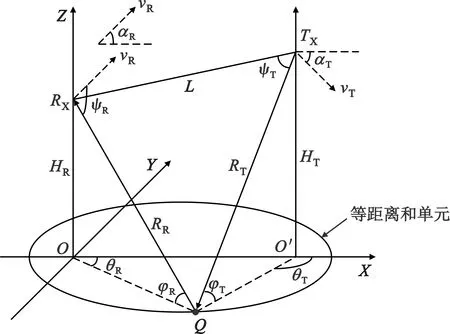
图1 机载双基雷达几何关系
回波信号的多普勒频率
(1)
根据图1的几何配置关系,得到
(2)
(3)
将式(2)~(3)代入式(1),建立多普勒频率fd与空间锥角cosψR的关系式,进而得到杂波轨迹在2fd/fr~cosψR平面内的空时分布。选取三种典型几何配置,如图2所示,图中飞行方向的方位角为45°的整倍数。
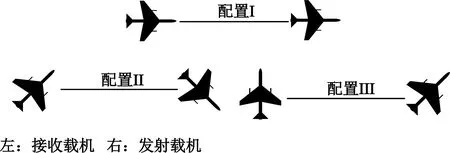
图2 双基典型场景示意图
对距离和分别为50 km、100 km和150 km条件下杂波轨迹的空时分布。考察表明,在各种配置下机载双基雷达杂波分布产生距离依赖性,不同距离下杂波轨迹不同,杂波距离向分布非平稳。此外,杂波轨迹在近距离单元之间变化越剧烈,在远距离单元之间变化平缓直至趋于收敛,具有“先快后慢”的特点。
STAP处理器最优的前提是各距离单元杂波满足IID条件,机载双基雷达杂波分布的非平稳特性将导致杂波不满足IID条件,由此可知STAP处理器的杂波抑制性能显著降低。
2 时变加权法
2.1 杂波非平稳对STAP的影响
假设机载双基雷达有N个接收通道,相干处理间隔内包含K个脉冲,经STAP处理器作用后第l个单元的输出
Y(l)=wH(l)x(l) 。
(4)
式中:x(l)是第l个距离单元的样本数据矢量,w(l)为NK×1维STAP最优自适应权矢量,满足
(5)
式中:Rl=E[x(l)xH(l)]表示由接收杂波和噪声的协方差矩阵,s表示NK×1维空时二维导向矢量,()H表示共轭转置,μ为归一化常数。
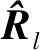
(6)
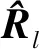
而双基杂波距离向分布具有距离依赖性,不同距离单元杂波轨迹的空时分布各不相同,这与训练样本满足IID条件的假设矛盾,大范围采集训练样本将导致杂波分布在空时平面扩散,协方差矩阵估计误差增大,STAP处理器的杂波抑制能力下降。
2.2 时变加权算法
为解决非平稳条件下STAP杂波抑制问题,麻省理工学院林肯实验室的Zatman博士[8-9]提出了时变加权的方法。该方法假设STAP处理器的最优权矢量与距离相关,是距离的线性函数。设检测单元为第0单元,训练样本从其左右两侧各取L个距离单元,第l单元的最优权矢量w(l)满足
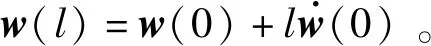
(7)
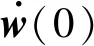
由于式(7)中只包括有距离单元l的一次项,因此TVW算法的假设前提是把权向量看成距离的线性函数,但这与双基杂波分布的真实情况不符。一方面,权矢量w(l)是距离单元数l的线性函数,这表明在所有距离单元w(l)变化的速度相同,但由前面分析,双基雷达的杂波分布不同距离单元变化的速度不同,在近距离单元变化剧烈,在远距离单元变化平缓,其权矢量变化也应符合这种“近快远慢”的规律。另一方面,将w(l)进行展开时,只考虑了一次项,而忽略其二次及其以上项的影响,造成该方法误差较大。NL-TVW法[9]虽然考虑了二次项的影响,但随着l增大,其权矢量不收敛,因此需要对现有的方法进行改进。
3 指数时变加权算法
机载双基雷达杂波分布在近距离变化剧烈,在远距离变化缓慢,究其原因是电磁波在大气传输中的衰减造成的。
由于雷达信号的传播衰减符合负指数函数的规律:
f(x)=e-αx,α>0 。
式中:α表示衰减系数,x表示信号传播距离[12]。基于以上分析,我们在TVW算法的基础上提出一种指数形式的ETVW法。
ETVW算法认为双基STAP的最优权矢量w与距离单元l的指数函数有关,满足
w=w(e-αl) 。
(8)
根据Taylor公式,将w(e-αl)展开并忽略其三次及以上项得
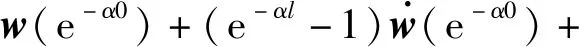
(9)
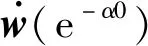
第l个单元的STAP处理器输出
Y(l)=wH(e-αl)x(l)=
(10)
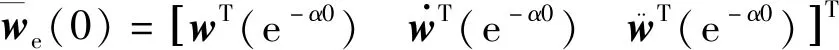
对于指数扩展后样本,此时STAP最优权矢量
(11)
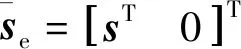
(12)
式中:μ1和μ2为归一化系数,它们保证当回波数据为白噪声时,由扩展数据估计出来的杂波协方差矩阵为单位阵。μ1和μ2分别满足
(13)
(14)
考虑归一化系数作用后的扩展样本数据表示为
(15)
由式(15)看出,经ETVW算法扩展后,处理器的维数由2NK增加到6NK,训练样本的数目扩大为原来的3倍,运算量也由o[(NK)3]增加到o[(3NK)3],如此大的运算量和样本个数在实际过程中是难以接受的,这里采用3DT-SAP法进行降维处理[2,5],以降低运算量,减少训练样本数目。
4 仿真分析
仿真场景选取图2中几何配置I,雷达系统参数如表1所示。
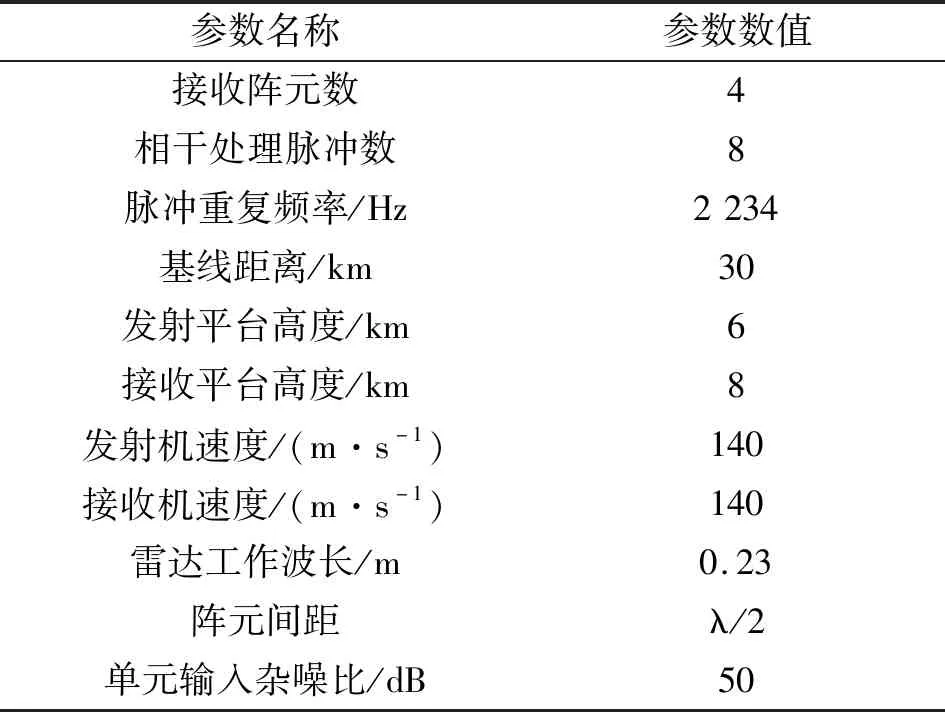
表1 雷达仿真参数
根据文献[9-10],当双基距离和超过基线距离的5倍时,认为杂波处于远距离单元,分布是平稳的。仿真中基线长度L=30 km,因此,当雷达信号传播距离超过150 km时衰减趋于稳定,在仿真中取α=0.1。
4.1 杂波非平稳补偿分析
图3给出了在近程单元Rs=50 km处,经ETVW法、NL-TVW法、TVW法和3DT法处理后,杂波功率谱的空时分布比较。比较图3(b)~(d)可以发现,尽管3DT法采用减少训练样本数目的方法降低杂波非均匀程度,但由于杂波在近距单元非平稳严重,各单元杂波空时分布激烈变化,直接平均后的杂波谱“变宽”严重;经ETVW、NL-TVW法和TVW法补偿处理后,各距离单元杂波分布基本相同或相近,经平均后的杂波谱明显“变窄”,与最优处理器的杂波分布接近。
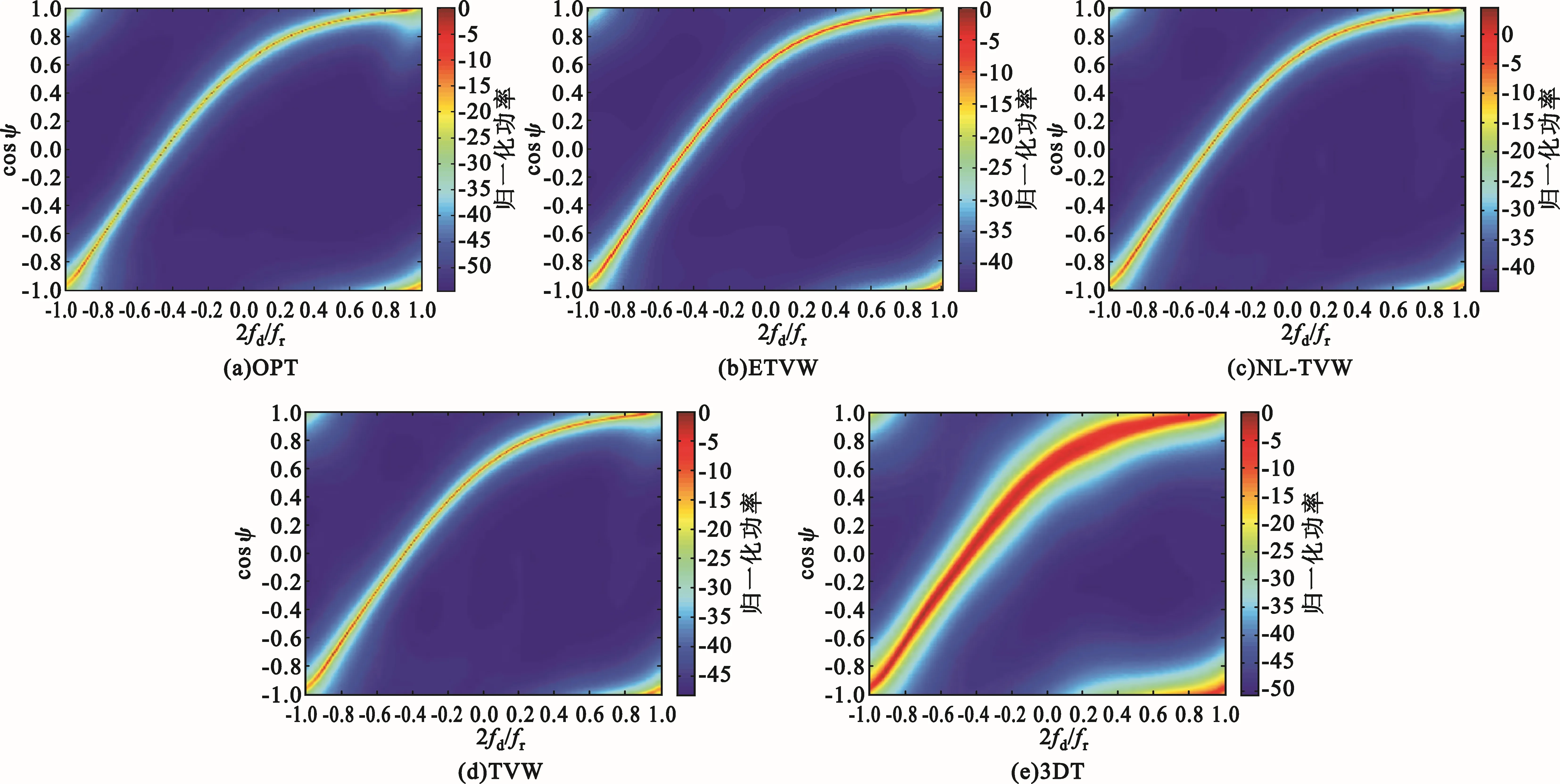
图3 ETVW算法杂波谱比较(Rs=50 km)
4.2 杂波抑制性能分析
图4给出了近程距离单元(Rs=50 km)、中程距离单元(Rs=100 km)和远程距离单元(Rs=150 km)三种条件下ETVW法、NL-TVW法、TVW法和3DT法改善因子的比较。
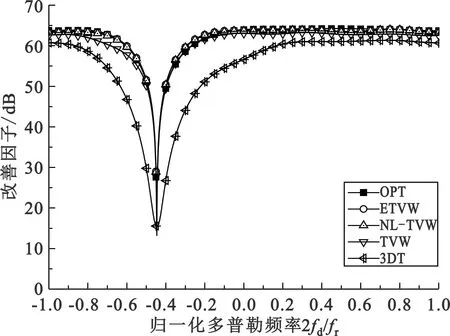
(a)近程距离单元(Rs=50 km)
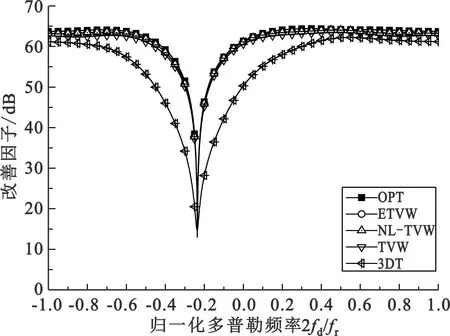
(b)中程距离单元(Rs=100 km)
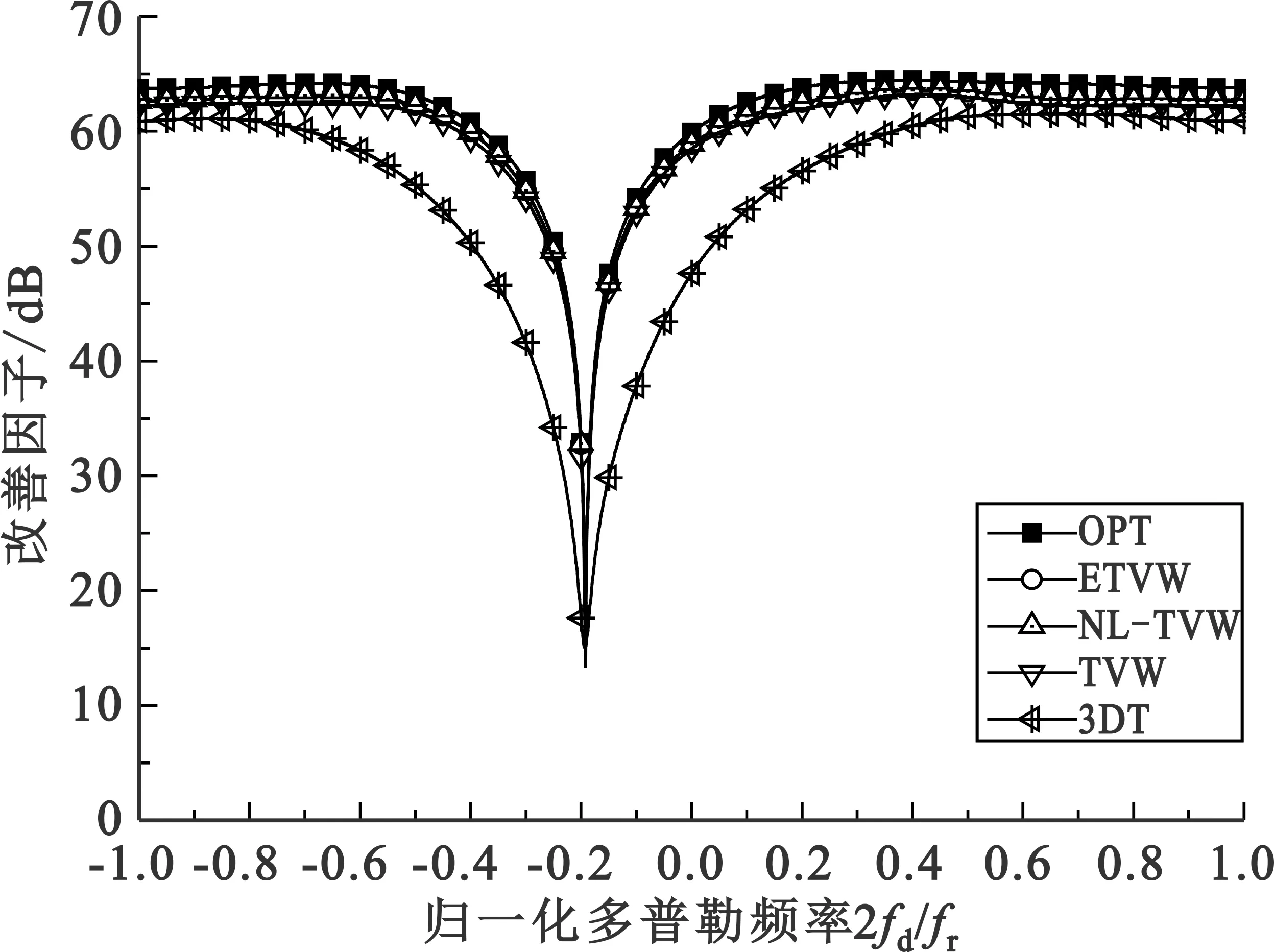
(c)远程距离单元(Rs=150 km)图4 ETVW算法改善因子比较
由于ETVW法采用二阶指数扩展后更加准确地描述了杂波分布的真实特性,经扩展后杂波非均匀特性得到明显改善,由图4可以看出,ETVW法得到的STAP处理器形成“窄而深”杂波抑制凹口,在近、中、远程距离单元,ETVW法的性能均良好,其改善因子比TVW法和3DT法更高,也略高于NL-TVW法。究其原因在于ETVW法在权矢量扩展时,不仅考虑了二次项的影响,而且与NL-TVW相比,通过合理选取衰减系数α,进行补偿时更加符合杂波的分布规律。
进一步对比图4(a)~(c)可以发现,ETVW算法在近程单元的杂波抑制性能比TVW法有明显改善,并且在主瓣区的性能优势更加显著,其改善因子平均优于TVW法约1.39 dB,优于3DT法约7.38 dB,优于NL-TVW法约0.35 dB。而在中、远距离单元,由于杂波趋于平稳,二阶指数扩展和线性扩展的性能相差不大,ETVW法优于TVW法0.77 dB和0.67 dB,和NL-TVW法基本相当。
4.3 运算量分析
ETVW算法中,由于处理器维数扩展到原来的3倍,取N=4和K=8条件下,采用3DT法降维处理后,其训练样本数为72,ETVW法训练样本数目和运算量比较见表2。
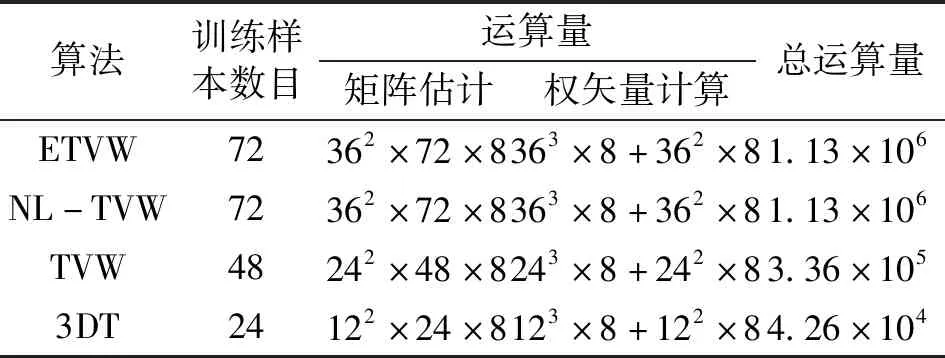
表2 ETVW算法训练样本数目和运算量比较
表2说明,经3DT降维处理后ETVW法运算量约为1.13×106次复乘运算,比全空时处理降低了约90%,约为TVW法的3倍,训练样本数目约为全空时处理的40%,为TVW法的1.5倍,ETVW法与NL-TVW法训练样本数目和运算量完全相同。
5 结 论
本文针对机载双基雷达杂波距离向分布非平稳、STAP技术杂波抑制性能下降问题,提出了一种基于指数形式时变加权算法。理论分析和仿真结果表明,不同距离条件下,该方法均能有效补偿双基的杂波非平稳,在近距场景杂波急剧变化条件下,杂波抑制性能优于TVW法和NL-TVW法,并且无需雷达系统参数和杂波场景的先验知识,具有工程应用前景。

