基于排队论的战术通信混合接入方法*

郭 喆

(1.中国电子科技集团公司第五十研究所，上海 200331;2.中国电子科技集团公司数据链重点实验室，西安 710068)

0 引 言

在军事通信中，战术通信是为了保障战术兵团、部/分队实施战斗指挥而建立的通信网络，包括野战地域通信网、战术电台网、数据链、综合移动通信系统、卫星通信系统等。对于战术无线电通信而言，时延和可靠性是在系统设计时着重考虑的因素，因此传统的战术无线通信采用了静态资源分配技术来管理物理层资源的访问。每个节点都被指定了一个明确的资源配置，具体规定了在什么时候以及怎样使用物理层资源，以避免发生冲突。静态配置的物理层资源的利用率很低，在同一个子网内各节点间存在动态且可能急剧变化的情况下尤其突出。媒体接入层设计的主要目的之一就是解决物理层资源利用率不高的问题，因为扩频通信是战术无线电抗干扰通信的基本手段，多采用时分多址(Time Division Multiple Access，TDMA)技术来调度节点对传输媒介的访问。TDMA能够提供较高的网络容量，并且有助于实现服务质量(Quality of Service，QoS)优先级[1]。

在战术通信领域，TDMA协议的研究对改进报文传输的时延性能具有重要的理论意义和实用价值。文献[2]分别讨论了长短两种报文格式下握手机制，仿真分析了自组织时分多址(Self-Organized TDMA,STDMA)协议在不同业务量及重传参数的时延性能。文献[3]研究了数据链的轮询模型，并且对跨系统之间的时延和系统响应等指标进行了仿真分析。关于提高系统利用率，也有一些关于动态时隙分配算法的文献，例如文献[4]介绍了一种改进的动态时隙分配算法用于武器协同数据链，比较了不同帧长对网络性能的影响；文献[5]将正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)与TDMA结合，提出一种正交时频多址接入(Orthogonal Domain Time Frequency Multiple Access,ODTFMA)协议，研究机群内的子网是否能够采用多个正交频段同时传输；文献[6]研究了入网战术数据链入网广播的软件算法；文献[7]研究了基于动态门限的统计优先级的SPMA(Statistic Priority-based Multiple Access)协议，相比固定门限方法，在信道忙闲比和网络总吞吐量等性能上有较大提升。

以上文献均采用仿真的方法来验证不同的传输模式，但是比较的网络指标各有侧重，其基准并不统一。考虑到时延和网络吞吐量是最基本的网络性能，也是战术通信最为重要的因素，本文采用排队论的方法对TDMA时延情况进行建模分析得到近似的解析模型，然后用仿真的方法验证。此外，提出了基于TDMA和码分多址(Code Division Multiple Access，CDMA)的混合接入方法，使其能够在网络吞吐量不变的前提下大幅提高数据包排队时延性能，并且在保证时延的要求下使网络吞吐量提高近30%。

1 基于排队论的TDMA时延分析

典型TDMA系统的帧结构如图1所示。每个用户独占事先分配好的时隙，与其信令交互放在一个单独的时隙以提高系统效率。其优点是每个时隙对应一个用户，避免了“干扰”和“冲突”。

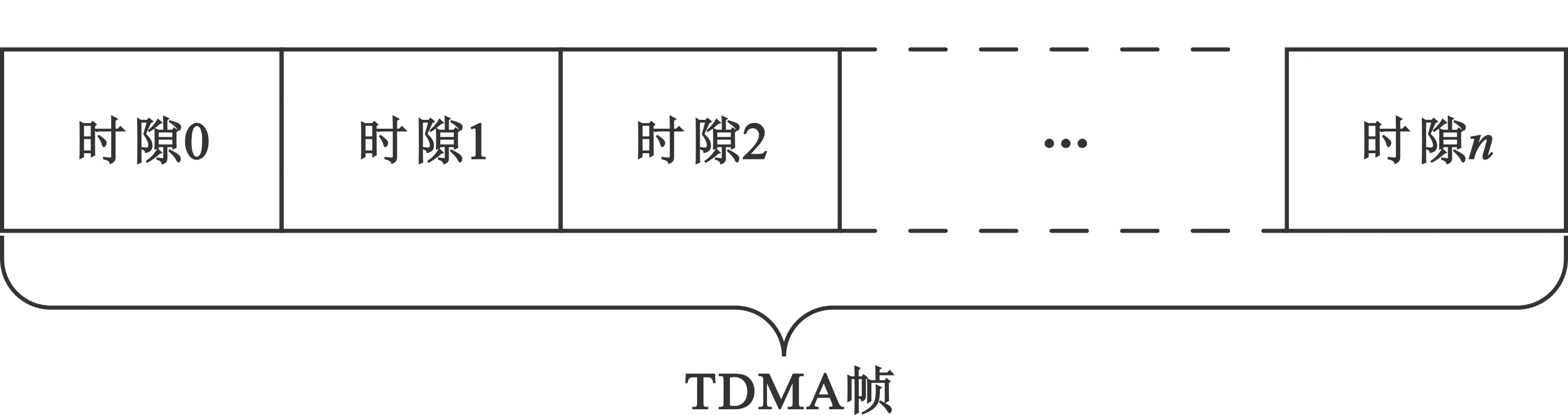
图1 TDMA帧结构

在数据发送过程中，端到端的时延Tdelay由几个部分组成：

Tdelay=t1+t2+t3。

式中：响应时延t1是从报文产生到由物理层发送的时间，受调度算法影响较大；处理时延t2是物理层发送该报文需要的时间，由硬件性能决定；传播时延t3是在空间传输所需的时间，由于电磁波是光速传播，一般在几毫秒内。

在采用固定时隙分配方法的TDMA系统中，每个用户独占一个时隙。假设报文产生模型为泊松流，报文长度为负指数分布，则可以将其看成一个M/M/1队列，即到达速率为λ(报文产生间隔的时间服从平均数为1/λ的负指数分布)，服务速率为μ(报文处理能力为每秒处理μ个报文，即报文长度为1/μ的负指数分布)，队列数为1的排队模型。其响应时延t1相当于排队模型中的等待时间。定义服务强度

(1)

由排队论的知识，

(2)

式中：Ws是逗留时间，即在排队论中顾客达到直到服务结束离开的平均时间。

从式(2)可以看出，在处理能力(μ)一定时，到达速率(λ)越大，时延越大；服务强度(ρ)一定时，处理能力越大，时延越小。这一理论分析结果和常识是相符的。考虑n个时隙，即有n个这样的队列，假设这些队列互相独立，那么在相同的参数λ和μ的情况下，每个队列的平均时延都是一样的。

根据排队论可以理论证明,在服务台数量、服务能力一定时，要使平均等待时间最短，M/M/c模型要优于c个M/M/1模型。即方案1为2个独立无关的M/M/1队列，即有2个队列，每个队列的到达强度为λ/2，服务台的处理强度为μ；方案2为M/M/2队列，即有1个队列，该队列的到达强度为λ，2个服务台，每个服务台的处理强度为μ。方案2的平均等待时间Tq2比方案1平均等待时间Tq1短。传统的TDMA方案中用户与时隙对应关系绑定，可以看成c个M/M/1模型，理论上，将这些用户动态地分配到空闲的时隙上(M/M/c模型)能够缩短时延，因此这里将方案2作为优化对比的参考。

2 混合接入方法

从第1节结论得到启发，如何利用暂时“空闲”的服务台是提升系统性能的关键。但是由于战术通信的特点，为了保证QoS和特定报文的时延，不得不降低部分系统效率。将所有报文按照队列合并的方式进行传输，理论上时延是可以缩短的，但是在多用户接入、关键数据保证和资源保证方面达不到战术要求，在实际操作中不可行。为了平衡两者的需求，本文介绍一种TDMA和CDMA混合的时隙分配方法：将一个业务时隙作为公共时隙，按照CDMA正交码同时给若干的用户使用，但其使用前需要通过信令交互获得PN码，其他时隙与用户对应关系不变。为了不损失网络效能，将报文的产生速率提高到n/(n-1)，其中n为原来业务时隙的数量。业务时隙的分配规则是，每个用户有自己的固定时隙，如果固定时隙上是空闲的，那么新数据报文就在原有固定时隙上发送；如果固定时隙被占用，则通过信令消息申请PN码。如果获得PN码，说明公共时隙资源可用，利用PN码在公共时隙上发送报文；否则需继续等待(排队)，其中PN码的数量可调整。该方法的帧结构如图2所示。

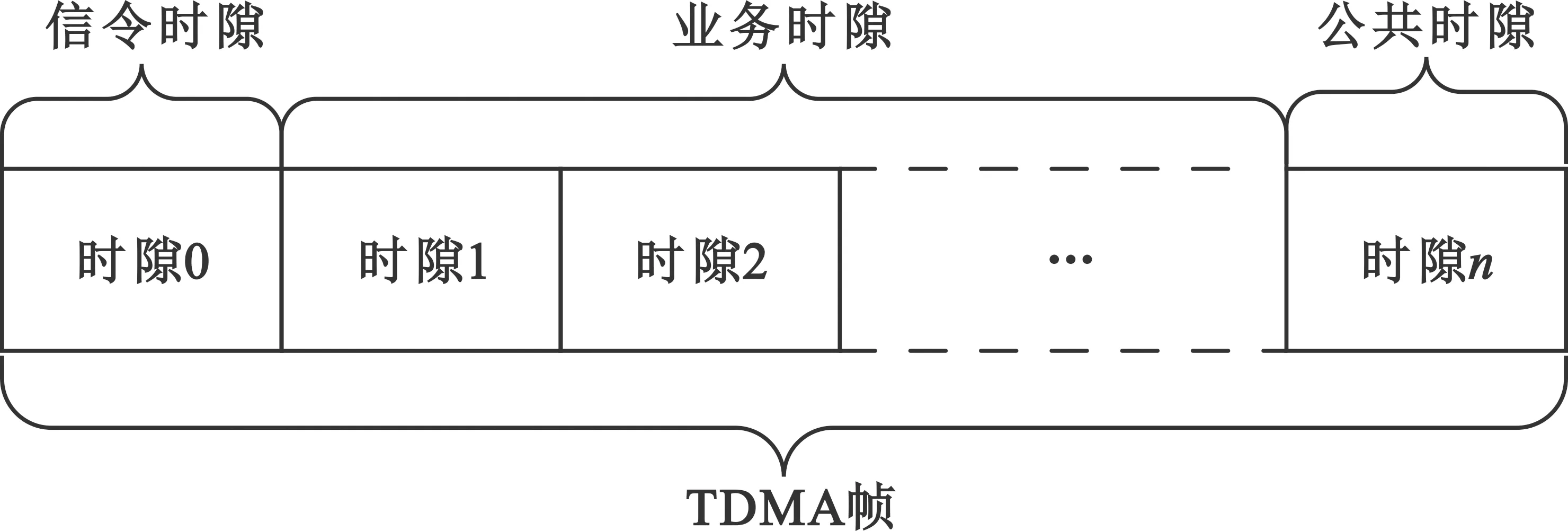
图2 混合接入方法帧结构

在系统组成上，已经调制好的数据会根据系统需求，直接送入TDMA成帧，或先“降速”处理后再与CDMA扩频码发生器调制，然后送入TDMA成帧器成帧。在本文介绍的方法中，CDMA扩频码的码速率并非传统CDMA系统中10倍以上的扩频，而是与已调信息的原始码速率一致。数据在与CDMA扩频码调制之前经过了“降速”处理，因而对CDMA部分而言硬件结构和要求大大简化。可以与TDMA系统的系统时钟和其他通信模块共用，仅比TDMA系统增加扩频码调制/解调环节(由于是低码率扩频，硬件成本较CDMA系统会更低)。核心系统框图如图3所示，算法流程如图4所示。

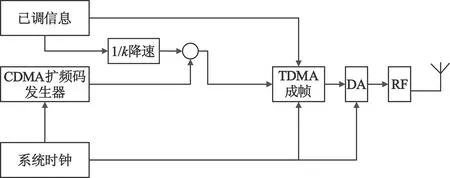
图3 核心系统框图

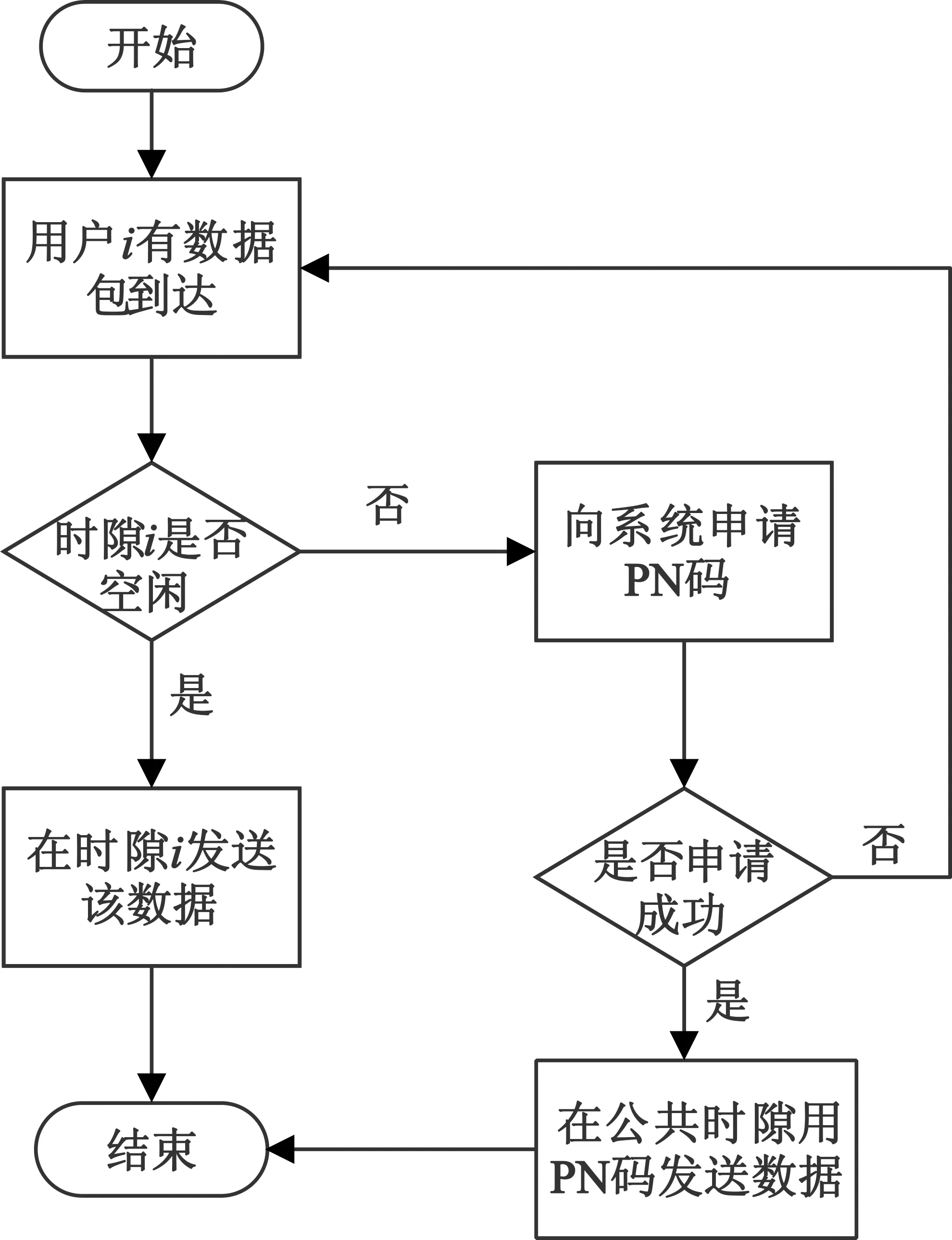
图4 算法流程图

按照本文的混合接入方法，每个用户在公共时隙未被占满的情况下，相当于有2个服务速率不等的队列在服务，其中一个队列是正常服务时间μ,另一个队列是公共时隙的服务时间kμ,其中k是系统划分PN码的个数。

这里给出服务速率不均衡的队列解析结果(队列数n=2)：有两个服务速率不等的队列，队列1的服务速率为μ1，队列2的服务速率为μ2，顾客到达率为λ，ρ=λ/(μ1+μ2)，α=μ2/μ1。当队列都是空闲时，选择队列1的概率为φ。系统空闲的概率

(3)

由此可以求出系统的平均队长

(4)

根据Little公式有

(5)

为了研究这个模型是否符合实际，我们按照8个业务时隙加1个公共时隙做仿真对比，并且取k=2这种情况。其他条件为：λ为400～800个/秒，μ为1 200个/秒。对比情况如图5所示。

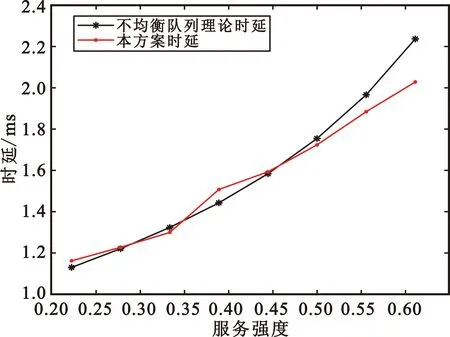
图5 本文方法的近似理论值比较结果

从图5可以看出，本方法的时延与不均衡队列的理论值式(3)和式(4)十分吻合,不同之处在于较低服务强度时延略大于理论值，较高服务强度略小于理论值。原因在于本方案的公共时隙并不是独占的，与两个不均衡服务能力的队列模型稍有差别。造成这种差异可能的原因是，在较低服务强度时，本方法与服务能力不均衡的双队列模型差异不大；较高服务强度时，本方案能够更好地平衡突发流量尖峰，使得平均时延更短。

3 仿真分析

由第1节和第2节的分析可以看出，多队列合一可以缩短时延，划分公共时隙在某种形式上可以看成多队列合一。因此，本文所提方法理论上可以比原有固定时隙更优的时延性能。本节通过仿真分析其具体性能。仿真软件采用Matlab，数据包到达率λ的含义是每秒钟用户产生的数据包个数，服务率μ的含义是系统每时隙每秒能够处理的数据包个数，PN码个数k是指在动态时隙最多同时分配的PN码个数，即同时能够在公共时隙发送数据的用户数。所有仿真都是产生10万个数据包后统计得到。另外，无特别说明的情况下，对时延的仿真比较结果是在网络吞吐量一致的情况下比较的，即在不丢包的情况下，在一个TDMA帧时间内，用本文方法每个用户的发送数据包总数等于原TDMA方法。

首先比较本方案与原TDMA方案的性能提升。由前文所述，当所有时隙都自由分配时(多合一排队方法)，性能最优，因此作为排队性能上限，也同时标注出来当作参考。仿真参数：数据包到达率λ为600～1 100个/秒，服务率μ为1 200个/秒，业务时隙为8，公共时隙为1，PN码数量为2。仿真结果如图6所示。

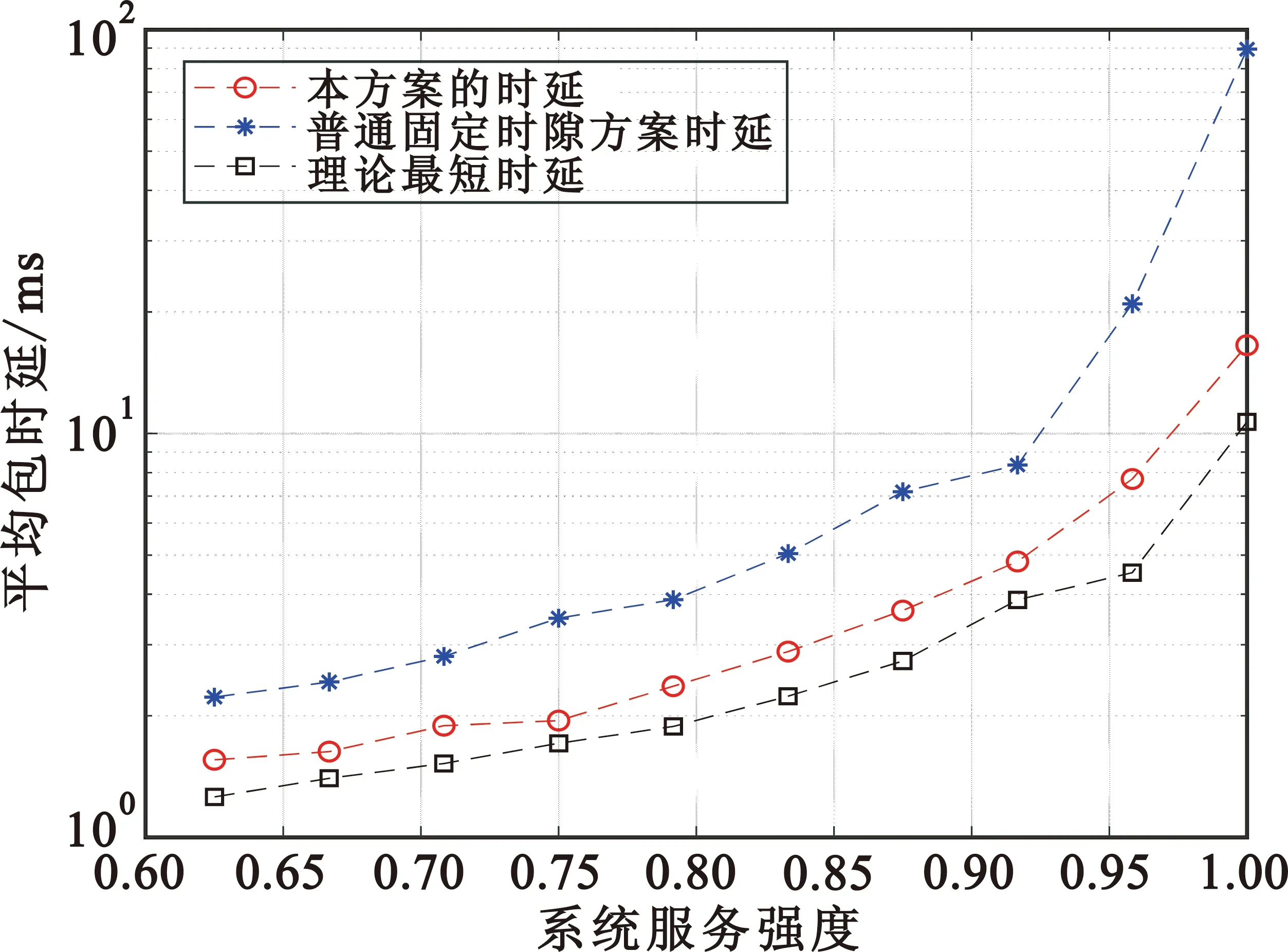
图6 时延性能分析

从图6可以看出，本文方法比原TDMA协议时延性能有大幅提高，在低负载情况下时延为原TDMA协议的70%左右，在高负载情况下时延为TDMA协议的20%,并且与理论最短时延相差不大，且变化趋势相同。

其次，研究在网络吞吐量方面本文方案的性能提升。仿真参数：数据包处理速率为1 200个/秒，数据包的长度服从[400,1 500]字节均匀分布，业务时隙为8，公共时隙为1，PN码个数为2。以实际应用情况考虑，当数据包排队超过100 ms则该数据包溢出丢弃。仿真了不同服务强度下网络吞吐量，结果如图7所示。

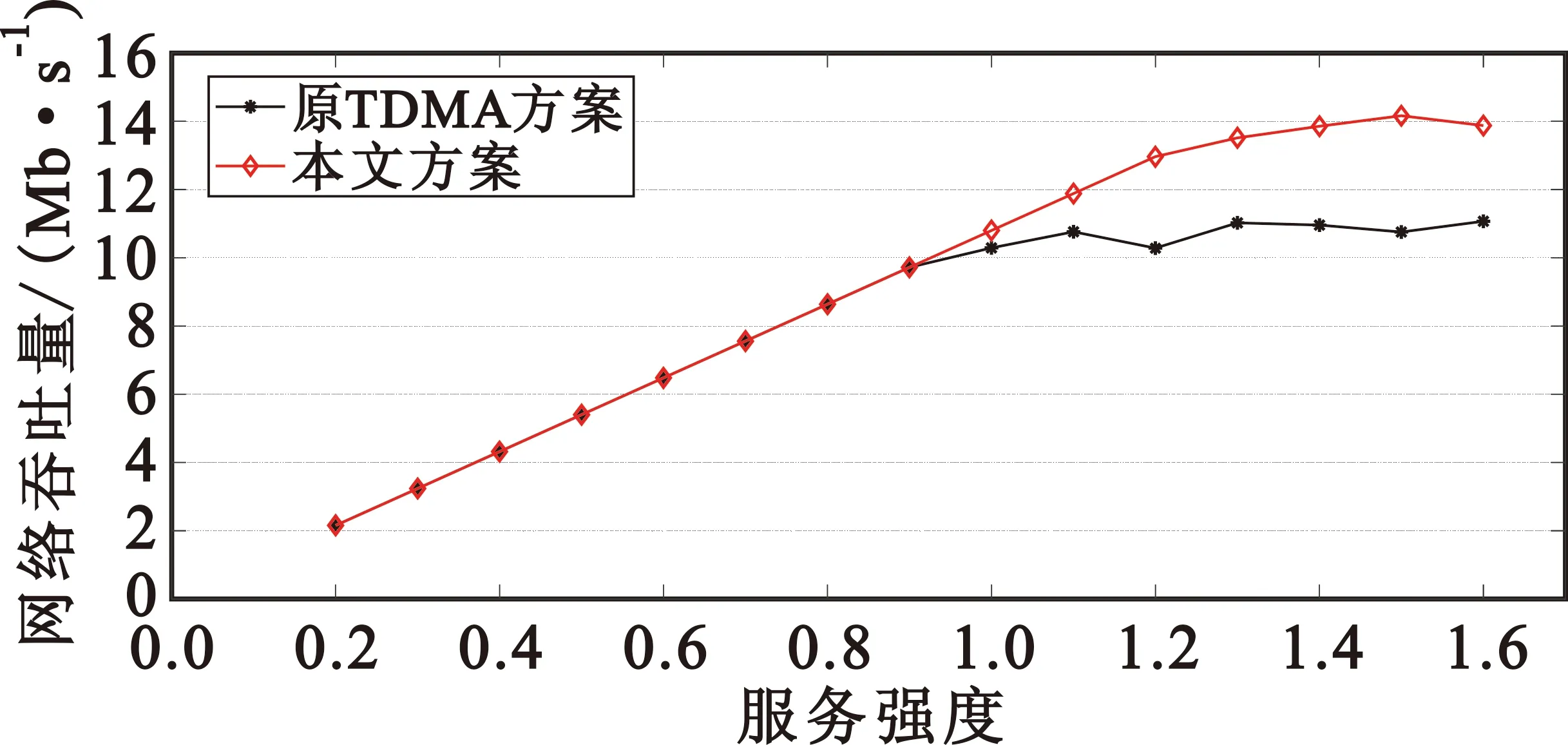
图7 网络吞吐量分析

从图7可以看出，在服务强度小于1时，两种方案都没有发生丢包，网络吞吐量随服务强度线性增长；当服务强度超过1时，原有TDMA方案产生了丢包，但本文方案依然能将数据包发送出去；当服务强度到1.5时，本文方法的网络吞吐量达到最大值，大约比原方案吞吐量有30%的增加。

另一个值得研究的问题就是，PN码的个数k取多少合适。在上述仿真条件下k取1、2、4、8，仿真结果如图8所示。

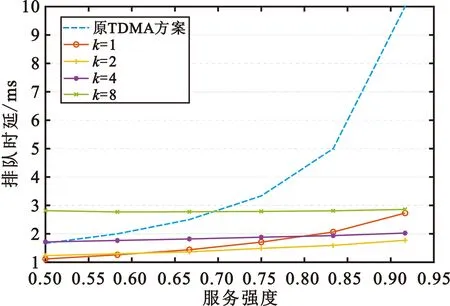
图8 不同k值时延性能分析

从图8可以看出，k=1时在低负载时具有最好性能，k=8时时延性能波动不大。原因是k=8时几乎每个用户在任何时候都有可以接入的资源，但是因为PN码特性，实际速率只有正常速率的1/8，因此低负载时k=8性能并不好，在高负载时k=8能够更好地利用系统能力。在某些特定的应用场景下，例如当网络资源接近耗尽但所有用户均有重要数据发送时，可以采用最大PN码个数的分配方案。为了更好地比较不同k值的性能，我们选择两种负载场景下不同k值的时延性能，不同的k值相当于把公共时隙划分为k个动态的子时隙，仿真结果如图9所示。

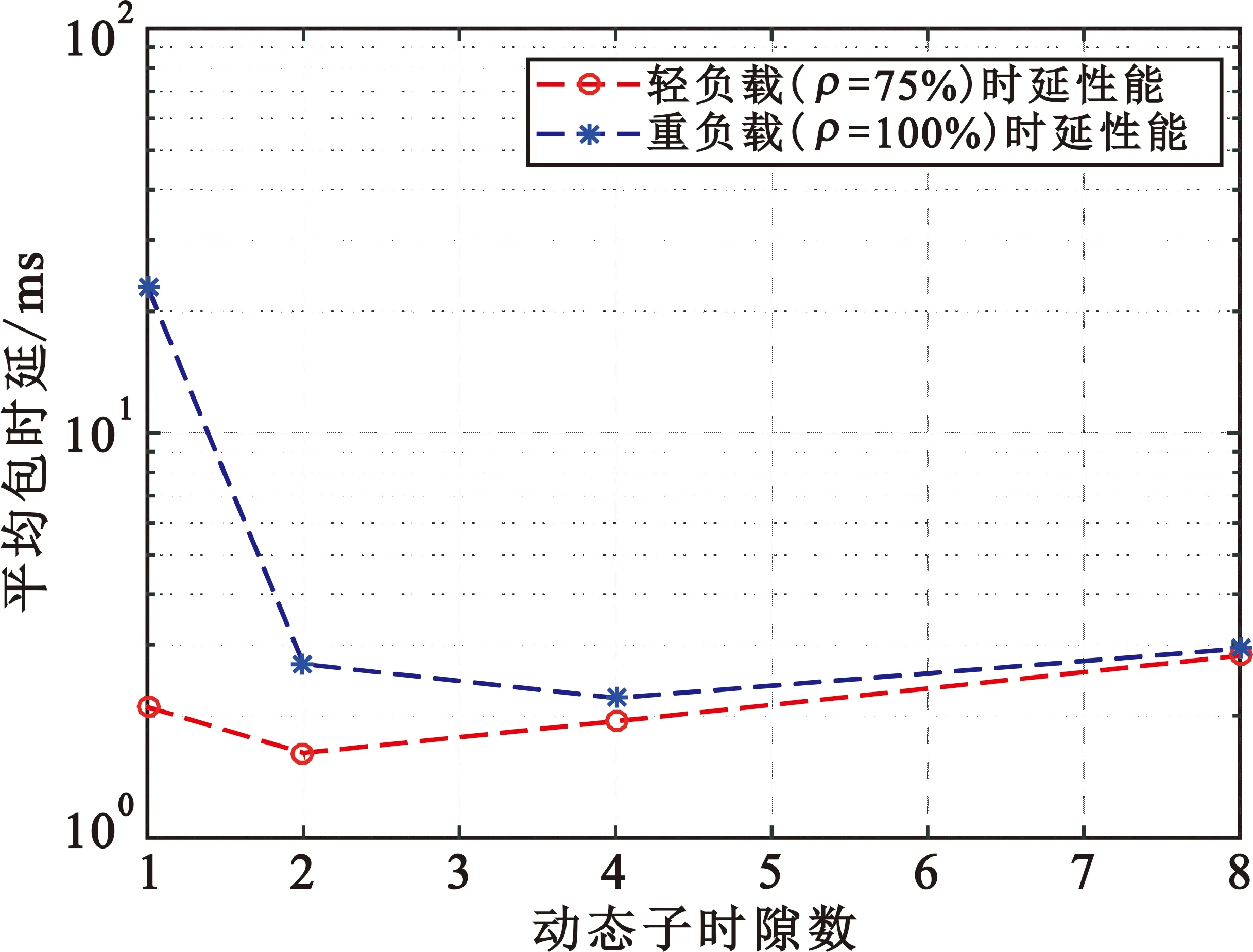
图9 优化k值仿真结果

从图9可以看出，在相同的负载下，k=2或k=4是较优化的结果,即在轻负载场景取k=2，在重负载情况取k=4;在极端情况下，当网络负荷极大，超过设计强度时，可以选择k=8。

本文方案能够有效缩短数据包排队时间，提升网络吞吐量，也会增加有关硬件开销和信令开销，但都十分有限。如前文所述，虽然采用了CDMA在公共时隙来区分不同用户，但因为CDMA的扩频码速率与原用户时隙保持一致，其系统实现难度比一般CDMA系统要简化得多(普通CDMA系统要求码速率10倍以上原数据速率，以达到扩频的目的)，硬件要求也低很多；在信令开销上，增加了申请-回复环节，但由于PN码数量有限，不用回复整个PN码，仅需按照事先编排好的编码回复PN码编号即可(以8个PN码计算，需要3 b的编码)，信令负荷也不大。因此其系统实现复杂度的轻微增加是可接受的。

4 结束语

本文提出一种TDMA和CDMA混合接入的时隙分配方法，利用排队论分析了所提方法在时延上的优越性能，仿真结果也较好地印证了理论分析结果，兼顾了TDMA资源保障特性和系统效率。本文所提出方法与不均衡队列模型很好拟合，并和M/M/c模型有相同的变化趋势，在高负载条件下性能更加突出。此外，对于PN码的个数优化，在低负载时k值取2较好，在高负载时k值取4较好。后续工作有：加入对优先级的考虑；考虑实际信道传输情况，加入丢包率因素；研究不同业务时隙条件下优化k值问题。