气动盘对气动杆模型减阻效率的影响

范 冰，黄 杰，单先阳

(1.南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016) (2.南京航空航天大学飞行器先进设计技术国防重点学科实验室，江苏 南京 210016) (3.湖北航天技术研究院总体设计所，湖北 武汉 430040)

随着航空航天技术的发展，为满足军用和民用需求，飞行器飞行马赫数越来越高，其中高超声速飞行器是近年来研究的热点课题。高超声速飞行器在飞行过程中会产生巨大的激波阻力[1-2]，这会严重影响飞行器的气动性能，因此研究高超声速减阻技术对提高飞行器的性能具有重要的工程意义。

近些年国内外研究较多的一种高超声速减阻技术是在飞行器头锥处安装气动杆。气动杆可降低激波强度，从而达到减阻的目的。从20世纪50年代起就开始了与气动杆减阻相关的试验和数值研究[3-5]，并且已经实现了高超声速飞行器的工程化应用，如美国的三叉戟Ⅱ型弹道导弹。气动杆能将高超声速飞行器头锥前方的弓形激波推离物面，其核心技术是将强激波转化为斜激波，从而减弱激波强度，达到降低飞行器气动阻力的目的。Dem'yanov、Kalimuth、Qin等[6-8]通过数值方法研究了气动杆的减阻性能，结果表明增加气动杆长度和直径能提高系统的减阻效率，此外在气动杆前端安装气动盘也能提高减阻效率。

本文采用数值方法研究气动盘对减阻效率的影响，对比无气动盘和有气动盘模型的阻力系数，并在此基础上研究了气动盘形状对减阻效率的影响，给出了气动盘设计方案。

1 物理与数值模型

本文主要研究在高超声速来流条件下气动盘对气动杆模型减阻效率的影响，物理模型如图1所示。其由三部分构成，分别为钝头体、气动杆和气动盘。其中钝头体为半球体，直径D为100 mm，用于模拟高超声速飞行器。气动杆安装于钝头体前端，其长度L和直径D2分别为100 mm和2 mm。尖锥形气动盘安装于气动杆的前端，其直径D1为16 mm，前半锥角β1和后半锥角β2分别为30°和50°。此外为了分析气动盘的减阻效率，本文同时建立了3种分析模型，如图2所示，前两种分别为不带气动盘的尖杆和钝杆模型，第三种为带尖锥形气动盘的模型。

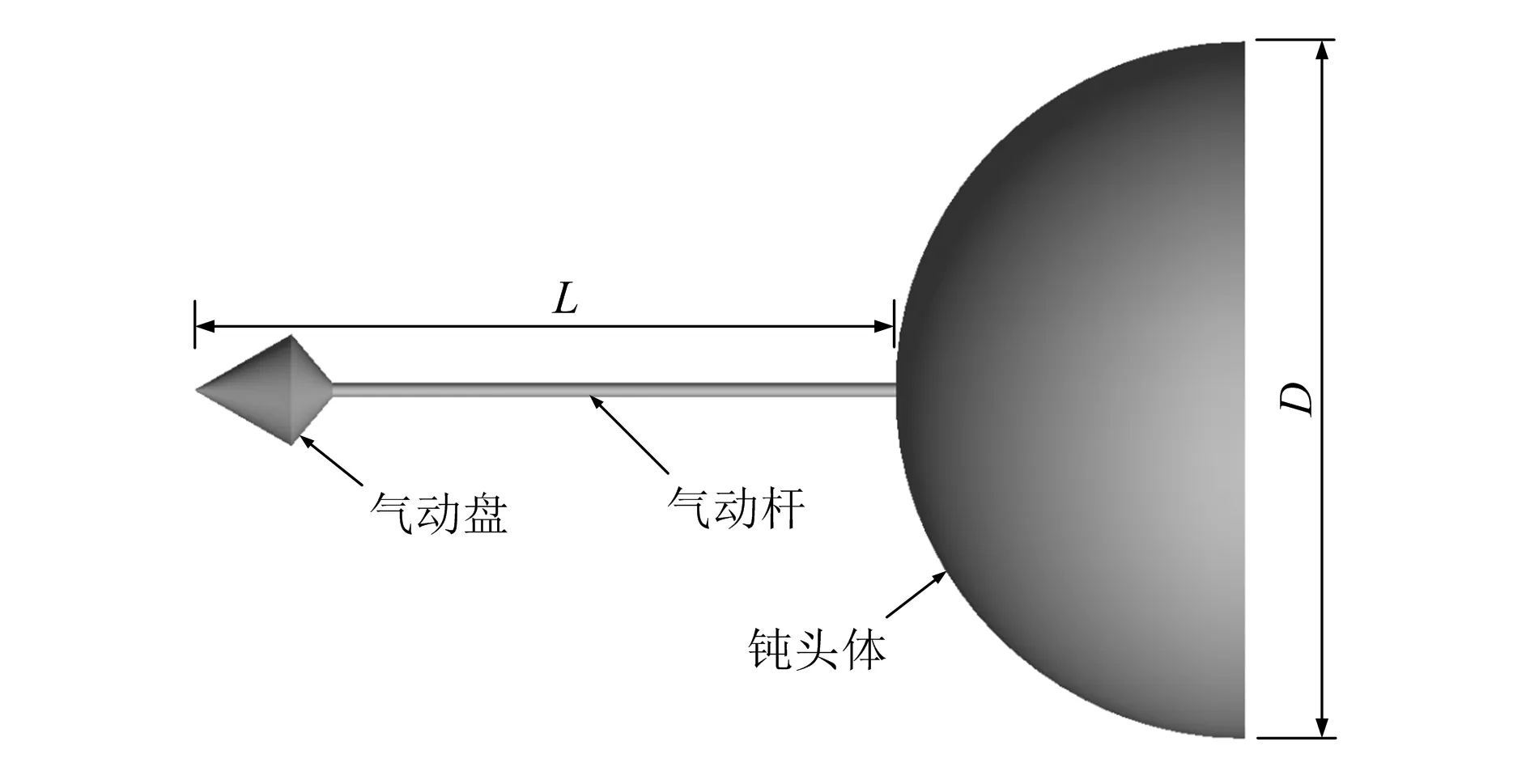
图1 物理模型

本文数值计算采用的高超声速自由来流马赫数Ma∞、来流静压P∞、来流静温T∞及来流攻角α见表1。根据几何模型和来流条件，采用ANSYS ICEM CFD软件划分了轴对称的CFD结构网格，如图3所示。CFD数值模型的边界条件包括远场边界、对称轴及无滑移壁面(钝头体、气动杆及气动盘)。本文通过CFD数值方法求解雷诺平均Navier-Stokes方程获得分析模型的壁面压强和气动阻力，并采用二阶精度的AUSM+空间离散格式[9-10]、Menter's SSTk-ω湍流模型[11]及LU-SGS时间推进格式[12]。CFL数在求解初始阶段设置为0.5，随着求解的进行逐渐增加至5.0，且在求解过程中监控分析模型的阻力系数，以容差1×10-5作为其收敛标准。

图2 不同气动杆模型

表1 自由来流参数

图3 计算网格

2 结果与讨论

2.1 流场结构

本文采用CFD数值方法进行了尖杆、钝杆和带尖锥形气动盘模型的高超声速气动阻力分析，流场马赫云图和流场结构如图4所示。由图4(a)可知，高超声速来流受到尖杆的压缩从而产生了一道斜激波。在钝头体前方由于流动分离形成了一个回流区，回流区的外缘为剪切层。此外在钝头体中部形成了一道再附激波，再附激波的强度决定了钝头体压强峰值及其位置。由图4(b)可知，钝杆模型的流场结构和马赫云图与尖杆模型基本相同，唯一区别为钝杆前方产生的是弓形激波。由图4(c)可知，尖锥形气动盘对高超声速来流扰动明显大于尖杆和钝杆，钝头体前方的旋涡区也明显增大，这将迫使激波再附点后移，导致钝头体压强峰值的位置向下游移动。最为核心的是带尖锥形气动盘模型的再附激波强度明显弱于尖杆和钝杆模型，这将降低钝头体的压强峰值，对降低高超声速钝头体的气动阻力是有利的。因此从流场结构和再附激波强度的角度可以定性判断带尖锥形气动盘的模型具有更好的减阻效率。

图4 不同分析模型的流场马赫云图和流场结构

2.2 减阻效率

图5给出了尖杆、钝杆和带尖锥形气动盘模型的钝头体压强分布。结果表明尖杆和钝杆模型的钝头体压强分布相差很小，钝杆模型的压强峰值略低于尖杆模型。带尖锥形气动盘模型的钝头体压强分布在0°～45°区域内明显低于尖杆和钝杆模型，在45°～80°区域内略高于另外两种模型，而在80°～90°区域内3种模型的钝头体压强分布相差很小。带尖锥形气动盘模型的压强峰值比尖杆和钝杆模型分别降低了35.74%和35.37%。此外带尖锥形气动盘模型的压强峰值明显位于尖杆和钝杆模型之后，这是由于安装气动盘后钝头体前方回流区增大，激波再附点向后移动造成的。

图5 不同分析模型的钝头体壁面压强分布

表2列出了3种分析模型的阻力系数，其中阻力系数Cd的计算公式为：

(1)

式中：F为阻力；ρ∞为来流密度；V∞为来流速率；S为参考面积，定义为钝头体的投影面积πD2/4。结果表明钝杆模型的阻力系数仅仅比尖杆降低了0.50%，而带尖锥形气动盘模型的阻力系数比尖杆和钝杆模型分别降低了24.32%和23.95%。因此在气动杆前端安装气动盘可有效降低高超声速气动阻力，提高飞行器的性能。

表2 不同分析模型的阻力系数

2.3 气动盘形状的影响

以上分析结果验证了带尖锥形气动盘模型的优异减阻性能，在此基础上本文研究了气动盘形状对减阻效率的影响。除尖锥形气动盘外，本文研究了另外3种形状的气动盘的减阻效率，如图6所示，分别为半球形气动盘、平面盘1和平面盘2。所有气动盘的直径D1和后半锥角β2均相同，且平面盘2的厚度t为2 mm。

图6 不同的气动盘形状

图7给出了半球形气动盘、平面盘1和平面盘2的流场马赫云图。结合图7和图4(c)可知，平面盘1和2的再附激波强度在4种形状的气动盘中是较弱的，因此可以定性判断安装平面盘能够获得最小的钝头体压强峰值，这对减阻是有利的。图8给出了在4种形状的气动盘下计算获得的钝头体壁面压强分布。结果表明半球形气动盘模型的钝头体壁面压强分布低于尖锥形气动盘模型，平面盘2的钝头体壁面压强分布在4种模型中最低。此外平面盘2的钝头体壁面压强分布与平面盘1相差很小，因此在平面盘1前端安装圆柱形平台对降低钝头体壁面压强的效果不明显。表3给出了在4种气动盘形状下计算获得的阻力系数。结果表明平面盘2的阻力系数比尖锥形气动盘、半球形气动盘及平面盘1分别降低了19.69%、12.73%和0.61%，因此平面盘2具有更好的减阻效率。平面盘具有优异减阻性能的根本原因是其当量半径比其他形状的气动盘都大，因此其对原始激波的扰动及削弱也最大。此外平面盘还具有易加工制造的优点。

图7 不同气动盘形状下的流场马赫云图

表3 气动盘形状对阻力系数的影响

图8 不同气动盘形状下的钝头体壁面压强分布

3 结论

1) 安装气动盘能有效降低再附激波强度，提高气动杆的减阻效率。安装气动盘时钝头体前方的回流区也比无气动盘时大，这迫使激波再附点及钝头体压强峰值向后移动；

2)平面盘具有优异的减阻性能，且其还具有易加工制造的优点，推荐在工程中使用。