基于遗传算法的冲压自动送料装置悬臂梁的优化设计

胡继涛，汪永明，谈莉斌，董书豪

(安徽工业大学机械工程学院，安徽 马鞍山 243032)

目前，自动送料装置在单机多工位冲压系统中应用十分广泛。为了保证自动送料装置在特定工况下能够获得更高的稳定性和经济效益，需要对其结构参数开展优化设计研究。选用的优化方法是否合适，会严重影响最终优化设计的结果。就数值优化方法而言，梯度法、约束变尺度法、序列二次规划法等传统算法的优化效率较高[1-3]，但最终结果往往是局部最优的，很难保证能得到全局最优解。相比较而言，粒子群算法、蚁群算法、遗传算法等寻优方法的全局性较好，其中遗传算法是一种仿生优化算法，能够只利用目标函数值的信息作为搜索信息，在种群中进行大规模寻优，有着其他算法无法比拟的优越性[4-6]。

由于单机多工位冲压系统中工位间的可操作空间十分有限，且大部分悬臂梁较长，因此合理的材料选择和截面尺寸设计显得尤为重要。在满足实际工况约束的情况下，本文选用遗传算法对自动送料装置的悬臂梁抓取结构进行优化设计，以保证最终优化结果为全局最优。在对悬臂梁截面尺寸进行优化设计时，以悬臂梁质量最轻为目标进行优化求解。

1 自动送料装置及悬臂梁结构设计

某销合链链板单机多工位冲压系统主要由冲床、冲床上下模座、冲床上下模、储料装置以及自动送料装置等5部分组成。冲床的一次冲压，可以完成销合链链板的3道工序：一折、成型和冲孔。工位间工件的运输利用自动送料装置完成，主要包括竖直和水平两个方向上的运动，竖直方向上借助无杆气缸完成上下往复运动，水平方向上借助线性模组完成左右往复运动，如图1所示。

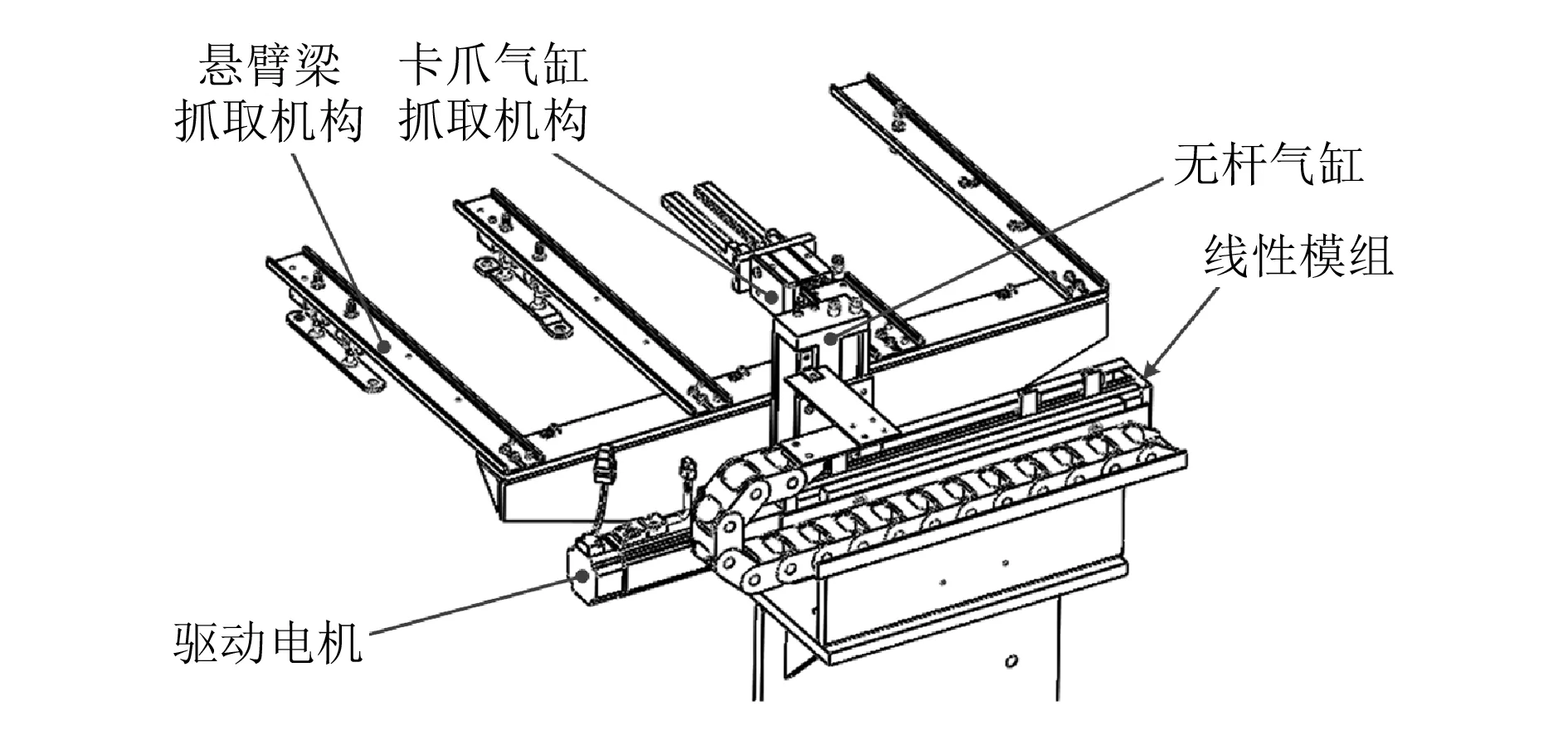
图1 自动送料装置

图1中，工件的抓取方式有2种：1)借助真空吸盘完成工件的吸取和放置；2)借助气动平行型卡爪完成工件的抓取和放置。整个抓取和放置机构主要借助悬臂梁来完成，由此可见，悬臂梁的选材和结构设计对自动送料装置的稳定性尤为重要。由于工位间运动空间十分有限，且要保证悬臂梁的弯曲强度，设计时初选U型截面的悬臂梁。悬臂梁抓取结构主要由U型悬臂梁、真空吸盘及其支架和传感器及其支架组成，如图2所示。悬臂梁的长度L=0.5 m，单个吸盘及其支架质量m1=0.03 kg，传感器及其支架质量m2=0.05 kg，工件质量m3=0.2 kg。为了满足高效的冲压作业要求，需要对送料装置的悬臂梁结构进行优化设计。

图2 悬臂梁抓取结构设计

2 悬臂梁优化设计模型

2.1 截面参数说明

由于实际工况的要求和限制，悬臂梁的长度是一定的，可以进行优化的就是悬臂梁U型截面尺寸，如图3所示。其中悬臂梁的宽度B、高度H和厚度d是主要变量，单位为m。为了后续计算过程的方便，又引入部分辅助变量h,e1,e2和b。s为截面重心，x为截面重心所在的x轴。

图3 悬臂梁U型截面及其参数

2.2 优化目标函数

目标函数是设计过程中预期所要达到的目标与各有关设计变量之间的函数表达式。根据悬臂梁的截面参数，取设计变量为：

X=[x1,x2,x3]=[B,H,d]

(1)

根据悬臂梁的结构设计要求，优化目标为在满足相关要求的情况下使U型悬臂梁的质量最小，即目标函数为：

minf(x1,x2,x3)=ρ×[x1x2-(x2-x3)(x1-2x3)]×L

(2)

式中：f(·)为悬臂梁的质量，kg；ρ为悬臂梁材料的密度，kg/m3。

2.3 约束条件

1)性能约束函数。根据本文悬臂梁抓取结构的设计要求，结合材料力学计算公式，得出悬臂梁最大挠度fv的约束条件为：

(3)

其中：

P=2m1+m2+m3

(4)

(5)

(6)

e2=H-e1

(7)

式中：P为单个悬臂梁抓取结构(除U型悬臂梁外)抓取工件后的质量，kg；b为U型悬臂梁内侧宽度；E为材料的弹性模量；[f]为实际工况所允许的最大位移，取5×10-3m；Ix为U型悬臂梁截面对x轴的惯性矩；h为重心到U型悬臂梁地面的高度，m；e1和e2为重心到相应边的距离，m；g为重力加速度，取10 m/s2。

2)边界约束函数。由于实际工况及工位间的空间限制，为了避免与模具发生干涉，需对悬臂梁的截面尺寸进行限制，如式(8)所示，单位为m。

(8)

根据实际调研情况和工况的限制,以悬臂梁材料分别为45钢、轧制青铜、硬铝合金和PVC板4种典型的常用材料为例进行分析，材料参数见表1。

表1 4种材料相关参数

2.4 建立优化数学模型

根据上述目标函数和约束条件及相关数据，得出悬臂梁质量最优化数学模型如式(9)所示。

(9)

3 悬臂梁优化设计模型的遗传算法求解

3.1 优化过程及结果

为了满足轻量化设计的要求，分别选用表1中的4种不同材料，采用遗传算法对单个悬臂梁的截面尺寸进行目标优化。优化算法的控制参数设置为：种群规模NP=20，迁移概率F=0.5，交叉概率CF=0.8，适应度函数值偏差默认为1×10-6，遗传迭代次数T=100，其余保持默认设置。根据遗传算法优化的流程，通过MATLAB的编程计算，分别得出45钢、轧制青铜和硬铝合金的最优解，如图4～图6所示。

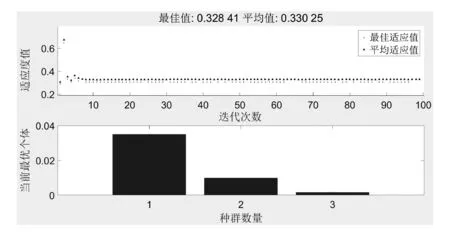
图4 45钢的遗传算法优化结果

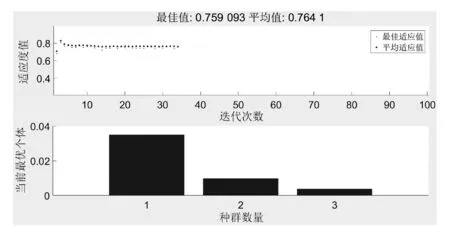
图5 轧制青铜的遗传算法优化结果

由图可知，当材料为45钢时，大约从40代开始目标值的波动很小，所形成的曲线接近水平线，即随着种群代数的不断增加,最优个体的适应度函数值不断减小并逐渐收敛趋于稳定,可确定x1=0.035 m，x2=0.010 m，x3=0.002 m，目标函数值f(x)≈0.327 kg,已经十分接近最优解；当材料为轧制青铜时，最优解为x1=0.035 m，x2=0.010 m，x3=0.004 m，目标函数值f(x)≈0.763 kg；当材料为硬铝合金时，最优解为x1=0.035 m，x2=0.010 m，x3=0.003 m，目标函数值f(x)≈0.196 kg；当材料为PVC板时，迭代无法进行，得不到收敛的运算结果，即在约束条件的制约下，PVC板无法满足要求。

图6 硬铝合金的遗传算法优化结果

3.2 对比分析

45钢、轧制青铜、硬铝合金和PVC板4种材料的最终优化结果对比见表2所示，不难看出，在非线性约束条件的制约下，不同材料的最优解有所不同。在满足弯曲变形的条件下，悬臂梁材料为轧制青铜时其质量最大，达到0.763 kg；为硬铝合金时其质量最轻，即0.196 kg。PVC板无法满足工况的工作要求。由表2的对比结果可知，当悬臂梁的材料选择硬铝合金时，自动送料装置的质量最轻。

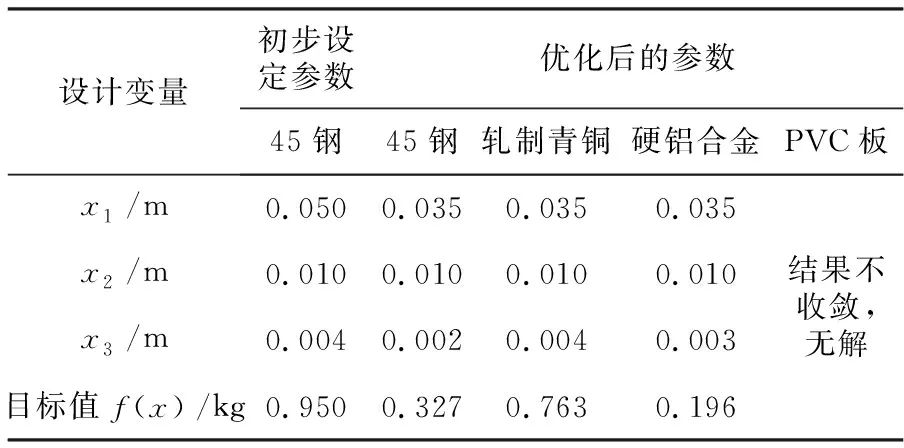
表2 优化前后对比

4 校核验证

为了验证硬铝合金悬臂梁是否满足工况要求，基于ANSYS对单个悬臂梁抓取结构进行校核，得到优化后悬臂梁的位移云图和等效应力云图分别如图7和图8所示。由图可以看出，悬臂梁最大位移约为0.001 5 m，远远小于0.005 m的挠度要求；其受到的最大应力为10.1 MPa，远远小于硬铝合金的屈服极限195 MPa。可见，当悬臂梁材料为硬铝合金时，在满足屈服强度和挠度要求的同时，实现了悬臂梁轻量化的设计要求。

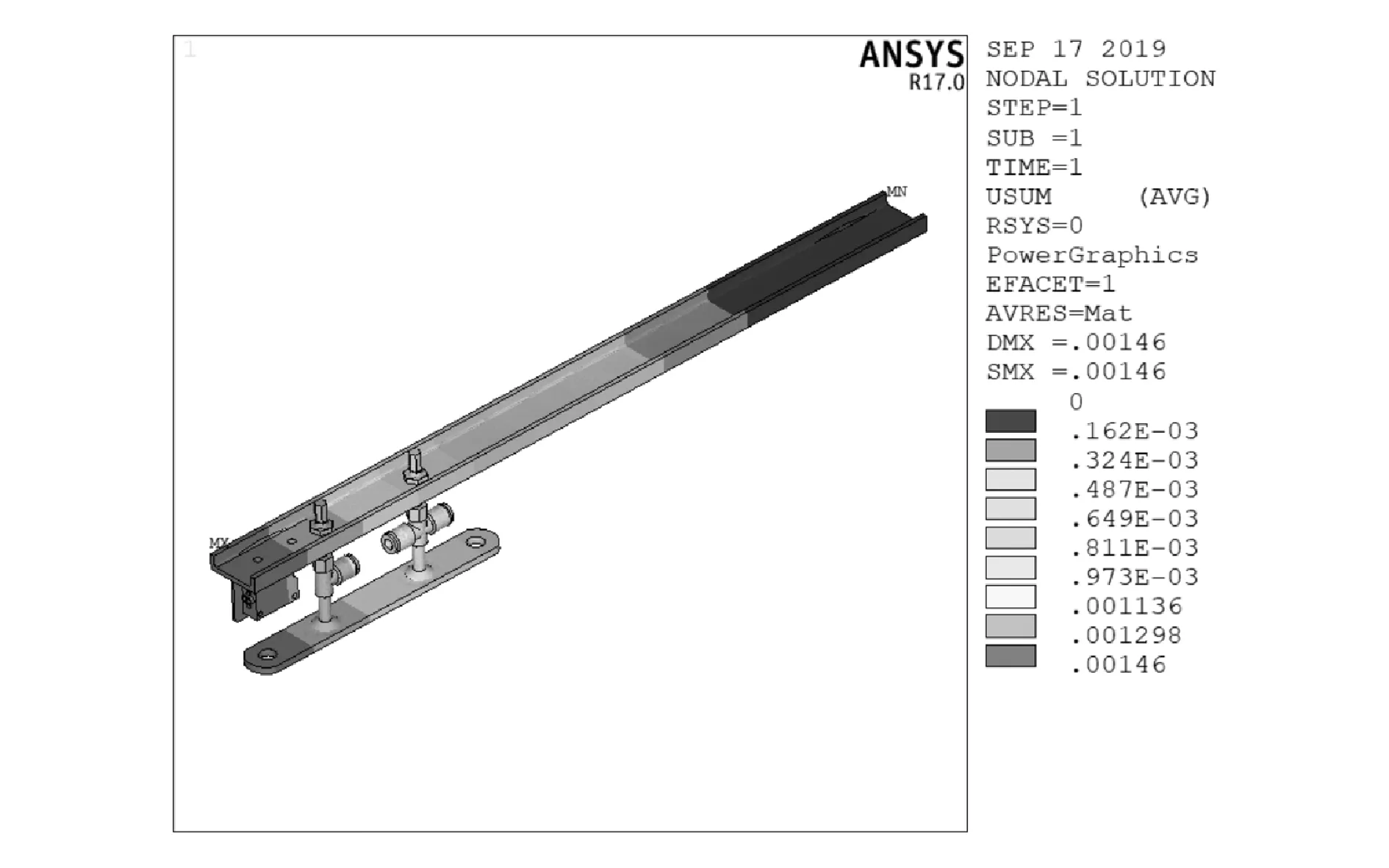
图7 悬臂梁优化后的位移云图

图8 悬臂梁优化后的等效应力云图

5 结束语

针对单机多工位冲压系统自动送料装置悬臂梁的结构轻量化设计需求，本文以U型悬臂梁的质量最小为优化目标，悬臂梁的挠度要求和结构尺寸限制为约束条件，基于MATLAB的遗传算法对自动送料装置的U型悬臂梁的截面尺寸参数进行了优化设计。借助ANSYS分析软件，对截面尺寸优化后的硬铝合金U型悬臂梁进行了性能校核验证，结果表明优化后的U型悬臂梁满足自动送料工况下的屈服强度和挠度要求。本文提出的U型悬臂梁结构优化模型和分析方法，为后续更为复杂工况的结构优化设计提供了有益的参考。