分组随机化隐私保护频繁模式挖掘*

郭宇红,童云海,苏燕青

1(国际关系学院 网络空间安全学院,北京 100091)

2(北京大学 智能科学系,北京 100871)

频繁模式挖掘应用广泛,比如:医学研究人员希望通过分析医学普查数据,发现疾病间的关联,获取并发症等病学知识[1]——例如患糖尿病的人通常伴随着冠心病和高血压.然而在数据普查时,出于隐私的考虑,许多人在提供个人数据时会感到不安,有时拒绝提供数据或提供假数据.如何在保护好个人数据隐私的同时实施频繁模式、关联规则等挖掘任务,是隐私保护数据挖掘(privacy preserving in data mining,简称PPDM)[2]要解决的重要问题,其目标是在不精确访问个体隐私数据的情况下,仍能挖掘到精确的结果.

(1) 相关工作

随机化回答RR(randomized response)最先由Warner 在1965 年针对二元敏感性问题调查提出[3],称为沃纳模型.文献[4]提出了分层沃纳模型,但分层沃纳模型解决的仍是单属性敏感问题的调查,且敏感属性是二元变量.文献[5]使用“风险-效用”映射(risk-utility,简称R-U)比较了不同的随机化策略,提出了用于单一布尔属性的最优随机化策略.文献[6]利用多目标优化方法,针对单一多元分类属性,力图寻找接近于最优随机化的变换概率矩阵.文献[7]提出了针对多个敏感属性的随机化回答技术.文献[8]通过不相关问题随机化回答技术估算多个混合类型敏感属性的依赖关系,其中,混合类型敏感属性包括你是否抽烟、是否有经济负担等二元分类属性,还包括睡眠质量、手机对学业的影响度等量化数值属性.Du 等人基于随机化回答技术实现了布尔类型数据的隐私保护决策树分类[9].不同文献的区别包括属性类型(二元、多元、量化数值)、属性数量(单属性、多属性)、目标(简单统计、相关性分析、决策树)、随机化问题(正/反问题、正/不相关问题)等.

随机化回答是隐私保护频繁模式和隐私保护关联规则挖掘中的主要方法[10-14].文献[10]提出了基于随机化回答的隐私保护关联规则挖掘方法mask(mining associations with secrecy konstraints),mask 随机化过程只有一个参数p,其基本思想是:对布尔数据中所有的“1”“0”值,以p的概率保持不变,以1-p的概率取反.文献[11]针对数据中“1”“0”敏感度不同的问题提出了emask 算法,该算法对“1”“0”设置两个不同的随机化参数p1和p2,emask 随机化时,对所有的“1”值,以p1的概率保持不变,以1-p1的概率取反;而对“0”值,则以p2的概率保持不变,以1-p2的概率取反.从而使“1”“0”拥有不同的保护级别.文献[12]对mask 支持度重构进行了性能优化,提出了mmask 算法.文献[13,14]针对不同属性需要不同保护的场景,提出了“非统一”参数的隐私保护关联规则RE (recursive estimation)算法.文献[15]提出了属性分组的随机化方法,实现隐私保护关联规则挖掘.近些年流行的差分隐私保护[16-18]通过在数据分析过程或结果中添加随机噪音,确保在数据库中插入或删除任意一条记录都不会显著影响数据分析结果,随机化回答是差分隐私的一种变体[17].

(2) 本文动机

本文动机来自于两方面:一是文献[13],二是客观存在的不同人群隐私保护需求的差异性.

文献[13]RE 算法认为:“性别”“年龄”和“收入”等不同属性的敏感度是不同的,应设置不同的随机化参数,使其拥有不同的隐私保护度.既然不同属性都需要不同保护,那不同个体是否需要不同保护呢?

AT&T 实验室1999 年调查了Internet 用户对隐私保护的态度,结果显示[1]:17%的用户对隐私保护极端重视,56%的用户对隐私保护中度重视,其余27%的用户对隐私保护不重视.以上事实说明,不同人群对隐私态度和对隐私信息的保护需求是有差异的.然而,已有的隐私保护频繁模式挖掘方法没有考虑不同人群的隐私保护需求差异性,在对个体数据随机化时,运用统一的随机化参数对所有人实施同等的保护,无法满足个体对隐私的偏好和具体保护需求,造成的结果是对一部分人的隐私保护程度不足,而对另一部分人实施了过度保护.个性化隐私保护[18-21]应运而生.文献[18]提出一种个性化的差分隐私保护系统.文献[19]面向个性化的隐私保护数据发布.文献[20]提出一种精细化的个性化隐私保护框架.文献[21]提出一种个性化的隐私保护问题调查统计方法,与本文工作相似,它允许用户抽取自己的概率对答案进行干扰.然而,文献[21]的问题和应用场景与本文不同,文献[21]针对在线问题调查,而非频繁项集挖掘.

基于以上事实,本文在我们提出的PN/g模型[22]的基础上,提出一种基于个体分组多参随机化的隐私保护频繁模式挖掘方法GR-PPFM(grouping-based randomization for privacy preserving frequent pattern mining).在GR-PPFM 架构中,当人们参与数据调查提交自己的数据时,可以根据各自偏好进行分组,每一组数据设置不同的隐私保护级别,进行差异化的隐私保护.本文是我们在文献[22]工作的延续.文献[22]针对PN/g模型,总人数为N,组数为g,每一分组的人数相同,均为N/g.文献[22]通过简单的例子,手工计算探索了支持度重构的可行性,但没有公式推导、算法设计和实验评价.此外,本文的分组随机化是文献[22]PN/g模型的更一般情况,分组内人数可以不同.本文理论上推导了支持度重构递归公式,基于递归公式设计了完整的分组随机化隐私保护频繁项集挖掘算法,并基于大规模合成和真实数据集,针对支持度重构误差和隐私保护性能,与已有的mask,emask,RE 方法进行了实验对比和评价,验证了方法的有效性.

事实上,隐私保护的内涵决定了其首要目标是为个体提供其所要求的保护,而差异化保护正体现了这一内在目标.GR-PPFM 可在兼顾这种差异化保护要求的同时,保证正常挖掘任务的执行.实验结果表明:相对于已有单参数随机化mask 方法,GR-PPFM 不仅能满足不同群体多样化的隐私保护需求,加强随机化参数设置的灵活性,还能在整体隐私保护度相同情况下,提高挖掘结果准确性.

1 问题与架构

基于分组随机化的隐私保护频繁模式挖掘GR-PPFM 的总体架构如图1 所示,所解决的问题是:给定原始事务集D={D1,D2,…,Dn}和最小支持度阈值min_sup,如何利用M1,M2,…,Mn共n个随机化模型,分别对D1,D2,…,Dn随机化,以及如何对随机化生成的事务集进行挖掘,得到跟集合F尽可能接近的频繁项集集 合,其中,F为从D挖掘得到的频繁项集集合.

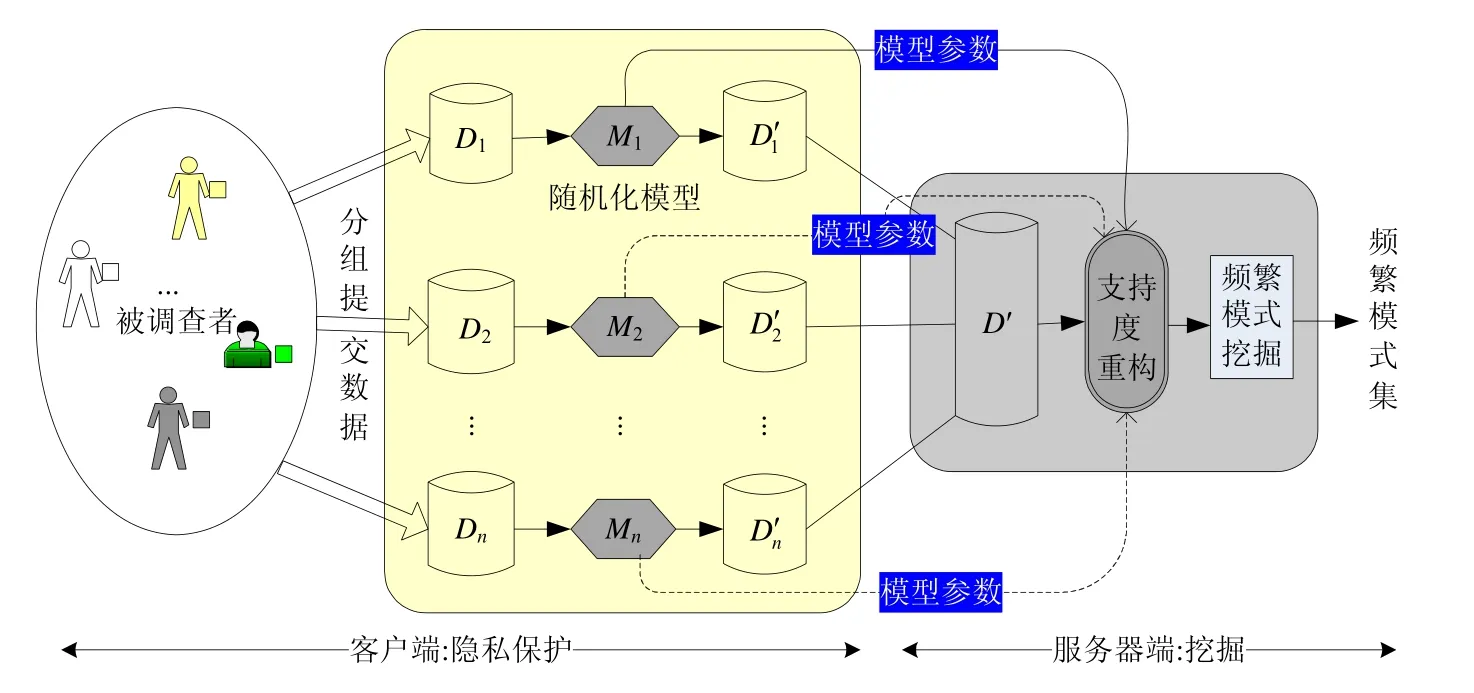
Fig.1 Framework of GR-PPFM图1 GR-PPFM 架构

GR-PPFM 分3 个阶段:(1) 数据分组;(2) 分组随机化;(3) 在支持度重构的基础上,进行频繁模式挖掘.

(1) 第1 阶段,隐私保护者对参与敏感问题的调查者(即数据提供者),按其对个人数据的保护程度要求进行分组,保护要求相同的进入同一组.可以预先设置若干个保护级别,被调查者可根据个人偏好选择一个合适的保护级别,一个级别对应一个分组.如图1 所示,共有n个保护级别供用户选择,分组后形成了D1,D2,…,Dn共n组数据.假定隐私保护者已根据先验知识,设计好若干个不同的隐私保护级别和对应的分组供被调查者选择,并假设参与调查的个体对其隐私保护取向都比较明确,能够通过引导选定其想要的保护级别和“找到队伍”;

(2) 第2 阶段,隐私保护者在客户端运用随机化模型,对分组后的数据分别进行随机化,生成随机化后的数据集.如图 1 所示,利用M1,M2,…,Mn共n个随机化模型,对D1,D2,…,Dn随机化,生成相应的共n个随机化数据集.具体的随机化过程和参数设置在第2.1 节给出;

(3) 第3 阶段,频繁模式挖掘者在服务器端,对随机化后的数据集D′进行挖掘,生成想得到的频繁模式集.数据集D′由共同组成.为了保证从随机化后的数据集能挖掘出正确的频繁模式,以得到 正确的关联分析结果,一个很重要的部件是结合随机化模型参数进行项集支持度的重构,第2.2 节讨论支持度重构.

上述GR-PPFM 架构中,被调查者本人对持有的数据随机化,随后将随机化数据传给频繁模式挖掘服务器.

2 分组随机化与挖掘方法

2.1 分组随机化

GR-PPFM 分组随机化的基本思想是由参与调查的个体自行决定对其数据的隐私保护级别和相应的随机化参数,隐私保护级别差不多的分为一组,同一组内共用同一个随机化参数,可表示为如下形式:

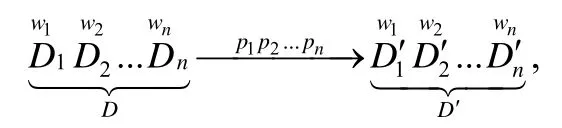
其中,原始事务集D由N个事务(个体)的m个项构成二维N×m布尔矩阵(数值属性可通过离散化变为分类属性,而分类属性又可变为布尔属性,即一般数据都可变为二维布尔矩阵形式).D1,D2,…,Dn为D中的n个数据分组,分组中的个体数占总个体数|D|=N的比例分别为w1,w2,…,wn(0＜wg＜1,g∈{1,...,n}).此n个数据分组分别以p1,p2,…,pn的概率进行随机化,生成随机化后的数据分组,共同组成频繁模式挖掘所用的事务集D′.每个Dg的随机化都遵循单参数随机化的基本过程,即:对该分组对应的N×m矩阵中的所有0-1 元素,均以pg的概率取原值,以1-pg的概率取反.单参数随机化使用随机化参数p与1-p具有对等效果(隐私保护度和挖掘结果准确性关于p=0.5 对称,p=0.5 隐私保护能力最强,但误差无穷大),故以下假定随机化参数均大于0.5.

表1 给出了个体分组随机化的例子.表的左边为原始事务集,由10 个被调查者的4 个问题项(I1/I2/I3/I4)组成,10 个被调查者分为5 组,分别包含3 个、2 个、2 个、2 个、1 个被调查者.同一组内隐私保护需求相同,对应的随机化参数分别为1,0.9,0.8,0.7,0.6.表的右边为分组随机化后的数据集,其中,前3 行为第1 组数据,这3 名被调查者完全不考虑隐私保护,愿意全部贡献原始数据,随机化概率参数p1=1;相反,由被调查者10 构成的第5 组数据非常在乎隐私,选择的随机化参数p5=0.6,其数据随机化时以0.6 的概率保持不变,以0.4 的概率取反.得到的最后一条记录中,有2 个值保持不变、2 个值取反.被调查者4-5,6-7,8-9 的隐私保护需求介于第1 组和第5 组之间,随机化参数在0.6 到1 之间.

Table 1 Grouping randomization of with GR-PPFM method 表1 GR-PPFM 方法分组随机化

GR-PPFM 方法采用分组多参随机化,允许对不同的人群使用不同的随机化参数,问题和挑战在于:

(1) GR-PPFM 对不同个体采取不同的随机化参数后,能像单参数随机化mask 一样重构出原始事务集中各项集的支持度吗?如何重构呢?第2.2 节针该问题给出解决方法;

(2) GR-PPFM 能从个体分组多参随机化模型中,得到真正的益处吗?第3 节实验评价将针对该问题作答.

2.2 支持度重构

2.2.1 基本原理

设I={I1,I2,...,Im}是一组项的集合,D={T1,T2,...,TN}为事务数据库,其中,事务Tu(u∈{1,2,…,N})为I的子集.项集A⊆I的长度|A|是指A中项的个数,如果|A|=k,则称A为k-项集.项集A在D中的支持计数(简称支持数)是指D中包含A的事务数,记作support_count(A)或SA,SA=|{Tu|A⊆Tu,Tu∈D}|.同时,将D中恰等于A的事务数,称作项集A在D中的净计数,记作CA,CA=|{Tu|A=Tu,Tu∈D}|.

假定A={I1,I2,…,Ik}为k-项集,根据mask 方法支持度重构原理,只要给出k-项集A的变换概率矩阵Pk=[pij],就可根据文献[22]中的公式(3):

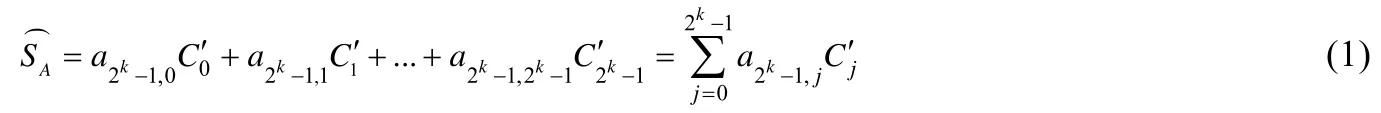
估算出项集A的重构支持计数.而公式(1)中,为矩阵Pk的逆矩阵中的最后一行元素,为A的第j个子集在D′(I1…Ik)中的净计数(即D′(I1…Ik)中恰等于第j个子集的事务数).因此,只要求出变换概率矩阵Pk,就可求得任意项集的重构支持计数和支持度了.因为求得Pk就可得到,进而得到aij.

2.2.2 变换概率矩阵

根据文献[22]表1,易推出单参数随机化4-项集的变换概率矩阵,见表2.

Table 2 Transition probability matrix P4 of mask 表2 mask 变换概率矩阵P4

对于表1 的分组多参随机化,如何求得变换概率矩阵P呢?文献[22]的公式(5)给出了PN/g模型pij的计算公式.PN/g模型每个分组记录数相同,而本文表1 每个分组记录数不同,但仔细分析发现,文献[22]的公式(5)同样适用于分组记录数不同的随机化.不过,文献[22]的公式(5)各组权重角标所用的组号i,容易 与pij中的角标i混淆,本文使用wg和pg,分别表示第g个分组所占的比例权重和对应的随机化参数,得到GR-PPFM 方法中k-项集A对应的2k×2k变换概率矩阵Pk中的元素值:

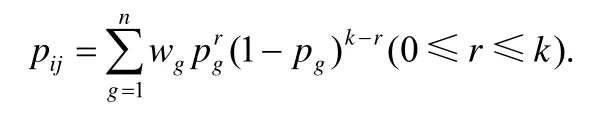
例如表1 中的分组随机化,事务“0000”转变“0000”的概率为

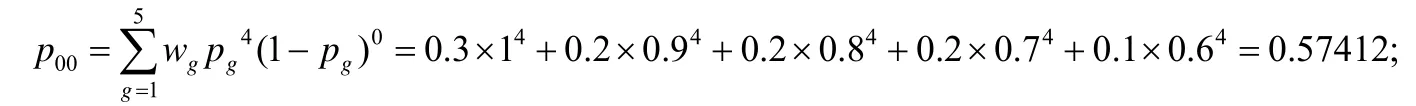
而“0001”(对应事务{I4})转变为“1110”(对应事务{I1I2I3})的概率为

这样便可得到4-项集{I1I2I3I4}对应的16×16 变换概率矩阵P4中的所有元素,见表3.

Table 3 Transition probability matrix P4 of GR-PPFM 表3 GR-PPFM 变换概率矩阵P4

在得到矩阵Pk后,就可根据,求得k-项集A的支持计数了,其支持计数恰等于向量中的最后一个元素.

文献[22]第3.3 节、第3.4 节给出了手工进行支持度重构的完整例子.

2.2.3 支持计数重构递归公式

有两种方法可加快求解整个项集空间的2m个项集支持度的计算过程:第1 种方法是根据求取2m个项集在D中的净计数,然后由项集的支持计数与净计数的关系求得此2m个项集的支持计数;第2 种方法是导出项集支持计数重构递归公式,见后文公式(4),根据该递归公式只需2m次求解,便可求取整个项集空间的2m个项集的支持度.下面给出公式(4)的推导过程:

2.3 GR-PPFM挖掘方法

GR-PPFM 利用支持数重构递归公式(4),在频繁项集生成算法Apriori 基础上形成,支持数重构递归公式是算法的核心,Apriori 构成了方法的主框架.

算法.分组随机化隐私保护频繁项集生成方法GR-PPFM.

输入:分组多参随机化数据D′;分组比例和随机化参数(pg,wg)(g=1,…,n);最小支持度阈值min_sup;

输出:从D′重构出的频繁项集集合.

3 实验评价

3.1 实验数据

分别用人工合成购物篮数据集、真实购物篮数据集进行实验评价.

人工合成购物篮数据集.人工合成购物篮数据集D由IBM Almaden 生成器生成,生成器参数为T=3,I=4,|D|=100K,N=10,即事务平均长度为3,频繁项集的平均长度为4,总事务数为100K,总项数为10.直接生成的数据集为项集形式,可将其转化为0,1 布尔表示的数据集;

真实购物篮数据.真实购物篮数据集D为某食品超市的购物数据basket.txt,事务平均长度为3,总事务数940,总项数为 11,包括fruitveg,freshmeat,dairy,cannedveg,cannedmeat,frozenmeal,beer,wine,softdrink,fish,confectionery.该数据可从以下网址获取:https://download.csdn.net/download/lol000/8693253(2020 年2 月).

3.2 实验方法

• 第1 步,挖掘原始数据集D.

针对多个不同的最小支持度阈值,分别运用Apriori 算法对数据集D进行挖掘,记录每次挖掘得到的所有频繁项集和其支持数.

• 第2 步,生成分组多参数随机化数据集.

对数据集D进行分组多参数随机化干扰,生成干扰后的数据集D′.具体地讲,对数据集D按行分为Group1～ Group5 共5 组数据,这5 组数据所占的比例分别为w1=30%,w2=20%,w3=20%,w4=20%,w5=10%,对应的随机化参数分别为p1=1,p2=0.9,p3=0.8,p4=0.7,p5=0.6.即:第1 组数据保持不变;第2 组数据以0.9 的概率保持原来的值,以0.1 的概率取反;第3 组～第5 组数据分别以0.8,0.7,0.6 的概率保持原值,以0.2,0.3,0.4 的概率取反.直观地,数据集D对应的分组多参随机化模型参数设置见表4.

以上5 组数据所占比例,大致依据本文开始提到的AT&T 实验室1999 年隐私态度调查报告中不同用户的比例和进一步细分.隐私保护级别设置大致遵从国家保密局2007 年6 月22 日颁布的《信息安全等级保护管理办法》中的五级分类.表4 中:1 级表示信息密级为公开,不需保护;2 级表示信息密级为限制,需弱保护;3 级表示信息密级为秘密,需保护;4 级表示信息密级为机密,需强保护;5 级表示信息密级为绝密,需特别强的保护.5 级分类不仅考虑了信息保护需求的差异性,同时级数设置较少易于管理,实际中也可根据需要进一步分级细化.

• 第3 步,生成单参数随机化数据集.

为便于同单参数mask 方法对比,对数据集D进行单参数随机化干扰,生成mask 方法所用的单参数随机数 据集,随机化概率p设置为多参数随机化的平均概率,即:

• 第4 步,挖掘随机化数据.

针对多个不同的最小支持度阈值,分别运用Apriori 算法以及带有支持数重构的GR-PPFM 方法,对第3 步生成的多参数随机化数据集D′进行挖掘,记录每次挖掘得到的所有频繁项集和其支持数.同时,运用Apriori 算 法和mask 方法,对第4 步生成的单参数随机化数据集挖掘,记录挖掘得到的频繁项集和对应的支持数.

• 第5 步,计算分析误差.

对比第4 步的挖掘结果,计算分析mask 方法、GR-PPFM 方法的挖掘结果误差,包括项集支持度相对误差ρ、项集身份误差θ-和θ+.其中,ρ反映频繁项集在随机化数据中重构后的支持度与其在原数据中的实际支持度间的相对误差;θ-表示频繁项集丢失率,衡量原先频繁而被错误识别为不频繁的项集占原频繁项集总数的比例;θ+表示频繁项集增加率,衡量原先不频繁而被错误识别为频繁的项集占原频繁项集总数的比例.具体公式见文献[1].

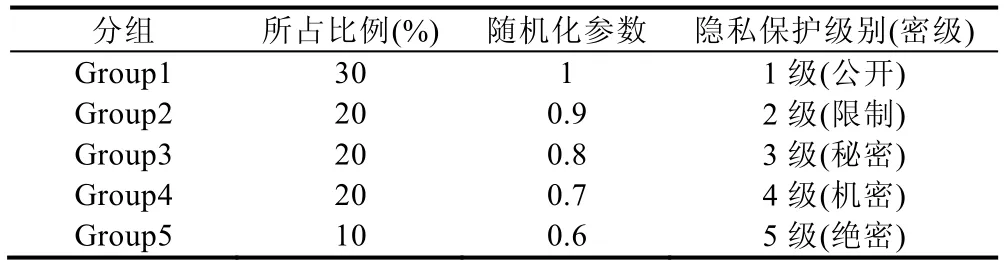
Table 4 Randomization parameter settings of dataset D表4 数据集D 的随机化模型参数设置

3.3 结果分析

本节对实验结果分析,考察不同方法挖掘结果的误差随项集长度k、最小支持度阈值min_sup 的变化情况,并对不同方法的误差进行对比.其中,图2 为合成数据上的实验结果,图3 为真实数据上的实验结果.

3.3.1 误差与项集长度的关系

3.3.1.1 支持度误差

图2(a)给出了针对合成数据,当最小支持度阈值min_sup=0.1%时,mask 和本文GR-PPFM 方法的平均支持度相对误差ρ随频繁项集长度k的变化曲线.图3(a)给出了针对真实数据,当min_sup=1%时,ρ随k的变化曲线.

(1) 横向比较:很明显,本文提出的多参数随机化GR-PPFM 的误差小于单参数随机化mask 方法.说明了在 整体隐私保护度相同的情况下(实验中,mask 的随机化参数p等于多参数随机化的平均概率),GR-PPFM 挖掘结果好于mask;

(2) 误差随频繁项集长度k的变化:

a.理论上,从k-项集的支持度重构递归公式(4)分析,k-项集的重构支持度依赖于该k-项集的所有子集的重构支持度,作为一个递归的过程,的支持度依赖于,依此类推.这种递归依赖关系将导致误差的级联传导,使误差从1-项集逐渐向上层传递和累积,因此直观上,k越大,理论偏差也越大;

b.观察图2(a)发现,平均支持度相对误差随k大体呈现先上升、后下降的趋势.在频繁5-项集处,平均支持度误差最大,5-项集之前误差随k的增加而增大,5-项集之后误差大致平缓下降.为什么图中的误差在频繁5-项集后会出现回落呢?回到ρ的计算公式,不难发现,ρ计算的是频繁项集的平均支持度相对误差,这意味着ρ与最小支持阈值min_sup 紧密相关.因为min_sup 不同,其划定的某个长度的频繁项集集合F也就不同,造成该集合的平均支持度误差ρ也会不同.这表明,F对应的ρ值会因特定数据的偏斜和最小支持度阈值min_sup 的不同而出现偶然变大变小的情况.因为F中即使出现1 个误差特别大或特别小的项集,就能显著改变F的平均支持度误差ρ值,尤其当F中的项集个数较少时.

图2(a)中,在min_sup=0.1%时,原始数据对应的频繁1-项集集合、2-项集集合、…、8-项集集合的项集个数依次为10,44,112,160,125,40,8,1.其中,频繁4 项集的个数最多(这是IBM Almaden 生成器生成的数据集特征决定的,因为选取的参数指定了生成数据集的频繁项集的平均长度为4),而频繁6-项集、7-项集和8-项集集合的个数较少,尤其是频繁8-项集集合,只有1 个项集,因此其平均支持度误差的偶然性就较大,这也是图中5-项集以后误差回落的原因.当F中的项集个数较多时,偶然性因素会被淹没,误差大小会顺从一般的规律随项集长度的增加而增大.事实上,实验中发现:当设置min_sup=0.001%时,即只要出现1 次的项集就为频繁项集(因为实验所用的数据集D的大小为100 000)时,所测得的ρ正是按项集长度的递增而递增的.因为此时每一级长度对应的频繁项集个数都较多,平均误差随项集长度的变化能呈现理论分析的规律.

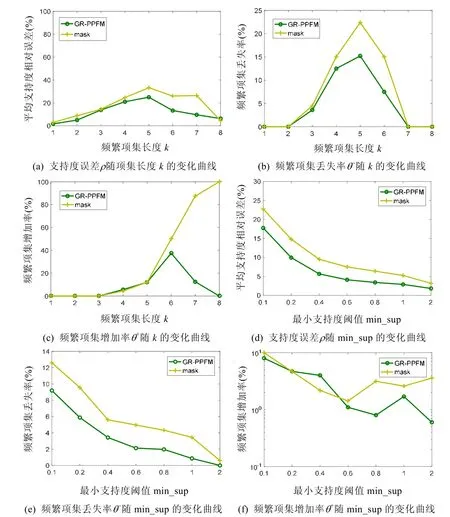
Fig.2 Experiment error of mask,and GR-PPFM on synthetic data图2 mask、GR-PPFM 在人工合成数据中的实验误差

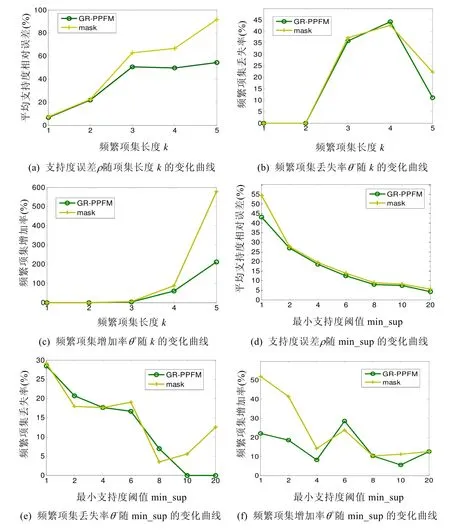
Fig.3 Experiment error of mask and GR-PPFM on real-world data图3 mask 与GR-PPFM 在真实数据中的实验误差

图3(a)测得的ρ正是按项集长度的递增而递增的,同理论分析一致.

3.3.1.2 项集身份误差

图2(b)、图3(b)和图2(c)、图3(c)给出了项集身份误差随频繁项集长度k的变化情况,可以看出:(1) 分组随机化GR-PPFM 方法误差小于单参数随机化mask 方法;(2) 项集身份误差随k的变化跟图2(a)、图3(a)中支持度误差ρ随k的变化情况相近,误差大致随k增大而增大.

θ-,θ+随k变化规律与ρ随k变化规律的相似性是容易理解的,因为追根溯源,项集支持度大小决定了项集作为频繁项集还是非频繁项集的身份,项集支持度误差从最深层次反映了随机化过程对于数据的影响,项集身份误差是项集支持度误差的外在表现.

3.3.2 误差与支持度阈值的关系

3.3.2.1 支持度误差

图2(d)给出了合成数据所有频繁项集(从频繁1-项集到频繁8-项集,k=ALL)的平均支持度相对误差ρ随最小支持度阈值min_sup 的变化曲线.图3(d)给出了真实数据上ρ随min_sup 的变化曲线.

(1) 横向比较:横向比较图2(d)、图3(d)可发现:误差大小关系跟图2(a)、图3(a)一致,仍是GR-PPFM＜mask.说明在整体隐私保护度相同时,多参数随机化方法GR-PPFM 的挖掘结果优于单参数mask 方法;

(2) 误差随支持度阈值min_sup 的变化:观察曲线随min_sup 的变化可发现,平均支持度误差随支持度阈值的增大而减小.说明随着支持度阈值的增大,挖掘结果越好.原因是什么呢?由于支持度相对误差等于绝对误差与原始支持度值的比值,假定项集I1和I2的绝对误差相等,则项集I1和I2的相对误差完全取决于其原支持度值:原支持度值越大,其相对误差越小;原支持度值越小,其相对误差越大.当支持度阈值增大时,其对应的频繁项集集合F中各项集的支持度相对越大,造成F中各项集的平均支持度相对误差越小,误差随min_sup 的变化呈现图2(d)、图3(d)中的趋势.

3.3.2.2 项集身份误差

图2(e)、图3(e)和图2(f)、图3(f)给出了项集身份误差随支持度阈值min_sup 的变化情况.可看出,项集身份误差随min_sup 的变化跟图2(d)、图3(d)支持度误差ρ随min_sup 的变化情况大体相近,其基本规律:(1) 大多数情况下,分组随机化GR-PPFM 方法的误差小于单参数随机化mask 方法;(2) 误差随min_sup 增大而减小.θ-,θ+随min_sup 变化规律与ρ随min_sup 变化规律相似.

3.3.3 支持度重构与不重构误差对比

通常,数据随机化后,由于数据被扰乱,项集的支持度将发生变化,若直接从随机化后的数据挖掘,不进行支持度重构,项集的支持度跟原始支持度比究竟会发生多大的变化呢?图4(a)～图4(d)分别给出了实验中针对合成数据和真实数据、单参数随机化mask(随机化概率p=0.84)支持度重构与不重构的误差对比及分组随机化GR-PPFM 支持度重构与不重构误差对比.图4 中,合成数据、真实数据设置的最小支持度阈值分别为0.1%,1%.

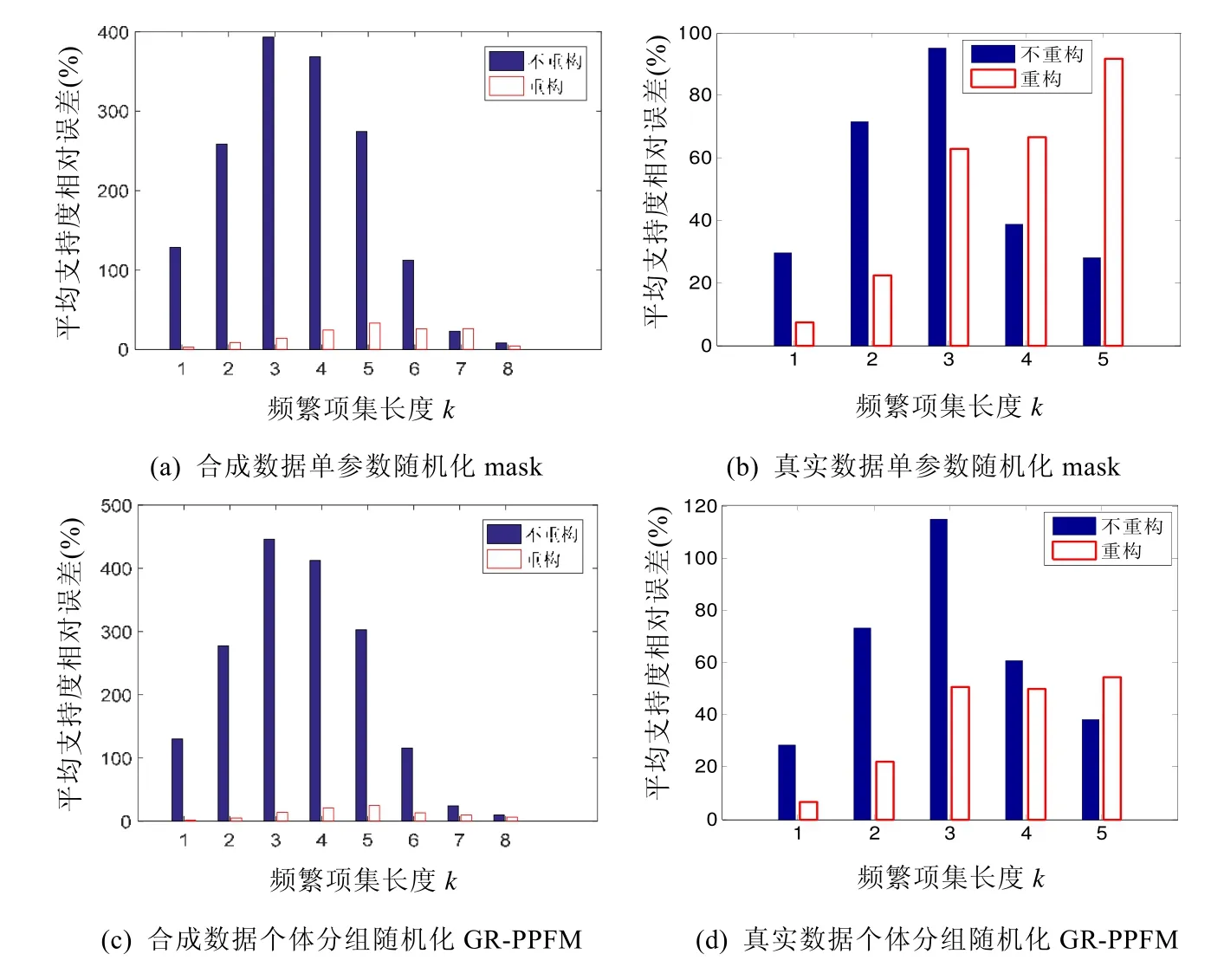
Fig.4 Error of support reconstruction vs.non-reconstruction图4 支持度重构与不重构误差对比

图4(a)、图4(c)针对IBM Almaden 生成器生成的数据,可发现支持度不重构的误差远远大于重构误差.说明数据经随机化后,项集的支持度已发生显著变化,直接从随机化后的数据得到的挖掘结果已远远偏离从原始数据挖掘得到的结果,必须通过支持度重构恢复原数据库中各项集的支持度,以得到跟原数据尽可能相近的挖掘结果.

图4(b)、图4(d)针对真实购物篮数据,可发现当频繁项集长度不大时,不重构的误差远远大于重构误差;但当频繁项集长度较大时(单参数随机化后k=4,5,分组随机化k=5),不重构的误差反而小于重构的误差.说明对于高阶项集重构的误差大,这跟之前分析的误差随k增大而增大的规律一致.综合图4,针对分组随机化,对于低阶项集(k＜5)使用重构支持度,对于高阶项集(k≥5)使用不重构支持度.

3.3.4 隐私保护对比

下面分析两种方法的隐私保护性能,从隐私保护度(定量)、个体隐私保护差异性和暴露的信息(定性)等方面进行对比.本文隐私保护性能考虑的场景是敏感问题调查或购物时,对于敏感问题回答为“是”和“购买”敏感物品的保护,不考虑对于敏感问题回答为“否”和“不购买”敏感物品的保护.并假定被调查者运用随机化装置给出了真实的回答,购物数据提供者对数据进行了相应的随机化变换.

3.3.4.1 隐私保护度

文献[10]将单参数随机化mask 的隐私保护度privacy定义为1-R(p),其中,R(p)=aR1(p)+(1-a)R0(p).其中,R1(p)表示原始数据库中的“1”能从随机化后的数据库中被还原的概率,R0(p)表示原始数据库中的“0”能从随机化后的数据库中被还原的概率,a为隐私保护权重.本文隐私保护场景只考虑敏感问题回答为“是”和“购买”敏感物品记录的保护,即对如表1 所示的0-1 购物篮数据,只考虑“1”值的保护.设保护权重系数a=1,则隐私保护度公式为

假定随机化概率为p,项的平均支持度为s0,R1(p)的计算公式为

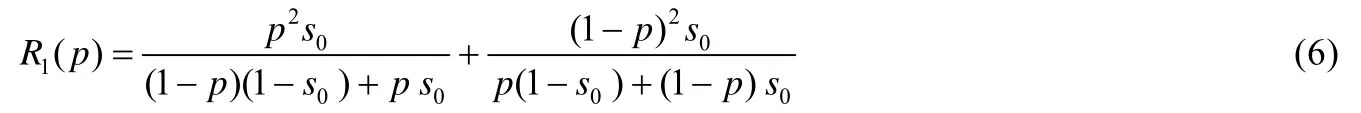
根据公式(5)、公式(6)的分析,隐私保护度1-R1(p)跟p(p＞0.5)和s0均成反比.说明随机化概率越大,项的平均支持度越高,隐私保护度越低;反之亦然.极端地,当p=1 时,数据完全保持不变,R1(p)=1,隐私保护度最低,为0.

• 当s0=1 时,数据是全1 数据,R1(p)=1,隐私保护度也是最低,为0.此时,无论p取多少,“1”均能从随机化后的数据中被还原,随机化均无法保护数据;

• 当s0=0 时,数据是全0 数据,R1(p)=0,隐私保护度最高,为1.

对于分组随机化,由于不同分组随机化概率p不同,所以不同分组的隐私保护度也不同.假定wg为第g个分组个体数占总个体数的比例,pg为第g个分组对应的随机化概率,R1(pg)为第g个分组中的“1”能从随机化后的数据库中被还原的概率,privacy(g)=1-R1(pg)为第g个分组对应的隐私保护度.对于分组随机化,在已知每个分组对应的随机化概率的条件下,定义如下4 个隐私保护度:最低隐私保护度、最高隐私保护度、平均隐私保护度、整体隐私保护度.

定义1(最低隐私保护度minPrivacy).分组随机化中,隐私保护度最小的分组对应的隐私保护度.公式为

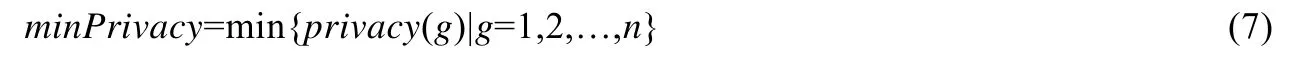
定义2(最高隐私保护度maxPrivacy).分组随机化中,隐私保护度最大的分组对应的隐私保护度.公式为

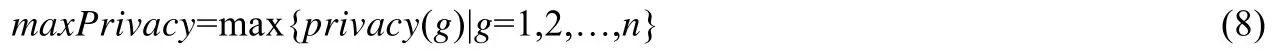
定义3(平均隐私保护度avgPrivacy).分组随机化中,多个分组隐私保护度的平均值称为平均隐私保护度.计算公式为

定义4(整体隐私保护度overallPrivacy).将分组随机化的平均概率代入公式(5),求得的隐私保护度称为 整体隐私保护度.计算公式为

实验中,IBM Almaden 生成器生成的合成数据中,项的平均支持度s0=40.69%;真实数据中,项的平均支持度s0=27.08%.项的平均支持度s0取决于原数据,事实上,由于原数据是无法知道的,真实的s0无从得知,实际中,可通过先验知识或抽样估计s0值,也可通过重构得到的项的平均支持度代替s0值.将s0和p1=1,p2=0.9,p3=0.8,p4=0.7,p5=0.6,=0.84 代入公式(5)～公式(10),可分别求得合成数据和真实数据分组随机化时,在已知每个分组对应的 随机化概率的条件下,GR-PPFM 对应的最低隐私保护度、最高隐私保护度、平均隐私保护度和整体隐私保护度,结果见表5.

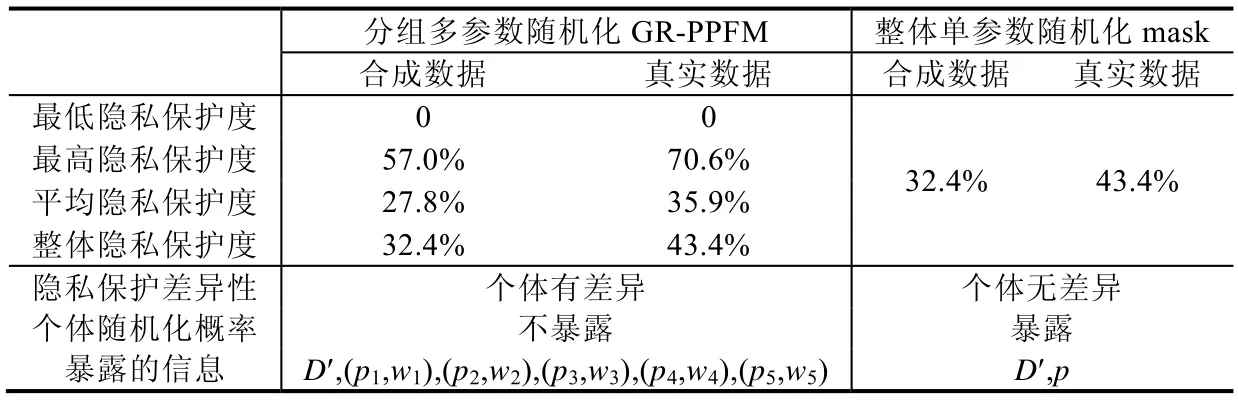
Table 5 Privacy of GR-PPFM vs.mask表5 GR-PPFM 与mask 方法隐私保护性能对比

单参数随机化mask 仅对应一个隐私保护度,实验中,单参数mask 方法的随机化概率p=0.84,分组多参随机 化的平均概率=0.84,两者相等.因此,单参数随机化的隐私保护度与分组随机化的整体隐私保护度相同,合成 数据是32.4%,真实数据是43.4%.

3.3.4.2 隐私保护差异性

除定量考察隐私保护度外,还可定性分析两种方法对个体隐私保护的差异性及为支持度重构需暴露的信息的差异.GR-PPFM 对个体实施有差异的保护,而mask 实施无差异的保护.

从个体对应的随机化概率是否暴露给挖掘者来分析.在分组随机化GR-PPFM 方法中,为了进行支持度重构,挖掘者只需要知道个体大致使用了哪些随机化参数以及相应的个体比例,而不需要知道具体的个体与使用的随机化参数的确切对应关系.但mask 支持度重构需要知道p,由于所有的个体都使用了同样的p,所以挖掘者确切知道每个个体与随机化参数的对应关系,即任意指定一个个体,挖掘者都能确切知道该个体使用了什么样的参数进行了随机化变换.

两种方法的隐私保护度、隐私保护差异性和为支持度重构需要暴露的信息见表5,其中,D′表示D随机化后 的全部数据,表示D中以pg的概率随机化后的第g组数据,其占全部数据的比例为wg.实验中,p1=1,p2=0.9,p3=0.8,p4=0.7,p5=0.6;w1=0.3,w2=0.2,w3=0.2,w4=0.2,w5=0.1.

3.4 拓展实验

为进一步探究本文工作GR-PPFM 与其他相关工作的效能差异,本节设计实验对GR-PPFM,emask 和RE 这3 种算法进行对比.GR-PPFM 按行分组随机化,emask 对0,1 分别随机化,RE 按列分组随机化,实验数据采用第3.1 节提到的真实购物篮数据,GR-PPFM 采用第3.2 节实验方法第2 步使用的分组比例和相应的随机化参数设 置,平均随机化概率=0.84.Emask 设置两个随机化参数:p1=0.6,p0=0.9,即:对所有的“1”值,以0.6 的概率保持不 变,以0.4 的概率取反;而对“0”值,则以0.93 的概率保持不变,以0.07 的概率取反.由于“1”和“0”在数据中的占比 分别为72.9%和27.1%,平均随机化概率=0.6×72.9%+0.93×27.1%=0.84.RE 将购物篮数据中的11 种商品分为 3 组:(1) fruitveg,freshmeat,dairy;(2) cannedveg,cannedmeat,frozenmeal,beer,wine;(3) softdrink,fish,confectionery.第(1)组～第(3)组随机化参数分别设为0.68,0.84,1,平均随机化概率=(3×0.68+5×0.84+3×1)/11=0.84.3 种方法的 平均随机化概率均为0.84,保证三者的整体隐私保护度相同.图5 给出了GR-PPFM,emask 和RE 这3 种方法在整体隐私保护度相同的情况下挖掘结果的差异.

Fig.5 Support error of GR-PPFM/emask/RE on real-world basket data图5 GR-PPFM/emask/RE 在真实购物数据中的支持度误差

图5(a)为支持度阈值1%时,支持度相对误差随挖掘出的频繁项集长度变化的比较;图5(b)为支持度误差随最小支持度阈值变化的比较.可以看出:在整体隐私保护度相同情况下,本文提出的个体分组随机化GR-PPFM的误差均小于相关工作提到的0,1 差异随机化emask 方法及属性分组随机化RE 方法.

4 总结与展望

已有以mask 为代表的隐私保护频繁模式挖掘方法,在对数据随机化时,采用统一的随机化参数,对所有个体实施同等、无差异的保护.考虑到不同人群对隐私保护需求的差异性,本文提出一种基于分组随机化的隐私保护频繁模式挖掘GR-PPFM 方法.针对GR-PPFM,探索了支持度重构方法以及与之相适应的频繁模式挖掘算法,实现了粗粒度的个性化隐私保护频繁模式挖掘.实验结果表明:

(1) 在整体隐私保护度相同情况下,分组随机化GR-PPFM 挖掘结果准确性高于整体单参数随机化mask;

(2) 分组随机化对不同人群实行有差异的保护,个体隐私保护度更强,为支持度重构暴露的信息更少;

(3) 支持度重构误差随项集长度的增大而增大、随支持度阈值的增大而减小,支持度重构误差远远小于直接挖掘不重构的误差.

本文的贡献在于,基于不同人群隐私保护需求不同的事实,提出了分组多参数随机化的数据保护方式;给出了分组随机化的支持度重构方法以及与之相适应的频繁模式挖掘算法,实现了粗粒度的个性化隐私保护频繁模式挖掘;实验分析比较了分组多参数随机化和单参数随机化两种方法的效果.

GR-PPFM 方法可广泛应用于社会、经济生活中涉及隐私的敏感性问题的调查和关联分析任务.未来工作包括:(1) 探索误差随分组参数w、随机化概率参数p和数据集大小参数|D|的变化情况;(2) 本文只通过实验证实了分组随机化GR-PPFM 方法的可行性及相对于单参数随机化mask 方法的优越性,能否从理论上导出两种方法k-项集的支持度重构偏差公式,并证明GR-PPFM 方法的优越性值得探究;(3) 能否将分组随机化模型应用到其他类型的个性化隐私保护挖掘算法,如分类、聚类[23],并构造与之适应的特征重构方法,也是十分值得期待的研究工作.