基于动态赋权近邻传播的数据增量采样方法*
陈晓琪,谢振平,刘 渊,詹千熠
1(江南大学 人工智能与计算机学院,江苏 无锡 214122)
2(江苏省媒体设计与软件技术重点实验室(江南大学),江苏 无锡 214122)
现代信息技术的不断发展和进步,使各个领域累计了大量的数据,广泛涉及图像、文本、音频以及其他各类非结构化数据等.面对海量规模增长的数据内容,如何更有效地平衡信息获取的效率和有效性,正成为大数据处理的新重要问题.数据采样(data sampling)技术是一种能够在一定程度上解决上述问题的手段之一,该技术考虑从数据集中选取有代表性的样本作为整个数据集合的代表,在减小数据规模的同时,最大可能地保留数据集的有用信息,从而精简地表达数据集合包涵的重点知识.
当前,与数据集代表点采样相关的研究更多的是围绕图像数据.文献[1]提出了多字典不变稀疏编码方法,在不依赖人工标记、种子图像或其他先验知识的情况下,采集互联网上的代表性商标图像,为商标识别、商标侵权检测、品牌保护等领域自动提供原型、代表性图像或弱标签训练图像.文献[2]使用图像位置信息和图像相关标记,基于上下文和内容挖掘与位置和标记视觉相关联的图像,结合k-means 聚类方法从视觉相关图像中选择代表性图像,为世界著名标志性建筑提供浏览摘要.文献[3]基于情感特征生成图像摘要,通过概率情感模型提取输入图像情感特征,在情感空间中对图像做聚类处理,结合覆盖性、情感一致性和显著性对簇排序并选择代表性图像.文献[4]提出一种区别于大多数利用视觉特征系统的基于语义知识的图像集合摘要方法,其通过图像间的语义相似度构建语义相关性网络,依据网络中心性选择代表性图像.文献[5]将图像自动摘要问题看作稀疏表示的字典学习问题,将图像摘要任务看作是字典学习任务,去实现大规模图像数据集的代表性图像选择.
现有的代表点采样方法大多基于聚类[6-9]方法,通常可抽象为3 个步骤:(1) 用一组特征向量来表示数据集中的样本点,数值类型数据应用简单处理可转化为特征向量,图像数据则根据自身特点结合特征提取方法表示为一组高维特征向量;(2) 在特征向量空间中,采用聚类方法将样本点划分为若干簇;(3) 利用样本点代表性排序方法,从簇中选择具有代表性的样本.代表点采样方法可以从数据表示、聚类方法和代表点选择方法这3 个方面进行研究.针对样本点聚类和代表点排序,常用的方法是使用AP(affinity propagation)算法[6,7,10,11]进行代表点的选择.与传统聚类算法相比,AP 算法不需要预先设定聚类个数,对初始值不敏感,并且其生成的聚类中心是数据集中真实存在的样本点,不仅具有很好的代表性,且可以直接将聚类中心当作簇代表点.尽管AP 算法在处理许多问题上具有优势,但它一个较大的不足是算法复杂度较高,在Frey 等人所做的代表性灰度图像选择实验中[12],运行1 次AP 算法所消耗的时间与运行100 次k-center 算法所消耗的时间基本相同.与K-means 算法相比,AP 算法的时间复杂度正比于数据规模的平方,而k-means 算法的时间消耗则是线性增长.当数据规模较大时,AP 算法的计算时间将很长,且对存储空间要求也呈平方规模增长,这极大地限制了AP 算法应用于大规模数据处理的实用性.
针对大规模数据的代表点采样问题,本文提出了一种基于动态赋权近邻传播的数据增量采样算法ISAP (incremental data sampling using affinity propagation with dynamic weighting).主要包含两个策略.
(1) 近邻传播偏向参数的动态赋权.在AP 算法的迭代过程中,利用样本点单次迭代聚类结果计算样本点自身轮廓系数,对AP 算法的重要参数——偏向参数做动态调整,使最终采样结果能够包含更多的潜在性样本;
(2) 引入分层增量处理,将数据集划均匀划分为规模适中的子集,在各子集上分别执行全局偏向参数动态赋权的AP 算法,获得局部最优代表点集合;然后在局部最优代表点集合上执行局部偏向参数动态赋权的AP 算法,推选出整个数据集的最终代表点.
相比于现有的主要增量采样算法[13,14],它们的主要目的在于实现数据密度上的均匀采样.而ISAP 算法目的在于实现数据空间上基于聚类划分的代表性样本获取.
为检验ISAP 算法的性能及其在图像数据应用问题的价值,我们分别在人工合成数据集、UCI 标准数据集和图像数据集上进行了代表性样本采样任务,对比一些经典的和较新的方法,结果表明:我们的方法与现有相关方法在采样划分质量上处于同一水平,而计算效率则获得了大幅提升.进一步将新方法应用于深度学习的数据增强任务中,相应的实验结果表明:在原始数据增强基础上,结合进高效增量采样处理后,训练数据多样性增加,在不改变总训练数据集规模的情况下,新方法介入所获得的模型质量可实现显著的提升.
本文的主要贡献:
(1) 提出了一种基于动态赋权近邻传播的数据增量采样算法,引入分层增量处理和样本点动态赋权策略,良好地实现了数据采样质量和效率的平衡;
(2) 在人工合成数据集、UCI 标准数据集和图像数据集上进行代表性样本采样任务,本文方法在提高采样效率的同时,保证了代表性样本的显著性和覆盖性;
(3) 将本文方法应用于深度学习的数据增强任务中,实验结果表明:在保持训练数据集规模不变的情况下,本文方法介入所获得的模型质量有显著提升.
本文第1 节将介绍方法框架.第2 节、第3 节介绍标准AP 算法及基于动态赋权近邻传播的数据增量采样算法ISAP.第4 节对算法进行相关分析.第5 节通过实验评估算法的效果.第6 节对本文进行总结,对未来工作进行展望.
1 基于动态赋权近邻传播的数据增量采样方法ISAP 框架
本文提出的基于动态赋权近邻传播的数据增量采样算法框架如图1 所示,主要包含以下内容.
(1) 动态赋权的AP 算法.本文提出一种用于代表点采样的动态赋权AP 算法,在AP 算法的迭代过程中,利用样本点单次迭代聚类结果计算样本点自身轮廓系数(silhouette coefficient),对样本点的偏向参数做动态调整,不断赋予新的权值直至方法收敛,使最终采样结果能够包含更多的潜在性样本;
(2) 分层增量采样.基于上述偏向参数动态赋权算法,结合整体样本点的全局初始偏向参数和局部代表点之间的相对于整体数据集的局部初始偏向参数,提出了分层增量的代表点采样算法ISAP.算法架构如图1 所示:首先,将样本集合划分为规模上大小均匀的子集,在每个子集上执行全局偏向参数动态赋权的AP 算法,得到每个子集产生的局部代表点,所有子集产生的局部代表点组成局部代表点集,本文将该过程称为增量局部推选层;然后,在局部代表点集上利用动态赋权AP 算法对局部代表点进行合并,产生数据集整体代表点,本文将该过程称为合并推选层;最后,将数据集中的非代表点划分给与其相似度最大的代表点,完成全局簇划分.
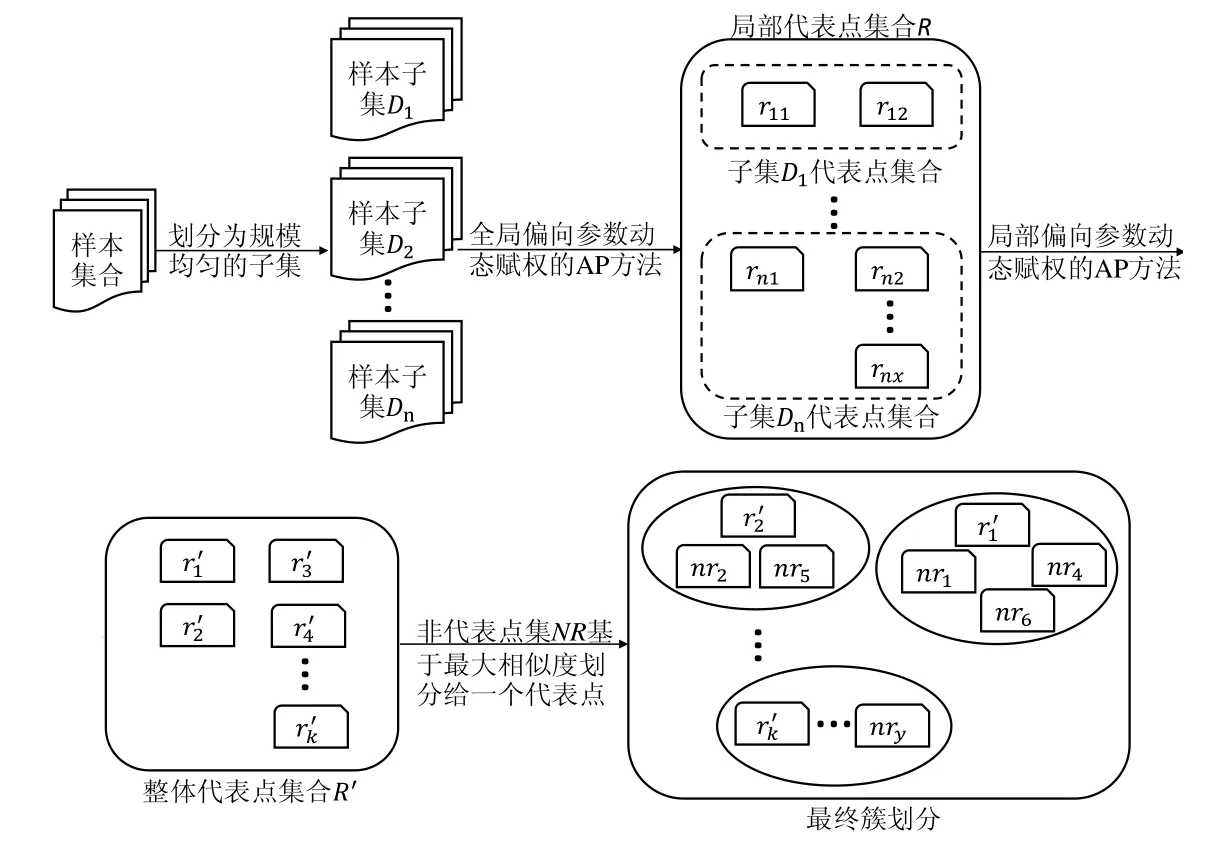
Fig.1 Flow chart of proposed incremental data sampling method图1 本文数据增量采样算法流程图
2 AP 算法中偏向参数的动态赋权
AP 算法[12]是一种exemplar-based 聚类方法,它将所有数据样本看作是网络中的节点,通过节点间的双向消息传递,收敛得到最优的簇代表点集合.AP 算法与其他聚类方法的最大不同点是:其生成的聚类中心是数据集中真实存在的样本,具有很好的代表性,可以直接作为簇的代表点.
在基于聚类方法的代表点采样问题中,聚类质量与代表点采样质量紧密相关,聚类质量的提升,在一定程度上能够解决采样结果的代表性问题.AP 算法改善聚类质量的一个方向是偏向参数,偏向参数直接影响最终聚类数目,决定聚类质量的好坏.偏向参数一般根据经验设置为统一常数[12,15,16],在AP 算法的迭代过程中恒定不变,即所有样本点成为簇代表点的可能性从始至终是一样的.但是在实际情况中,样本点之间的差异使得它们成为簇代表点的可能性不尽相同;此外,在迭代过程中因为信息交换的影响,样本点成为簇代表点的概率是会变动的.因此,给所有样本点设置同样且恒定的偏向参数的做法并不恰当,容易导致不好的聚类结果.为便于后续讨论,表1 中汇总给出了本小节与新方法有关的符号信息.

Table 1 Summary of relevant symbols on chapter 2表1 第2 节新方法相关符号汇总
2.1 初始偏向参数定义
在实际问题中,根据局部密度、语义性等信息可以知道,样本点成为簇代表点的可能性是有区别的,所以将偏向参数P={pk}1×N设置为统一常数的做法并不恰当.
为了充分考虑数据本身所蕴含的信息,减少信息迭代中不必要的计算,文献[17,18]依据数据集中样本点的分布情况,为每个样本赋予不同的初始偏向参数.本文方法仅考虑样本点在局部范围内与其他样本之间的平均相似度,不考虑比例系数的影响,采用如下初始偏向参数计算公式:

其中,
•I(·)为指示函数;
• 参数cutoff表示不等式s(i,k)≥θ的结果:如果s(i,k)≥θ成立,则I(cutoff)=1;否则为0.
参数θ定义为相似度截断值,其大小的设置与数据集所有样本点间的相似度紧密程度相关,其在某种程度上也反映了原始距离度量s(·,·)的上限合理尺度.
2.2 偏向参数动态赋权
标准AP 算法的输入是相似度矩阵S={s(i,j)}N×N以及包含在S中的偏向参数P={pk}1×N(s(k,k)←pk),pk表示样本点k被选为聚类中心的可能性.对于N 个样本点的聚类问题,AP 算法旨在找到一组聚类中心,将每一个非中心点分配给唯一的聚类中心,以便最大化非中心点和其聚类中心之间的相似性以及各聚类中心的偏向参数的总和.一种典型的AP 算法二元变量因子图[12]如图2(1)所示.

Fig.2 Factor graph of the AP method图2 AP 算法二元变量因子图及其改进后的因子图
在图2(1)中,{cij}N×N中的cij属于{0,1},cij=1 表示点j是点i的聚类中心.标准AP 算法需要满足两个聚类约束条件:一个是聚类中心的唯一性,即一个点只能属于一个类(图2(1)中约束I);另一个是聚类中心的存在性,即当一个点是另一个点的聚类中心时,该点必然是自己的聚类中心(图2(1)中约束E).基于这两个约束,AP 算法通过在因子图上的信息传递更新使得全局函数S(C)最大,其具体定义见公式(2).
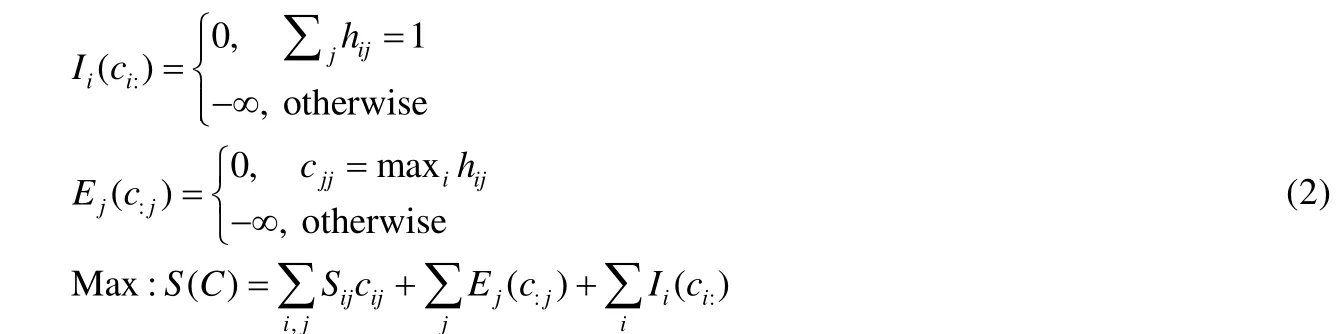
针对这一NP 难问题,依据max-sum 算法[12,19]可推导出AP 算法的迭代更新公式.在AP 算法中,有两种重要的消息在样本点间传递,分别是吸引度(responsibility)和归属度(availability),在算法中表现为吸引度矩阵R= {r(i,j)}N×N和归属度矩阵A={a(i,j)}N×N,其更新公式如下:

吸引度r(i,j)表示样本点j作为样本点i的聚类中心的合适程度,归属度a(i,j)表示样本点i选择样本点j作为聚类中心的合适程度.对于任意的样本点k,如果其对于自身的归属度a(k,k)和吸引度r(k,k)之和大于0,则样本点k是一个聚类中心.
从标准AP 算法的迭代过程和聚类中心选取方法可以看出,偏向参数P={pk}1×N(s(k,k)←pk)的大小直接影响最终聚类数目.在大多数基于AP 过程的算法中,各样本的pk被设为同一常数并且在迭代过程中保持不变.一旦pk被确定,聚类结果也就被确定下来,过程中没有其他的方法来对结果进行修正.为了降低初始pk对聚类结果的影响,可以引入额外的信息在聚类过程中动态改变偏向参数.本文考虑引入节点的轮廓系数对每一次迭代产生的中间结果进行评价,从而依据评价结果动态改变每个点的pk.即:当AP 算法产生至少一个聚类中心时,认为点与点之间产生了相互作用.依照这一思想,AP 算法的因子图模型结构将相应地发生变化,在原本的聚类约束条件下,将新增有关于聚类中心的约束,改变后的因子图模型及其信息传递如图2(2)所示.新的因子图新增了聚类约束条件F,该约束表示当产生至少一个聚类中心时,各节点之间存在相互作用,新增约束公式及改变后的全局函数S(C)如下:
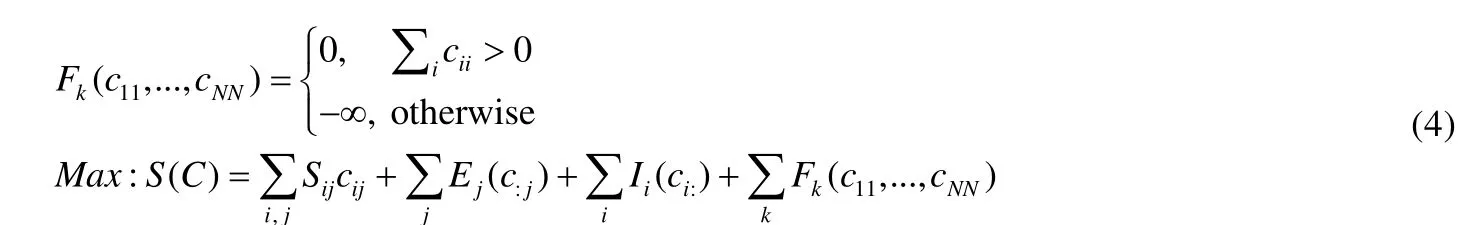
依据max-sum 算法,可以从新的全局函数及信息传递过程中[17,20]推导出如下公式:
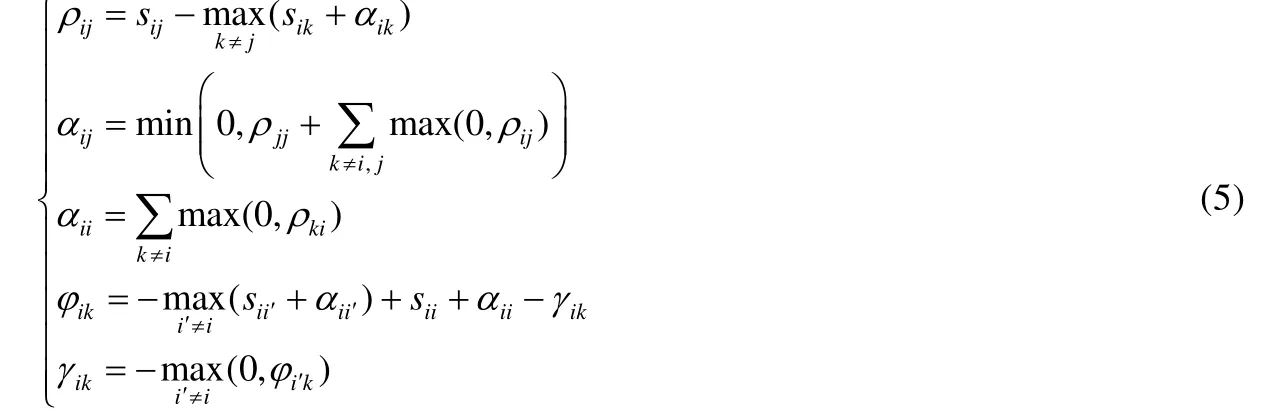
与公式(2)比较可以发现,新增信息量γik和φik不影响原本吸引度和归属度的更新过程.因此,引入额外信息改变pk不会改变AP 算法的核心公式.
轮廓系数是确定聚类质量的一种常用指标,通常用来评价整体聚类质量的好坏,但也可以用来评估某一个样本点簇归属的合适程度.假设数据集被划分为x个子集{C1,C2,…,Cx},a(i)是子集Ck中的样本点i到同簇其他样本点间的平均相似度,b(i,Cj)(i≠j)是样本点i到子集Cj中所有样本点的平均相似度.b(i,:)=min{b(i,Cj)}.一个样本点的簇归属合适程度计算方法如下:

Silhouette(i)的取值范围为[-1,1]:越接近1,则样本点i的簇归属越合理;接近-1,说明样本点i应属于其他簇;为0,则说明样本点i在两个簇的边界上.
在AP 算法迭代产生聚类中心的情况下,引入对样本点的轮廓系数评价.参考Silhouette指标的结果可以得知样本点是否被正确地划分,以及被选作聚类中心的样本点是否是正确的聚类中心,从而调整每个样本的偏向参数{pk},动态改变样本点成为聚类中心的可能性.显然,聚类中心样本与非聚类中心样本在调整上存在差异,因此给出两条偏向参数更新规则.
规则1.对于非聚类中心样本:Silhouette指标大于0,说明该样本被划分到正确的簇,其成为聚类中心的可能性应该降低,pk应适当减小;Silhouette指标小于0,则该点没有被划分到正确的簇,其应该被划分到其他簇或成为一个新的聚类中心,pk应维持不变或适当增加.
规则2.对于聚类中心样本:Silhouette指标大于0,说明该样本是正确的聚类中心,pk应维持不变或适当增加;Silhouette指标小于0,说明该点不是正确的聚类中心,pk应适当减小.
基于上述两条规则,为了将Silhouette转化为合适的Δp,定义如下转换函数:

O={ok}1×N存放聚类中心标志,如果ok=1,表明样本点i是聚类中心;否则,ok=-1.参数δ调整Δp的变动幅度.引入基于Silhouette计算的Δp,当算法产生至少一个聚类中心后,偏向参数动态赋权的AP 算法更新公式如下:
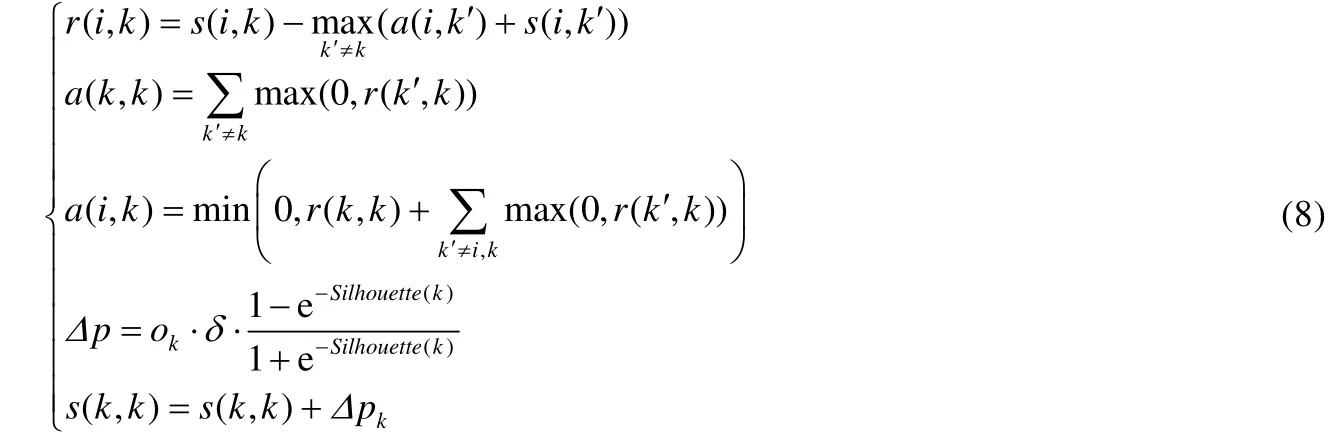
偏向参数动态调整的AP 算法在复杂度上与标准AP 算法没有差别,但是因为考虑到了样本点之间的相互作用关系,使得偏向参数能够即时反映样本点当前迭代时刻的状态.对于基于聚类划分的采样问题来说,期望得到的代表点能够更大程度地覆盖原始数据的空间区域,包含更多数据密度较小区域的特异性样本,而引入偏向参数的动态调整能够在一定程度上消除原始数据密度分布给初始偏向参数带来的影响,从而能够找到更多低数据密度空间区域中的代表性样本.引入轮廓系数动态改变偏向参数后,算法过程如下.
算法1.adjustPreferenceAP(S,P,λ,δ,maxiter,conviter).
输入:数据集相似度矩阵S={sij}N×N,偏向参数P={p11,...,pNN},阻尼系数λ,变动幅度δ,最大迭代次数maxiter,最大收敛状态比较次数conviter;
输出:聚类中心classcenter.


3 分层增量采样
AP 算法中,聚类中心为真实样本点这一特性,使得其非常适用于代表点的采样.但是标准AP 算法的复杂度较高,不适用于大规模数据的代表点采样.本文结合分层及增量处理的采样策略,基于上述偏向参数的动态赋权AP 算法,实现对数据集的高效采样,以期实现处理效率和采样质量的更好兼顾.
本文提出的分层增量采样方法框架如图1 所示,是一层增量局部推选加一层合并推选的“1+1”模式的采样.算法的输入为已划分好的子集序列,为了保证算法的计算效率,各子集的规模要相同或相近,可以采用顺序划分或随机采样划分的方法.
将数据集划分为规模适中的子集{D1,D2,…,Dn},分层增量采样的第1 层(增量局部推选)依次处理样本子集Di,选出基于全局偏向参数信息和局部相似度信息的子集代表点Ri={ri1,ri2,…,rix},构成子集代表点集R.第2 层 (合并推选)完全基于R的全局信息,即数据集的局部信息,从R中挑选出数据集的整体代表点.
在增量局部推选层中,为了将更多的潜在代表点挑选出来,需要考虑数据集的全局相似度信息.因此,将样本点基于整个数据集中的全局初始偏向参考度作为AP 算法的输入.依据公式(1)计算数据集的全局偏向参数PG={pgkk},每个子集的全局偏向参数集合为PGi.
合并推选层采样是对增量局部推选层采样结果的合并推选.在第1 层中已经基于全局偏向参数获得了所有潜在的整体代表点组成局部代表点集,在第2 层采样中,只需基于局部代表点集的全部相似度信息,即整体数据集的局部节点之间的相似度信息进行潜在代表点的采样选择,其中,仍采用公式(1)初始化其中局部代表点集相对于整体数据集的局部偏向参数PN={pnkk}.
结合截断值参数θ的引入,本文方法可考虑对原始的所有数据点间的相似度矩阵进行约简,将小于相似度截断值的边进行删除,进而达到约简相似度矩阵的目的,加速AP 算法的计算效率.综前所述,可归纳给出如下的综合算法过程.
算法2.ISAP({D1,D2,…,Dn},θ,λ,δ,maxiter,conviter).
输入:子集序列D1,D2,…,Dn,相似度截断值θ,阻尼系数λ,变动幅度δ,最大迭代次数maxiter,最大收敛状态比较次数conviter;
输出:代表点集R′,全局划分Cluster.

选出数据集的整体代表点后,如果需要实现单簇多代表点的选择,则可依据最大相似度将非代表点分配给一个代表点,完成基于最大相似度分配的全局簇划分.然后依据最终的簇划分,在每个簇中选取一组点放入代表点集.
4 算法分析
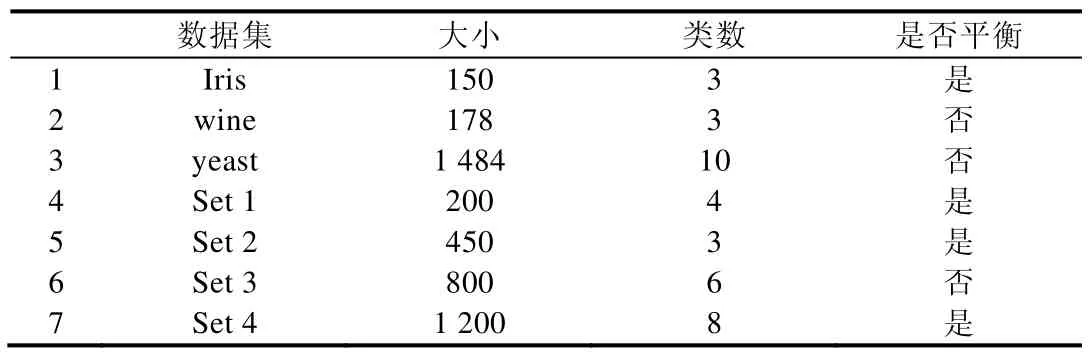
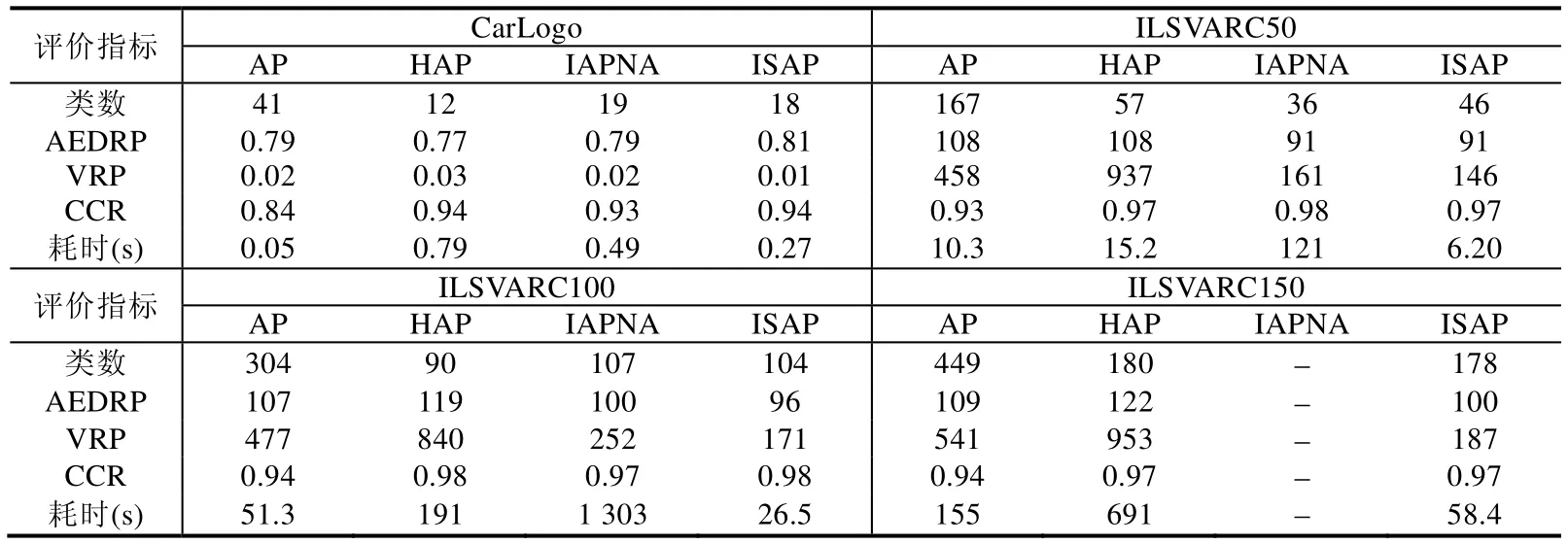
假设数据集被划分为K个规模为M的子集(K< 在各子集上执行AP 算法的空间复杂度为O(M2),每一次增量推选过程中消耗的存储空间不变,因此增量执行K次规模为M的AP 算法的空间消耗为s1=O(M2).依照上述设定,在局部代表点数为ρ·K·M的情况下,在局部代表点集上执行AP 算法的空间消耗为s2=O(ρ2K2M2),因此分层采样方法的空间复杂度为O(ρ2K2M2).而标准AP算法的空间复杂度为O(K2M2).ρ是一个大于0 且远小于1 的数,因此分层增量采样方法在空间上的消耗同样优于标准AP 算法.分层增量采样方法在时间效率和存储空间方面均可以得到提升. 相比于标准的AP 算法,ISAP 中引入了大规模数据的分层处理策略,在第1 层处理中对原始数据进行一次局部约简处理后,仅选取部分代表性数据参与第2 层的再处理,从理论上看,可能会造成代表性数据对原始数据信息携带不足的问题,进而导致最终采样得到的代表性样本在全局上的偏离问题.虽然如此,结合我们以前的相关研究[21,22]发现:在增量学习过程中,如果阶段性选择的代表点集能够构成对目标问题解的一个整体有效的表达,那么在增量过程中逐步筛选掉非代表性样本,仅基于保留下来的数据参与后续处理的做法,理论上在一定条件下可以达到与全局方法的一致. 具体到ISAP 算法,考虑在第1 层处理后保留的局部代表性样本集是在整体上对原始数据空间区域进行代表性表达,而非数据密度上的约简采样.这样,AP 算法自身的特性就显得非常有优势,不仅可以有效地约简冗余数据,减少计算量,而且能够一定程度上解决原始数据空间中局部数据密度可能存在较大程度不平衡的问题,以使得最终得到的采样结果更优. 本文提出的代表点采样方法基于AP 聚类,为检验算法有效性,同样与基于AP 的其他聚类方法进行比较,几种比较方法如下. (1) 标准AP 算法的代表点采样:使用文献[12]提出的标准AP 算法来做代表点选取; (2) 分层近邻传播算法HAP 的代表点采样:使用文献[23]提出的一种基于底层推举和上层推举的层次AP算法来做代表点选取.该方法同样采用分层的策略,底层基于标准AP 算法,上层基于自适应AP 算法; (3) 近邻赋值的增量式AP 聚类算法IAPNA 的代表点采样:使用文献[16]提出的一种增量式AP 算法来做代表点选取.该方法通过近邻赋值构建新增数据与已有数据之间的消息传递关系,增量式地扩充吸引度和归属度矩阵,直至方法收敛得到结果. 相关算法实验中,首先需要计算样本点i和j之间的相似度s(i,j),s(i,j)的值越大,表示两个样本越相近.实验中,对两个样本点间的相似度s(i,j)采用归一化计算定义: D={d(i,j)}是样本点之间的欧式距离矩阵,max 和min 操作分别表示取矩阵元素中的最大值和最小值.上式计算后,两个样本点完全相同时的相似度为1,完全不同时的相似度为0. 实验中,参考各自算法特点和相关文献,AP 算法的偏向参数取相似度矩阵中位值;对于IAPNA 方法参数pc,根据算法输出簇数和采样质量选取对比选取;对于ISAP 算法中的截断参数θ和变动幅度参数δ,一方面也可类似地根据算法输出簇数和采样质量选取对比选取,其中的采样质量可以是使用有监督的交叉验证选取;或者使用无监督的质量指标(如代表点间平均欧式距离)作为参照. 此外,截断参数θ一定程度上反映了数据点间距离度量合理性的界限范围,而变动幅度参数δ是从微观上对偏向参数进行调整,解释样本点对于轮廓系数的学习能力.由此,取θ选择范围可取[10-2,max(D)],δ选择范围可设定为[10-3,10-1],其中,max(D)同公式(9)中的含义. 实验从聚类质量、采样质量和方法效率这3 个方面对代表点采样方法进行评价.标准化互信息(normalized mutual information,简称NMI)是广泛用于聚类质量评估的聚类评价指标,用于度量方法结果与标准结果之间的相似度,其定义如下: 其中,N是数据样本总数;CX和CY分别是数据集的真实划分和算法聚类结果包含的簇数;Cij表示同时属于真实划分簇数i和聚类结果簇数j的样本数量.NMI的取值范围为[0,1],其值越大,表示聚类结果与真实结果越匹配. 针对采样质量,本文引入代表点间平均欧式距离(average euclidean distance of representative points,简称AEDRP)和距离方差(variance of representative points,简称VRP)以及新设计综合覆盖率(comprehensive coverage rate,简称CCR)来评价选取代表点的显著性和覆盖性.代表点间平均欧式距离越大,距离方差越小,说明选取的代表点的显著性越好.综合覆盖率考虑反映在合理代表点个数下,代表点集对原始数据集的覆盖程度.值越大,说明选取的代表点的覆盖性越好.其定义如下: 其中,NR是算法划分的类数即代表点数目,NNR是非代表点数,R和NR分别为代表点集和非代表点集;dist(i,j)是代表点i和非代表点j间的欧式距离,dist(:,j)min是非代表点j与所有代表点之间的最小距离;dmean是整个数据集中数据点间的平均欧式距离;I(·)为指示函数.CCR值综合考虑代表点占原始数据大小的比例以及代表点对数据集在一定范围内的覆盖程度,通常情况下,选取更多数量的代表点能够明显提升代表点对数据集的覆盖程度.因此,在不考虑选取代表点数量的情况下去比较代表点对数据集的覆盖程度是不合理的,所以在评价时引入与代表点数目相关的系数,可以更为合理地评价代表点对数据集的覆盖程度.当然,在采样问题中,覆盖度是更被看重的问题,因此在CCR评价指标中,代表点数目的影响权重较小,代表点对数据集覆盖程度的影响权重较大. 在3 组UCI 标准数据集和4 组人工合成数据集上进行代表性样本采样实验,数据集详情见表2. Table 2 Descriptions of numerical experimental data sets表2 数值型实验数据集描述 真实数据集iris,wine,yeast 来源于UCI,人工合成数据集Set 1~Set 4 是随机生成的二维数据集,均符合正态分布,其样本分布情况如图3 所示.对每个数据集,依据公式(9)计算任意数据集内样本点间的相似度.4 种算法的AP 阻尼系数λ设为0.9,HAP 算法和ISAP 算法的分区子集大小设为数据规模的0.2[23],如果子集规模超过500,则设为500.采样选取每个最终簇的一组数据(算法输出的代表点)作为代表点. 在实验过程中,调整IAPNA 算法参数pc、ISAP 算法截断参数θ和变动幅度参数δ进行多次实验.参数pc在真实数据集上的数值来源于文献[16],参数θ,δ以及人工数据集上的pc综合算法输出的簇数和采样质量选取.最终实验参数设置见表3. Fig.3 Four synthetic data sets图3 人工合成数据集情况 Table 3 Parameter setting for numerical experimental data sets表3 数值型数据实验算法参数设置情况 相应的实验结果见表4、表5.从表中结果可以看到:AP 算法在小规模数据上耗时最短,但随着数据规模增加其效率大幅下降,并且在所有数据集上的聚类质量和采样质量都不太理想;IAPNA 算法是增量式输入数据的全局AP 算法,其聚类质量和采样质量最优;但随着数据规模扩大,其时间消耗剧增,不适用于大规模数据的代表点采样;HAP 算法与ISAP 算法都是分层采样代表点的方法,两种方法的聚类质量和采样质量均优于AP 算法,接近IAPNA 算法,但两种算法耗费的时间远低于IAPNA 算法.但是HAP 算法在合并推选层上采用的是自适应AP 聚类算法,需要执行多次标准AP 算法得到最优的结果;随着数据规模的扩大,参与合并推选层采样的数据量也随之增大.因此,HAP 算法的时间消耗增加幅度比ISAP 算法要大.ISAP 算法在聚类质量和采样质量与IAPNA,HAP 算法处于相同水平,但计算消耗的时间显著较短. 上述实验结果也从实际应用角度表明:引入改进AP 算法过程和分层处理的ISAP 算法不仅获得了比标准AP 算法更好的采样效果,且可以具有更好的计算效率.这也在一定程度上佐证了前文第4 节中关于ISAP 算法性能的理论分析结果. 4 种算法在yeast 数据集上的效果都不理想.wine,yeast 和Set 3 数据集内各簇的规模不尽相同,但是wine 和Set 3 各簇之间规模相似,而yeast 的簇规模差别较大,是典型的不平衡数据.从实验结果看,几种对比算法在不平衡数据集的效果均相对较差. 对于代表点综合覆盖率性能指标,其与代表点对数据集的覆盖度和簇数(代表点数)有关,一般簇数越大,选取的代表点越多,其代表点对数据集的覆盖度越大.从UCI 标准数据集上的结果来看:相比于标准AP 算法,ISAP算法能在产生更少代表点的同时获得较大的代表点覆盖度,因此其综合覆盖度较高.此外,从人工合成数据集上的结果来看:ISAP 算法在与HAP,IAPNA 算法产生相同簇数的情况下,ISAP 算法产生的代表点间的平均距离较大,方差较小,说明代表点间的相似性低,挑选结果平滑,显著性较好. Table 4 Performance results obtained by several compared sampling methods on three UCI datasets表4 不同方法在3 个UCI 数据集上的性能对比结果 Table 5 Performance results obtained by several compared sampling methods on four synthetic datasets表5 不同方法在4 个人工数据集上的性能对比结果 在本实验中,实验图像集来自搜索得到的车标图像以及ILSVRC2014 图像集.车标图像集Carlogo 共有270张图像,包含18 个类别的车标,每类包含15 幅图像.分别取ILSVARC2014 验证集的前50 类、前100 类和前150类构成图像数据集ILSVARC50,ILSVARC100,ILSVARC150,分别包含2 500、5 000 和7 500 张图像. 实验过程中,调整IAPNA 算法参数pc、ISAP 算法截断参数θ和变动幅度参数δ多次执行算法,综合算法输出的簇数和采样质量选取,最终实验参数设置见表6.代表性图像选择实验仅评估算法的采样质量.其中,Carlogo图像集采用SIFT 特征匹配度作为图像间相似度,SIFT 相似度经过公式(9)转换后得出Carlogo 数据集上的AEDRP指标.ILSVARC 图像数据集则使用卷积神经网络(convolutional neural networks,简称CNN)提取图像的特征向量,依据公式(9)计算图像间的特征相似度. Table 6 Parameter setting in representational image selection experiment表6 代表性图像选择实验参数设置情况 实验结果见表7.从表中结果可以看到:综合考虑代表性图像的平均距离、距离方差、综合覆盖度以及时间效率,ISAP 算法具有较为明显的优势.标准AP 算法在各方面都不占优势;IAPNA 方法在数据集规模较大时时间耗费过大;而HAP 算法得到的代表图像之间的平均距离较大,但是代表图像间距离的方差明显超过另外3 种方法,其代表图像间的距离分布不平滑. Table 7 Performance results obtained by serval compared methods on representational image selection problem表7 对比方法在代表性图像选择实验上的性能结果 ISAP 算法从数据集CarLogo 中选择的代表性图像如图4 所示. Fig.4 Representational images selected by ISAP on CarLogo data set图4 ISAP 在CarLogo 数据集上挑选的代表性图像 可以看到:通过本文方法得到的代表性图像很好地覆盖了数据集,能够作为数据集的代表. 深度学习是数据驱动的方法,用规模更大、质量更好的数据集去训练神经网络一般都能够得到泛化性能更好的模型.但在实际情况中,数据的采集面临多重困难,人工采集的样本在多样性和规模上均不能满足实际训练的需求.数据增强即数据扩增,是一种有效扩充数据规模,解决训练样本不足问题的方法[24-26].数据增强能够扩充数据规模,增加数据噪声,使用增强后的数据集训练神经网络能够提高模型的泛化能力和鲁棒性.在图像识别领域,数据增强可以很好地提升训练模型的识别率.但简单的数据增强策略容易产生许多极其相似的图像序列. 考虑检验ISAP 算法在数据增强任务上的价值,实验数据来源于加州理工大学开源数据集leaves,包含3 种类型的叶片,共186 张图像.利用仿射变换、高斯噪声、区域衰减、高斯模糊等数据增强手段,将leaves 数据集的规模扩充10 倍至1 860 张图像,命名为leavesDa10.在leavesDa10 的基础上,再次利用上述数据增强手段将数据集规模扩充5 倍至9 300 张图像,命名为leavesDa50. 在leavesDa50 上执行参数不同的ISAP 算法,采样选取每个最终簇的10 幅图像(ISAP 算法输出的代表点及每个簇中离代表点最近的另外9 幅图像,规模不足10 的簇则选取其全部图像)作为代表图像,并考虑形成约 1 860 张增强样本图像为目标,最终生成增强数据集leavesDaIsap0~leavesDaIsap4.leaves 叶片类型与部分增强图像如图5 所示. Fig.5 leaves blade type and partial enhanced images图5 leaves 叶片类型与部分增强图像 在各数据集上,从每类叶片中取3/4 的图像用于卷积神经网络CNN 训练,其余1/4 的图像用于模型测试,使用参数不同的ISAP 算法产生的约简数据集训练得到的模型平均识别率(10 次实验结果的平均)如表8 所示.其中,采样指标AEDRP 值依据算法直接输出的代表点进行计算. Table 8 Performance results obtained by different ISAP-augmented deep learning on leaves recognition task表8 不同参数ISAP 算法数据增强下leaves 叶片识别问题的深度学习性能结果比较 考虑以采样比例和AEDRP 指标为依据,针对表8 中的实验结果,将leavesDaIsap0 数据集上训练的结果与其他方法进行比较. 考虑在leavesDa50 上执行HAP 算法,用上述选取代表性图像方法构成增强数据集leavesDaHap;为了更好地与HAP 算法进行对比分析,调整ISAP 参数为θ=0.3,δ=0.05,可形成规模为4 584 的数据集leavesDaIsap5,相应的实验结果见表9,其中的平均识别率为10 次实验的平均结果. Table 9 Performance results obtained by different augmented datasets on leaves recognition task表9 不同增强数据集下leaves 叶片识别问题的深度学习性能结果比较 从表9 中实验结果可以看到:leavesDa10 与leavesDaIsap0 的规模相近,在经过ISAP 算法采样约简的数据集leavesDaIsap0 上训练学得的模型识别率远好于在使用简单数据增强手段的leavesDa10 上训练学得的模型识别率.leavesDa50 是基本数据增强扩充50 倍后的数据集,其规模大致是leavesDaIsap0 的5 倍.用leavesDaIsap0 训练得到的模型的识别率与用leavesDa50 训练得到的模型的识别率相差已不大.在经过HAP 算法采样约简的数据集leavesDaHap 上训练得到的模型识别率接近在leavesDa50 上学得的模型,其数据规模只有leavesDa50 的1/2 左右.但是相比于ISAP 算法的采样,HAP 算法的采样并不占优势.因为HAP 算法无法有效获得可控数量的代表点集,ISAP 算法在调整参数的情况下可以控制输出代表点的规模.而在最终样本规模相近的情况下,ISAP算法数据增强策略相对于HAP 算法数据增强策略获得的模型识别率也较为接近.而在实际使用时,由于ISAP算法计算效率显著较高,显然具有更高的实用价值. 综上表明,数据增强手段结合进高效增量采样处理后,在不改变总训练数据集规模的情况下,ISAP 算法介入所获得的模型质量可实现显著的提升.且ISAP 算法能够控制约简后数据集的规模,有效地在减小数据规模的同时,保证数据集的多样性;在保持数据集规模不变的情况下有效提升数据质量,增加样本多样性.此外,因为ISAP 高效的处理速度,可以快速地处理更大规模的数据增强数据集,更好地满足现实应用需求. 本文针对数据集代表点采样的一般性问题,提出了一种基于动态赋权近邻传播的数据增量采样算法ISAP.算法通过引入分层增量处理和样本点动态赋权策略,结合偏向参数动态赋权的AP 算法,有效地实现了处理效率和采样质量的兼顾,更好地满足大规模数据集上的高效代表点选择.设计实验分别使用人工数据集、UCI 标准数据集和图像数据集进行性能分析,与其他方法相比,ISAP 算法在获得了采样划分质量与其他方法处于同一水平的同时,计算效率获得了大幅提升.进一步将ISAP 算法应用于深度学习的数据增量任务中,相应实验结果表明:基本数据增强策略结合进高效处理的ISAP 算法后,在不改变总训练数据集规模的情况下增加了样本的多样性,在保留样本多样性的同时约简了训练数据集的规模,新数据增强后所获得的模型质量可实现显著的提升. 在下一阶段,我们将从以下几个方面进行尝试. (1) 本文中使用的数据规模与实际情况可能会面临的数据规模相比,规模还不够大.当数据规模扩大到一层增量局部推选加一层合并推选的“1+1”模式的采样无法处理时,研究如何将该方法扩充至n层增量局部推选加一层最终合并推选的“n+1”模式的采样; (2) 类似于标准的AP 算法,本文方法还不能很好地适应于类规模差别较大的数据集,在不平衡数据集上的采样效果不太理想.对算法过程作何改进,能够使其适用于不平衡数据集,是一个值得思考的问题; (3) 作为一种同步约简的增量式采样算法,关于其中理论性能的分析研究还不够深入,这也将在我们的后续研究中进一步展开.5 实验分析

5.1 评价指标
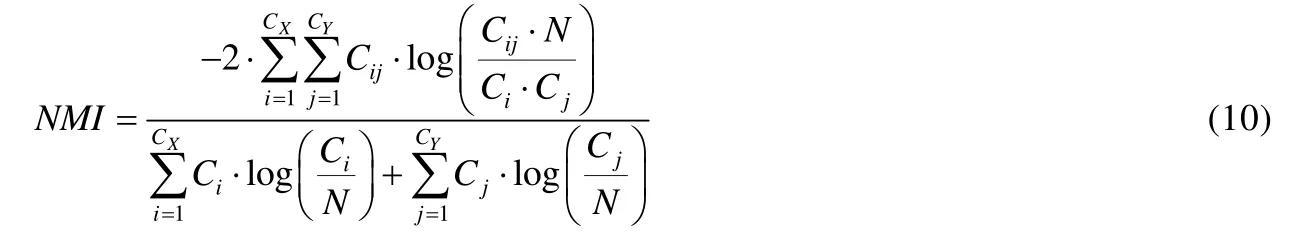
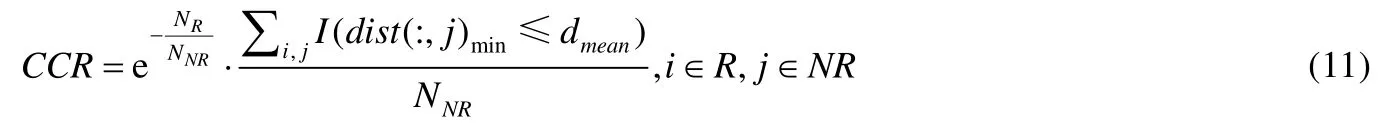
5.2 数值数据实验分析




5.3 代表性图像选择


5.4 数据增强应用



6 结论与展望

