面向多目标优化的多样性代理辅助进化算法*
孙哲人,黄玉划,陈志远
(南京航空航天大学 计算机科学与技术学院,江苏 南京 211106)
多目标优化问题(multi-objective optimization problem,简称MOP)[1]是指包含两个或两个以上目标的优化问题,其目标之间往往相互冲突且难以相互比较.由于能够较好地权衡多目标优化问题中的多个目标,进化算法逐渐成为了很多领域中解决多目标优化问题的一种较为流行的工具[2],如经济、金融、工程[3-5].
在过去的30 多年里,专家学者对多目标进化算法进行了大量的研究,提出了许多先进的算法,大体可以分成基于支配、基于分解和基于指标这3 种[6]:基于支配的算法主要有Zitzler 等人提出的SPEA2[7]和Deb 等人提出的NSGA-II[8],基于分解的算法主要有Deb 等人提出的NSGA-III[9]和Zhang 等人提出的MOEA/D[10],基于指标的算法主要有Zitzler 等人提出的IBEA[11]和Beume 等人提出的SMS-EMOA[12].进化算法在解决多目标优化问题时,需要对解进行大量的真实评估,即,使用原始的目标函数评估解.然而,现实中存在很多问题需要计算机仿真、真实实验或数据驱动的方式来评估,因此其评估过程往往需要花费大量时间、人力、物力和财力,这类问题被称为昂贵问题[13],如创伤系统优化[14]等.对于昂贵问题,由于受到评估时间的限制,进化算法难以在短时间内给出较好的结果.而代理辅助进化算法可以通过廉价的模型评估代替昂贵的真实评估来加速进化算法,大大减少评估过程的代价,同时能够保证较好的优化结果.
目前,常用的代理模型主要有多项式响应模型、Kriging 模型、神经网络模型、径向基函数网络模型和支持向量回归模型,但在选择代理模型方面缺乏理论指导[2].一般来说,在使用插值法的模型中,首选的是Kriging模型,因为Kriging 模型在评估解的目标值的同时,可以给出解的不确定性,而不需要额外使用其他方法来计算不确定性.因为有此特性,Kriging 模型是代理辅助进化算法一个较为流行的选择,如Knowles 提出的ParEGO[15],Ponweiser 等人提出的SMS-EGO[16],Zhang 等人提出的MOEA/D-EGO[17]和Chugh 等人提出的K-RVEA[18]都使用了Kriging 模型.
以上提到的算法是此领域较为流行且具有代表性的算法,它们选择解的时候更多关注解在模型评估下的收敛性.但很多情况下,在模型评估下的好解是伪好解,即在真实评估下并不是好解.对于Kriging 模型来说,训练样本的分布对模型评估的准确度有很大的影响,训练样本在需要评估的解四周分布越广泛,则模型评估会相对越准确[19].对于多目标优化问题,广泛分布在帕累托前沿(Pareto front,简称PF)上的解,也会较为广泛分布在帕累托最优集合(Pareto set,简称PS)上[20].因此,如果能够在真实PF 附近得到分布较为广泛的样本,Kriging 模型就可以较好地近似真实PF 附近的局部空间,从而增加找到在真实PF 附近的解的可能.这就需要更多地考虑多样性,而不只是收敛性.因此,本文提出了基于多样性的代理辅助进化算法(DSAEA)来解决昂贵多目标优化问题.
1 背景知识
1.1 多目标优化问题
多目标优化问题的一般形式如下:

其中,F(x)={f1(x),...,fm(x)}T为m个目标组成的目标向量,x={x1,...,xd}T为d个决策变量组成的决策向量,Rd为d维决策空间,Rm为m维目标空间,F 表示从决策空间映射到目标空间.当且仅当∀i={1,...,m},fi(xk)≤fi(xl)和∃j={1,...,m},fj(xk)<fj(xl),则称xk支配xl.如果一个解在解集中没有解能够支配它,则称为非支配解;反之,则称为支配解.所有非支配解的决策向量构成的集合叫做帕累托最优集合PS,对应的目标向量构成的集合叫做帕累托前沿PF.
1.2 代理辅助进化算法
代理辅助进化算法中的评估方式分为两种.
• 一种为真实评估,即用原昂贵问题进行评估,正如引言部分提到的,用原昂贵问题进行评估一般需要仿真计算、真实实验、数据驱动的方式,需要巨大的代价.因此,真实评估需要被限制使用,不然优化时间会是难以接受的;
• 另一种为模型评估,即用训练的代理模型进行评估,这种方式相比真实评估只需要非常少的消耗.
本文所涉及到的代理辅助进化算法流程如图1 所示,更多有关代理辅助进化算法的内容可以查阅文献[2,13].图1 中,初始化是在决策空间内随机采样一定数量的解,并进行真实评估.这些解作为训练集,用于建立代理模型.候选解生成算子是在模型评估下迭代优化产生候选解.选择算子是在候选解中选择部分候选解进行真实评估,并加入到训练集以更新代理模型.此时,若未达到真实评估上限,则继续迭代优化;否则输出真实评估过的解,即种群中的非支配解.其中,与一般进化算法的选择过程不同的是:由于受到真实评估次数的限制,同时,模型评估与真实评估的函数值存在一定的误差,代理辅助进化算法需要选择更具代表性的解[17].即:在现有种群中对候选解的收敛性与多样性进行权衡,而不是直接按照适应度值进行选择.另外,新候选解的产生并不是把当前种群直接作为父代解,同时,真实评估的解较少,因此在代理辅助进化算法中,种群并没有明显的迭代更新过程,而是用于保存所有真实评估过的解.
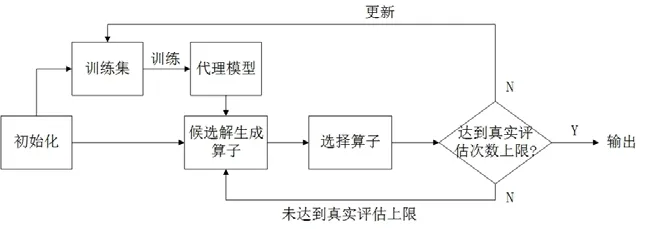
Fig.1 Flow diagram of the SAEA图1 代理辅助进化算法流程示意图
1.3 相关工作
目前有较多研究针对解决多目标昂贵问题的代理辅助进化算法,这里简要介绍较为流行的算法.
• Knowles 提出的ParEGO[15]拓展了EGO[19],并首次把EGO 用于解决多目标优化问题.ParEGO 把问题均匀划分成多个子问题,即把多目标优化问题转化为单目标优化问题,每次随机选取一个子问题,把预期改善(EI)[19]作为选择策略来选择进行真实评估的解.此外,ParEGO 还限制了训练集的大小以减少建模时间;
• Ponweiser 等人提出的SMS-EGO[16]使用下置信界(LCB)[21]来划分解的支配关系,把得到的解分成非ε支配解、ε支配解、支配解:对于非ε支配解,SMS-EGO 计算其S-metric作为适应度;对于ε支配解和支配解,SMS-EGO 分配一个惩罚值作为适应度,距离非支配解越远惩罚越大.基于此选择策略来选择进行真实评估的解.虽然SMS-EGO 表现不错,但是由于需要大量计算S-metric,所以它的运行时间特别长;
• Zhang 等人提出的MOEA/D-EGO[17]先对进化算法得到解聚类,然后把EI 作为选择策略,在每一簇中选择一个解进行真实评估.此外,它采用模糊聚类的方法建立代理模型,在利用所有真实评估的解的同时减少了建模时间.与ParEGO 相比,MOEA/D-EGO 运行速度相对更快,因为它每次批量选择解,而不只是选择单个解;
• Chugh 等人提出的K-RVEA[18]更多的贡献在模型管理策略上.它把本次得到的候选解与上一次得到的候选解分别分配到一组参考向量上:如果不活跃的参考向量在数量上的变化少于一定的数量,就采用不确定性作为选解依据;否则采用角度惩罚距离作为选解依据.此外,K-RVEA 在更新模型的时候会筛选解来限制训练集的大小,从而减少建模时间;
• Pan 等人提出的CSEA[22]采用前馈神经网络(FNNs)模型作为代理模型,其作用不同于以上几个算法,这里代理模型是作为分类器使用.迭代开始时,它把真实评估的解按比例分成训练集和测试集,并计算出分类器在测试集上非支配解和支配解的错误率.在选择过程中,分类器把进化算法得到的解分成非支配解和支配解两类;同时,根据分类器在测试集上的错误率与阈值对比来确定是选择非支配解还是选择支配解进行真实评估.
2 基于多样性的代理辅助进化算法(DSAEA)
DSAEA 算法框架如算法1 所示.
• 步骤1、步骤2 是初始化部分,该部分先在目标空间内均匀生成参考向量,再随机采样初始解,并在真实评估后加入种群P和训练集A;
• 步骤3~步骤10 是算法的主要迭代过程,在真实评估次数达到上限后,算法便会终止并输出最终解,即种群P中的非支配解.其中:步骤4 是用训练集A来训练代理模型;步骤5 是候选解生成算子,它会在模型评估下迭代优化候选解,如算法3;步骤6 是选择算子,它是根据选择策略选择μ个候选解进行真实评估,如算法4、算法5;步骤8 是训练集更新,如算法6.训练集A会在每一次迭代后进行更新,以保证下一次迭代时训练出的模型有较好的精度.
算法1.DSAEA 算法框架.

DSAEA 主要由初始化、代理模型构建、最小相关解集计算、候选解生成算子、选择算子、训练集更新这6 个部分组成,下面分别进行详细说明.
2.1 初始化
初始化部分主要包括均匀生成参考向量和生成初始解.
(1) 均匀生成参考向量:利用正则单形点阵设计方法[23,24]在单位超平面上生成一组均匀分布的参考向量.对于每个参考向量,从下面集合中均匀取值:

且满足:

其中,H用于控制参考向量生成的间隔,m为目标数量.生成参考向量的数量为;
(2) 生成初始解:利用拉丁超立方随机采样(LHS)[25]方法对决策空间均匀采样初始解.如文献[15,17,18]所述,较为合适的随机采样次数为11d-1,其中,d为决策变量的数量.
2.2 代理模型构建
本文采用Kriging 模型作为代理模型,即高斯过程来拟合目标函数,分别对每一个目标建模.一方面,Kriging模型在评估目标值的同时可以给出该目标上的不确定性,不需要使用额外的方法评估解的不确定性;另一方面,Kriging 模型因其有效性而较为流行,很多研究都使用它,方便对比.下面对训练Kriging 模型做一个简要说明,更多细节见文献[19,26].
为了建立一个廉价的Kriging 模型,我们需要两点假设.
• 第一,假设对于任意x,其目标函数值y都满足:

其中,μ是回归模型的预测值,ε~N(0,σ2);
• 第二,假设对于任意两个xi和xj,它们的高斯随机过程的协方差与它们的之间的距离相关,表示如下:

其中,θk和pk为超参数,pk∈[1,2].
在以上假设的基础上,对于NI个训练样本,我们可以最大似然,公式(4),来估计参数μ和σ2:

其中,y为训练样本的目标函数值,1 为长度为NI的单位列向量,det(R)为相关矩阵R 的行列式.R 表示如下:

为了最大化公式(4),可以得到μ和σ2:


其中,rT是样本与输入的相关矩阵:

2.3 最小相关解集计算
因为候选解生成算子、选择算子和训练集更新都需要计算最小相关解集,算法2 用于算法3、算法5 和算法6 中,所以这里优先对其进行介绍.
把原问题分解为多个单目标子问题来求解,可以较好地权衡解的收敛性和多样性[8,9].这里的计算最小相关解集也是基于分解的思想,它引入参考向量把原问题分解为多个单目标子问题,再求得每一个子问题最小相关解.所有参考向量的最小相关解组成的集合即为最小相关解集.其中的每一个最小相关解对应一个子问题的当前最优解,因而最小相关解集的大小与解的多样性有关.最小相关解集越大,则越多的子问题存在当前最优解,即这个集合的多样性越好;反之亦然.
DSAEA 是按照解与参考向量的角度来判定它们的相关性的,并在此基础上得到参考向量的最小相关解.
解x 与参考向量w 的角度θ的计算如下:

最小相关解集的具体算法见算法2,其中,d(x,z*)为解x 到理想点z*的距离.对于解集X中的每个解x,其相关参考向量是与x 相差角度最小的参考向量.对于一个参考向量w,其相关解为所有相关参考向量为w 的解,可能没有也可能很多个.参考向量w 的最小相关解为w 的相关解中距离理想点z*最近的一个.所有参考向量的最小相关解组成的集合即为解集X的最小相关解集.其中,z*=(min(f1),...,min(fm)),min(fi)为种群P中的解在第i个目标上的最小值.
算法2.最小相关解集MCS.

2.4 候选解生成算子
候选解生成算子是在模型评估下迭代优化候选解,以得到在现有模型下表现较为优秀的候选解,具体见算法3.为了充分利用现有条件,候选解生成算子使用训练集A作为初始解,而不是重新随机采样.每次生成子代解之前,如果|X|小于|A|,就从训练集A中随机选择|A|-|X|个解加入X.这样可以使X中解的数量不会太少,以提高算法的探索能力和解的多样性,从而更大机会搜索到更多有希望的候选解.在得到初始父代解后,候选解生成算子使用模拟二进制交叉(simulated binary crossover)[27]和多项式突变(polynomial mutation)[28]算子生成子代解,并使用Kriging 模型评估其函数值.然后计算父代解和子代解并集的最小相关解集,把最小相关解集中的解作为下一代父代解继续迭代优化.当达到最大迭代次数时,输出候选解集.
算法3.候选解生成算子Candidates.


2.5 选择算子
选择算子是在候选解集中选择部分解进行真实评估,具体见算法4.其先是找到每个解x∈X的邻居参考向量,然后根据是否存在活跃的邻居参考向量,把x 加入Xa或Xia.这里的活跃与否是看该参考向量在种群P中是否有相关解,即该子问题上是否存在已经真实评估的解.接下来,算法对Xa和Xia进行筛选,删除一些希望渺茫的解,见算法5.然后,对解集X使用Kmeans 方法聚类,划分成μ个簇,并在每个簇中选择一个与理想点z*距离最小的解.与文献[17,18]中所说明的一致,在本文实验中,μ设置为5.
算法4.选择算子Selection.

算法5.筛选.

由于模型评估具有一定的误差,真实评估的函数值相对模型评估的函数值会发生一定程度的偏移.这里,我们根据解的不确定性来确定其邻居参考向量.算法4 中的阈值θth的计算如公式(12):

公式(13)中的p是一个系数,本文实验取是所有目标上不确定性组成的向量,其中,f1对应的不确定性取负.
对Xa或Xia的筛选见算法5,其主要目的是根据现有真实评估过的解来删除一些希望渺茫的解,从而提高最终选出的解的质量.
其中,Xia为不存在活跃的邻居参考向量的解,即x∈Xia周围不存在真实评估的解.一方面,考虑到x 周围没有真实评估的解,需要尽量保留x 以探索其附近;另一方面,保留过差的x 对模型和种群都没有任何改善,因此,这里用种群P中所有的解来计算一个大体范围来筛选Xia.这里把d(Xr,z*)的最大值作为阈值dth筛选解Xia,删除d(x,z*)>dth的x.其中,d(Xr,z*)为集合Xr中每一个解到理想点z*的距离.
Xa为存在活跃的邻居参考向量的解,即x∈Xa周围存在真实评估的解.这里按照其邻居参考向量的最小相关解排序后的下四分位筛选Xa,阈值为
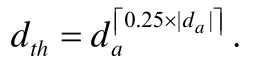
下四分位是描述整体样本前一半的平均指标,即保留与邻居参考向量上的最小相关解相比较好的x,这样对x 周围有较大的改善.
2.6 训练集更新
训练集A在每次迭代后都会进行更新,以保存多样性较好的解,以提高模型拟合的精度;同时,删除价值不大的解以减少建模时间.本文实验设置训练集A大小下限为11d-1,更新过程见算法6.
为了能够利用选择算子选出的解,步骤1 从解集X中选出一个d(x,z*)最小的解加入训练集A.步骤2 计算所有参考向量在种群P中的最小相关解集,并解加入训练集A.这样就可以得到多样性较好的的训练集,并且随着算法的迭代,样本会越来越靠近真实PF,从而帮助Kriging 模型较好地拟合真实PF 附近的空间.步骤4、步骤5从相关解最少的参考向量的相关解中选出最好的解加入训练集A.这是为了补充训练样本,防止训练样本过少而导致模型准确度下降.
算法6.训练集更新Update.

3 实 验
由于使用原昂贵问题评估需要花费大量的时间,若采用真实的昂贵问题,那么对比实验将会花费巨量的时间,实验的时间花费将会令人难以接受.因此,我们限制测试问题的真实评估次数来模拟解决昂贵多目标优化问题的场景,即测试问题只会被有限次地用于评估解.
本文实验通过在大规模2 目标和3 目标优化问题上的对比实验来证明DSAEA 的有效性.目前提出的基于Kriging 模型且性能较好的代理辅助进化算法有ParEGO,MOEA/D-EGO,K-RVEA,SMS-EGO.其中,由于SMS- EGO 需要计算S-metric来选解,所以运行速度非常慢,甚至需要几个小时才能运行一次.所以,我们使用另外几个算法作为对比算法.
3.1 测试问题集
实验选用ZDT[29]和DTLZ[30]测试问题作为基准测试问题.其中,选用ZDT1-4 和ZDT6 作为2 目标基准测试问题,选用DTLZ1-7 作为3 目标基准测试问题.
3.2 度量指标
实验选用反向迭代距离(inverted generational distance,简称IGD)[9]和超体积(hypervolume,简称HV)[31]作为度量指标.
(1) IGD 计算公式如下:

其中,P是对PF 均匀采样后得到的目标向量集合,P*是算法计算得到的目标向量集合,d(v,P)是一个目标向量v∈P*到P中最近的向量的距离.本文实验在PF 上均匀取10 000 个点作为参考点来计算IGD.
(2) HV 计算公式如下:

其中,P*是算法计算得到的目标向量集合,P′是P*中非支配解的集合,volume是计算向量到参考点的超体积.本文实验取点1.1××(max(f1),...,max(fm)),f1,...,fm∈PF 作为参考点来计算HV.
3.3 参数设置
(1) 一般设置
• 决策变量数量:ZDT 设置为12,DTLZ 设置为10;
• 目标变量数量:ZDT 设置为2,DTLZ 设置为3;
• 最大真实评估次数:ZDT 设置为200 次,DTLZ 设置为300 次;
• 初始采样数:利用LHS 方法采样11d-1 个解,ZDT 问题采样131 个解,DTLZ 问题采样109 个解;
• 交叉算子:模拟二进制交叉(simulated binary crossover)[27],设置概率为1.0,分布指数为20;
• 变异算子:多项式突变(polynomial mutation)[28],设置概率为1/d,分布指数为20;
• 候选解生成算子的最大评估次数:20×(11d-1)次模型评估;
• 参考向量数量:2 目标300 个(H=299),3 目标595 个(H=33).
• 独立运行次数:每个算法对每个测试问题独立运行30 次.
(2) 其他设置
DSAEA,MOEA/D-EGO 和K-RVEA 中每次迭代选出的解的数量设置为5,即μ=5.其他未说明的参数设置与其论文中的一致.
3.4 实验结果
IGD 结果见表1,HV 结果见表2,算法运行时间如表3.数字表示该指标的平均值,括号内的数字表示该指标的标准差,加粗表示在此测试问题上该项平均值为最优值.另外,我们使用秩和检验在显著性水平为0.05 下对30次独立运行结果进行分析.“+”表示此算法在此测试问题上与DSAEA 相比在该指标上表现更好,“-”表示此算法在此测试问题上与DSAEA 相比在该指标上表现更差,“≈”表示此算法在此测试问题上与DSAEA 相比在该指标上的表现区别不大.每个表格的最后一行还给出了在该指标上的+/-/≈结果的汇总.由于部分测试问题没有得到较好的收敛,甚至距离PF 非常远,如ZDT4,ZDT6,DTLZ1,DTLZ3,DTLZ6.在没有很好的收敛的情况下,对比多样性没有很大的意义,所以这里不讨论以上几个测试问题的HV 指标.

Table 1 Results of IGD 表1 反向迭代距离结果

Table 2 Results of HV表2 超体积结果

Table 3 Results of running time表3 运行时间结果
图2、图3 给出了DSAEA 与对比算法在ZDT,DTLZ 问题上的收敛曲线,横坐标为真实评估次数,纵坐标为IGD 指标.
对于ZDT 测试问题:
• IGD 和HV 结果表明:在实验设置一致的情况下,DSAEA 明显表现更好;
• 而收敛曲线表明:DSAEA 的收敛效果在大多数情况下要好于对比算法,只有在 ZDT1-3 问题上,DSAEA 的收敛效果在170 次真实评估前不如ParEGO.
由于ZDT1-3 问题较为简单,在最初阶段,搜索到比现有种群更优的解很容易,如果算法根据收敛性选解,则收敛速度会很快.但在靠近真实PF 的区域内,搜索到比现有种群更优的解相对不易,需要模型能够较好地拟合真实PF 附近的区域.不同于ParEGO,DSAEA 是基于多样性选解的,它更倾向于增加解集的多样性,使代理模型可以较好拟合目前种群最优解附近的区域.因此,DSAEA 的收敛曲线前30 次的收敛效果不如ParEGO,而之后的收敛效果要优于它.
对于DTLZ 测试问题,IGD,HV 结果和收敛曲线表明:在实验设置一致的情况下,DSAEA 在大多数的测试问题上明显表现更好;只有在DTLZ4 测试问题上,DSAEA 与K-RVEA 的效果相当;在DTLZ6 问题上,DSAEA 的表现不如MOEA/D-EGO.

Fig.2 Convergence curve of the algorithms on the ZDT problems图2 算法在ZDT 问题上的收敛曲线

Fig.3 Convergence curve of the algorithms on the DTLZ problems图3 算法在DTLZ 问题上的收敛曲线

Fig.3 Convergence curve of the algorithms on the DTLZ problems (Continued)图3 算法在DTLZ 问题上的收敛曲线(续)
图4 为DSAEA 和MOEA/D-EGO 的30 次独立运行中,最接近IGD 平均值的实验结果.可以看到:DSAEA大部分的解都集中在内部3 个参考向量附近,且有较多解向这真实PF 靠拢;而MOEA/D-EGO 大部分的解都集中在边界的3 个参考向量附近,其中只有几个非常好的解,其余大部分解距离真实PF 非常远.

Fig.4 On the DTLZ6 problem,the function evaluated solutions of DSAEA and MOEA/D-EGO are observed from different angles图4 在DTLZ6 测试问题上,从不同角度观察DSAEA 和MOEA/D-EGO 所有真实评估的解
在本实验中,DLTZ6 问题在决策空间内存在4 个不连续的PS区域,需要算法具有更高的探索能力.DSAEA是基于多样性的,在模型评估下,很好的解可能会被淘汰,转而保留增加多样性的解,这样可能会错过部分真实评估下很好的解.即便如此,DSAEA 的探索的大体趋势仍然要优于MOEA/D-EGO.
从收敛性和多样性上来看,DSAEA 要比目前较为流行的算法表现更好.
在运行时间方面,相对MOEA/D-EGO 和ParEGO,DSAEA 运行速度更快.相对K-RVEA,DSAEA 在大多数问题上运行速度相差不是太多,差异都在3%以下.其中,差异较大的问题为DTLZ1,DTLZ3,DTLZ2,DTLZ6,相比K-RVEA,DSAEA 在前两个问题上要慢12%左右,在后两个问题上要慢23%左右.对于以上几个问题,因为其PS分布在决策空间中范围较大,很容易搜索到不同方向的解,即在不同参考向量上的解,这就使训练集A的大小超过11d-1,增加了一定的建模时间.
从运行时间上来看,DSAEA 运行速度不亚于目前较为流行的算法.
由此可见,相比对比算法,DSAEA 在限制评估次数的情况下可以更加有效地解决实验选用的测试问题,主要分析有以下几点.
• 首先,DSAEA 引入参考向量的最小相关解来保持多样性.DSAEA 中,候选解生成算子不是按照支配关系迭代优化候选解,而是按照多样性,即会出现淘汰非支配解但保留支配解的情况.例如,x1支配x2,但x1所在参考向量已存在最小相关解且优于x1,而x2所在参考向量不存在相关解,则x1会被淘汰,而x2会被保留.值得一提的是:由于这里是采用模型评估,而模型评估总是存在一定的误差,所以在模型评估下的非支配解在真实评估下可能是支配解;反之亦然.此外,按照多样性保留解可以增加探索范围,避免陷入探索单一方向.因此,DSAEA 中候选解生成算子更有可能找到更多有希望的解,即,候选解生成算子迭代优化的目标是在模型评估下表现优秀的解以及未探索区域内的解;
• 其次,DSAEA 中的选择算子把解按照周围是否存在活跃参考向量进行划分筛选.一方面,DSAEA 会保留相比周围参考向量的最小相关解更好的解,以保留在真实评估下可能比现有解更好的解,从而提高当前解的收敛性;另一方面,DSAEA 会保留周围没有活跃参考向量的解,以对此未探索区域进行探索,从而提高当前解的多样性.在筛选后,DSAEA 对保留的解进行聚类,选出μ个代表解进行真实评估,进行批量的真实评估大大提升算法运行速度.这样,DSAEA 的选择算子对最终解的收敛性和多样性会有所帮助;
• 最后,由于测试问题决策变量数量较大,属于大规模问题,而模型精度有限,所以每次迭代后对训练集的更新是十分必要的.算法6 先对所有真实评估过的解,即种群P,计算其最小相关解加入训练集.若此时的训练集大小仍小于11d-1,则在剩下的解中按照参考向量上的解的密度继续选择,优先选择密度小的参考向量上的最小相关解加入训练集.这样做可以得到在目标空间内分布较为广泛且多样性较好的训练集,在此基础上,训练的模型会较好地拟合较大的范围,并且随着迭代次数的增加,训练集会更加靠近真实PF 区域,模型也就可以更好地拟合真实PF 附近区域.也就是说,随着迭代的进行,不仅进化算法会朝着真实PF 附近区域搜索,而且模型也会朝着真实PF 附近区域靠拢.
4 总 结
本文提出了基于多样性的代理辅助进化算法(DSAEA)来解决昂贵多目标优化问题.DSAEA 采用Kriging模型近似每个目标.候选解生成算子分配解到对应的参考向量来计算最小相关解集,以达到迭代优化候选解的目的.选择算子筛选出无活跃邻居参考向量的解,以及表现比大多数邻居参考向量的相关解更好的解.然后对筛选出的解K-means 聚类,从每个簇中选择一个最好的解进行真实评估.另外,DSAEA 使用一个大小下限为11d-1的训练集A作为代理模型的训练集,删除价值不大的样本以降低建模时间.实验部分选用大规模ZDT,DTLZ 测试问题,与目前流行的MOEA/D-EGO,K-RVEA 和ParEGO 算法进行对比实验.结果表明:DSAEA 在大多数选用的测试问题上,要比以上几个算法表现更好.因此,本文的方法是有效可行的.
在实验中,对于大规模问题来说,决策变量的数量设置较小,但仍有部分测试问题没有很好地收敛.当决策变量的量变得更大时,搜索和建模压力会随之上升,这对进化算法的选择和建模方法是一个巨大的挑战.另外,由于随着目标数量的增加,需要更多的解来近似表示PF,而昂贵问题中真实评估次数十分有限,所以如何用有限的点来有效地表示PF,也是一个严峻的挑战.

