斜拉桥斜拉索有限元模拟方法的比较
钱淼 朱运河 何东升
(中铁大桥勘测设计院集团有限公司,武汉 430050)
斜拉桥的跨度越大,几何非线性效应越明显。斜拉索的非线性主要由垂度效应引起。为了消除垂度效应,更准确地模拟斜拉索,文献[1]提出了索结构的等效模量法,文献[2]采用等效模量法考虑斜拉索垂度效应的杆单元来模拟斜拉索,文献[3]用悬链线单元模拟斜拉索。斜拉桥的非线性主要包括斜拉索的非线性、梁-柱几何非线性和大位移几何非线性[4-5]。若同时考虑这些非线性,则计算时间长,效率低。因此,需要解决的问题是:①选择兼顾精度和效率的斜拉索模拟方式;②斜拉索的非线性效应在斜拉桥非线性效应中所占比例。
模拟斜拉索的2种常用单元为:Ernst公式修正弹性模量的杆单元和悬链线单元。Ernst公式修正弹性模量的杆单元可以采用线性的切线模量法,也可以采用非线性的割线模量法,但后者计算精度和效率都低于悬链线单元,所以本文只研究切线模量法。切线模量法的原理:斜拉索的刚度采用上一个荷载步结束时的刚度,且在一次加载计算过程中保持不变。悬链线单元是非线性单元,是模拟斜拉索的最准确方式,但需要迭代计算。因此,与杆单元相比,悬链线单元计算精度更高,但计算效率低。
本文对浩吉铁路洞庭湖特大桥主桥采用2种单元模拟斜拉索,通过对比2种单元的内力和刚度,研究Ernst公式修正弹性模量的杆单元在什么状态下更接近悬链线单元,并对比分析其在不同工况下的计算精度和计算效率。
1 斜拉索模拟方法对比
1.1 内力
杆单元的内力Tb由2部分组成:①单元刚度矩阵乘以节点位移获得的内力T;②自重G产生的内力在杆单元两端均分。即Tb等于G/2与T的矢量和,在水平和竖直向的分力为Hb和Vb(图1(a))。悬链线单元的内力Ta根据平衡状态计算得到[3,6],其在水平和竖直向的分力为Ha和Va(图1(b))。实际的斜拉索形状是悬链线,悬链线单元的内力方向在悬链线的切向,但杆单元的内力方向并不在悬链线的切向上。2种单元的内力存在夹角,即张拉力角度。

图1 斜拉索模拟单元的内力
以一斜拉索为例,其面积为0.001 4 m2,弹性模量E为1.9×105MPa,重度γ为78 kN/m3。杆单元张拉力Tb和悬链线单元张拉力Ta的大小一样,方向不一样。应力、弦长、倾斜角度α与张拉力角度的关系见图2。可知:斜拉索应力越大,斜拉索弦长越短,张拉力角度越小,则采用Ernst公式修正弹性模量的杆单元模拟斜拉索越准确;α=45°时,张拉力角度最大。

图2 应力、弦长、倾斜角度与张拉力角度的关系
1.2 刚度
斜拉索IJ的几何位置参数见图3。其中,l为斜拉索水平投影长度;s为斜拉索弦长,l=s·cosα。

图3 斜拉索几何位置参数
Ernst公式修正杆单元的弹性模量Etan计算公式为

式中:σ1为斜拉索应力。
根据斜拉索单元坐标系(参见图3)可知,斜拉索单元的刚度K矩阵分为4块,即

由于KII=KJJ,KIJ=KJI=-KII,所以研究2种单元的刚度矩阵只须对比KII。参考文献[6-8]可获得悬链线单元的刚度,即

kxy,kyx,kzy,kyz均为 0,斜拉索IJ连线方向的刚度kL是主要刚度,通过坐标转化将kxx,kzx,kxz,kzz转换得到kL,可对比2种单元的刚度差异。
α=25°,s=500 m时,不同斜拉索应力下2种单元的刚度见表1。其中,相差百分比=(杆单元刚度-悬链线单元刚度)/杆单元刚度。由表1可知:2种单元的刚度相差不大;斜拉索应力越大,单元刚度越大;斜拉索应力从100 MPa增加到200 MPa时,单元刚度增加了5倍,斜拉索应力从400 MPa增加到500 MPa时,单元刚度只增加了13%。这说明斜拉索应力越大,施工过程中斜拉索应力变化越小,采用Ernst公式修正弹性模量的杆单元模拟斜拉索越准确。
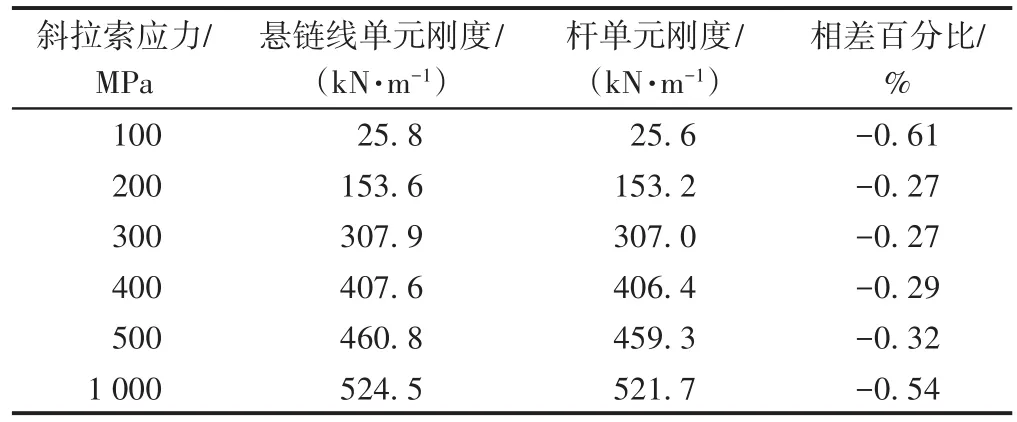
表1 不同斜拉索应力下2种单元的刚度
α=25°,σ1=200 MPa时,不同弦长下2种单元的刚度见表2。可知:2种单元的刚度相差不大;斜拉索弦长越大,2种单元的刚度越小。

表2 不同弦长下2种单元的刚度
s=500 m,σ1=200 MPa时,不同倾斜角度下2种单元的刚度见表3。可知:2种单元的刚度相差不大;斜拉索越接近竖直,其刚度越大。

表3 不同倾斜角度下2种单元的刚度
综上可知:2种单元的刚度相差不大;斜拉索应力越大,弦长越短,施工过程中斜拉索应力变化越小,则采用Ernst公式修正弹性模量的杆单元模拟斜拉索越准确。
2 工程实例分析
2.1 工程概况
浩吉铁路洞庭湖特大桥主桥为三塔双索面钢箱钢桁结合梁斜拉桥,首次采用三塔斜拉桥和箱桁组合结构,是浩吉铁路煤运通道的关键控制性工程。该桥全长1 290.24 m,桥跨布置见图4。

图4 洞庭湖特大桥主桥桥跨布置(单位:m)
主梁为钢箱钢桁结合梁结构,主桁采用内倾布置,上弦和下弦中心距分别为12.0,14.0 m。全联桁架为不带竖杆的华伦式桁架,桁高12.0 m,节间长14.0 m,斜杆立面倾角59.744°。全桥共92个节间,以4#塔对称布置。钢梁断面见图5。
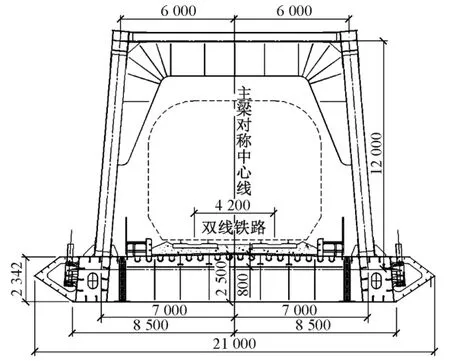
图5 钢梁断面(单位:mm)
施工步骤:先悬臂施工钢箱,钢箱合龙后再施工钢桁。施工钢箱时斜拉索索力比较低,斜拉索的非线性效应较明显。
2.2 计算模型
结构静力计算时,采用中铁大桥勘测设计院集团有限公司自编空间有限元程序3D Bridge V6建立全桥空间有限元模型。塔、梁均采用梁单元模拟,斜拉索根据不同的计算方法采用Ernst公式修正弹性模量的杆单元和悬链线单元。全桥共划分2 000个梁单元,24个支承单元,1 667个节点。
一个典型的悬拼循环过程为:斜拉索张拉→吊机起吊下一片梁段→梁段安装好后吊机前移至梁前端→张拉下一对斜拉索。
2.3 计算方法
为了对比Ernst公式修正弹性模量的杆单元和悬链线单元的计算精度和计算效率,研究斜拉索的非线性在斜拉桥非线性效应中占的比例,采用3种方法计算主梁位移。
方法1:用Ernst公式修正弹性模量的杆单元模拟斜拉索。此方法未完全解决斜拉索的非线性问题且没有解决其他几何非线性问题,精度最低。
方法2:用悬链线单元模拟斜拉索,且不考虑其他几何非线性的影响。此方法只解决了斜拉索的非线性问题,精度高于方法1。
方法3:用悬链线单元模拟斜拉索,且考虑其他几何非线性的影响。此方法解决了所有几何非线性问题,精度最高。
如果方法1与方法3的计算结果相差大,表明不适合采用Ernst公式修正弹性模量的杆单元模拟斜拉索。如果方法2与方法3的计算结果接近,而与方法1的计算结果相差大,表明斜拉索的非线性效应在斜拉桥几何非线性效应中占主导地位。
2.4 计算结果
3种计算方法的桥梁结构、边界条件和荷载条件完全相同。选取3种工况对3种计算方法的结果进行对比分析:①工况1(斜拉索被动加载),E30E31箱梁段安装,即中跨箱梁合龙前安装最后一段箱梁;②工况2(斜拉索被动卸载),挂设张拉13#索,即中跨箱梁合龙前挂设最后一根斜拉索;③工况3(成桥),成桥后在跨中施加300 kN的竖向荷载。
2.4.1 工况1
E30E31箱梁段安装前后,跨中最长索的应力从236 MPa增加到298 MPa,刚度增加了1.5倍左右。E30E31箱梁段安装前后钢梁线形变化对比见表4。可知:①方法1的计算结果比其他2种方法的计算结果大10%左右,表明此工况不适合采用方法1。②方法2和方法3的计算结果相差不大。方法1—方法3的计算时间分别为7,9,13 s。
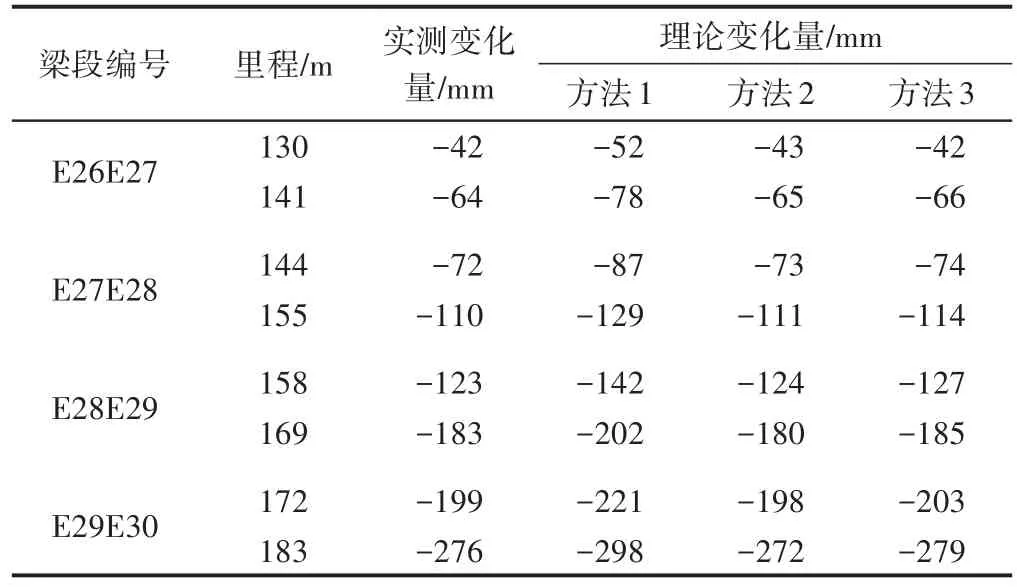
表4 E30E31箱梁段安装前后钢梁线形变化对比
2.4.2 工况2
挂设13#斜拉索时已经安装的斜拉索被动卸载,造成应力减小,中跨第2长索的应力从273 MPa减小到113 MPa,刚度减小50%左右。张拉13#索前后钢梁线形变化对比见表5。可知:①方法1的计算结果比其他2种方法的计算结果小10%左右,表明此工况不适合采用方法1;②方法2和方法3的计算结果相差不大。方法1—方法3的计算时间分别为6,8,12 s。
2.4.3 工况3
成桥后在跨中加300 kN竖向荷载,方法1—方法3计算的跨中竖向位移分别为-6.31,-6.59,-6.68 mm,计算时间分别为8,10,13 s。成桥时斜拉索应力较大,竖向荷载对索应力的改变量不超过2 MPa,且塔直梁平,所以斜拉索的非线性效应和其他几何非线性效应都不大。
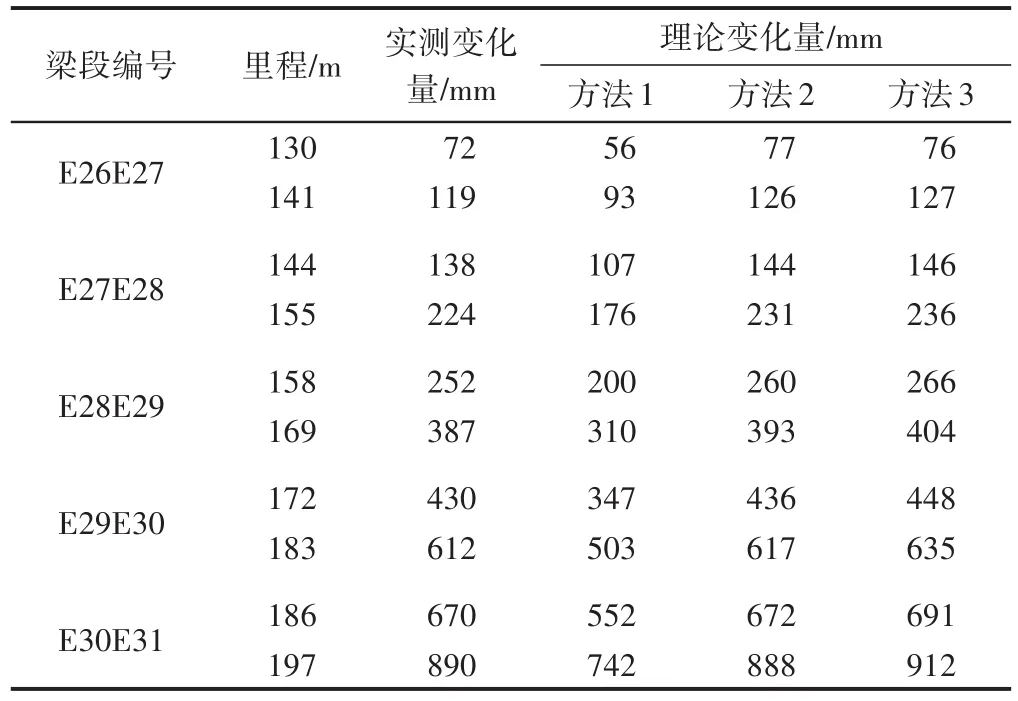
表5 张拉13#索前后钢梁线形变化对比
综上可知:工况1和工况2不适合采用方法1;斜拉索的非线性在斜拉桥非线性效应中占主导地位;工况3采用方法1能满足精度要求且计算效率最高。
3 结论
1)斜拉索应力越大,弦长越短,施工过程中斜拉索应力变化越小,则采用Ernst公式修正弹性模量的杆单元模拟斜拉索越准确。
2)施工过程中,斜拉索应力过小或变化较大时,斜拉索的刚度会产生较大的变化,采用Ernst公式修正弹性模量的杆单元误差较大,应采用悬链线单元。
3)斜拉桥成桥状态,塔直梁平且斜拉索应力较大,非线性效应不明显,采用Ernst公式修正弹性模量的杆单元能够得到精度较高的结果。
4)斜拉索的非线性在斜拉桥非线性效应中占主导地位,悬链线单元比Ernst公式修正弹性模量的杆单元的精度更高,但效率略低。

