混合图的埃尔米特-ABC能量

孙 洁，邵燕灵

(中北大学 理学院，山西 太原 030051)

0 引 言

本文考虑的图均为简单图.设G为一个具有顶点集V(G)={v1,v2,…,vn}和边集E(G)的无向图，如果图M是对无向图G的某些边加上方向后而获得的，则称M为混合图，称无向图G为M的基本图，记为Mu.混合图M的顶点集V(M)与其基本图的顶点集V(Mu)相同，边集E(M)是无向边的集合E0与有向边的集合E1的并集.

设M是顶点集为V(M)={v1,v2,…,vn}和边集为E(M)的混合图，用vkvl(或vk↔vl)表示M中连接两个顶点vk和vl的无向边，用(vk,vl)(或vk→vl)表示从vk到vl的有向边(或弧).用dk=d(vk)=dG(vk)表示无向图G中顶点vk的度.对于混合图M，用dk=d(vk)=dMu(vk)表示其基础图Mu中顶点vk的度.

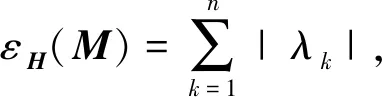
(1)

图G的ABC指数定义为[6]

(2)

其相关的研究见文献[7-9].

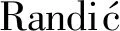
如果在混合图M的每一条边和弧上加上ABC权，就可以得到一个新的加权埃尔米特邻接矩阵.下面给出具体定义.设M是顶点集为V(M)={v1,v2,…,vn}的一个混合图，定义M的埃尔米特-ABC矩阵为n阶矩阵ABCH(M)=((wh)kl)，其中

(3)

本文定义了混合图的埃尔米特-ABC矩阵ABCH(M)，给出了混合图的埃尔米特-ABC能量的一些界，并刻画了有向图D1和D2的埃尔米特-ABC能量与混合图D1∨D2的埃尔米特-ABC能量之间的关系，其中D1∨D2是在有向图D1的每个顶点与有向图D2的所有顶点之间各添加一条无向边而得到的混合图.

1 预备知识

引理1[8]设G为无孤立点的n≥2阶无向图，Δ(G)与δ(G)分别为G的最大度与最小度，则

(4)

两边等号成立当且仅当G为正则图.

引理2 设M为n阶混合图，Mn为M的基本图，η1≥η2≥…≥ηn为ABCH(M)的特征值，则

2(n-2R-1(Mu)),

(5)

证明因为

(6)

故结论成立.证毕.

2 混合图的埃尔米特-ABC能量的界

证明设η1≥η2≥…≥ηn为ABCH(M)的特征值，则存在一个n阶酉矩阵U，使得

U*ABCH(M)U=U*ABCH(M)*U=

diag{η1,η2,…,ηn}.

(7)

定理2 设M为n≥3阶混合图，Mu为M的基本图，η1≥η2≥…≥ηn为ABCH(M)的特征值，p=|detABCH(M)|，则

(8)

(9)

另一方面，

(10)

由算术几何平均不等式，得到

(11)

因此

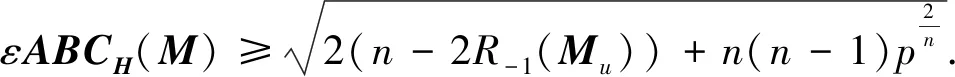
(12)

由柯西-施瓦茨不等式和算术几何平均不等式可知，式(12)等号成立当且仅当|η1|=|η2|=…=|ηn|，再由定理1知，结论成立.证毕.

推论1 设M为n阶混合图，M的基本图Mu为k正则图，且Mu的边数为m，η1≥η2≥…≥ηn为ABCH(M)的特征值，p=|detABCH(M)|，则

(13)

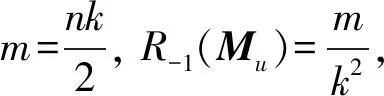
定理3 设M为n≥3阶的无孤立点的混合图，且Mu为M的基本图，η1≥η2≥…≥ηn为ABCH(M)的特征值，Δ与δ分别表示Mu的最大度与最小度，则

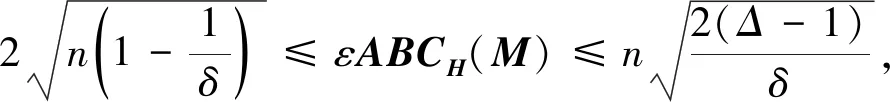
(14)

上界等式成立当且仅当Mu为正则图且|η1|=|η2|=…=|ηn|；下界等式成立当且仅当Mu为正则图且|η1|=|ηn|≠0,ηj=0,j=2,…,n-1.

证明由柯西-施瓦兹不等式及引理2，

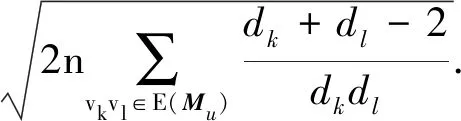
(15)

(16)

再由引理1，

(17)

由上面证明过程并结合引理1，可知上界等式成立当且仅当Mu为正则图且|η1|=|η2|=…=|ηn|.

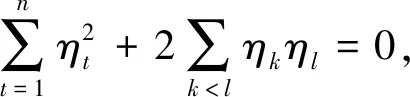
(18)

4(n-2R-1(Mu)),

(19)

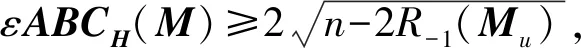
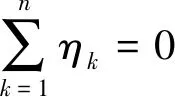
3 一类混合图的埃尔米特-ABC能量

设D1和D2为两个有向图，图D1∨D2是在D1的每个顶点与D2的所有顶点之间各添加一条无向边而得到的混合图.用odD(u)表示有向图D中顶点u的出度(即D中以顶点u为始点的边数)，idD(u)表示有向图D中顶点u的入度(即D中以顶点u为终点的边数).本节刻画了有向图D1和D2的埃尔米特-ABC能量与混合图D1∨D2的埃尔米特-ABC能量之间的关系.

φABC(D1∨D2,λ)=

(20)

(21)

则混合图D1∨D2的埃尔米特-ABC矩阵的特征多项式为

φABCH(D1∨D2∶λ)=

由于对任意顶点u∈V(Dj)都有odDj(u)=idDj(u)，故

(23)

对式(22)作如下变换：从第n1+2行到第n1+n2行，每一行都减去第n1+1行，再从第n1+2 列到第n1+n2列，每一列都加到第n1+1列上，然后从第2行到第n1行，每一行都减去第1行，再从第2列到第n1列，每一列都加到第1列上，并利用式(23)得

φABCH(D1∨D2∶λ)=

(λ2-n1n2a2)|A||B|,

(24)

其中

将|A|升阶为n1阶行列式

|A|=

(25)

从第2列到第n1列，每一列都乘-1加到第1列上，再从第2行到第n1行，每一行都加上第1行，可得

|A|=

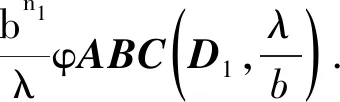
(26)

εABCH(D1∨D2)=bεABCH(D1)+

(27)

证明由定理4知，

λ2φABCH(D1∨D2∶λ)=

(28)